
Des
Apollonius von Perga
sieben Bücher über Kegelschnitte
nebst dem durch Halley wieder hergestellten
achten Buche.
Deutsch bearbeitet von
B. Balsam.
Dabei ein Anhang, enthaltend:
Die auf die Geometrie der Kegelschnitte bezüglichen Sätze aus Newtons "philosophiæ naturalii principia mathematica."
Berlin, 1861.
Verlag von Georg Reimer.
Erste Erklärungen.
Wenn von einem Punkte nach dem Umfang eines Kreises, der nicht in derselben Ebene mit dem Punkt liegt, eine gerade Linie gezogen und nach beiden Seiten verlängert wird, und, indem der Punkt fest bleibt, im Umfang des Kreises herumgeführt wird, bis sie wieder an den Ort zurückkehrt, von wo sie sich zu bewegen anfing, so nenne ich die von der geraden Linie beschriebene Oberfläche, welche aus zwei Theilen besteht, die am Scheitel unter sich zusammenhängen, und welche beide ins Unendliche fortgehen, da ja die erzeugende gerade Linie ins Unendliche verlängert ist,
- Die Kegeloberfläche.
- Den Scheitel derselben den festen Punkt.
- Die Achse die gerade Linie, welche durch den festen Punkt und den Mittelpunkt des Kreises gezogen wird.
- Kegel nenne ich den Körper, der von dem Kreis und dem Theil der Kegeloberfläche, der zwischen dem Kreis und dem Scheitel liegt, begrenzt wird.
- Scheitel des Kegels den Punkt, der auch Scheitel der Kegelfläche ist.
- Achse die Linie, welche vom Scheitel nach dem Mittelpunkt des Kreises gezogen wird.
- Grundfläche den Kreis selbst.
- Gerade Kegel nenne ich diejenigen, deren Achse senkrecht auf der Grundfläche steht.
- Schiefe Kegel, deren Achse nicht senkrecht auf der Grundfläche steht.
- Von jeder in einer Ebene befindlichen krummen Linie nenne ich einen Durchmesser eine solche Gerade, welche, von der krummen Linie ausgehend, alle mit einer gewissen Linie parallelen Sehnen, die in derselben gezogen werden, halbiert.
- Scheitel den Endpunkt des Durchmessers, der sich in der krummen Linie befindet.
- Jede der erwähnten parallelen Linien eine zu dem Durchmesser gehörige Ordinate.
- Auf ähnliche Weise nenne ich auch, wenn zwei in einer Ebene liegende krumme Linien gegeben sind, einen Querdurchmesser eine solche Linie, die alle in jeder derselben einer gewissen Geraden parallel gezogenen Sehnen halbiert.
- Scheitel der Linien nenne ich die Endpunkte der Durchmesser auf ihnen.
- Längsdurchmesser zweier solcher Kurven nenne ich eine solche Gerade, die, zwischen beiden liegend, alle mit einer gewissen Geraden parallelen von beiden Kurven begrenzten Linien halbiert.
- Konjugierte Durchmesser einer und zweier Kurven nenne ich zwei solche Linien, von denen jede ein Durchmesser ist, und die der andern parallel gezogenen Linien halbiert.
- Achse einer und zweier Kurven nenne ich eine solche Linie, die ein Durchmesser ist, und senkrecht auf den von ihr halbierten Linien steht.
- Konjugierte Achsen einer oder zweier Kurven nenne ich gerade Linien, die konjugierte Durchmesser sind, und senkrecht auf einander stehen.
Lehrsatz 1. Die geraden Linien, welche vom Scheitel, einer Kegeloberfläche nach solchen Punkten, die auf ihr liegen, gezogen werden, befinden ich ganz in ihr.
 Sei eine Kegelfläche mit dem Scheitel A gegeben und in ihr ein Punkt B angenommen, sei ferner die gerade Linie ACB gezogen; so wird behauptet, dass ACB auf der Oberfläche liegt. Angenommen, sie liege nicht darin; so sei DE die gerade Linie, die die Fläche erzeugt, FE der Kreis, durch den sie geführt wird. Wenn nun A fest bleibt und die gerade Linie DE durch den Kreis EF herumgeführt wird, muss sie einmal den Punkt B treffen. Dann hätten also zwei gerade Linien die selben zwei Endpunkte, was unmöglich ist. Also liegt die von A nach B gezogene Linie nicht außerhalb der Kegelfläche und folglich in derselben.
Sei eine Kegelfläche mit dem Scheitel A gegeben und in ihr ein Punkt B angenommen, sei ferner die gerade Linie ACB gezogen; so wird behauptet, dass ACB auf der Oberfläche liegt. Angenommen, sie liege nicht darin; so sei DE die gerade Linie, die die Fläche erzeugt, FE der Kreis, durch den sie geführt wird. Wenn nun A fest bleibt und die gerade Linie DE durch den Kreis EF herumgeführt wird, muss sie einmal den Punkt B treffen. Dann hätten also zwei gerade Linien die selben zwei Endpunkte, was unmöglich ist. Also liegt die von A nach B gezogene Linie nicht außerhalb der Kegelfläche und folglich in derselben.
Lehrsatz 2. Wenn in einer der beiden am Scheitel zusammenstoßenden Flächen zwei Punkte angenommen und durch eine gerade Linie verbunden werden, diese aber weder selbst, noch in ihrer Verlängerung den Scheitel trifft, so liegt sie innerhalb der Oberfläche, ihre Verlängerung aber ausserhalb derselben.
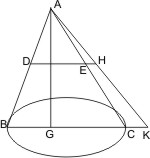 Sei eine Kegelfläche mit dem Scheitel A gegeben, der Kreis, um den die erzeugende Linie herumgeführt wird, sei BC, und in einer der beiden am Scheitel zusammenstossenden Flächen seien zwei Punkte D und E angenommen und durch eine gerade Linie verbunden, so behaupte ich, dass DE innerhalb der Fläche liegt, ihre Verlängerung aber ausserhalb. Man ziehe AD, AE und verlängere sie, bis sie den Grundkreis in den Punkten B,C schneiden, und ziehe BC, so wird BC innerhalb des Kreises, also auch innerhalb der Kegelfläche liegen. Man nehme nun in DE einen beliebigen Punkt F an, verbinde AF und verlängere es, bis es BC im Punkte G trifft. Weil nun G innerhalb der Kegelfläche liegt, wird auch AG und also auch der Punkt F innerhalb derselben liegen müssen; und auf die nämliche Weise wird gezeigt werden können, dass alle an dem Punkte von DE innerhalb der Kegelfläche liegen; daher liegt also DE selbst innerhalb. Man verlängere nun DE zum Punkte H, so wird behauptet, dass EH ausserhalb der Kegelfläche sich befinde. Sei, wenn es möglich ist, ein Punkt H derselben nicht ausserhalb, und werde AH gezogen, so muss dieselbe verlängert, entweder den Umfang des Kreises oder innerhalb desselben die Ebene treffen; was nicht geschehen kann, denn sie trifft die verlängerte BC hier im Punkte K. Also liegt EH ausserhalb der Kegelfläche. Die Linie DE selbst nun liegt also innerhalb, ihre Verlängerung ausserhalb der Kegelfläche.
Sei eine Kegelfläche mit dem Scheitel A gegeben, der Kreis, um den die erzeugende Linie herumgeführt wird, sei BC, und in einer der beiden am Scheitel zusammenstossenden Flächen seien zwei Punkte D und E angenommen und durch eine gerade Linie verbunden, so behaupte ich, dass DE innerhalb der Fläche liegt, ihre Verlängerung aber ausserhalb. Man ziehe AD, AE und verlängere sie, bis sie den Grundkreis in den Punkten B,C schneiden, und ziehe BC, so wird BC innerhalb des Kreises, also auch innerhalb der Kegelfläche liegen. Man nehme nun in DE einen beliebigen Punkt F an, verbinde AF und verlängere es, bis es BC im Punkte G trifft. Weil nun G innerhalb der Kegelfläche liegt, wird auch AG und also auch der Punkt F innerhalb derselben liegen müssen; und auf die nämliche Weise wird gezeigt werden können, dass alle an dem Punkte von DE innerhalb der Kegelfläche liegen; daher liegt also DE selbst innerhalb. Man verlängere nun DE zum Punkte H, so wird behauptet, dass EH ausserhalb der Kegelfläche sich befinde. Sei, wenn es möglich ist, ein Punkt H derselben nicht ausserhalb, und werde AH gezogen, so muss dieselbe verlängert, entweder den Umfang des Kreises oder innerhalb desselben die Ebene treffen; was nicht geschehen kann, denn sie trifft die verlängerte BC hier im Punkte K. Also liegt EH ausserhalb der Kegelfläche. Die Linie DE selbst nun liegt also innerhalb, ihre Verlängerung ausserhalb der Kegelfläche.
Lehrsatz 3. Wenn ein Kegel von einer durch den Scheitel gelegten Ebene geschnitten wird, so ist der Schnitt ein Dreieck.
Sei ein Kegel mit dem Scheitel A gegeben, die Grundfläche der Kreis BC, und werde derselbe von einer Ebene durch den Scheitel A geschnitten, welche in der Kegelfläche die Linien AB, AC bildet, und in der Grundfläche die gerade Linie BC; so wird behauptet, dass ABC ein Dreieck sei. Die gerade Linie zwischen A und B muss aber nach § 1. in der Kegelfläche und zugleich auch in der schneidenden Ebene liegen nach der Erklärung der Ebene; also ist sie der Durchschnitt der beiden Flächen, auf dieselbe Weise AC, und BC ist eine gerade Linie als Durchschnitt zweier Ebenen; also ist ABC ein Dreieck. Wenn also ein Kegel von einer Ebene durch den Scheitel geschnitten wird, so ist der Durchschnitt ein Dreieck.
Lehrsatz 4. Wenn eine der beiden Flächen, die am Scheitel zusammenstoßen, durch eine der Grundfläche parallele Ebene geschnitten wird, so wird der Theil der Ebene, der innerhalb der Kegelfläche liegt, ein Kreis sein, dessen Mittelpunkt in der Achse ist; der Körper aber, der von diesem Kreise und demjenigen Theil der Kegelfläche begrenzt wird, welcher zwischen der schneidenden Ebene und dem Scheitel liegt, ist ein Kegel.
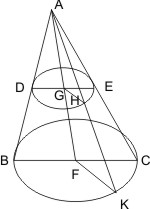 Es sei eine Kegelfläche mit dem Scheitel A und dem Grundkreis BC gegeben, und es werde dieselbe durch eine dem Kreis BC parallele Ebene geschnitten, welche die Kegelfläche in der Linie DE durchschneidet; so wird behauptet, dass DE ein Kreis sei, der seinen Mittelpunkt in der Achse bat. Es sei der Mittelpunkt F des Kreises BC genommen und von F nach A gezogen, welche Linie der schneidenden Ebene in G begegne, ferner durch AF eine Ebene gelegt, welche den Grundkreis in der geraden Linie BC, die schneidende Ebene in der geraden DE trifft; endlich nehme man in der Linie DE auf der Kegelfläche einen beliebigen Punkt H, ziehe AH, verlängere es, bis es dem Grundkreis in K begegnet und ziehe GH und FK. Da nun die Ebenen DHE und BKC parallel sind, werden auch die in denselben befindlichen Durchschnittslinien DE und BC, sowie GH und FK parallel sein, weshalb
Es sei eine Kegelfläche mit dem Scheitel A und dem Grundkreis BC gegeben, und es werde dieselbe durch eine dem Kreis BC parallele Ebene geschnitten, welche die Kegelfläche in der Linie DE durchschneidet; so wird behauptet, dass DE ein Kreis sei, der seinen Mittelpunkt in der Achse bat. Es sei der Mittelpunkt F des Kreises BC genommen und von F nach A gezogen, welche Linie der schneidenden Ebene in G begegne, ferner durch AF eine Ebene gelegt, welche den Grundkreis in der geraden Linie BC, die schneidende Ebene in der geraden DE trifft; endlich nehme man in der Linie DE auf der Kegelfläche einen beliebigen Punkt H, ziehe AH, verlängere es, bis es dem Grundkreis in K begegnet und ziehe GH und FK. Da nun die Ebenen DHE und BKC parallel sind, werden auch die in denselben befindlichen Durchschnittslinien DE und BC, sowie GH und FK parallel sein, weshalb
- FA : GA = FB : GD
- FA : GA = FK : GH
- FA : GA = FC : GE
Da nun dasselbe von allen in DE auf der Kegelfläche angenommenen Punkten gezeigt werden kann, so ist bewiesen, dass die Durchschnittslinie DE ein Kreis ist und ihren Mittelpunkt in der Achse AF hat.
Es erhellt ausserdem aus der Erklärung, dass der von dem Kreis DE und demjenigen Theil der Kegelfläche, der zwischen diesem Kreis und dem Scheitel A liegt, eingeschlossene Körper ein Kegel ist, und es ist zugleich gezeigt, dass der gemeinschaftliche Durchschnitt der schneidenden Ebene und des durch die Achse gelegten Dreiecks ein Durchmesser des in der schneidenden Ebene befindlichen Kreises ist.
Lehrsatz 5. Wenn ein schiefer Kegel durch eine Ebene geschnitten wird, die durch die Achse geht und senkrecht auf der Grundfläche steht und dann von einer zweiten, die senkrecht auf der ersten steht und von dem durch die erste gebildeten Achsendreieck ein ähnliches Dreieck dergestalt abschneidet, dass die Winkel an der Grundlinie verwechselt liegen, so ist der Durchschnitt der zweiten Ebene mit dem Kegel ein Kreis. Man nennt diesen Kreis einen Wechselschnitt.
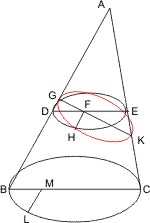 Es sei ein schiefer Kegel mit dem Scheitel A und der Grundfläche BC gegeben; derselbe werde durch eine auf der Grundfläche senkrechte und durch die Achse gehende Ebene geschnitten, welche das Achsendreieck ABC giebt, ferner durch eine zweite auf der Ebene ABC senkrechte Ebene, welche von dem Dreieck ABC nach dem Scheitel A zu ein ähnliches Dreieck AGK abschneidet, dessen Winkel an der Grundlinie aber verwechselt liegen, so nämlich, dass der ∠AKG = ∠ABC ist, und es sei der Durchschnitt dieser zweiten Ebene mit der Kegelfläche die Linie GHK; so wird behauptet, dass GHK ein Kreis ist.
Es sei ein schiefer Kegel mit dem Scheitel A und der Grundfläche BC gegeben; derselbe werde durch eine auf der Grundfläche senkrechte und durch die Achse gehende Ebene geschnitten, welche das Achsendreieck ABC giebt, ferner durch eine zweite auf der Ebene ABC senkrechte Ebene, welche von dem Dreieck ABC nach dem Scheitel A zu ein ähnliches Dreieck AGK abschneidet, dessen Winkel an der Grundlinie aber verwechselt liegen, so nämlich, dass der ∠AKG = ∠ABC ist, und es sei der Durchschnitt dieser zweiten Ebene mit der Kegelfläche die Linie GHK; so wird behauptet, dass GHK ein Kreis ist.
Man nehme in den Linien GHK, BC zwei beliebige Punkte H, L an und fälle von ihnen auf die zuerst gelegte Ebene des Dreiecks ABC Lothe, so müssen diese, weil die Ebenen lotbrecht stehen, die Durchschnittslinien BC,GK der beiden Ebenen BC und GHK mit ABC treffen. Seien also diese Lothe HF und LM. Es werde nun durch F mit BC eine Parallele DFE gezogen, so wird die durch FH und DE gelegte Ebene mit der Grundfläche parallel und also ihr Schnitt DHE in dem Kegel ein Kreis sein, dessen Durchmesser DE ist, also ist:- HF2 = DF · FE.
Da ferner nach Annahme ∠AKG = ∠ABC, und ∠ABC = ∠ADE ist, ist das ΔEFK ~ ΔGFD, und also muss EF : GF = FK : DF oder - EF · DF = GF · FK
Da nun dasselbe für alle Punkte des Schnitts GHK bewiesen werden kann, ist gezeigt, dass dieser ein Kreis, und dass sein Durchmesser GK ist.- HF2 = DF · FE.
Lehrsatz 6. Wenn ein Kegel von einer durch die Achse gehenden Ebene geschnitten und von einem Punkt der Kegelfläche, der nicht in dieser schneidenden Ebene liegt, eine Parallele mit einem auf der Grundlinie des entstandenen Achsendreiecks in der Grundfläche errichteten Loth gezogen wird, so trifft diese Parallele die Ebene des Achsendreiecks, und wird, über diesen Durchschnitt hinaus bis wieder an die Kegelfläche verlängert, von derselben halbiert.
Sei ein Kegel mit dem Scheitel A und dem Grundkreis BC gegeben und werde derselbe von einer durch die Achse gelegten Ebene geschnitten, so dass das Achsendreieck ABC entsteht; wird ferner von einem beliebigen Punkt M im Umfang des Grundkreises die Linie MN senkrecht gegen BC, und von einem beliebigen in der Kegelfläche angenommenen Punkt D die Linie DE parallel mit MN gezogen, so wird behauptet, dass DE der Ebene des Achsendreiecks ABC begegnet und, nach der andern Seite bis zu ihrem Durchschnitt mit der Kegelfläche verlängert, durch die Ebene des Dreiecks ABC halbiert werde.
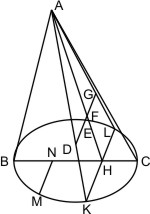 Man ziehe AD, verlängere es, bis es dem Umfang des Grundkreises in K begegnet, und fälle von K auf BC das Loth KHL, so wird KH parallel MN, also auch parallel DE sein. Man ziehe nun AH; da nun in dem Dreieck AHK DE parallel mit HK gezogen ist, muss es, verlängert, AH treffen und da AH in der Ebene ABC liegt, ist bewiesen; dass DE dieser Ebene begegnet; sei nun der Durchschnittspunkt F, und werde DF verlängert, bis es der Kegelfläche in G begegnet, so ist noch zu zeigen, dass DF = FG ist. Da aber die Punkte G und L sowohl in der Kegelfläche, als in der Ebene des Dreiecks AKH liegen, welche durch den Scheitel A des Kegels geht, müssen sie sich mit diesem in gerader Linie befinden. Nun ist aber in dem Dreieck AKL DG parallel der Basis gezogen, also KH : HL = DF : FG und da KH = HL, ist auch DF = FG. q. e. d.
Man ziehe AD, verlängere es, bis es dem Umfang des Grundkreises in K begegnet, und fälle von K auf BC das Loth KHL, so wird KH parallel MN, also auch parallel DE sein. Man ziehe nun AH; da nun in dem Dreieck AHK DE parallel mit HK gezogen ist, muss es, verlängert, AH treffen und da AH in der Ebene ABC liegt, ist bewiesen; dass DE dieser Ebene begegnet; sei nun der Durchschnittspunkt F, und werde DF verlängert, bis es der Kegelfläche in G begegnet, so ist noch zu zeigen, dass DF = FG ist. Da aber die Punkte G und L sowohl in der Kegelfläche, als in der Ebene des Dreiecks AKH liegen, welche durch den Scheitel A des Kegels geht, müssen sie sich mit diesem in gerader Linie befinden. Nun ist aber in dem Dreieck AKL DG parallel der Basis gezogen, also KH : HL = DF : FG und da KH = HL, ist auch DF = FG. q. e. d.
Lehrsatz 7. Wenn ein Kegel von einer durch die Achse gelegten Ebene und zugleich von einer andern Ebene, deren Durchschnittslinie mit der Grundfläche senkrecht auf der Grundlinie des durch die erste Ebene entstandenen Achsendreiecks oder ihrer Verlängerung steht, geschnitten wird, so werden diejenigen Linien, welche vom Umfang des durch die zweite Ebene entstandenen Kegelschnitts, parallel der in der Grundfläche befindlichen Durchschnittslinie gezogen werden, die gemeinschaftliche Durchschnittslinie der beiden gelegten Ebenen treffen, und auf der andern Seite bis zur Kegelfläche verlängert, von dieser Durchschnittslinie halbiert werden. Wenn der Kegel gerade ist, so steht die in der Grundfläche befindliche Linie senkrecht auf der Durchschnittslinie der schneidenden Ebene und des Achsendreiecks, ist aber der Kegel schief, so ist das nur dann der Fall, wenn die Ebene des Achsendreiecks senkrecht auf der Grundfläche des Kegels steht.
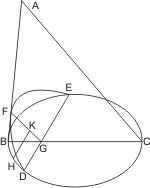 Sei ein Kegel mit dem Scheitel A und dem Grundkreis BC gegeben, und werde derselbe von einer durch die Achse gelegten Ebene in dem Dreieck ABC und von einer zweiten Ebene geschnitten, deren Durchschnittslinie DE mit dem Grundkreis senkrecht auf BC oder seiner Verlängerung steht. Sei nun der durch die zweite Ebene erzeugte Kegelschnitt DFE und FG ihr Durchschnitt mit der Ebene des Achsendreiecks, und werde endlich von einem beliebigen Punkt H des Kegelschnitts eine Parallele HK mit DE gezogen, so wird behauptet, dass HK die Linie FG schneidet, und darüber hinaus bis zum Kegelschnitt verlängert durch FG halbiert werde.
Sei ein Kegel mit dem Scheitel A und dem Grundkreis BC gegeben, und werde derselbe von einer durch die Achse gelegten Ebene in dem Dreieck ABC und von einer zweiten Ebene geschnitten, deren Durchschnittslinie DE mit dem Grundkreis senkrecht auf BC oder seiner Verlängerung steht. Sei nun der durch die zweite Ebene erzeugte Kegelschnitt DFE und FG ihr Durchschnitt mit der Ebene des Achsendreiecks, und werde endlich von einem beliebigen Punkt H des Kegelschnitts eine Parallele HK mit DE gezogen, so wird behauptet, dass HK die Linie FG schneidet, und darüber hinaus bis zum Kegelschnitt verlängert durch FG halbiert werde.
Die Linie HK erfüllt genau die Voraussetzung des vorigen Lehrsatzes, weshalb die Richtigkeit der Behauptung erhellt. Es ist nun entweder der Kegel ein gerader, oder das Achsendreieck ABC senkrecht auf der Ebene des Grundkreises BC, oder keines von beiden der Fall.
Sei nun erstens der Kegel ein gerader, so steht die Ebene ABC auf der Grundfläche BC senkrecht, und da DG senkrecht auf BC steht, muss es auf der Ebene ABC und also auf FG rechtwinklig sein. Derselbe Schluss wird noch Statt finden, wenn der Kegel nicht gerade, aber die Ebene des Achsendreiecks ABC senkrecht auf der Grundfläche BC ist. Ist nun aber keine von beiden der Fall, so kann DG nicht senkrecht auf FG stehen. Denn wäre DGF ein Rechter, so müsste, da DGB nach Annahme ein Rechter ist, DG ein Loth auf der Ebene ABC und also auch die Ebene BDC lothrecht auf ABC sein, was gegen die Annahme ist.
Zusatz. Hieraus erhellt, dass die Linie FG ein Durchmesser des Kegelschnitts DFE ist, da sie alle in demselben einer gegebenen Richtung parallel gezogenen Linien halbiert; und es erhellt zugleich, dass ein Durchmesser die parallelen Linien, die er halbiert, unter schiefem Winkel durchschneiden könne.
Lehrsatz 8. Wenn ein Kegel von einer durch die Achse gelegten Ebene und von einer zweiten Ebene so geschnitten wird, dass die Durchschnittslinien dieser Ebenen mit der Grundfläche senkrecht auf einander stehen, der Durchmesser aber des durch die zweite Ebene entstandenen Kegelschnitts mit einer der an den Scheitel anstossenden Seiten des in der ersten Ebene liegenden Achsendreiecks entweder parallel ist oder jenseit des Scheitels des Kegels zusammentrifft, und wenn sowohl die Kegelfläche als die schneidenden Ebenen ins Unendliche erweitert werden, so setzt sich auch der Kegelschnitt ohne Ende fort und eine von einem beliebigen Punkt desselben mit der in der Grundfläche befindlichen Durchschnittslinie gezogene Parallele schneidet auf dem Durchmesser vom Scheitel an gerechnet immer eine gewisse Länge ab.
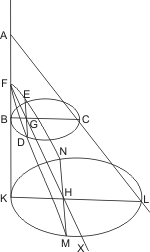 Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben, und werde derselbe von einer durch die Achse gelegten Ebene so geschnitten, dass das Achsendreieck ABC entsteht und von einer zweiten Ebene, deren Durchschnitt DE mit der Grundfläche senkrecht auf BC steht, und welche mit der Kegelfläche die Durchschnittslinie DFE hat; der Durchmesser dieses Kegelschnitts sei FG, welcher mit AC entweder parallel ist, oder jenseit des Scheitels A zusammentrifft, so wird behauptet, dass sich der Kegelschnitt DFE ins Unendliche fortsetze, wenn die Kegelfläche und die schneidende Ebene ins Unendliche erweitert werden. Man verlängere zugleich die Linien AB, AC, FG, so werden nach Voraussetzung AC, FG über C und G verlängert niemals zusammentreffen. Sei nun H ein beliebiger Punkt der verlängerten FG und werde durch H die Linie KHL parallel mit BC und MHN parallel mit DE gezogen, so wird die durch KL, MN gelegte Ebene parallel der durch BC, DE gehenden Grundfläche des Kegels, und folglich ihr Durchschnitt mit der Kegelfläche ein Kreis sein. Da nun die Punkte D, E, M, N sowohl in der zweiten schneidenden Ebene als in der Kegelfläche liegen, so ist gezeigt, dass der Kegelschnitt bis zu den Punkten M, N sich fortsetzt, und also auch ins Unendliche sich fortsetzen wird, wenn sowohl die Kegelfläche als die schneidende Ebene gehörig erweitert werden.
Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben, und werde derselbe von einer durch die Achse gelegten Ebene so geschnitten, dass das Achsendreieck ABC entsteht und von einer zweiten Ebene, deren Durchschnitt DE mit der Grundfläche senkrecht auf BC steht, und welche mit der Kegelfläche die Durchschnittslinie DFE hat; der Durchmesser dieses Kegelschnitts sei FG, welcher mit AC entweder parallel ist, oder jenseit des Scheitels A zusammentrifft, so wird behauptet, dass sich der Kegelschnitt DFE ins Unendliche fortsetze, wenn die Kegelfläche und die schneidende Ebene ins Unendliche erweitert werden. Man verlängere zugleich die Linien AB, AC, FG, so werden nach Voraussetzung AC, FG über C und G verlängert niemals zusammentreffen. Sei nun H ein beliebiger Punkt der verlängerten FG und werde durch H die Linie KHL parallel mit BC und MHN parallel mit DE gezogen, so wird die durch KL, MN gelegte Ebene parallel der durch BC, DE gehenden Grundfläche des Kegels, und folglich ihr Durchschnitt mit der Kegelfläche ein Kreis sein. Da nun die Punkte D, E, M, N sowohl in der zweiten schneidenden Ebene als in der Kegelfläche liegen, so ist gezeigt, dass der Kegelschnitt bis zu den Punkten M, N sich fortsetzt, und also auch ins Unendliche sich fortsetzen wird, wenn sowohl die Kegelfläche als die schneidende Ebene gehörig erweitert werden.
Es erhellt zugleich, dass es möglich ist, in dem Kegelschnitt durch eine Parallele mit DE jede beliebige Länge, vom Durchmesser FH von F gerechnet, abzuschneiden. Denn sei FX irgendeine gegebene LäRnge, so wird die durch X mit DE gezogene Parallele, wie eben von der durch H gelegten gezeigt ist, den Kegelschnitt in zwei Punkten schneiden müssen.
Lehrsatz 9. Wenn ein Kegel von einer Ebene, die beide Schenkelseiten eines Achsendreiecks trifft, und weder der Grundlinie parallel noch ein Wechselschnitt ist, durchschnitten wird, so ist der entstandene Kegelschnitt kein Kreis.
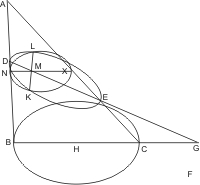 Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben, und werde derselbe von einer Ebene, die weder der Grundfläche parallel noch ein Wechselschnitt ist, geschnitten, so dass der Kegelschnitt DKE entsteht, so wird behauptet, dass DKE kein Kreis sei. Angenommen er wäre ein Kreis, so erweitere man die schneidende Ebene, bis sie die Grundfläche in der Linie FG schneidet, und fälle vom Mittelpunkt H der Grundfläche BC ein Loth HG auf diese Durchschnittslinie; dann lege man durch HG und die Achse des Kegels eine Ebene, welche die Kegelfläche in den Geraden AB und AC trifft, so werden die Punkte D, E, in denen diese Geraden die schneidende Ebene DKE treffen, mit G in gerader Linie liegen, da sie in der Durchschnittslinie der Ebenen ABC, DKE liegen müssen. Sei nun K ein beliebiger Punkt des Kreises DKE, und werde durch K eine Parallele KL mit FG gezogen, so wird dieselbe nach § 7 in ihrem Durchschnittspunkt M mit DE halbiert, und da dieses von allen mit FG parallel gezogenen Sehnen des Kreises DKE gilt, muss DE ein Durchmesser dieses Kreises sein. Da also DE auf KM und folglich auch auf FG lotbrecht steht, ist FG und deshalb auch die Ebene DKE lotbrecht auf der Ebene ABC. Man ziehe nun noch durch M die Parallele NMX mit BC, so wird, da auch KL parallel FG ist, die durch KL, MX gelegte Ebene der Grundfläche parallel und also ein Kreis sein. Nun wäre:
Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben, und werde derselbe von einer Ebene, die weder der Grundfläche parallel noch ein Wechselschnitt ist, geschnitten, so dass der Kegelschnitt DKE entsteht, so wird behauptet, dass DKE kein Kreis sei. Angenommen er wäre ein Kreis, so erweitere man die schneidende Ebene, bis sie die Grundfläche in der Linie FG schneidet, und fälle vom Mittelpunkt H der Grundfläche BC ein Loth HG auf diese Durchschnittslinie; dann lege man durch HG und die Achse des Kegels eine Ebene, welche die Kegelfläche in den Geraden AB und AC trifft, so werden die Punkte D, E, in denen diese Geraden die schneidende Ebene DKE treffen, mit G in gerader Linie liegen, da sie in der Durchschnittslinie der Ebenen ABC, DKE liegen müssen. Sei nun K ein beliebiger Punkt des Kreises DKE, und werde durch K eine Parallele KL mit FG gezogen, so wird dieselbe nach § 7 in ihrem Durchschnittspunkt M mit DE halbiert, und da dieses von allen mit FG parallel gezogenen Sehnen des Kreises DKE gilt, muss DE ein Durchmesser dieses Kreises sein. Da also DE auf KM und folglich auch auf FG lotbrecht steht, ist FG und deshalb auch die Ebene DKE lotbrecht auf der Ebene ABC. Man ziehe nun noch durch M die Parallele NMX mit BC, so wird, da auch KL parallel FG ist, die durch KL, MX gelegte Ebene der Grundfläche parallel und also ein Kreis sein. Nun wäre:
KM2 = NM · MX = DM · ME, also ΔNMD ähnlich ΔMXE und Winkel ANX gleich Winkel AED, also der Schnitt DKE ein Wechselschnitt, was gegen die Annahme ist. Also ist gezeigt, dass DKE nicht ein Kreis sein kann.
Lehrsatz 10. Wenn in einem Kegelschnitt zwei Punkte angenommen werden, so wird ihre Verbindungslinie innerhalb des Kegelschnitts und deren Verlängerung ausserhalb desselben fallen.
Nach § 2 fällt eine solche Verbindungslinie innerhalb des Kegels, also auch innerhalb des Kegelschnitts.
Lehrsatz 11. Wenn ein Kegel von einer durch die Achse gelegten Ebene und von einer zweiten Ebene so geschnitten wird, dass die Durchschnittslinien der beiden Ebenen mit der Grundfläche senkrecht auf einander stehen und wenn der Durchmesser des durch die zweite Ebene erhaltenen Kegelschnitts einer Schenkelseite des Achsendreiecks parallel ist, so ist das Quadrat einer von einem beliebigen Punkt des Kegelschnitts in der zweiten Ebene parallel der in der Grundfläche befindlichen Durchschnittslinie bis zum Durchmesser hin gezogenen Linie gleich dem Rechteck aus dem durch diese Linie vom Durchmesser nach dem Scheitel hin abgeschnittenen Stück und einer andern Länge, welche sich zu dem den Scheitel des Kegels mit dem des Kegelschnitts verbindenden Stück ebenso verhält wie das Quadrat der Grundlinie des Achsendreiecks zu dem Rechteck aus den beiden übrigen Seiten. Ein Kegelschnitt dieser Art heisst eine Parabel.
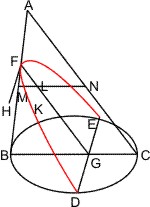 Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben und werde derselbe von einer durch die Achse gelegten Ebene, die das Achsendreieck ABC bildet, und von einer zweiten Ebene geschnitten, deren Durchschnitt DE mit der Grundfläche senkrecht auf der Grundlinie BC des Achsendreiecks steht, und welche in der Kegelfläche die Linie DFE bildet, deren Durchmesser FG parallel. der Seite AC des Achsendreiecks ist; werde ferner in der zweiten Ebene von F aus unter rechtem Winkel gegen FG eine Linie FH gezogen, so dass FH : FA = BC2 : BA · CA ist, und endlich von einem beliebigen Punkte K des Kegelschnitts bis zum Durchmesser hin eine Parallele KL mit der Linie DE; so wird behauptet:
Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben und werde derselbe von einer durch die Achse gelegten Ebene, die das Achsendreieck ABC bildet, und von einer zweiten Ebene geschnitten, deren Durchschnitt DE mit der Grundfläche senkrecht auf der Grundlinie BC des Achsendreiecks steht, und welche in der Kegelfläche die Linie DFE bildet, deren Durchmesser FG parallel. der Seite AC des Achsendreiecks ist; werde ferner in der zweiten Ebene von F aus unter rechtem Winkel gegen FG eine Linie FH gezogen, so dass FH : FA = BC2 : BA · CA ist, und endlich von einem beliebigen Punkte K des Kegelschnitts bis zum Durchmesser hin eine Parallele KL mit der Linie DE; so wird behauptet:
KL2 = FL · FH.
Man ziehe noch durch L die Parallele MN zu der Linie BC, so wird die durch KL, MN gelegte Ebene der Grundfläche parallel und ihr Durchschnitt mit der Kegelfläche ein Kreis sein; da nun nach Annahme DE senkrecht auf BC, ist auch KL senkrecht auf LM und also KL2 = ML · LN. Es ist aber
- ML : FL = BC : AC,
- LN : FA = BC : AB, woraus
- ML · LN : : FL ·> FA = BC2 : AC · AB
- ML · LN : FL · FA = FH : FA, und also:
- KL2 = ML · LN = FL · FH. q.e.d.
Lehrsatz 12. Wenn ein Kegel von einer durch die Achse gelegten Ebene und von einer zweiten Ebene geschnitten wird, so dass die Durchschnittslinien beider Ebenen mit der Grundfläche senkrecht auf einander stehen, und wenn der Durchmesser des durch die zweite Ebene entstandenen Kegelschnitts mit der einen Schenkelseite des in der ersten befindlichen Achsendreiecks jenseit des Scheitels des Kegels zusammentrifft, so wird das Quadrat einer von einem Punkt des Kegelschnitts bis zum Durchmesser hin parallel mit der in der Grundfläche befindlichen Durchschnittslinie gezogenen Ordinate gleich sein einem Rechteck, zu dessen einer Seite (der Länge) das Stück des verlängerten Durchmessers, das von dem Aussenwinkel des Achsendreiecks am Scheitel des Kegels abgeschnitten wird, dasselbe Verhältniss hat, als das Quadrat einer vom Scheitel des Kegels parallel dem Durchmesser des Kegelschnitts bis zur Grundfläche gezogenen Linie zu dem Rechteck der hierdurch in der Grundlinie des Achsendreiecks gebildeten Abschnitte, und dessen andere Seite (die Breite) die von der Ordinate auf dem Durchmesser abgeschnittene Abscisse ist, wenn dieses Rechteck noch vermehrt wird um ein anderes von gleicher Breite, das ähnlich und ähnlich gelegen ist mit einem andern, dessen Seiten das auf dem Durchmesser vom Aussenwinkel an der Spitze des Achsendreiecks abgeschnittene Stück und die Länge des vorerwähnten Rechtecks sind. Ein Kegelschnitt dieser Art heisst eine Hyperbel.
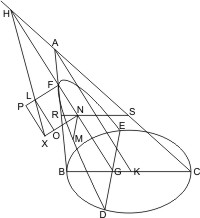 Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben, und werde er von einer Ebene durch die Achse geschnitten, welche das Achsendreieck ABC bildet, und von einer zweiten, welche die Grundfläche in der Linie DE senkrecht auf BC und die Kegelfläche in der Linie DFE durchschneidet, deren Durchmesser GF verlängert mit der Seite AC des Achsendreiecks jenseit des Scheitels in H zusammentrifft. Werde ferner vom Scheitel A mit FG die Parallele AK bis zu ihrem Durchschnitt mit BC und in F in der schneidenden Ebene DFE ein Loth FL auf FG gezogen, so dass AK2 : BK · CK = FH : FL ist; sodann von einem beliebigen Punkte M des entstandenen Kegelschnitts bis zum Durchmesser hin die Linie MN parallel mit DE, endlich von N parallel mit FL die Linie NOX, welche von der Verbindungslinie HL in X getroffen wird, und durch L und X die Linien LO, XP parallel mit FN, so wird behauptet:
Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben, und werde er von einer Ebene durch die Achse geschnitten, welche das Achsendreieck ABC bildet, und von einer zweiten, welche die Grundfläche in der Linie DE senkrecht auf BC und die Kegelfläche in der Linie DFE durchschneidet, deren Durchmesser GF verlängert mit der Seite AC des Achsendreiecks jenseit des Scheitels in H zusammentrifft. Werde ferner vom Scheitel A mit FG die Parallele AK bis zu ihrem Durchschnitt mit BC und in F in der schneidenden Ebene DFE ein Loth FL auf FG gezogen, so dass AK2 : BK · CK = FH : FL ist; sodann von einem beliebigen Punkte M des entstandenen Kegelschnitts bis zum Durchmesser hin die Linie MN parallel mit DE, endlich von N parallel mit FL die Linie NOX, welche von der Verbindungslinie HL in X getroffen wird, und durch L und X die Linien LO, XP parallel mit FN, so wird behauptet:
MN2 = FN · XN.
Man ziehe noch durch N die Linie RS parallel mit BC, so wird die durch MN, RS gelegte Ebene parallel der Grundfläche, also ihr Durchschnitt mit der Kegelfläche ein Kreis, und da nach Annahme DE senkrecht auf BC, also auch MN senkrecht auf RS ist,- MN2 = RN · NS sein. Nun ist
- RN : FN = BK : AK,
- NS : HN = CK : AK, also
- RN · NS : FN · HN = BK · CK : AK2,
- RN ·NS : FN ·HN = XN : HN, und
- MN2 = RN ·NS = FN ·XN. q.e.d.
Lehrsatz 13. Wenn ein Kegel von einer durch die Achse gelegten Ebene und von einer zweiten Ebene geschnitten wird, die beide Schenkelseiten des durch die erste entstandenen Achsendreiecks trifft und weder parallel der Grundfläche noch ein Wechselschnitt ist, und wenn die Durchschnittslinien der beiden Ebenen mit der nöthigenfalls erweiterten Grundfläche senkrecht auf einander stehen, so ist das Quadrat einer von einem beliebigen Punkt des Kegelschnitts parallel der in der Grundfläche befindlichen Durchschnittslinie bis zum Durchmesser gezogenen Ordinate gleich einem Rechteck, zu dessen einer Seite (der Länge) der Durchmesser des Kegelschnitts dasselbe Verhältniss hat, als das Quadrat einer vom Scheitel des Kegels parallel mit dem Durchmesser bis zu der erweiterten Grundfläche gezogenen Linie zu dem Rechteck aus den beiden Abschnitten, welche durch diese auf der verlängerten Grundlinie des Achsendreiecks entstehen, und dessen andere Seite (die Breite) eine der beiden zu der Ordinate gehörigen Abscissen ist, wenn dieses Rechteck noch vermindert wird um ein anderes von gleicher Breite, das ähnlich und ähnlich gelegen ist mit dem zwischen dem Durchmesser und der vorerwähnten Länge des ersten Rechtecks enthaltenen. Ein Kegelschnitt dieser Art heisst eine Ellipse.
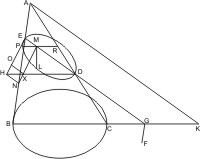 Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben und werde derselbe von einer durch die Achse gelegten Ebene, welche das Achsendreieck ABC bildet, und von einer zweiten Ebene geschnitten, die mit den beiden Seiten AB, AC oder ihren über B und C hinaus gehenden Verlängerungen in den Punkten E und D zusammentrifft, und weder der Grundfläche parallel noch ein Wechselschnitt ist, und deren Durchschnittslinie GF mit der nöthigenfalls erweiterten Grundfläche senkrecht auf der nöthigenfalls verlängerten BC steht. Sei ELD der hierdurch entstandene Kegelschnitt und ED sein Durchmesser, und werde in E in der Ebene ELD ein Loth EH errichtet, so dass, wenn AK eine von dem Scheitel des Kegels parallel mit ED bis zur Grundfläche gezogene Linie ist, ED : EH = AK2 : BK · CK ist, ferner von einem beliebigen Punkt L des Kegelschnitts die Ordinate LM parallel mit der Durchschnittslinie FG gezogen und endlich in M eine Parallele mit EH, die der von D nach H gezogenen Verbindungslinie in X begegnet, und in X und H die Parallelen XO und HN mit DE, so wird behauptet:
Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben und werde derselbe von einer durch die Achse gelegten Ebene, welche das Achsendreieck ABC bildet, und von einer zweiten Ebene geschnitten, die mit den beiden Seiten AB, AC oder ihren über B und C hinaus gehenden Verlängerungen in den Punkten E und D zusammentrifft, und weder der Grundfläche parallel noch ein Wechselschnitt ist, und deren Durchschnittslinie GF mit der nöthigenfalls erweiterten Grundfläche senkrecht auf der nöthigenfalls verlängerten BC steht. Sei ELD der hierdurch entstandene Kegelschnitt und ED sein Durchmesser, und werde in E in der Ebene ELD ein Loth EH errichtet, so dass, wenn AK eine von dem Scheitel des Kegels parallel mit ED bis zur Grundfläche gezogene Linie ist, ED : EH = AK2 : BK · CK ist, ferner von einem beliebigen Punkt L des Kegelschnitts die Ordinate LM parallel mit der Durchschnittslinie FG gezogen und endlich in M eine Parallele mit EH, die der von D nach H gezogenen Verbindungslinie in X begegnet, und in X und H die Parallelen XO und HN mit DE, so wird behauptet:
ML2 = EOXM.
Man ziehe noch durch M die Linie PR parallel mit BC, so ist ähnlich wie in den früheren Sätzen:
- LM2 = PM · MR,
- PM : EM = BK : AK,
- MR : DM = CK : AK, also
- PM · MR : EM · DM = BK · CK : AK2,
- PM · MR : EM · DM = XM : DM, und also
- LM2 = PM · MR = EM · XM. q.e.d.
Die beiden letzten Lehrsätze über Hyperbel und Ellipse lassen folgenden Ausdruck zu: "Werden von beliebigen Punkten eines Kegelschnitts Ordinaten bis zu dem zugehörigen Durchmesser gezogen, so verhält sich bei Ellipse und Hyperbel das Quadrat jeder Ordinate zu dem Rechteck aus den Abschnitten, die sie auf dem Querdurchmesser bildet, wie das zugehörige latus rectum zum latus transversum. Bei der Parabel entsteht durch jede Ordinate auf dem Durchmesser nur ein Abschnitt und verhalten sich die Quadrate der Ordinaten wie die zugehörigen Abschnitte."
Lehrsatz 14. Wenn die am Scheitel zusammenstossenden Kegelflächen von einer nicht durch den Scheitel gehenden Ebene geschnitten werden, so entsteht in jeder der Flächen ein Schnitt, der Hyperbel heisst, und beide Schnitte haben denselben Durchmesser, die Parameter, die zu den Ordinaten gehören, welche der Grundfläche des Kegels parallel sind, sind in beiden gleich, das latus transversum, nämlich die Verbindungslinie der beiden Scheitel, ist beiden gemeinschaftlich. Solche Schnitte heissen Gegenschnittt.
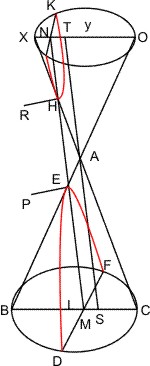 Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben und werde derselbe von einer nicht durch den Scheitel gehenden Ebene, die beide am Scheitel zusammenstossende Kegelflächen trifft, geschnitten, so dass in der einen derselben der Schnitt DEF, in der andern KHG entsteht, so wird behauptet, dass beide Schnitte Hyperbeln sind, die einen gemeinschaftlichen Durchmesser und ein gemeinschaftliches latus transversum so wie gleiche Parameter haben.
Sei ein Kegel mit dem Scheitel A und der Grundfläche BC gegeben und werde derselbe von einer nicht durch den Scheitel gehenden Ebene, die beide am Scheitel zusammenstossende Kegelflächen trifft, geschnitten, so dass in der einen derselben der Schnitt DEF, in der andern KHG entsteht, so wird behauptet, dass beide Schnitte Hyperbeln sind, die einen gemeinschaftlichen Durchmesser und ein gemeinschaftliches latus transversum so wie gleiche Parameter haben.
Man lege eine der Grundfläche parallele Ebene jenseit des Scheitels, die die zweite Kegelfläche in dem Kreis XKOG trifft, ferner falle man vom Mittelpunkt L der Grundfläche ein Loth LM auf die Durchschnittslinie DF dieser Grundfläche mit der Schnittebene, und lege durch ML und eine Ebene, die also auch den Mittelpunkt Y des Kreises XKOG trifft, und in der untern Kegelfläche das Achsendreieck ABC, in der oberen AOX bildet, so wird auch der Durchmesser OX senkrecht auf der Durchschnittslinie KG der Schnittebene mit der Ebene des Kreises XKOG stehen, ferner wird die zuletzt gelegte Ebene die Schnittebene längs der Geraden MEHN und die Kegelflächen in den Geraden BEAO, CAHX treffen. Zieht man nun noch durch A die Parallele SAT mit MN und errichtet in den Punkten E und H der Schnittebene Lothe auf MN, EP und HR, so dass- EH : EP = AS2 : BS · SC und
- EH : HR = AT2 : XT · OT ist
- AS : SB = AT : TO,
- AS : SC = AT : TX,
- AS2 : SB · SC = AT2 : TO · TX,
Lehrsatz 15. Wenn in einer Ellipse von dem Mittelpunkt eines Durchmessers eine zugehörige Ordinate gezogen und nach beiden Seiten bis zum Durchschnitt mit derselben verlängert wird, und wenn sich die so erhaltene ganze Linie zum Durchmesser verhält wie der Durchmesser zu einer dritten Linie, so ist das Quadrat der geraden Linie, die von einem beliebigen Punkt der Ellipse parallel dem Durchmesser bis zur Ordinate gezogen wird, gleich einem Rechteck aus der vorerwähnten dritten Proportionale und dem Stück der Ordinate von der Ellipse bis zu der zuletzt gezogenen Parallelen vermindert um ein anderes Rechteck von derselben Breite, das ähnlich und ähnlich gelegen ist dem aus der verdoppelten Ordinate und der erwähnten dritten Proportionale. Verlängert man diese Parallele über die Ordinate hinaus bis zu ihrem zweiten Durchschnitt mit der Ellipse, so wird sie durch die Ordinate halbiert.
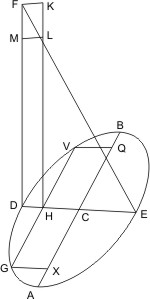 Sei eine Ellipse mit dem Durchmesser AB gegeben und durch die Mitte C des Durchmessers eine zugehörige Ordinate DCE nach beiden Seiten hin bis an den Umfang gezogen. In D errichte man ein Loth DF auf CD, so dass DE : AB = AB : DF ist, und ziehe EF; dann ziehe man von einem beliebigen Punkt G der Ellipse eine Parallele mit AB, bis sie DE in H und verlängert die Ellipse zum zweiten Male in V schneidet, vollende nun das Rechteck HDF zur Ecke K und ziehe durch den Schneidungspunkt L von EF und HK eine Parallele LM mit HD, so wird behauptet:
Sei eine Ellipse mit dem Durchmesser AB gegeben und durch die Mitte C des Durchmessers eine zugehörige Ordinate DCE nach beiden Seiten hin bis an den Umfang gezogen. In D errichte man ein Loth DF auf CD, so dass DE : AB = AB : DF ist, und ziehe EF; dann ziehe man von einem beliebigen Punkt G der Ellipse eine Parallele mit AB, bis sie DE in H und verlängert die Ellipse zum zweiten Male in V schneidet, vollende nun das Rechteck HDF zur Ecke K und ziehe durch den Schneidungspunkt L von EF und HK eine Parallele LM mit HD, so wird behauptet:
- GH2 = DHLM,
- GH = HV.
- GX2 : DC2 = AX · XB : AC2, oder da
AX · XB = AC2 - CX2, - GX2 : DC2 = (AC2 - CX2) : AC2, woraus dividendo.
- DC2 - GX2 : DC2 - CX2 : AV2, da aber
GX = CH, ist DC2 - GX2 = DH · EH, also - DH · EH : DC2 = CX2 : AC2 oder
DH · EH : DE2 = CX2 : AB2, und da nun EH : DE = HL : DF, und
AB2 = DE ·DF ist, ergibt sich - DH · HL : DE ·DF = CX2 : AB2, oder
DH · HL = CX2 = GH2. q.e.d.
AX · XB = AQ ·QB oder
AC2 - CX2 = BC2 - CQ2, da aber AC = BC, ist also auch CX = CQ d.h. GH = HV. [zurück]
Lehrsatz 16. Wenn durch den Punkt, welcher den Querdurchmesser zweier Gegenschnitte halbiert, eine Linie parallel den zugehörigen Ordinaten gezogen wird, so ist dieselbe ein Durchmesser, der dem ersten zugeordnet (conjugirt) genannt wird.
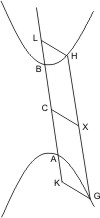 Seien zwei Gegenschnitte GA, HB mit dem Durchmesser AB gegeben und in der Mitte C des letzteren die den zugehörigen Ordinaten parallele CX gezogen, so wird behauptet, dass CD ein dem AB zugeordneter Durchmesser ist.
Seien zwei Gegenschnitte GA, HB mit dem Durchmesser AB gegeben und in der Mitte C des letzteren die den zugehörigen Ordinaten parallele CX gezogen, so wird behauptet, dass CD ein dem AB zugeordneter Durchmesser ist.
Man nehme in einem der Schnitte einen beliebigen Punkt G und ziehe von da eine Parallele mit AB, bis sie den andern Schnitt in B trifft, ziehe in G und H die zugehörigen Ordinaten GK, HL. Da nun nach Anm. zu § 14 GK2 : HL2 KA · KB : LA · LB, GK aber gleich HL, ist auch- KA · KB = LA · LB, oder
- KC2 - AC2 = CL2 - BL2 und da AC= BC, auch KC = LC oder GX = HX. q.e.d.
Zweite Reihe von Erklärungen.
- Der Punkt, welcher einen Durchmesser einer Ellipse oder Hyperbel halbiert, heisst der Mittelpunkt des Kegelschnitts.
- Eine Linie, die vom Mittelpunkt nach dem Umfang gezogen wird, heisst ein Radius oder Halbmesser desselben.
- Auf ähnliche Weise heisst auch der Punkt, welcher das latus transversum zweier Gegenschnitte halbiert, der Mittelpunkt derselben.
- Eine Linie, die vom Mittelpunkt parallel den einem gegebenen Durchmesser zugehörigen Ordinaten gezogen wird, gleich der mittleren Proportionale zwischen dem latus rectum und transversum ist und im Mittelpunkt halbiert wird, heisst der zweite oder conjugirte Durchmesser.
- Das Rechteck aus dem latus transversum und dem latus rectum, die zu einem Durchmesser gehören, heisst das zum Durchmesser gehörige Rechteck.
- Die Linie, welche die Berührungspunkte zweier Tangenten verbindet, heisst die Berührungssehne.
Lehrsatz 17. Wenn vom Endpunkt eines Durchmessers in einem Kegelschnitt eine Linie parallel den zugehörigen Ordinaten gezogen wird, so fällt dieselbe ganz ausserhalb des Kegelschnitts.
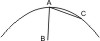 Sei ein Kegelschnitt mit dem Durchmesser AB gegeben, so wird behauptet, dass die vom Scheitel A den zugehörigen Ordinaten parallel gezogene Linie ausserhalb des Kegelschnitts fällt. Denn wäre dies nicht der Fall und schnitte sie den Kegelschnitt in C, so würde, da von einem beliebigen Punkt C des Kegelschnitts die Ordinate CA gezogen ist, diese von dem Durchmesser halbiert werden müssen, also A zugleich Mitte und Endpunkt von CA sein, was unmöglich ist.
Sei ein Kegelschnitt mit dem Durchmesser AB gegeben, so wird behauptet, dass die vom Scheitel A den zugehörigen Ordinaten parallel gezogene Linie ausserhalb des Kegelschnitts fällt. Denn wäre dies nicht der Fall und schnitte sie den Kegelschnitt in C, so würde, da von einem beliebigen Punkt C des Kegelschnitts die Ordinate CA gezogen ist, diese von dem Durchmesser halbiert werden müssen, also A zugleich Mitte und Endpunkt von CA sein, was unmöglich ist.
Lehrsatz 18. Wenn eine Linie einem Kegelschnitt (Parabel oder Hyperbel) begegnet und verlängert nach beiden Seiten zu ausserhalb desselben liegt, und wenn von einem innerhalb desselben befindlichen Punkt eine Parallele mit dieser Linie gezogen wird, so schneidet diese, gehörig verlängert, an beiden Seiten den Kegelschnitt.
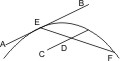 Sei ein Kegelschnitt und die ihn treffende Linie AEB, welche verlängert an beiden Seiten ausserhalb des Kegelschnitts fällt, gegeben, und werde von einem innerhalb desselben befindlichen Punkt C eine Parallele mit AB gezogen, so behaupte ich, dass CD gehörig verlängert an beiden Seiten dem Kegelschnitt begegne. Man nehme irgendeinen Punkt F auf dem Kegelschnitt und verbinde E mit F. Weil nun AB der Linie CD parallel ist, und EF die Linie AB trifft, muss sie auch CD treffen. Wenn nun der Durchschnittspunkt zwischen E und F fällt, ist klar, dass CD nachher den Kegelschnitt treffen muss, da EF ein begränztes Segment desselben abschneidet, wenn aber ausserhalb E, muss CD den Kegelschnitt schon vorher getroffen haben. Also trifft CD nach der Richtung EB zu verlängert den Kegelschnitt. Auf gleiche Weise kann gezeigt werden, dass sie auch nach der Seite EA hin demselben. begegne, wozu nur nöthig ist eine Sehne EF, auf der andern Seite des Punktes C zu ziehen und dann ebenso wie oben zu schliessen. Folglich schneidet CD gehörig verlängert an beiden Seiten den Kegelschnitt.
Sei ein Kegelschnitt und die ihn treffende Linie AEB, welche verlängert an beiden Seiten ausserhalb des Kegelschnitts fällt, gegeben, und werde von einem innerhalb desselben befindlichen Punkt C eine Parallele mit AB gezogen, so behaupte ich, dass CD gehörig verlängert an beiden Seiten dem Kegelschnitt begegne. Man nehme irgendeinen Punkt F auf dem Kegelschnitt und verbinde E mit F. Weil nun AB der Linie CD parallel ist, und EF die Linie AB trifft, muss sie auch CD treffen. Wenn nun der Durchschnittspunkt zwischen E und F fällt, ist klar, dass CD nachher den Kegelschnitt treffen muss, da EF ein begränztes Segment desselben abschneidet, wenn aber ausserhalb E, muss CD den Kegelschnitt schon vorher getroffen haben. Also trifft CD nach der Richtung EB zu verlängert den Kegelschnitt. Auf gleiche Weise kann gezeigt werden, dass sie auch nach der Seite EA hin demselben. begegne, wozu nur nöthig ist eine Sehne EF, auf der andern Seite des Punktes C zu ziehen und dann ebenso wie oben zu schliessen. Folglich schneidet CD gehörig verlängert an beiden Seiten den Kegelschnitt.
Lehrsatz 19. In einem Kegelschnitt trifft jede gerade Linie, die vom Durchmesser aus parallel den zugehörigen Ordinaten gezogen wird, den Kegelschnitt.
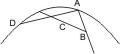 Sei ein Kegelschnitt mit dem Durchmesser AB gegeben und werde ein beliebiger Punkt B darauf angenommen, und von .B eine Linie BC parallel den zu diesem Durchmesser gehörigen Ordinaten gezogen, so wird behauptet, dass BC, gehörig verlängert, den Kegelschnitt trifft. Man nehme einen beliebigen Punkt D im Kegelschnitt, so wird die von A nach D gezogene Linie innerhalb des Kegelschnitts fallen. Weil aber die von A aus den zum Durchmesser AB gehörigen Ordinaten parallel gezogene Linie (nach § 17.) ausserhalb des Kegelschnitts liegt, AD aber denselben trifft, wird eine von B aus den Ordinaten parallel gezogene Linie BC mit AD zusammentreffen müssen. Wenn dies nun zwischen A und D geschieht, wird BC nachher den Kegelschnitt treffen müssen, wenn aber jenseit D, muss sie schon vorher den Kegelschnitt geschnitten haben. Also schneidet die von einem beliebigen Punkt des Durchmessers oder zugehörigen Ordinaten parallel gezogene Linie den Kegelschnitt.
Sei ein Kegelschnitt mit dem Durchmesser AB gegeben und werde ein beliebiger Punkt B darauf angenommen, und von .B eine Linie BC parallel den zu diesem Durchmesser gehörigen Ordinaten gezogen, so wird behauptet, dass BC, gehörig verlängert, den Kegelschnitt trifft. Man nehme einen beliebigen Punkt D im Kegelschnitt, so wird die von A nach D gezogene Linie innerhalb des Kegelschnitts fallen. Weil aber die von A aus den zum Durchmesser AB gehörigen Ordinaten parallel gezogene Linie (nach § 17.) ausserhalb des Kegelschnitts liegt, AD aber denselben trifft, wird eine von B aus den Ordinaten parallel gezogene Linie BC mit AD zusammentreffen müssen. Wenn dies nun zwischen A und D geschieht, wird BC nachher den Kegelschnitt treffen müssen, wenn aber jenseit D, muss sie schon vorher den Kegelschnitt geschnitten haben. Also schneidet die von einem beliebigen Punkt des Durchmessers oder zugehörigen Ordinaten parallel gezogene Linie den Kegelschnitt.
Lehrsatz 20. Die Quadrate zweier Ordinaten, die an denselben Durchmesser einer Parabel gezogen sind, verhalten sich wie die Abschnitte desselben vom Scheitel bis zu den Fusspunkten.
Wendet man Zeile 5. des Beweises von § 11 auf zwei verschiedene Punkte K1, K2 an, so hat man K1L12 : K2L22 = FL1 : FL2. q.e.d.
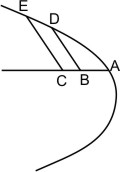 Anm. d. Eutoc. Fig. 18. Hieraus ergiebt sich ein Mittel für die Construction der Parabel durch einzelne Punkte. Man ziehe eine gerade Linie mit dem festen Endpunkt A und von beliebigen Punkten derselben B, C unter beliebigem Winkel die Parallelen BD, CE, so dass BD2 :CE2 = BA : CA, so sind D, E zwei Punkte der Parabel, deren Scheitel A ist.
Anm. d. Eutoc. Fig. 18. Hieraus ergiebt sich ein Mittel für die Construction der Parabel durch einzelne Punkte. Man ziehe eine gerade Linie mit dem festen Endpunkt A und von beliebigen Punkten derselben B, C unter beliebigem Winkel die Parallelen BD, CE, so dass BD2 :CE2 = BA : CA, so sind D, E zwei Punkte der Parabel, deren Scheitel A ist.
Lehrsatz 21. Wenn in einer Hyperbel oder Ellipse oder in einem Kreis Ordinaten gezogen werden, so verhält sich das Quadrat einer jeden derselben zu dem Rechteck der Abschnitte, die sie auf dem Latus transversum bildet, wie das Latus rectum zum Latus transversum; also die Quadrate zweier Ordinaten unter sich wie die Rechtecke aus den auf dem Latus transversum entstandenen Abschnitten.
Setzt man in Zeile 5 des Beweises zu § 12 statt RN · SN seinen Werth MN2 und statt XN : HN das gleiche Verhältniss LF : HF, so erhält man den ersten Theil der Behauptung für die Hyperbel, und wenn man diesen auf zwei beliebige Punkte der Hyperbel anwendet, durch Vergleichung leicht den zweiten Theil. Auf ähnliche Weise verfährt man mit Zeile 5 in § 13, dann hat man den Satz auch für die Ellipse.Anm. 1 des Eutocius. Beim Kreis ist das Latus rectum gleich dem Latus transversum und die Ordinaten stehen senkrecht auf dem Durchmesser.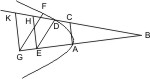 Anm. 2 desselben. Aus dem Lehrsatz ergiebt sich die folgende Construction einer Hyperbel. Sei AB eine gerade Linie, die über A hinaus beliebig verlängert wird, in A die Länge AC senkrecht dagegen gezogen, und B mit C verbunden. In beliebigen Punkten E, G der verlängerten BA errichte man Lothe EH, GK, bis sie die verlängerte BC in H, K schneiden, und ziehe unter beliebigem Winkel von E und G die Parallelen ED, GF, so dass DE2 = AE · EH und FG2 = AG · GK ist, so sind D, F Punkte der Hyperbel. Auf ähnliche Weise verfährt man bei der Ellipse.
Anm. 2 desselben. Aus dem Lehrsatz ergiebt sich die folgende Construction einer Hyperbel. Sei AB eine gerade Linie, die über A hinaus beliebig verlängert wird, in A die Länge AC senkrecht dagegen gezogen, und B mit C verbunden. In beliebigen Punkten E, G der verlängerten BA errichte man Lothe EH, GK, bis sie die verlängerte BC in H, K schneiden, und ziehe unter beliebigem Winkel von E und G die Parallelen ED, GF, so dass DE2 = AE · EH und FG2 = AG · GK ist, so sind D, F Punkte der Hyperbel. Auf ähnliche Weise verfährt man bei der Ellipse.
Lehrsatz 22. Jede Sehne einer Parabel oder Hyperbel, die den Durchmesser nicht innerhalb des Kegelschnitts schneidet, trifft ihn ausserhalb.
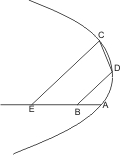 Sei eine Parabel oder Hyperbel mit dem Durchmesser AB, und eine Sehne CD, die den Durchmesser nicht innerhalb trifft, gegeben, so wird behauptet, dass die verlängerte CD ausserhalb des Kegelschnitts mit AB zusammentrifft. Man ziehe von C und D die Ordinaten CE, DB und betrachte zuerst die Parabel. Dann ist CE2 : DB2 = AE : AB, da aber AE > AB, muss auch CE > DB also kann nicht CD parallel AB sein, und da es nicht innerhalb mit AB zusammentrifft, muss es ausserhalb des Kegelschnitts geschehen.
Sei eine Parabel oder Hyperbel mit dem Durchmesser AB, und eine Sehne CD, die den Durchmesser nicht innerhalb trifft, gegeben, so wird behauptet, dass die verlängerte CD ausserhalb des Kegelschnitts mit AB zusammentrifft. Man ziehe von C und D die Ordinaten CE, DB und betrachte zuerst die Parabel. Dann ist CE2 : DB2 = AE : AB, da aber AE > AB, muss auch CE > DB also kann nicht CD parallel AB sein, und da es nicht innerhalb mit AB zusammentrifft, muss es ausserhalb des Kegelschnitts geschehen.
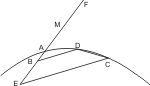 Betrachtet man nun die Hyperbel, deren latus transversum AF sei, so ist CE2 : DB2 = AE · FE : AB · FB, und da AE · FE > AB · FB, auch CE > DB, weshalb CD mit AB zusammentreffen muss, und da es nicht innerhalb geschehen kann, so muss also CD ausserhalb des Kegelschnitts mit AB zusammentreffen.
Betrachtet man nun die Hyperbel, deren latus transversum AF sei, so ist CE2 : DB2 = AE · FE : AB · FB, und da AE · FE > AB · FB, auch CE > DB, weshalb CD mit AB zusammentreffen muss, und da es nicht innerhalb geschehen kann, so muss also CD ausserhalb des Kegelschnitts mit AB zusammentreffen.
Anm. Bei der Hyperbel ist leicht zu zeigen, dass CD zwischen A und der Mitte M des Latus transversum die Linie AB durchschneiden muss. Denn man verwandelt obige Proportion leicht in CE2 : DB2 = ME2 - MA2 : MB2 - MA2 und da ME > MB, muss CE2 : DB2 > ME2 : MB2 (wenn man zu Zähler und Nenner eines unechten Bruchs Gleiches addiert, wird der Bruch kleiner), also auch CE : DB > ME : MB, woraus die Behanptung erhellt.
Lehrsatz 23. Jede Sehne einer Ellipse, welche zwei conjugirte Durchmesser innerhalb der Ellipse nicht schneidet, trifft dieselben ausserhalb.
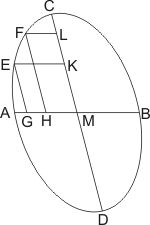 Sei eine Ellipse mit den conjugirten Durchmessern AB, CD gegeben, und zwischen den Endpunkten A und C derselben zwei Punkte E und F in dem Umfang angenommen und durch eine gerade Linie verbunden, so wird behauptet, dass EF, verlängert, beide Durchmesser ausserhalb des Kegelschnitts treffe. Man ziehe von den Punkten E und F gegen den Durchmesser AB hin die Ordinaten EG, FH, und gegen CD hin EK, FL, so ist
Sei eine Ellipse mit den conjugirten Durchmessern AB, CD gegeben, und zwischen den Endpunkten A und C derselben zwei Punkte E und F in dem Umfang angenommen und durch eine gerade Linie verbunden, so wird behauptet, dass EF, verlängert, beide Durchmesser ausserhalb des Kegelschnitts treffe. Man ziehe von den Punkten E und F gegen den Durchmesser AB hin die Ordinaten EG, FH, und gegen CD hin EK, FL, so ist
- EG2 : FH2 = AG · BG : AH · BH,
- FL2 : EK2 = CL · LD : CK · KD.
Lehrsatz 24. Wenn eine gerade Linie einer Parabel oder Hyperbel in einem Punkte begegnet und nach beiden Seiten hin ausserhalb des Kegelschnitts liegt, so wird dieselbe den Durchmesser schneiden.
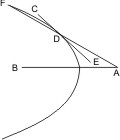 Sei eine Parabel oder Hyperbel mit dem Durchmesser AB gegeben, und begegne ihr die gerade Linie CDE im Punkte D, so dass sie zu beiden Seiten von D ausserhalb des Kegelschnitts fällt, so wird behauptet, dass CDE den Durchmesser AB schneidet. Man nehme auf der von D aus dem Scheitel abgewandten Seite des Kegelschnitts den Punkt F beliebig an und ziehe FD, so wird diese Linie nach § 22 den Durchmesser schneiden. Sei A der Durchschnittspunkt. Da nun CDE mit dem Theile DE zwischen die Gerade DA und den Kegelschnitt fällt, muss sie den Durchmesser zwischen dem Scheitel und dem Punkt A treffen.
Sei eine Parabel oder Hyperbel mit dem Durchmesser AB gegeben, und begegne ihr die gerade Linie CDE im Punkte D, so dass sie zu beiden Seiten von D ausserhalb des Kegelschnitts fällt, so wird behauptet, dass CDE den Durchmesser AB schneidet. Man nehme auf der von D aus dem Scheitel abgewandten Seite des Kegelschnitts den Punkt F beliebig an und ziehe FD, so wird diese Linie nach § 22 den Durchmesser schneiden. Sei A der Durchschnittspunkt. Da nun CDE mit dem Theile DE zwischen die Gerade DA und den Kegelschnitt fällt, muss sie den Durchmesser zwischen dem Scheitel und dem Punkt A treffen.
Lehrsatz 25. Wenn eine gerade Linie einer Ellipse zwischen den Endpunkten zweier conjugirten Durchmesser in einem Punkte begegnet und zu beiden Seiten desselben ausserhalb der Ellipse fällt, so wird sie beide Durchmesser schneiden.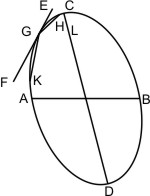 Sei eine Ellipse mit den conjugirten Durchmessern AB und CD gegeben, und werde dieselbe zwischen den Endpunkten A und C der Durchmesser von der Geraden EF im Punkte G so getroffen, dass diese Linie zu beiden Seiten von G ausserhalb des Kegelschnitts liegt, so wird behauptet, dass EF, verlängert, beide Durchmesser ausserhalb des Kegelschnitts schneidet. Man ziehe von G auf der dem Scheitel A abgewandten Seite die Sehne GH, so dass H zwischen G und C liegt, dann schneidet nach § 23 die verlängerte HG den Durchmesser BA; da nun EF mit dem Theile GF zwischen die verlängerte HG und die Ellipse fällt, muss sie den verlängerten Durchmesser BA noch früher schneiden. Ein Gleiches kann in Bezug auf den Durchmesser CD durch eine nach der andern Seite gezogene Sehne bewiesen werden.
Sei eine Ellipse mit den conjugirten Durchmessern AB und CD gegeben, und werde dieselbe zwischen den Endpunkten A und C der Durchmesser von der Geraden EF im Punkte G so getroffen, dass diese Linie zu beiden Seiten von G ausserhalb des Kegelschnitts liegt, so wird behauptet, dass EF, verlängert, beide Durchmesser ausserhalb des Kegelschnitts schneidet. Man ziehe von G auf der dem Scheitel A abgewandten Seite die Sehne GH, so dass H zwischen G und C liegt, dann schneidet nach § 23 die verlängerte HG den Durchmesser BA; da nun EF mit dem Theile GF zwischen die verlängerte HG und die Ellipse fällt, muss sie den verlängerten Durchmesser BA noch früher schneiden. Ein Gleiches kann in Bezug auf den Durchmesser CD durch eine nach der andern Seite gezogene Sehne bewiesen werden.
Lehrsatz 26. Wenn in einer Parabel oder Hyperbel eine gerade Linie parallel mit dem Durchmesser des Schnitts gezogen wird, so trifft dieselbe den Kegelschnitt in einem und nicht in mehreren Punkten.
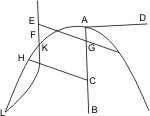 Sei zuerst eine Parabel mit dem Durchmesser AB und dem latus rectum AD gegeben, und EF parallel dem Durchmesser gezogen, so wird behauptet, dass EF die Parabel schneidet. Seie E ein Punkt ausserhalb der Parabel und werde EG parallel den zum Durchmesser gehörigen Ordinaten gezogen, ferner nehme man in AB einen Punkt C so an, dass AD · AC > EG2 ist, und ziehe in C die Ordinate CH, so wird also auch CH2 > EG2, also muss EF, ehe sie HC trifft, den Kegelschnitt getroffen haben. Sei K der Schneidungspunkt, so wird behauptet, dass kein zweiter möglich ist. Denn wäre ein solcher, etwa L, vorhanden, so müsste nach § 22 die gerade Linie LK den Durchmesser AB ausserhalb treffen, was gegen die Annahme ist.
Sei zuerst eine Parabel mit dem Durchmesser AB und dem latus rectum AD gegeben, und EF parallel dem Durchmesser gezogen, so wird behauptet, dass EF die Parabel schneidet. Seie E ein Punkt ausserhalb der Parabel und werde EG parallel den zum Durchmesser gehörigen Ordinaten gezogen, ferner nehme man in AB einen Punkt C so an, dass AD · AC > EG2 ist, und ziehe in C die Ordinate CH, so wird also auch CH2 > EG2, also muss EF, ehe sie HC trifft, den Kegelschnitt getroffen haben. Sei K der Schneidungspunkt, so wird behauptet, dass kein zweiter möglich ist. Denn wäre ein solcher, etwa L, vorhanden, so müsste nach § 22 die gerade Linie LK den Durchmesser AB ausserhalb treffen, was gegen die Annahme ist.
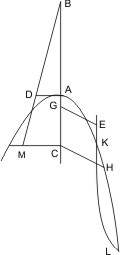 Sei zweitens eine Hyperbel mit dem latus rectum AD und dem latus transversum AB gegeben; man verfahre wie oben, ziehe von C parallel mit AD die Linie CM, bis sie die verlängerte BD in M schneidet, so wird, da DA · AC > EG2 nach Annahme und CM · AC > DA · AC, wie leicht erhellt, und endlich HC2 = AC · CM, auch HC2 > EG2 sein, woraus, wie oben, die Behauptung weiter gefolgert werden kann.
Sei zweitens eine Hyperbel mit dem latus rectum AD und dem latus transversum AB gegeben; man verfahre wie oben, ziehe von C parallel mit AD die Linie CM, bis sie die verlängerte BD in M schneidet, so wird, da DA · AC > EG2 nach Annahme und CM · AC > DA · AC, wie leicht erhellt, und endlich HC2 = AC · CM, auch HC2 > EG2 sein, woraus, wie oben, die Behauptung weiter gefolgert werden kann.
Lehrsatz 27. Wenn eine gerade Linie den Durchmesser einer Parabel schneidet, so trifft sie gehörig verlängert an beiden Seiten den Kegelschnitt.
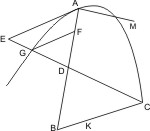 Sei eine Parabel mit dem Durchmesser AB und eine gerade Linie CD, die den Durchmesser innerhalb des Kegelschnitts in D schneidet, gegeben, so wird behauptet, dass CD, gehörig verlängert, an beiden Seiten den Kegelschnitt schneidet. Man ziehe vom Scheitel A die Linie AE parallel den zugehörigen Ordinaten, so wird AE nach § 17 ausserhalb des Kegelschnitts fallen. Es wird nun CD entweder mit AE parallel sein oder nicht. Im ersten Fall ist CD also den Ordinaten parallel und trifft deshalb nach § 19 den Kegelschnitt. Ist sie aber nicht parallel, so verlängere man sie, bis sie AE im Punkte E schneidet, dann wird CD, ehe sie AE schneidet, den Kegelschnitt schon getroffen haben müssen. Es wird nun noch behauptet, dass CD auch nach der andern Seite hin verlängert, den Kegelschnitt schneiden muss. Sei AM das latus rectum und werde von dem schon nachgewiesenen Schneidungspunkt zwischen CD und dem Kegelschnitt die Ordinate GF gezogen, auf AB ein Punkt B bestimmt, so dass AD2 = AF · AB, und in B den Ordinaten parallel die Linie BK gezogen, bis sie die gegebene CD in C trifft, so wird behauptet, dass C der zweite Durchschnittspunkt der gegebenen Geraden CD mit der Parabel ist.
Sei eine Parabel mit dem Durchmesser AB und eine gerade Linie CD, die den Durchmesser innerhalb des Kegelschnitts in D schneidet, gegeben, so wird behauptet, dass CD, gehörig verlängert, an beiden Seiten den Kegelschnitt schneidet. Man ziehe vom Scheitel A die Linie AE parallel den zugehörigen Ordinaten, so wird AE nach § 17 ausserhalb des Kegelschnitts fallen. Es wird nun CD entweder mit AE parallel sein oder nicht. Im ersten Fall ist CD also den Ordinaten parallel und trifft deshalb nach § 19 den Kegelschnitt. Ist sie aber nicht parallel, so verlängere man sie, bis sie AE im Punkte E schneidet, dann wird CD, ehe sie AE schneidet, den Kegelschnitt schon getroffen haben müssen. Es wird nun noch behauptet, dass CD auch nach der andern Seite hin verlängert, den Kegelschnitt schneiden muss. Sei AM das latus rectum und werde von dem schon nachgewiesenen Schneidungspunkt zwischen CD und dem Kegelschnitt die Ordinate GF gezogen, auf AB ein Punkt B bestimmt, so dass AD2 = AF · AB, und in B den Ordinaten parallel die Linie BK gezogen, bis sie die gegebene CD in C trifft, so wird behauptet, dass C der zweite Durchschnittspunkt der gegebenen Geraden CD mit der Parabel ist.
Es ist- GF : BC = DF : BD, und da nach Annahme AF : AD = AD : AB auch dividendo DF : BD = AB : AB, also
- GF2 : BC2 = AD2 : AB2.
- GF2 : BC2 = AF : AB und folglich, da G auf der Parabel liegt, befindet sich auch C auf der selben. q. e. d.
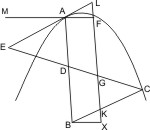 Zweiter Beweis. Sei eine Parabel mit dem Durchmesser AB und der den Durchmesser schneidenden Linie CD gegeben, so wird behauptet, dass CD verlängert den Kegelschnitt an beiden Seiten schneide. Man ziehe in A den Ordinaten parallel AE; ist nun CD parallel AE, so schneidet es nach § 17 den Kegelschnitt; ist es aber nicht parallel, so schneidet es AE in E; dann sei AM: das latus rectum nach derselben Seite als AE gezogen, und auf der verlängerten MA das Stück AF dergestalt abgeschnitten, dass AE2 : ΔAED = AM : AF; ferner ziehe man durch F die Parallele FG mit AB, welche DC in G schneidet, verlängere EA, bis es die Parallele in L trifft, und bestimme eine Parallele CB mit AE dergestalt, dass das durch dieselbe von dem Winkel EGL oder seinem Scheitelwinkel abgeschnittene Dreieck GCK gleich dem Viereck LADG ist, so wird behauptet, dass der Punkt C, in welchem diese Parallele die Gerade DC trifft, sich auf der Parabel befindet. Sei zuerst die Parallele durch den Scheitelwinkel von EGL gelegt, und schneide sie FG in K. Man vollende noch das Rechteck FABX. Nun ist:
Zweiter Beweis. Sei eine Parabel mit dem Durchmesser AB und der den Durchmesser schneidenden Linie CD gegeben, so wird behauptet, dass CD verlängert den Kegelschnitt an beiden Seiten schneide. Man ziehe in A den Ordinaten parallel AE; ist nun CD parallel AE, so schneidet es nach § 17 den Kegelschnitt; ist es aber nicht parallel, so schneidet es AE in E; dann sei AM: das latus rectum nach derselben Seite als AE gezogen, und auf der verlängerten MA das Stück AF dergestalt abgeschnitten, dass AE2 : ΔAED = AM : AF; ferner ziehe man durch F die Parallele FG mit AB, welche DC in G schneidet, verlängere EA, bis es die Parallele in L trifft, und bestimme eine Parallele CB mit AE dergestalt, dass das durch dieselbe von dem Winkel EGL oder seinem Scheitelwinkel abgeschnittene Dreieck GCK gleich dem Viereck LADG ist, so wird behauptet, dass der Punkt C, in welchem diese Parallele die Gerade DC trifft, sich auf der Parabel befindet. Sei zuerst die Parallele durch den Scheitelwinkel von EGL gelegt, und schneide sie FG in K. Man vollende noch das Rechteck FABX. Nun ist:
- EA2 : ΔEAD = CB2 : ΔCBD, und da ΔCGK = LADG und EA2 : ΔEAD = AM : AF, auch ALKB = AFXB, so ist
- CB2 : AFXB AM : AF, also
- CB2 = AM · AB, und folglich liegt der Punktz C auf der Parabel.
Lehrsatz 28. Wenn eine gerade Linie den einen von zwei Gegenschnitten berührt, und durch einen innerhalb des andern angenommenen Punkt damit eine Parallele gezogen wird, so wird diese, gehörig verlängert, an beiden Seiten mit dem Gegenschnitt zusammentreffen.
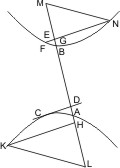 Seien zwei Gegenschnitte mit den Scheiteln A und B, und in dem einen, dessen Scheitel A ist, eine Tangente CD gegeben, und werde in dem andern ein Punkt E angenommen und durch denselben eine Parallele EF mit CD gezogen, so wird behauptet, dass EF an beiden Seiten mit dem Kegelschnitt zusammentreffe.
Seien zwei Gegenschnitte mit den Scheiteln A und B, und in dem einen, dessen Scheitel A ist, eine Tangente CD gegeben, und werde in dem andern ein Punkt E angenommen und durch denselben eine Parallele EF mit CD gezogen, so wird behauptet, dass EF an beiden Seiten mit dem Kegelschnitt zusammentreffe.
Da bewiesen ist, dass CD, gehörig verlängert, den Durchmesser schneidet (s. § 24), und EF parallel CD ist, wird auch EF denselben treffen; sei G der Schneidungspunkt, und werde in dem andern Schnitt AH gleich GB genommen, durch H eine Parallele HK mit CD gezogen, bis sie den Kegelschnitt in K trifft und von K die Ordinate KL gezogen. Man setze nun GM = HL und ziehe von M eine Parallele mit KL, bis sie FE in N schneidet. Da nun ΔKLH congruent ΔNMG ist, wird KL = MN, und da LA · LB = MA · MB ist, liegt der Punkt N auf dem Kegelschnitt. Auf dieselbe Weise wird gezeigt, dass FE an der andern Seite den Kegelschnitt trifft.
Lehrsatz 29. Wenn in zwei Gegenschnitten eine durch den Mittelpunkt gezogene gerade Linie dem einen Schnitt begegnet, so trifft sie auch den andern.
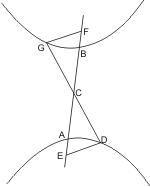 Seien zwei Gegenschnitte mit dem Durchmesser AB und der durch das Centrum gehenden Geraden CD gegeben, welche den einen Schnitt mit dem Scheitel A in D trifft, so wird behauptet, dass CD, gehörig verlängert, auch den andern Schnitt treffe.
Seien zwei Gegenschnitte mit dem Durchmesser AB und der durch das Centrum gehenden Geraden CD gegeben, welche den einen Schnitt mit dem Scheitel A in D trifft, so wird behauptet, dass CD, gehörig verlängert, auch den andern Schnitt treffe.
Man ziehe von D die Ordinate DE, setze CF = CE und ziehe von F die Parallele FG mit DE, welche die verlängerte DC in G schneidet; da nun DE = FG und EA · EB = FA · FB, wird der Punkt G auf dem Kegelschnitt sich befinden.
Lehrsatz 30. Wenn in zwei Gegenschnitten oder in einer Ellipse eine gerade Linie durch den Mittelpunkt gezogen wird, und, verlängert, an beiden Seiten dem Kegelschnitt begegnet, so wird sie im Mittelpunkt halbiert werden.
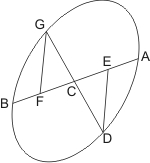 Wenn alles wie im vorigen Satz eingerichtet ist, so folgt aus der Congruenz der Dreiecke CDE und CFG leicht, dass DC = CG. Und auf gleiche Weise wird es auch für die Ellipse bewiesen.
Wenn alles wie im vorigen Satz eingerichtet ist, so folgt aus der Congruenz der Dreiecke CDE und CFG leicht, dass DC = CG. Und auf gleiche Weise wird es auch für die Ellipse bewiesen.
Lehrsatz 31. Wenn im latus transversum einer Hyperbel ein Punkt jenseit des Mittelpunkts angenommen und von da eine gerade Linie gezogen wird, die den Kegelschnitt trifft, so wird ihre Verlängerung über diesen Durchschnittspunkt innerhalb der Hyperbel liegen.
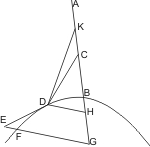 Sei eine Hyperbel mit dem Durchmesser AB gegeben, und werde von dem Mittelpunkt C desselben eine Linie CD gezogen, die den Kegelschnitt in D trifft, so wird behauptet, dass die Verlängerung von CD innerhalb des Kegelschnitts fällt.
Sei eine Hyperbel mit dem Durchmesser AB gegeben, und werde von dem Mittelpunkt C desselben eine Linie CD gezogen, die den Kegelschnitt in D trifft, so wird behauptet, dass die Verlängerung von CD innerhalb des Kegelschnitts fällt.
Sie falle, wenn möglich, ausserhalb und sei E ein Punkt in ihr. Man ziehe von D die Ordinate DH und von E die Parallele EG, die den Kegelschnitt in F trifft, so ist- EG2 : DH2 > GA · GB : HA · HB,
- CG2 : CH2 > CG2 - CB2 : CH2 - CB2
Zusatz. Aus dem schon Bewiesenen folgt, dass eine Tangente der Hyperbel den Durchmesser zwischen dem Scheitel und dem Mittelpunkt schneiden muss.
Lehrsatz 32. Wenn durch den Scheitel eines Kegelschnitts eine Linie parallel den zugehörigen Ordinaten gezogen wird, so berührt sie den Kegelschnitt und in den Raum zwischen dem Kegelschnitt und dieser Geraden kann keine andere gerade Linie fallen.
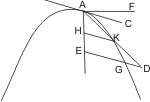 Sei zuerst eine Parabel mit dem Durchmesser AB gegeben, und werde von dem Scheitel A eine den Ordinaten parallele Linie AC gezogen, so fällt AC nach § 17 ausserhalb des Kegelschnitts. Es wird behauptet, dass in dem Raum zwischen AC und dem Kegelschnitt von A aus keine zweite Gerade gezogen werden kann. Denn wäre das möglich, so sei AD eine solche Gerade; und werde von dem beliebigen Punkte D derselben den Ordinaten parallel DE gezogen, welche den Kegelschnitt in G schneidet. Ist nun AF das latus rectum, so wird
Sei zuerst eine Parabel mit dem Durchmesser AB gegeben, und werde von dem Scheitel A eine den Ordinaten parallele Linie AC gezogen, so fällt AC nach § 17 ausserhalb des Kegelschnitts. Es wird behauptet, dass in dem Raum zwischen AC und dem Kegelschnitt von A aus keine zweite Gerade gezogen werden kann. Denn wäre das möglich, so sei AD eine solche Gerade; und werde von dem beliebigen Punkte D derselben den Ordinaten parallel DE gezogen, welche den Kegelschnitt in G schneidet. Ist nun AF das latus rectum, so wird
- DE2 : AE2 > GE2 : AE2, und da GE2 = AE · AF,
- DE2 : AE2 > AF : AE.
- DE2 : AE2 = AF : AH
- HK2 : AH2 = AF : AH oder HK2 = AH · AF.
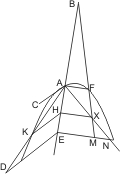 Sei zweitens der Schnitt eine Hyperbel oder Ellipse oder ein Kreis mit dem Durchmesser AB, AF das latus rectum, und werde BF gezogen.
Zieht man nun in A die Linie AC den Ordinaten parallel, so fällt dieselbe ausserhalb des Kegelschnitts nach § 17. Es wird behauptet, dass in den Raum zwischen der Geraden AC und dem Kegelschnitt eine zweite Gerade nicht fallen könne. Denn wäre dies möglich, so sei AD eine solche Gerade, und von einem beliebigen Punkte D derselben werde den Ordinaten parallel die Linie DE an den Durchmesser gezogen, welche den Kegelschnitt in G trifft. In E ziehe man EM parallel mit AF, bis zum Durchschnitt N mit BF. Nun ist
Sei zweitens der Schnitt eine Hyperbel oder Ellipse oder ein Kreis mit dem Durchmesser AB, AF das latus rectum, und werde BF gezogen.
Zieht man nun in A die Linie AC den Ordinaten parallel, so fällt dieselbe ausserhalb des Kegelschnitts nach § 17. Es wird behauptet, dass in den Raum zwischen der Geraden AC und dem Kegelschnitt eine zweite Gerade nicht fallen könne. Denn wäre dies möglich, so sei AD eine solche Gerade, und von einem beliebigen Punkte D derselben werde den Ordinaten parallel die Linie DE an den Durchmesser gezogen, welche den Kegelschnitt in G trifft. In E ziehe man EM parallel mit AF, bis zum Durchschnitt N mit BF. Nun ist
- DE2 : AE > GE2 : AE2, und da GE2 = AE · EM,
- DE2 : AE2 > EM : AE.
- DE2 : AE2 = EN : AE,
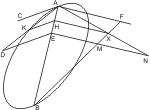 ziehe AN, welche BF in X schneidet, ziehe von X die Linie XH parallel mit AF bis zum Durchmesser und von H den Ordinaten parallel HK bis zum Durchschnitt K mit der Geraden AD; da nun DE2 : AE2 = KH2 : AH2 und EN : AE = HX : AH, so giebt dies in (3) eingesetzt:
ziehe AN, welche BF in X schneidet, ziehe von X die Linie XH parallel mit AF bis zum Durchmesser und von H den Ordinaten parallel HK bis zum Durchschnitt K mit der Geraden AD; da nun DE2 : AE2 = KH2 : AH2 und EN : AE = HX : AH, so giebt dies in (3) eingesetzt:
- KH2 : AH2 = HX : AH oder KH2 = AH · HX;
Lehrsatz 33. Wenn von einem Punkt einer Parabel an einen Durchmesser eine Ordinate gezogen, und dieser Durchmesser über seinen Scheitel um ein ebenso grosses Stück, als zwischen dem Scheitel und der Ordinate liegt, verlängert wird, so ist die Verbindungslinie des so erhaltenen Punktes mit dem Parabelpunkt eine Tangente.
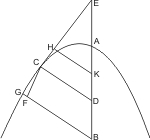 Sei eine Parabel mit dem Durchmesser AB gegeben, und von einem beliebigen Punkt C derselben die Ordinate CD gezogen, und DA um sich selbst verlängert bis zum Punkte E, so wird behauptet, dass EC eine Tangente sei. Wäre sie es nicht, so müsste entweder ihre Verlängerung CF innerhalb fallen, oder zwischen E und C ein Schneidungspunkt statt finden.
Sei eine Parabel mit dem Durchmesser AB gegeben, und von einem beliebigen Punkt C derselben die Ordinate CD gezogen, und DA um sich selbst verlängert bis zum Punkte E, so wird behauptet, dass EC eine Tangente sei. Wäre sie es nicht, so müsste entweder ihre Verlängerung CF innerhalb fallen, oder zwischen E und C ein Schneidungspunkt statt finden.
Fiele also erstens die Verlängerung von EC innerhalb, so sei F ein Punkt derselben und werde von F den Ordinaten parallel die Gerade FB bis zum Durchmesser gezogen, welche die Parabel in G trifft. Dann ist- GB2 : CD2 > FB2 : CD2
- BA : DA > BE2 : DE2
- 4 · BA · AE : 4 · DA · AE > BE2 : DE2,
Läge zweitens zwischen E und C ein Schneidungspunkt H mit der Parabel, so ziehe man die Ordinate HK, dann müsste, da CD2 : HK2 = DE2 : KE2 und auch CD2 : HK2 = DA : KA, also DE2 : KE2 = DA : KA, oder wenn man das zweite Verhältniss mit 4·AE erweitert: DE2 : KE2 = 4·AE · DA : 4·AE · KA, und da DE2 = 4·AE · DA, müsste auch KE2 = 4·AE · KA sein, was unmöglich ist, da A nicht die Mitte von KE ist.
Anm. Es ist übrigens leicht, diesem Beweis die indirekte Form zu nehmen, welche in der That nur scheinbar ist, da es darauf ankommt, direkt zu beweisen, dass FB < GB ist, Dies thut Viviani in seiner Divin. in quintum Apollonii.
Lehrsatz 34. Wenn auf einer Hyperbel oder Ellipse oder einem Kreisumfang ein Punkt angenommen und von ihm eine Ordinate gezogen wird, und wenn auf dem Durchmesser zu den beiden Endpunkten des latus tranaveraum und dem durch die Ordinate erhaltenen Punkt der letzterem zugeordnete vierte harmonische Punkt genommen wird, so ist die Verbindungslinie dieses Punktes mit dem zuerst auf dem Kegelschnitt angenommenen eine Tangente.
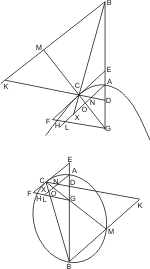 Sei eine Hyperbel oder eine Ellipse oder ein Kreisumfang mit dem Durchmesser AB gegeben, und auf dem Kegelschnitt ein Punkt C angenommen; ferner von C die Ordinate CD gezogen, und auf AB ein Punkt E so bestimmt, dass AE : BE = AD : BD ist, so wird behauptet, dass die Gerade CE den Kegelschnitt berühre.
Sei eine Hyperbel oder eine Ellipse oder ein Kreisumfang mit dem Durchmesser AB gegeben, und auf dem Kegelschnitt ein Punkt C angenommen; ferner von C die Ordinate CD gezogen, und auf AB ein Punkt E so bestimmt, dass AE : BE = AD : BD ist, so wird behauptet, dass die Gerade CE den Kegelschnitt berühre.
Wird also von einem andern Punkt F der Geraden EC die Linie FG parallel den Ordinaten nach dem Durchmesser hin gezogen, welche den Kegelschnitt in H schneidet, so ist zu beweisen: FG > HG.
Man ziehe von A und B die Linien AL, BK parallel mit EC, und die Gerade CG, bis sie die Parallelen in O, M trifft, so wie CB, bis sie AL in X schneidet, verlängere CD, bis sie AL in N, BM in K schneidet. Da nun AD : BD = AN :BK, AE : BE = CX : CB = XN : BK, nach Annahme aber AD : BD = AE : BE, ist AN : BK = XN : BK und also AN = NX. Mithin ist AN · NX > AO · OX oder AN : AO > OX : NX oder, da OX : NX = BM : BK, AN : AO > BM : BK d.h. AN · BK > BM · AO.
Nun ist aber wegen Aehnlichkeit der Dreiecke CDE, NDA und KDB
NA · BK : CE2 = AD · BD : DE2
und wegen Aehnlichkeit der Dreiecke CGE, OGA und MGB
OA · BM : CE2 = AG · BG : GE2, also
AD · BD : DE2 > AG · BG : GE2, oder, da DE2 : GE2 = DC2 : GF2, ist AD · BD : DC2 = AG ·BG : HG2, ist AG · BG : HG2 > AG · BG : GF2, und also FG > HG, und F ausserhalb des Kegelschnitts, was zu beweisen war.
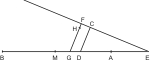 Anderer Beweis. Seien zwei Punkte G, D in einer begränzten Geraden AB angenommen, so dass DA < DB und GB > GA> DA, von ihnen Parallelen GH, DC gezogen, und in der verlängerten BA ein Punkt E bestimmt, so dass
Anderer Beweis. Seien zwei Punkte G, D in einer begränzten Geraden AB angenommen, so dass DA < DB und GB > GA> DA, von ihnen Parallelen GH, DC gezogen, und in der verlängerten BA ein Punkt E bestimmt, so dass
- GH2 : GA · GB = CD2 : DA · DB und
- AE : BE = AD : BD,
Bew. Da GF2 : CD2 = GE2 : DE2 und
GH2 : CD2 = AG · BG : AD · BD, bleibt zu zeigen
GE2 : DE2 > AG · BG : AD · BD.
Nun ist, wenn M die Mitte zwischen A und B ist, AD · BD = MA2 - MD2 = MD · ME - MD2 = M · DE, und AG · BG = MA2 - MG2. Setzt man dies ein, vertauscht die inneren Glieder und hebt mit DE, so erhält man:
GE2 : MA2 - MG2 > DE : MD, oder componendo GE2 + MA2 - MG2 : GE2 > ME : DE.
nun ist GE2 - MG2 = ME · (GE - MG) und MA2 = MD · ME, also eingesetzt und mit ME gehoben GE - MG + MD : GE2 > 1 : DE oder GE + GD : GE > GE :GE - GD, was einleuchtet. Mithin ist bewiesen, dass GE2 : DE2 > AG · BG : AD · BD und also auch, dass GF > GH.
Anm. Ein anderer Beweis findet sich in Viviani divinatio in V. conicorum Ap.
Lehrsatz 35. Wenn eine gerade Linie eine Parabel berührt und bis zu ihrem Durchschnittspunkt mit einem Durchmesser derselben verlängert wird, so wird die vom Berührungspunkt an den Durchmesser gezogene Ordinate auf diesem vom Scheitel an gerechnet ein ebenso grosses Stück abschneiden, als das zwischen dem Scheitel und dem Durchschnittspunkt mit der Tangente befindliche, und in den Raum zwischen der Tangente und dem Kegelschnitt kann vom Berührungspunkt aus keine zweite Gerade gezogen werden.
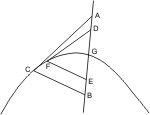 Sei eine Parabel mit dem Durchmesser AB gegeben, auf ihr ein Punkt C angenommen und in diesem eine Tangente CA und die Ordinate CB gezogen; ist nun G der Scheitel, so wird behauptet, dass AG = GB ist.
Sei eine Parabel mit dem Durchmesser AB gegeben, auf ihr ein Punkt C angenommen und in diesem eine Tangente CA und die Ordinate CB gezogen; ist nun G der Scheitel, so wird behauptet, dass AG = GB ist.
Wäre AG nicht gleich GB, so sei GE = AG und in E die Ordinate EF gezogen, dann wird die gerade Linie AF den Kegelschnitt in F berühren nach § 33 und also verlängert mit AC zusammen treffen müssen, also hätten die geraden Linien AC und AF zwei verschiedene Schneidungspunkte, was unmöglich ist. Also ist AG nicht ungleich GB. Ferner wird behauptet, dass in den Raum zwischen CA und dem Kegelschnitt keine andere gerade Linie von C aus gezogen werden kann. Denn wäre CD eine solche Gerade, so setze man GE = GD, ziehe in E die Ordinate EF, dann wird die Gerade DF den Kegelschnitt in F berühren, also ihre Verlängerung ausserhalb des Kegelschnitts liegen, und deshalb mit DC zusammentreffen müssen, also hätten die beiden Geraden DF, DC zwei verschiedene Schneidungspunkte, was unmöglich ist, mithin fällt in den Raum zwischen AC und dem Kegelschnitt keine andere gerade Linie.
Lehrsatz 36.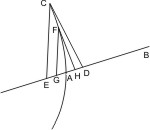 Wenn eine gerade Linie eine Hyperbel, Ellipse oder einen Kreisumfang berührt, und den verlängerten Querdurchmesser schneidet, und wenn vom Berührungspunkt an denselben Durchmesser eine Ordinate gezogen wird, so verhalten sich auf diesem die beiden Stücke von den Scheiteln des Kegelschnitts bis zum Durchschnittspunkt der Tangente ebenso wie die beiden Stücke vom Fusspunkt der Ordinate bis zu den Scheiteln in derselben Ordnung genommen; und in den Raum zwischen der Tangente und dem Kegelschnitt kann vom Berührungspunkt aus keine andere Gerade gezogen werden.
Wenn eine gerade Linie eine Hyperbel, Ellipse oder einen Kreisumfang berührt, und den verlängerten Querdurchmesser schneidet, und wenn vom Berührungspunkt an denselben Durchmesser eine Ordinate gezogen wird, so verhalten sich auf diesem die beiden Stücke von den Scheiteln des Kegelschnitts bis zum Durchschnittspunkt der Tangente ebenso wie die beiden Stücke vom Fusspunkt der Ordinate bis zu den Scheiteln in derselben Ordnung genommen; und in den Raum zwischen der Tangente und dem Kegelschnitt kann vom Berührungspunkt aus keine andere Gerade gezogen werden.
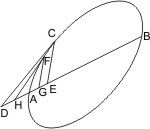 Sei eine Hyperbel oder eine Ellipse oder der Umfang eines Kreises mit dem Durchmesser AB gegeben, und im Punkte C derselben die Tangente CD und die Ordinate CE gezogen, so wird behauptet, dass AD : BD = AE : BE. Denn wäre das nicht der Fall, so sei AD : BD = AG : BG und in G die Ordinate GF gezogen, dann würde DF den Kegelschnitt in F berühren nach § 34 und deshalb verlängert mit DC zusammentreffen müssen, also hätten zwei gerade Linien zwei verschiedene Durchschnittspunkte, was unmöglich ist. Ferner wird behauptet, dass in den Raum zwischen dem Kegelschnitt und der Tangente CD von C aus keine andere gerade Linie gezogen werden könne.
Denn wäre z. B. CH eine solche, so nehme man den Punkt G dergestalt, dass AG : BG = AH : BH, und ziehe in G die Ordinate GF, dann würde HF nach § 34 den Kegelschnitt in F berühren und also, verlängert, mit HC zusammentreffen müssen, also hätten die beiden Geraden HC, HF zwei verschiedene Durchschnittspunkte, was unmöglich ist. Mithin lässt sich von C in den Raum zwischen dem Kegelschnitt und der Tangente CD keine andere gerade Linie ziehen.
Sei eine Hyperbel oder eine Ellipse oder der Umfang eines Kreises mit dem Durchmesser AB gegeben, und im Punkte C derselben die Tangente CD und die Ordinate CE gezogen, so wird behauptet, dass AD : BD = AE : BE. Denn wäre das nicht der Fall, so sei AD : BD = AG : BG und in G die Ordinate GF gezogen, dann würde DF den Kegelschnitt in F berühren nach § 34 und deshalb verlängert mit DC zusammentreffen müssen, also hätten zwei gerade Linien zwei verschiedene Durchschnittspunkte, was unmöglich ist. Ferner wird behauptet, dass in den Raum zwischen dem Kegelschnitt und der Tangente CD von C aus keine andere gerade Linie gezogen werden könne.
Denn wäre z. B. CH eine solche, so nehme man den Punkt G dergestalt, dass AG : BG = AH : BH, und ziehe in G die Ordinate GF, dann würde HF nach § 34 den Kegelschnitt in F berühren und also, verlängert, mit HC zusammentreffen müssen, also hätten die beiden Geraden HC, HF zwei verschiedene Durchschnittspunkte, was unmöglich ist. Mithin lässt sich von C in den Raum zwischen dem Kegelschnitt und der Tangente CD keine andere gerade Linie ziehen.
Lehrsatz 37. Wenn eine Tangente an einer Hyperbel, Ellipse oder einem Kreisumfang mit einem Durchmesser zusammentrifft, und von dem Berührungspunkte aus an diesen die Ordinate gezogen wird, so ist das Rechteck aus den beiden Abschnitten des Durchmessers vom Mittelpunkt des Kegelschnitts bis zu den Durchschnittspunkten der Tangente und Ordinate gleich dem Quadrat des halben latus transversum. Das Rechteck aber aus dem Abschnitt zwischen Mittelpunkt und Ordinate und dem zwischen Ordinate und Tangente hat zum Quadrat der Ordinate dasselbe Verhältniss als das latus transversum zum latus rectum.
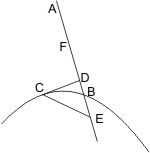 Ist eine Hyperbel, Ellipse oder ein Kreisumfang mit dem latus transversum AB und dem Centrum F gegeben, und von einem Punkt D derselben die Ordinate CE und die Tangente CD gezogen, so wird behauptet:
Ist eine Hyperbel, Ellipse oder ein Kreisumfang mit dem latus transversum AB und dem Centrum F gegeben, und von einem Punkt D derselben die Ordinate CE und die Tangente CD gezogen, so wird behauptet:
- FB2 = FD · FE,
- FE · ED = AE · BE. (siehe § 12 u. 13)
- AD : BD = AE : BE,
- AB : BD = AE ± BE : BE,
- FB : BD = FE : BE,
- FD : FB = FB : FE oder FB2 = FD · FE.
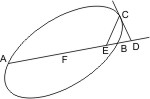 Addirt man in (3) die correspondirenden Glieder bei der Hyperbel oder subtrahirt sie bei Ellipse und Kreis, so erhält man:
Addirt man in (3) die correspondirenden Glieder bei der Hyperbel oder subtrahirt sie bei Ellipse und Kreis, so erhält man:
- AE : FE = DE : BE oder FE · DE = AE · BE.
Anm. des Uebers. Diese Sätze sind jetzt als Elementarsätze in der Lehre von den harmonischen Punkten hinreichend bekannt.
Anm. des Eutoc. Aus diesen letzten Sätzen erhellt, wie man von einem Punkt auf dem Durchmesser eines Kegelschnitts oder im Scheitel selbst eine Tangente an denselben ziehen kann.
Lehrsatz 38. Wenn an eine Hyperbel, Ellipse oder einen Kreisumfang eine Tangente, die mit dem weiten Durchmesser zusammentrifft, und vom Berührungspunkt nach diesem Durchmesser hin eine Parallele mit dem ersten Durchmesser gezogen wird, so ist das Rechteck aus den beiden Abschnitten auf dem zweiten Durchmesser vom Mittelpunkt des Kegelschnitts an bis zu der erwähnten Parallele und bis zu der Tangente, gleich dem Quadrat des halben zweiten Durchmessers; das Rechteck aber aus den beiden Abschnitten zwischen dem Mittelpunkt und jener Parallele und zwischen dieser Parallele und der Tangente verhält sich zu dem Quadrat der Parallelen wie das latus rectum zum latus transversum.
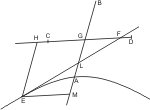 Sei eine Hyperbel oder Ellipse oder ein Kreisumfang mit dem Durchmesser AGB und dem zweiten Durchmesser CGD und eine Tangente ELF, die in E berührt, in L den ersten, in F den zweiten Durchmesser schneidet, gegeben, und von E parallel dem ersten Durchmesser die Linie BH bis zum zweiten Durchmesser gezogen, so wird, wenn r das latus rectum bedeutet, behauptet:
Sei eine Hyperbel oder Ellipse oder ein Kreisumfang mit dem Durchmesser AGB und dem zweiten Durchmesser CGD und eine Tangente ELF, die in E berührt, in L den ersten, in F den zweiten Durchmesser schneidet, gegeben, und von E parallel dem ersten Durchmesser die Linie BH bis zum zweiten Durchmesser gezogen, so wird, wenn r das latus rectum bedeutet, behauptet:
- GC2 = GF · GH,
- GH · HF : EH2 = r : AB.
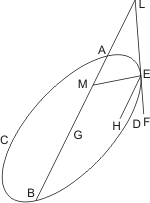 Beweis. Zieht man noch von E die Ordinate EM so ist
Beweis. Zieht man noch von E die Ordinate EM so ist
- EM2 : GM · LM = r : AB nach § 37.
- HG · GF : GM · GL = CG2 : AG2;
Anm. 1. Hieraus zeigt man leicht, dass die Endpunkte des zweiten Durchmessers, der Fusspunkt der Tangente und der vom Berührungspunkt aus auf denselben gezogenen Ordinate harmonische Punkte sind.
Anm. 2. Aus dem Gesagten erhellt, dass die Linie EF den Kegelschnitt berührt, wenn entweder das Rechteck FG · GH gleich dem Quadrat von GC oder wenn das Rechteck FH · BG zu dem Quadrat von HE sich wie das latus rectum zum latus transversnm verhält, welches beides indirekt leicht gezeigt werden kann.
Lehrsatz 39. Wenn eine Tangente an einer Hyperbel, Ellipse oder einem Kreisumfang den Durchmesser schneidet, und vom Berührungspunkt eine Ordinate gezogen wird, so hat zu einem jeden der beiden Abschnitte des Durchmessers, die zwischen der Ordinate und dem Mittelpunkt des Schnitts und zwischen der Ordinate und Tangente legen, die Ordinate ein Verhältniss, das zusammengesetzt ist aus dem Verhältniss des andern jener beiden Abschnitte zur Ordinate, und dem des latus rectum zum latus transversum.
 Der Apollonische Beweis ist folgender:
Der Apollonische Beweis ist folgender:
Sei AB das latus transversum eines Kegelschnitts mit dem Centrum F, und im Punkte C desselben die Ordinate CE, so wie die Tangente CD gezogen, und sei G eine Linie von der Beschaffenheit, dass FE · ED = CE · G oder G : FE = ED : CE ist, so hat man, da CE2 : FE · ED, also auch CE2 : CE · G, also CE : G = r : AB,- CE : G = r : AB,
- G : FE = ED : CE,
 Die Richtigkeit des Satzes erhellt übrigens unmittelbat aus § 37, da hiernach das Quadrat der Ordinate zum Rechteck aus den erwähnten beiden Abschnitten sich wie das latutus rectum zum latus tranaversum verhält, indem man nur einmal die Ordinate aus dem ersten Glied ins vierte und einen der beiden Abschnitte aus dem zweiten Glied ins dritte rückt, wodurch die Richtigkeit der Proportion nicht leidet.
Die Richtigkeit des Satzes erhellt übrigens unmittelbat aus § 37, da hiernach das Quadrat der Ordinate zum Rechteck aus den erwähnten beiden Abschnitten sich wie das latutus rectum zum latus tranaversum verhält, indem man nur einmal die Ordinate aus dem ersten Glied ins vierte und einen der beiden Abschnitte aus dem zweiten Glied ins dritte rückt, wodurch die Richtigkeit der Proportion nicht leidet.
Lehrsatz 40. Wenn eine Tangente an einer Hyerbel, Ellipse oder einem Kreisumfang den zweiten Durchmesser schneidet und vom Berührungspunkt an diesen Durchmesser eine Parallele mit dem andern Durchmesser gezogen wird, so wird einer der beiden Abschnitte auf dem zweiten Durchmesser, die zwischen dem der Parallelen und dem Mittelpunkt des Schnitts und zwischen derselben und der Tangente liegen, zu der Parallelen ein Verhältniss haben, das zusammengesetzt ist aus dem Verhältniss desjedesmaligen andern Abschnitts zur Parallelen und dem des latus transversum zum latus rectum.
Die Richtigkeit des Satz es erhellt auf dieselbe Weise aus § 38 als die des vorigen aus § 37.
Lehrsatz 41. Wenn in einer Hyperbel oder Ellipse oder einem Kreisumfang eine Ordinate gezogen wird und über der Ordinate und dem Halbmesser gleichwinklige Parallelogramme beschrieben werden, und die Ordinate zu der andern Seite des über ihr beschriebenen Parallelogramms ein Verhältniss hat, das zusammengesetzt ist aus dem Verhältniss des Halbmessers zu der andern Seite des über ihm beschriebenen Parallelogramms und dem des latus rectum zum latus transversum, und wenn noch ein Parallelogramm über dem Abschnitt des Durchmessers vom Mittelpunkt bis zur Ordinate, ähnlich dem über dem Halbmesser befindlichen, construirt wird, so ist bei der Hyperbel das über dem Halbmesser befindliche Parallelogramm gleich dem Unterschied zwischen dem zuletzt erhaltenen und dem über der Ordinate, bei Ellipse und Kreis aber gleich der Summe dieser selben Parallelogramme.
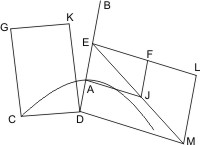 Sei eine Hyperbel mit dem latus transversum AB, dem Mittelpunkt E gegeben, von einem beliebigen Punkt C derselben die Ordinate CD gezogen und über EA ein beliebiges Parallelogramm EAIF, über CD aber damit ein gleichwinkliges CDKG construirt, so dass: CD : CG = EA · r : EF ·AB, wo r das latus rectum bedeutet; so wird behauptet, dass, wenn über ED ein mit AEFI ähnliches Parallelogramm DELM gezeichnet wird:
Sei eine Hyperbel mit dem latus transversum AB, dem Mittelpunkt E gegeben, von einem beliebigen Punkt C derselben die Ordinate CD gezogen und über EA ein beliebiges Parallelogramm EAIF, über CD aber damit ein gleichwinkliges CDKG construirt, so dass: CD : CG = EA · r : EF ·AB, wo r das latus rectum bedeutet; so wird behauptet, dass, wenn über ED ein mit AEFI ähnliches Parallelogramm DELM gezeichnet wird:
- AEFI = DELM - CDKG.
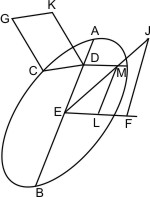
- CD : CG = CD2 · EA : (DE2 - EA2) · EF,
- CG · CD = (EF ⁄ EA) · DE2 - EF · EA
- CG · CD = EL · ED - EF · EA,
Auf ganz gleiche Weise erhält man bei gehöriger Aenderung der Zeichen bei der Ellipse- CG · CD = EF · EA - EL · ED.
Lehrsatz 42. Wenn eine Tangente einer Parabel den Durchmesser schneidet und vom Berührungspunkt eine Ordinate gezogen wird, von einem beliebigen Punkt des Kegelschnitts aber an den Durchmesser zwei Linien gezogen werden, von denen die eine der Tangente, die andere der Ordinate parallel ist, so ist das durch diese beide Linien entstandene Dreieck gleich dem Parallelogramm zwischen der Ordinate und dem Abschnitt des Durchmessers vom Scheitel bis zu der mit der Ordinate gezogenen Parallelen.
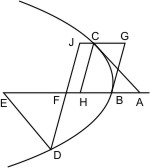 Sei eine Parabel mit dem Scheitel B und dem Durchmesser AB gegeben und in dem Punkt C derselben eine Tangente CA bis an den Durchmesser und die Ordinate CH gezogen, und werde ferner von einem beliebigen Punkt D der Parabel bis an den Durchmesser hin die Linie DF ∥ CH, und DE ∥ CA gezogen, so ist, wenn man noch das Parallelogramm CHB bis zum Punkt G vollendet, und den Durchschnittspunkt von DF mit GC I nennt: ⬜ ∆
Sei eine Parabel mit dem Scheitel B und dem Durchmesser AB gegeben und in dem Punkt C derselben eine Tangente CA bis an den Durchmesser und die Ordinate CH gezogen, und werde ferner von einem beliebigen Punkt D der Parabel bis an den Durchmesser hin die Linie DF ∥ CH, und DE ∥ CA gezogen, so ist, wenn man noch das Parallelogramm CHB bis zum Punkt G vollendet, und den Durchschnittspunkt von DF mit GC I nennt: ⬜ ∆
- ∆DFE = ⬜BGIF.
Lehrsatz 43. Wenn eine Tangente an einer Hyperbel, einer Ellipse oder einem Kreisumfang mit dem Durchmesser zusammentrifft, vom Berührungspunkt an den Durchmesser eine Ordinate, und hiermit eine Parallele vom Scheitel aus gezogen wird, bis sie die Verbindungslinie des Berührungspunktes mit dem Mittelpunkt schneidet; wenn ferner von einem beliebigen Punkt des Kegelschnitts nach dem Durchmesser hin zwei Linien gezogen werden, von denen die eine der Tangente, die andere der Ordinate parallel ist, so ist das durch diese beide Linien und den Durchmesser begrenzte Dreieck bei der Hyperbel gleich dem Dreieck, das von der zuletzt genannten Parallelen, dem Durchmesser und der Linie vom Mittelpunkt nach dem Berührungspunkt gebildet wird, vermindert um ein diesem ähnliches über dem Halbmesser beschriebenes Dreieck; bei der Ellipse und dem Kreis aber gleich demselben Unterschied mit verwechseltem Minuendus und Subtrahendus.
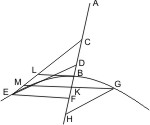 Sei eine Hyperbel oder eine Ellipse oder ein Kreisumfang mit dem Durchmesser AB und dem Centrum C gegeben, und in einem Punkt E des Schnitts die Tangente ED, die Ordinate EF, so wie im Scheitel B die Linie BL parallel EF gezogen, bis sie der Verbindungslinie CE in L begegnet; werden ferner von einem beliebigen Punkte G des Kegelschnitts an den Durchmesser hin GH ∥ ED und GK ∥ EF gezogen, letztere aber nöthigenfalls bis zu ihrem Durchschnitt M mit CE verlängert, so wird behauptet:
Sei eine Hyperbel oder eine Ellipse oder ein Kreisumfang mit dem Durchmesser AB und dem Centrum C gegeben, und in einem Punkt E des Schnitts die Tangente ED, die Ordinate EF, so wie im Scheitel B die Linie BL parallel EF gezogen, bis sie der Verbindungslinie CE in L begegnet; werden ferner von einem beliebigen Punkte G des Kegelschnitts an den Durchmesser hin GH ∥ ED und GK ∥ EF gezogen, letztere aber nöthigenfalls bis zu ihrem Durchschnitt M mit CE verlängert, so wird behauptet:
- ∆GHK = BKML.
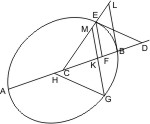 Bew. Nach § 39 ist das Verhältniss EF : FD zusammengesetzt aus dem Verhältniss CF : FE und dem Verhältniss des latus rectum zum latus transversum, da nun EF : FD = GK : KH und CF : FE = CB : LB, so ist das Verhältniss GK : KH zusammengesetzt aus dem Verhältniss CB : LB und dem Verhältnis des latus rectum zum latus transversum, weshalb, da auch ∠GKH und ∠CKM gleich sind oder sich zu 2 Rechten ergänzen, nach § 41 das doppelte Dreieck CKH bei der Hyperbel gleich dem doppelten Dreieck CKM, vermindert um das doppelte Dreieck CBL, und also auch GKH = LBMK ist; bei der Ellipse findet Aehnliches Statt.
Bew. Nach § 39 ist das Verhältniss EF : FD zusammengesetzt aus dem Verhältniss CF : FE und dem Verhältniss des latus rectum zum latus transversum, da nun EF : FD = GK : KH und CF : FE = CB : LB, so ist das Verhältniss GK : KH zusammengesetzt aus dem Verhältniss CB : LB und dem Verhältnis des latus rectum zum latus transversum, weshalb, da auch ∠GKH und ∠CKM gleich sind oder sich zu 2 Rechten ergänzen, nach § 41 das doppelte Dreieck CKH bei der Hyperbel gleich dem doppelten Dreieck CKM, vermindert um das doppelte Dreieck CBL, und also auch GKH = LBMK ist; bei der Ellipse findet Aehnliches Statt.
Anderer Beweis:- ∆CDE : ∆CEF = CD : CF,
- ∆CLB : ∆CEF = CB2 : CF2,
- ∆CDE = ∆CLB,
- ∆EDF = EFBL.
- ∆KHG = KG2 : EF2 = KB · KA : FB · FA = KC2 - BC2 : FC2 - BC2.
- KC2 - BC2 : FC2 - CB2 = ∆MKC - ∆LBC : ∆EFC : ∆LBC : = MKBL : EFBL, also
- ∆KHG : ∆EFD = MKBL : EFBL,
- ∆KGH = MKBL.
Lehrsatz 44. Wenn eine Tangente an einem von zwei Gegenschnitten den Durchmesser schneidet und im Berührungspunkt eine Ordinate gezogen wird, wenn ferner damit von dem Scheitel des andern Gegenschnitts eine Parallele gezogen wird, welche mit der Verbindungslinie des Mittelpunkts und des Berührungspunktes zusammentrifft, und wenn endlich von einem beliebigen Punkt des Kegelschnitts an den Durchmesser zwei Linien gezogen werden, deren eine der Tangente, die andere der Ordinate parallel ist, so ist das durch diese beiden Linien und den Durchmesser begrenzte Dreieck gleich dem von den zuletzt gezogenen Parallelen, dem Durchmesser und der Linie vom Mittelpunkt nach dem Berührungspunkt begrenzten Dreieck, vermindert um ein diesem ähnliches Dreieck über dem Halbmesser des Schnitts.
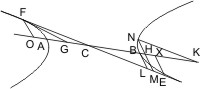 Seien zwei Gegenschnitte AF und BE mit dem Durchmesser AB und dem Mittelpunkt C gegeben, und von einem Punkt F in dem Schnitt FA die Ordinate FO und die Tangente FG bis an den Durchmesser gezogen, dann die Verbindungslinie FC verlängert, bis sie dem Gegenschnitt in E begegnet, durch den Scheitel B werde die Linie BL parallel FO bis zum Durchschnitt mit FE, und von einem beliebigen Punkt N des Gegenschnitts BE die Linie NK ∥ FG und NH ∥ FO, erstere bis an den Durchmesser, letztere nöthigenfalls verlängert bis zum Durchschnitt M mit FE, gezogen, so wird behauptet:
Seien zwei Gegenschnitte AF und BE mit dem Durchmesser AB und dem Mittelpunkt C gegeben, und von einem Punkt F in dem Schnitt FA die Ordinate FO und die Tangente FG bis an den Durchmesser gezogen, dann die Verbindungslinie FC verlängert, bis sie dem Gegenschnitt in E begegnet, durch den Scheitel B werde die Linie BL parallel FO bis zum Durchschnitt mit FE, und von einem beliebigen Punkt N des Gegenschnitts BE die Linie NK ∥ FG und NH ∥ FO, erstere bis an den Durchmesser, letztere nöthigenfalls verlängert bis zum Durchschnitt M mit FE, gezogen, so wird behauptet:
- ∆NHK = ∆CMH - ∆CBL.
Lehrsatz 45. Wenn von einem Punkt einer Hyperbel, Ellipse oder eines Kreises bis an den zweiten Durchmesser eine Tangente und eine Parallele mit dem ersten Durchmesser, so wie eine Linie nach dem Mittelpunkt, und von einem beliebigen andern Punkt des Kegelschnitts bis an den zweiten Durchmesser zwei Linien parallel mit jenen zuerst erwähnten gezogen werden, so ist das von diesen letzteren und dem zweiten Durchmesser gebildete Dreieck bei der Hyperbel gleich der Summe zweier Dreiecke, deren ersteres die Tangente zur Grundlinie und den Mittelpunkt zur Spitze hat, und deren anderes durch die vom zweiten Punkt mit dem ersten Durchmesser gezogene Parallele den zweiten Durchmesser und die Linie vom Berührungspunkt nach dem Mittelpunkt gebildet wird, bei der Ellipse und dem Kreis gleich dem Unterschied derselben Dreiecke in gleicher Ordnung genommen.
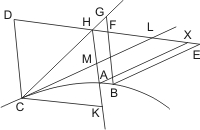 Sei eine Hyperbel oder Ellipse oder Umfang eines Kreises mit dem Durchmesser AH, dem zweiten Durchmesser HD, also dem Mittelpunkt H, gegeben, und von einem beliebigen Punkt C im Umfang die Tangente CL, die den ersten Durchmesser in M, den zweiten in L trifft, die Parallele CD mit dem ersten Durchmesser und die Linie CH, ferner von einem beliebigen zweiten Punkt B des Umfangs die Linie BE ∥ CL und BF ∥ CD gezogen, bis letztere CH in G schneidet, so wird behauptet, dass
Sei eine Hyperbel oder Ellipse oder Umfang eines Kreises mit dem Durchmesser AH, dem zweiten Durchmesser HD, also dem Mittelpunkt H, gegeben, und von einem beliebigen Punkt C im Umfang die Tangente CL, die den ersten Durchmesser in M, den zweiten in L trifft, die Parallele CD mit dem ersten Durchmesser und die Linie CH, ferner von einem beliebigen zweiten Punkt B des Umfangs die Linie BE ∥ CL und BF ∥ CD gezogen, bis letztere CH in G schneidet, so wird behauptet, dass
- bei der Hyperbel ∆BFE = ∆CHL + ∆GHF,
- bei Ellipse und Kreis ∆BFE = ∆CHL + ∆GHF.
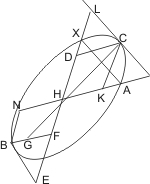 Man ziehe noch von C und B an den ersten Durchmesser die Ordinaten CK, BN und construire über AH das ∆AHX ähnlich mit ∆:CDL. Nach § 39 ist das Verhältniss von CK : KM, d. h. DL : CD, zusammengesetzt aus dem Verhältniss KH : CK und dem des latus rectum zum latus transversum, folglich wird nach § 41 das über der Ordinate CK construirte Parallelogramm CDHK bei der Hyperbel gleich dem über der Abscisse CD construirten, dessen Hälfte CDL ist, vermindert um ein dem letzteren ähnliches über dem Halbmesser AH, bei Ellipse und Kreis gleich demselben Unterschied in verkehrter Ordnung sein, also auch
Man ziehe noch von C und B an den ersten Durchmesser die Ordinaten CK, BN und construire über AH das ∆AHX ähnlich mit ∆:CDL. Nach § 39 ist das Verhältniss von CK : KM, d. h. DL : CD, zusammengesetzt aus dem Verhältniss KH : CK und dem des latus rectum zum latus transversum, folglich wird nach § 41 das über der Ordinate CK construirte Parallelogramm CDHK bei der Hyperbel gleich dem über der Abscisse CD construirten, dessen Hälfte CDL ist, vermindert um ein dem letzteren ähnliches über dem Halbmesser AH, bei Ellipse und Kreis gleich demselben Unterschied in verkehrter Ordnung sein, also auch
- ∆CHD = ∆CDL - ∆AHX bei Hyperbel,
- ∆CDH = ∆AHX - ∆CDL bei Ellipse.
- ∆CLH = ∆AHX.
- ∆CDH : ∆GFH = CK2 : BN2 = HK2 - HA2 : HN2 - HA2, und da
- HA2 : HN2 : HK2 = ∆HAX : ∆FBE : ∆DCL,
- ∆:CDH : ∆GFH = ∆DCL - ∆HAX : ∆FBE - ∆HAX,
- ∆GFH = ∆FBE - ∆HAX, oder nach 3): = ∆FBE - ∆CLH.
Lehrsatz 46. Wenn von einem Punkt einer Parabel eine Tangente und durch ihren Berührungspunkt eine Parallele mit dem Durchmesser gezogen wird, so halbirt diese letztere alle der Tangente parallelen Sehnen.
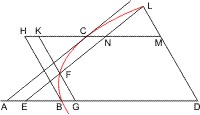 Sei eine Parabel mit dem Durchmesser ABD und im Punkte C derselben die Tangente CA, so wie die Parallele GM mit AB gegeben; wird nun von einem beliebigen Punkt L der Parabel eine Sehne LF parallel mit CA gezogen, so wird behauptet, dass diese durch GM in einem Punkt N halbirt werde.
Sei eine Parabel mit dem Durchmesser ABD und im Punkte C derselben die Tangente CA, so wie die Parallele GM mit AB gegeben; wird nun von einem beliebigen Punkt L der Parabel eine Sehne LF parallel mit CA gezogen, so wird behauptet, dass diese durch GM in einem Punkt N halbirt werde.
Man ziehe von L, F und dem Scheitel B die Ordinaten LD, FG, BH, bis sie GM in den Punkten M, K, H schneiden, verlängere noch LF, bis es in E den Durchmesser schneidet, so ist nach § 42- ∆LDE = ⬜BHMD,
- ∆FGE = ⬜BHKG,
Lehrsatz 47. Wenn von einem Punkt einer Hyperbel, Ellipse oder eines Kreisumfangs eine Tangente und ein Radius gezogen wird, so halbirt letzterer, nöthigenfalls verlängert, alle der Tangente parallelen Sehnen.
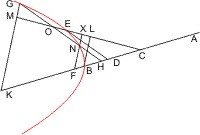 Sei eine Hyperbel oder eine Ellipse oder ein Kreisumfang mit dem Durchmesser AB, dem Scheitel B und dem Mittelpunkt C gegeben, und werde in einem beliebigen Punkt E des Umfangs eine Tangente ED bis an den Durchmesser und ein Radius EC, von einem andern beliebigen Punkt G des Umfangs aber eine mit ED parallele Sehne GN gezogen, so wird behauptet, dass GN von CE in einem Punkt 0 halbirt wird.
Sei eine Hyperbel oder eine Ellipse oder ein Kreisumfang mit dem Durchmesser AB, dem Scheitel B und dem Mittelpunkt C gegeben, und werde in einem beliebigen Punkt E des Umfangs eine Tangente ED bis an den Durchmesser und ein Radius EC, von einem andern beliebigen Punkt G des Umfangs aber eine mit ED parallele Sehne GN gezogen, so wird behauptet, dass GN von CE in einem Punkt 0 halbirt wird.
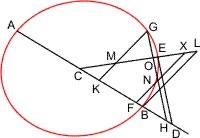 Man ziehe von G, N, B die Ordinaten GK, NF, BL, bis sie CE in den Punkten M, X, L schneiden, so ist nach § 43
und folglich ∆GOM = ∆NOX, da aber diese Dreiecke ähnlich sind, ist GO = ON. q. e. d.
Man ziehe von G, N, B die Ordinaten GK, NF, BL, bis sie CE in den Punkten M, X, L schneiden, so ist nach § 43
und folglich ∆GOM = ∆NOX, da aber diese Dreiecke ähnlich sind, ist GO = ON. q. e. d.- ∆GHK = BLMK,
- ∆NFH = BLXF,
Lehrsatz 48. Wenn von einem Punkt im Umfang eines von zwei Gegenschnitten eine Tangente und ein Radius gezogen werden, so halbirt letzterer in seiner Verlängerung alle im zweiten Gegenschnitt parallel mit der Tangente gezogenen Sehnen.
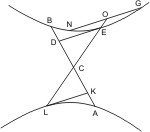 Seien zwei Gegenschnitte mit dem Durchmesser AB, dem Mittelpunkt C gegeben, und im Punkte L des einen von ihnen die Tangente LK und der Radius LC gezogen, so wird behauptet, dass die im andern Gegenschnitt parallel mit LK gezogene Sehne NG von der verlängerten LC in einem Punkt O halbirt wird. Man ziehe noch im Punkt E, wo die verlängerte LC den zweiten Gegenschnitt trifft, die Tangente ED, so ist nach dem, was in § 44 am Schluss gesagt ist, diese parallel mit LK, wodurch der Satz auf den vorigen zurückgebracht ist.
Seien zwei Gegenschnitte mit dem Durchmesser AB, dem Mittelpunkt C gegeben, und im Punkte L des einen von ihnen die Tangente LK und der Radius LC gezogen, so wird behauptet, dass die im andern Gegenschnitt parallel mit LK gezogene Sehne NG von der verlängerten LC in einem Punkt O halbirt wird. Man ziehe noch im Punkt E, wo die verlängerte LC den zweiten Gegenschnitt trifft, die Tangente ED, so ist nach dem, was in § 44 am Schluss gesagt ist, diese parallel mit LK, wodurch der Satz auf den vorigen zurückgebracht ist.
Lehrsatz 49. Wenn von einem beliebigen Punkt einer Parabel eine Tangente bis an einen Durchmesser und eine Parallele mit diesem, vom Scheitel aber den Ordinaten parallel eine Linie gezogen wird, und wenn, wie das Stück der Tangente zwischen dem Berührungspunkt und dieser letzten Parallelen, zu dem Stück der mit dem Durchmesser gezogenen Parallelen vom Berührungspunkt bis zu derselben Linie so eine neue Länge zur doppelten Tangente sich verhält, so ist das Quadrat einer von einem beliebigen Punkt der Parabel parallel mit der Tangente an die von ihrem Berührungspunkt ausgehende Parallele mit dem Durchmesser gezogene Linie gleich dem Rechteck des auf dieser dadurch abgeschnittenen Stückes und jener erwähnten neuen Länge, d. h. es ist für den vom Berührungspunkt ausgehenden Durchmesser diese neue Länge das zugehörige latus rectum.
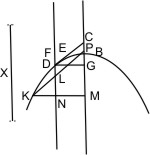 Sei eine Parabel mit dem Durchmesser CBM, dem Scheitel B gegeben, und werde im Punkte D derselben bis an den Durchmesser die Tangente DC, so wie die Parallele FDN mit dem Durchmesser, im Scheitel aber den Ordinaten parallel die Linie BEF gezogen, die die Tangente in E, die Parallele ND in F schneidet; sei nun DF : DE = 2 · CD : X, so wird, wenn von einem beliebigen Punkt K der Parabel bis an DN hin eine Parallele KL mit DC gezogen wird, behauptet:
Sei eine Parabel mit dem Durchmesser CBM, dem Scheitel B gegeben, und werde im Punkte D derselben bis an den Durchmesser die Tangente DC, so wie die Parallele FDN mit dem Durchmesser, im Scheitel aber den Ordinaten parallel die Linie BEF gezogen, die die Tangente in E, die Parallele ND in F schneidet; sei nun DF : DE = 2 · CD : X, so wird, wenn von einem beliebigen Punkt K der Parabel bis an DN hin eine Parallele KL mit DC gezogen wird, behauptet:
- KL2 = LD · X.
- ∆KPM = ⬜BFNM
- ∆KPM = NDCM;
- ∆KLN = LDCP.
Lehrsatz 50. Wenn eine Tangente an einer Hyperbel, Ellipse oder einem Kreise mit einem Durchmesser zusammentrifft, und vom Berührungspunkt eine Linie nach dem Mittelpunkt, vom Scheitel aus aber eine Ordinate bis zu dieser Verbindungslinie gezogen wird, und wenn, wie das Stück der Tangente zwischen dem Berührungspunkt und dieser Ordinate zu dem Stück der vom Mittelpunkt aus gezogenen Linie zwischen denselben Grenzen, so eine neue Länge sich zur doppelten Tangente verhält, so ist das Quadrat einer von einem beliebigen Punkt des Kegelschnitts aus parallel der Tangente bis an die Verbindungslinie des Mittelpunkts mit dem Berührungspunkt gezogenen Linie gleich dem Rechteck aus der vorerwähnten neuen Länge und dem Stück des Halbmessers zwischen dieser Linie, und dem Berührungspunkt bei der Hyperbel vermehrt um ein Rechteck von gleicher Breite, das ähnlich ist dem zwischen dem doppelten Halbmesser und der neuen Länge, bei der Ellipse um ein eben solches vermindert.
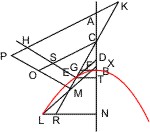 Sei eine Hyperbel oder Ellipse oder der Umfang eines Kreises mit dem Durchmesser AB und dem Mittelpunkt C gegeben, und im Punkte E an den Durchmesser hin die Tangente ED gezogen, die Verbindungslinie EC aber über C hinaus verdoppelt zum Punkt K, und nöthigenfalls auch über E verlängert, vom Scheitel B werde die Ordinate BFG, in E lotbrecht gegen EC die Linie EH, so dass FE : EG = EH : 2 · ED, ferner die Verbindungslinie HK gezogen. Nun ziehe man von einem beliebigen Punkt L des Kegelschnitts eine Linie LMX parallel der Tangente, die CE in M, CD in X trifft, und von L auch die Ordinate LN, die CE in R schneidet; endlich ziehe man von M eine Parallele mit EH, bis sie HK in P trifft, so wird behauptet:
Sei eine Hyperbel oder Ellipse oder der Umfang eines Kreises mit dem Durchmesser AB und dem Mittelpunkt C gegeben, und im Punkte E an den Durchmesser hin die Tangente ED gezogen, die Verbindungslinie EC aber über C hinaus verdoppelt zum Punkt K, und nöthigenfalls auch über E verlängert, vom Scheitel B werde die Ordinate BFG, in E lotbrecht gegen EC die Linie EH, so dass FE : EG = EH : 2 · ED, ferner die Verbindungslinie HK gezogen. Nun ziehe man von einem beliebigen Punkt L des Kegelschnitts eine Linie LMX parallel der Tangente, die CE in M, CD in X trifft, und von L auch die Ordinate LN, die CE in R schneidet; endlich ziehe man von M eine Parallele mit EH, bis sie HK in P trifft, so wird behauptet:
- LM2 = EM · MP.
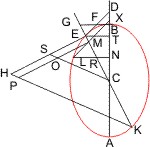 Beweis. Nach § 43 ist
Beweis. Nach § 43 ist
- ∆LNX = RNBG
- ∆LNX = RNDE,
- ∆ = EMXD,
- LM · MR = EM · [ED + MX],
- LM · ED = MR · ES,
- LM2 = EM ·(ES ⁄ ED) · [ED + MX];
- LM2 = EM · [ES + MO],
Lehrsatz 51. Wenn an einem von zwei Gegenschnitten eine Tangente gezogen wird, die den Durchmesser schneidet, vom Berührungspunkt nach dem Mittelpunkt eine gerade Linie gezogen und bis zum andern Gegenschnitt verlängert wird, im Scheitel des ersten aber eine Ordinate gezogen wird, und wenn, wie das Stück der Tangente zwischen dem Berührungspunkt und dieser Ordinate zu dem Stück der vom Mittelpunkt her gezogenen Linie zwischen denselben Grenzen, so eine neue Länge sich zur doppelten Tangente verhält, so ist das Quadrat einer Linie, die im andern Gegenschnitt parallel der Tangente bis an die vom Berührungspunkt durch den Mittelpunkt gehende Linie gezogen wird, gleich dem Rechteck aus dem durch sie darauf abgeschnittenen Stück und jener neuen Länge, vermehrt um ein Rechteck von gleicher Breite, das ähnlich ist dem aus dieser neuen Länge und dem zwischen beiden Gegenschnitten liegenden Stück der durch den Mittelpunkt gehenden Linie.
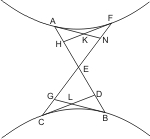 Seien zwei Gegenschnitte mit dem Durchmesser AB, dem Mittelpunkt E und im Punkte C des einen die Tangente CD gegeben, werde ferner die Linie CE gezogen und bis an den andern Gegenschnitt zum Punkt F verlängert; und im Scheitel B des ersten der beiden Gegenschnitte die Linie BLG den Ordinaten parallel gezogen, die CD in L, CE in G schneidet, und sei CL : CG = X : 2 · CD, wo X eine neue Länge ist, so ist klar, dass in dem Gegenschnitt BC das Quadrat einer von einem beliebigen Punkt des Schnitts an die verlängerte EG parallel mit CD gezogenen Linie gleich einem Rechteck aus X und dem durch eine solche Parallele auf EC gebildeten Abschnitt vermehrt um ein Rechteck von gleicher Breite ähnlich den zwischen X und CF enthaltenen ist. Es wird nun behauptet, dass dasselbe auch im andern Gegenschnitt AF statt findet.
Seien zwei Gegenschnitte mit dem Durchmesser AB, dem Mittelpunkt E und im Punkte C des einen die Tangente CD gegeben, werde ferner die Linie CE gezogen und bis an den andern Gegenschnitt zum Punkt F verlängert; und im Scheitel B des ersten der beiden Gegenschnitte die Linie BLG den Ordinaten parallel gezogen, die CD in L, CE in G schneidet, und sei CL : CG = X : 2 · CD, wo X eine neue Länge ist, so ist klar, dass in dem Gegenschnitt BC das Quadrat einer von einem beliebigen Punkt des Schnitts an die verlängerte EG parallel mit CD gezogenen Linie gleich einem Rechteck aus X und dem durch eine solche Parallele auf EC gebildeten Abschnitt vermehrt um ein Rechteck von gleicher Breite ähnlich den zwischen X und CF enthaltenen ist. Es wird nun behauptet, dass dasselbe auch im andern Gegenschnitt AF statt findet.
Man ziehe in F die Tangente FM und im Scheitel A den Ordinaten parallel AKN. Nun ist FM ∥ CD und FM = CD und da auch EF = EC, also überhaupt die zu beiden Seiten von E liegenden geradlinigen Figuren congruent sind, ist also FK : FN = X : 2 · FM, woraus die Behauptung erhellt.
Durch diese Lehrsätze ist nun gezeigt, dass in der Parabel eine jede Linie, die parallel mit dem aus der Erzeugung herrührenden Durchmesser gezogen wird, ein Durchmesser ist; in der Hyperbel aber, der Ellipse und den Gegenschnitten jede durch den Mittelpunkt gehende Linie; dass ferner fár jeden Durchmesser die Quadrate der parallel mit der Tangente im Scheitel gezogenen Ordinaten bei der Parabel gleich den daran liegenden Rechtecken [aus Abscisse und latus rectum] sind, bei der Hyperbel und den Gegenschnitten gleich diesen Rechtecken vermehrt um eine gewisse Figur und bei der Ellipse vermindert um dieselbe Figur; endlich folgt hieraus, dass, was für die aus der Erzeugung herrührenden Durchmesser bewiesen ist, auch gelte für beliebige andere Durchmesser.
- Weitere Seiten
- Einleitung
- Inhalt
- Erstes Buch
- Zweites Buch
- Drittes Buch
- Ellipse bei Apollonius