The General Use of the Canon and Tables of Logarithms.

CHAP. III.
Concerning the joynt Use of the Lines of Numbers, Sines and Tangents.

Concerning the joynt Use of the Lines of Numbers, Sines, and Tangents, I shewed how they might serve for the Resolution of Right-lined Triangles, whereof I set down five Propositions in the nineth Chapter of the first Book of the Croß-staff. And these also may be applied to the Table and Canon of Logarithms.

The Sides of these Triangles are measured by absolute Numbers, and so represented by Logarithms.

The Angles are measured by degrees and minutes, and so to be found by Sines and Tangents in the Canon.

PROP. I.
Having three Angles and one Side, to find the other two Sides.

If it be a Rectangle Triangle, wherein one Side about the right Angle bein known, it were required only to find the other, this might be readily done by Sines and Tangents. As in the Rectangle AIB, knowing the Angle BAI to be 43 gr. 20 m. and the Side AI to be 244, if it were required to find the other Side BI.

As the Radius (the Tangent of)		45 gr.	00 m.	10.0000000

Is to the Tangent of the Angle		43	30	9.9749195
So is the Side given	AI	244	⁰⁰⁰	2.3873898

To the Side required	BI	230	²⁰²	12.3611093

But where both the other Sides are required, it is best done by Logarithms and Sines. As in the same Rectangle AIB, having the three Angles and the Side AI, to find both BI and AB.

As the Sine of the opposite Angle	ABI	46	40	9.8617575
Is to the Side given	AI	244	⁰⁰⁰	2.3873898

				7.4743676

So is the Sine of the second Angle	BAI	43	20	9.8364770
To his opposite Side	BI	230	²⁰²	2.3621098

And the Sine of the third Angle	BAI	90	00	10.0000000
To his opposite Side	AB	335	⁵⁴³	2.5256323

The like holdeth also in Oblique-angled Triangles.

As in the Triangle ABD (which I proposed formerly as an example for the finding the Distances) where knowing the Distance between A and D, to be 100 paces; the Angle BAC to be 43 gr. 20 m. the Angle BDA 122, or the outward Angle BDC 58 gr. and consequently the Angle ABD opposite to AD the Side given, to be 140 gr. 40 m. it was required to find the Distances AB and DB.

As the Sine of the opposite Angle	ABD	14	40	9.4034544
Is to the Side given	AD	100	⁰⁰⁰	2.0000000

				7.4034554

So the Sine of the second Angle	ADB	58	00	9.9284204
To his opposite Side	AB	334	⁹¹⁷	2.5249650

And the Sine of the third Angle	DAB	43	26	9.8364770
To his opposite Side	DB	271	⁰¹²	2.4330216

PROP. II.
Having two Sides and one Angle opposite to either of those Sides, to find the other two Angles and the third Side.

As in the Triangle ABD, having the two Sides AB 335 paces; and AD 100 paces, and knowing the Angle ADB to be 58 gr. if it were required to find the other two Angles at A and B, and the third Side BD, I may first find an Angle ABD opposite to the other known Side AD.

As the opposite Side	AB	335	⁰⁰	2.5250448
To the Sine of the Angle given	ADB	58	00	9.9284204

				7.4033756

So is the next Side	AD	100	⁰⁰⁰	2.0000000
To the Sine of his opposite Angle	ABD	14	59 ⁵/₆	9.4033756

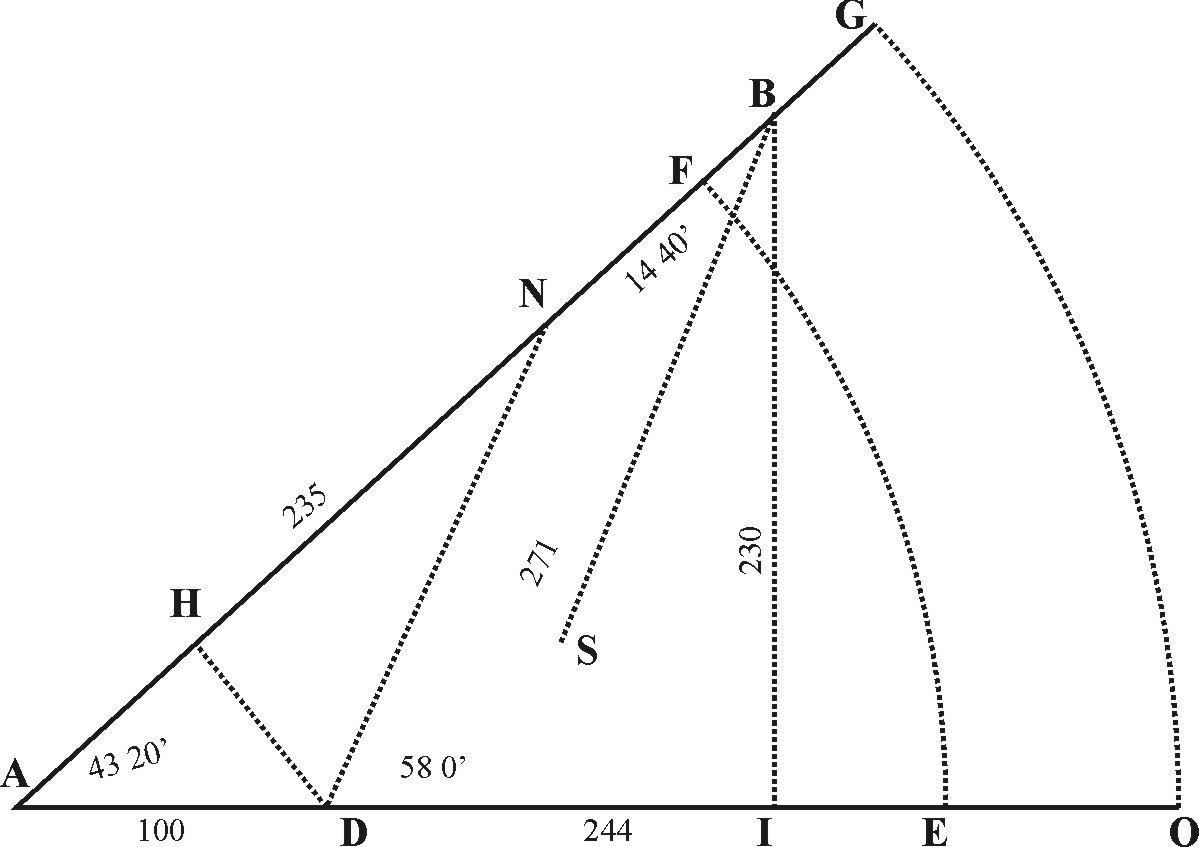
Then knowing these two Angles at D and B, I take the inward Angle ABD 14 gr. 59 m. 50 sec. out of the outward Angle BDC 58 gr. 00 m. and so find the third Angle BAD, to be 43 gr. 20 m. 10 sec. So having three Angles and two Sides I may well find the third Side BD by the former proportion.

As the Sine of the first Angle	ADB	58	00	9.9184102
To the opposite Side	AB	335	⁰⁰	2.5250448

				7.4033756

So the Sine of the last Angle	DAB	43	20 ¹/₆	9.8365043
To his opposite Side	DB	271	¹²²	2.4331277

PROP. III.
Having two Sides, and the Angle between them, to find the other two Angles and the third Side.

If the Angle conteined between the two Sides given be a right Angle, the other two Angles will be found readily by Tangents and Logarithms. As in the rectangle AIB having the Side AI 244, and the Side IB, to find the Angles at A and B.

As the greater Side	AI	244		2.3873898

Is to the lesser Side	IB	230		2.3617178
So the Radius, the Tangent of		43	18 ½	9.9743380

But if it be an oblique Angle that is conteined between the two Sides given, the Triangel may be reduced into two Rectangle Triangles, and then resolved as before.

As in the Triangle ADB, having the Sied AB 335, AC 100, and the Angle BAD 43 20', to find the Angles at B and D, and the third Side BD. First, I would suppose a Perpendicular DH to be let down from D, the end of the lesser Side, upon the greater Side AB: so shall I have two Rectangled Triangles DHA and DHB. And in the Rectangle AHD, the Angle at A being 43 20', the other Angle ADH will be 46 40' by Complement, and with these Angles and the Side AD, I may find both AH and DH by the first Proposition. Then taking AH out of AB, there remains HB for the Side of the rectangle DHB, and therefore with this Side HB and the other DH, I may find the Angle at B, by the former part of this Proposition. And with this Angle and the Perpendicular DH, I may find the third Side DB, by the first Proposition.

Or having two Sides and the Angle between them, we may find the other two Angles without letting down any Perpendicular, in this manner.

As the Sum of the two Sides given, Is to the Difference of these Sides:
So the tangent of the half the Sum of the two opposite Angles, To the Tangent of half of the Difference between those Angles.

So here having the Side	AB	335
and the other Side	AD	100

The Sum of these Sides is		435		2.6384892
and the Difference of these Sides		235		2.3719678

The Angle conteined BAD is		43	20	2674214
The Sum of the two opposite Angles		136	40
The Half Sum of these Angles		68	20	10.4009092
And by Proportion and half difference		53	40 ¹/₅	10.1334878

This half Sum and half Difference make 12 20 ¹/₃ the greater Angle and the Difference between them 14 19 ²/₃ the lesser Angle.

PROP. IV.
Having three Sides, to find the three Angles.

let one of the three Side given be the Base (but rather the greater Side) that the perpendicular may fall within the Triangle. Then gather the Sum and the Difference of the two Sides, and the Proportion will hold.

As the base of the Triangle, To the Sum of the Sides:
So the Difference of the Sides, To the alternate Base.

This alternate Base being taken forth of the true Base, if we let down a Perpendicular from the opposite Angle, it shall fall upon the middle of the Remainder. As in the Triangle ADB,

The lesser Side	AD	106
The other Side	BD	271

The Base of the Triangle	AB	335		2.5250448
The Sum of the Sides		371		2.5693739

				443291

The Difference of these Sides		171		2.232996
And so the alternate Base is		189	¹³⁶	2.2773152
This taken out of 335 leaves		145	⁶¹⁴
The half whereof is		72	⁸¹²

And such is the Segment AH, the Distance between the Angle at A, and the perpendicular DH. So that having drawn this Perpendicular, we have two Rectangle Triangles DHA and DHB, in which having two Sides, and the right Angle, we may find the other Angles by the second Proposition.

These four Propositions may suffice for the resolution of the Sides and Angles in all right-lined Triangles.

PROP. V.
Having the Base and Perpendicular in a right-lined Triangle, to find the superficial Content.

The Perpendicular may be found by one of the former Propositions, and that being known we may find the superficial Content. As in the Triangle ADB, having the Base AB 335, and the Perpendicular DH 68545.

As the Number of	2		0.3010700
To the Perpendicular	68.545		1.8359757

			1.5349457

So the Base	335		2.5250448
To the Content	11481	³⁹³	4.0599905

Or if we would find the Content without knowing the perpendicular, we may put two more Operations into one, as in the proportion following.

PROP. VI.
Having two Sides of a right-lined Triangle, and the Angle between them, to find the Content.

Add the Sine of the Angle, and the Logarithms of both the Sides, from the Sum of these subtract -10.3010300, so the Remainder shall be the Logarithm of the Content.

As in the Triangle ADB, having the Sides AB 335, AD 100, and the Angle BAD 43 gr. 20 m.

The Sine of the Angle		43 gr. 20 m. is	9.8364770
The Logarithm of the Side	AB	335	2.5250448
The Logarithm of the Side	AD	100	2.0000000

The Sum of these make			14.3615218

From this subtract the solemn Logarithm			10.3010300

The Remainder will be			4.0604918

The Logarithm of 11494 the Content required.

PROP. VII.
Having three Angles, and one Side of a right-lined Triangle, to find the Content.

Add the double of the Logarithm of the Side given, and the Sines of the two next Angles: from the Summ of these subtract the Sum of 10.3010300, and the Sine of the opposite Angle, so the Remainder shall be the Logarithm of the Content.

As in the Triangle ADB supposing the Angles BAC to be 34 gr. 20 m. BDA 127 gr. 00 m. ABD 14 gr. 40 m. and the Side AD to be 100 parts.

The Logarithm of the Side AC	100	is	2.0000000
The same again			2.0000000
The Sine of the Angle BAC	43	20	9.8364770
The Sine of the Angle BDA	58	90	9.9284104

The Sum of these four make			23.7648974

Again, if we add the solemn Logarithm			10.3010300
To the Sine of the opposite Angle	14	40	9.4034554

The Sum of both will make			19.7044854
Which subtracted from 23.7648974 leave			4.0604120

The Logarithm of 11492 the Content required.

PROP. VIII.
Having three Sides of a right-lined Triangle, to find the Content.

First, set down the three Sides, the Sum of them, and the Half-Sum. Then from this Half-Sum subtract each Side severally and note the Differences. That done, add the Logarithms of the Half-Sum, and these Differences, the half thereof shall be the Logarithm of the Content.

Thus in the Trangle ADB, the three Sides are	AB	335
	DB	271
	AD	100

The Sum of these Sides is		706

The Half-Sum		352	3.5477747
The Difference from	AB	18	1.2552725
The Difference from	DB	82	1.9138138
The Difference from	AD	253	2.4031205

The Sum of their Logarithms			8.1199815
And the half thereof is			4.0599907

The Logarithm of 11481²⁹³ the Content required.

PROP. IX.
Having three Sides of a right-lined Triangle, to find the Perpendicular.

As in the former Traingle ADB, to find the Perpendicular DH. First, find the Content of the Triangle by the former Proportion, then may the perpendicular be found by the converse of the fifth Proposition.

As the Base of the Triangel	335	2.5250448
To the Superficial Content	11481²⁹³	4.0599907

		1.5349459

So always the Number of	2	0.3010300
To the Perpendicular	68¹⁴¹	1.8359759

PROP. X.
Having the Semidiameter of a Circle, to find a Chord for any Ark proposed.

As if in protracting the former Triangle ADB, it were required to find the length of a Chord 43 gr. 20 m. agreeing to the Semidiameter AE, which we suppose to be three inches. This might be done by the first Proportion, for if the Chord were drawn from E to F we should have a Triangle EAF of three Angles and two Sides known. But, more generally comparing the Sine of 30 gr. with the Sine of half the Ark proposed, the Proportion will hold.

As the Sine of the Semi-radius	30 gr. 00 m.	9.6989700
To the Semidiameter	3⁰⁰⁰	0.4771212

		9.2218488

So the Sine of half the Ark	21 gr. 40 m.	9.5672689
To the Chord required	2²¹⁵	0.3454201

So that having drawn the Line AE, and described an occult Ark of a Circle upon the Center A, and the Semidiameter AE, at the Distance of three inches, if we take out two inches, and 215 parts of 1000, and inscribe them into that Ark from E to F, the line AF shall make the Angle FAE to be 43 gr. 20 m. as was required.

Thus having applied that to the Canon and Tables of Logarithms which I had set down before for the general Unse of the Lines of Numbers, Sines and Tangents, it may appear sufficiently, that, if we observe the Rules of Proportion set forth by others, and work by these Tables, we may use Addition instead of their Multiplication, and Subtraction instead of their Division, and so apply these general Rules to infinite particulars.

Zurück zum Inhaltsverzeichnis

Nächstes Kapitel