The First Book of the Cross-Staff
CHAPT. II. The Use of the Line of Inches for perpendicular heights and distances
In taking of heights and distances, the Staff may be held in such sort, that it may be even with the distance, and the Cross parallel with the height: and than with the eye at the beginning of the Staff shall see his marks by the inward sides of the two inward sights, there will be such proportion between the distance and the height, as is between the parts intercepted on the Staff and the Cross. Which may be further explaines in these Propositions.
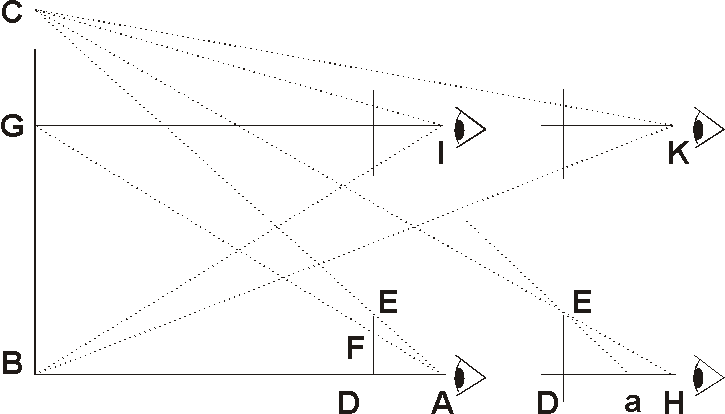
- To find an height at one Station, by knowing the distance
Set the middle height unto the distance upon the Staff, the height will be found on the Cross. For,
- As the segment of the Staff, unto the segment on the Cross,
- So is the distance given unto the height.
As if the distance AB being known to be 256 feet, it were required to find the heigth BC: first I place the middle sight at 25 inches and 6 parts of 10; then holding the Staff level with the distance, I raise the Cross Parallel uto the height, in such sort, as that my eye may see from A the beginning of the inches on the Staff by the sight E, at the beginning of the inches on the Cross unto the mark C: which being done; if I find 19 inches and 2 parts of 10 intercepted on the Cross between the sights at E and D, I would say the height BC were 192 feet.
Or if the observation were to be made before the distance were measured, I would set the middle sight either unto 10 inches, or 12, or 16, or 20, or 24, or some such number as might best be divided into several parts, and than work by proportion. As if in the former example the middle sight were at 24 on the Staff, and 18 on the Cross, it should seem that the height is 3/4 of the distance, and therefore the distance being 256 feet, the height should be 192.
- To find the height by knowing some part of the same height.
As if the height from G to C were known to be 48, and it were required to find the whole height BC, either put the third sight, or some other running sight upon the Cross between the eye and the mark G. For then,
- As the difference between the sights uto the whole segment of the Cross,
- So is the part of the height given, unto the whole height.
If then the difference between the sights at E and F, shall be 45, and the segment on the Cross ED 180, the whole height BC will be found to be 192.
- To find an height at two stations, by knowing the difference of the same stations.
- As the difference of Segments on the Staff, unto the diference of stations,
- So is the Segment of the Cross, unto the height.
Suppose the first station being at H, the Segment of the Cross ED were 180, and the segment of the Staff HD 300; then coming 64 feet nearer unto B, in a dirct Line unto a second station at A, and making another observation, suppose the segment of the Cross ED were 180 as before, and the segment of the Staff AD 240; take 240 out of 300, the difference of the segments will be 60 parts, and
- As 60 parts unto 64 the difference of the stations:
- So DE 180 unto BC 192 the height required.
In these three Propositions is a regard to be had of the height of the eye. For the height measured, is no more than from the level of the eye upward.
- To find a distance, by knowing the height.
- As the Segment of the Cross, so the Segment of the Staff:
- So the height given, unto the distance.
So the Segment ED being 18, and DA 24, the height CB 192, will shew the distance AB to be 256.
- To find a distance, by knowing part of the height.
- As the difference between the sights, unto the Segment of the Staff:
- So ist the part of the height given, unto the distance.
And thus the difference between E and F being 45, and the Segment DA 240; the part of the height GC, will give the distance AB to be 256.
- To find a distance at two stations, by knowing the difference of the same stations.
- As the difference of Segments on the Staff, unto the difference of stations:
- So is the whole Segment, unto the distance.
And thus the Segment of the Cross being 180, the Segment of the Staff at the first station 240, at the second 300, the difference of the Segments 60, and the difference of Stations 64, the distance AB at the first station will be found to be 256, and the distance HB at the second station 320.
- To find a breadth, by knowing the distance perpendicular to the breadth.
This is all one with the first Proposition. For this breadth is but an height turned sideways; and therefore:
- As the Segment of the Staff, unto the Segment of the Cross;
- So is the distance unto the breadth.
And thus the Segment of the Staff being 24, and the Segment of the Cross 18, the distance AB 256, will give the bradth BC to be 192.
- To find a breadth at two stations in a Line perpenducular to the breadth, by knowing the difference of the same stations.
This is also the same as the third Prop., and therefore
- As the difference of the Segments on the Staff, unto the difference of stations;
- So the Segment on the Cross between the two sights, unto the breadth required.
And thus the difference between the stations at A and H being 64, the difference of Segments on the Staff 60, the Segment on the Cross 180, the breadth BC will be found to be 192.
In like manner may we find the breadth GC, for having found the breadth BC, the proportions will hold;
- As DE is unto FE, so BC is unto GC. Or Otherwise,
- As H unto HA, so FE unto GC.
Neither is it material whether the two stations be chosen at one end of the breadth proposed, or without it, or within it, if the Line between the stations be Perpendicular unto the breadth; as may appear, if in stead of the stations at A and H, we make choice of the like stations at I and K.
There might be other ways proposed to work these Proportions, by holding the Cross even with the distance, and the Staff parallel with the height; but these would prove more troublesome , and those which are delivered are sufficient, and the same with those which others have set down under the name of the Jacobs Staff.