The First Book of the Cross-Staff

CHAPT. IX. The use of the Line of Sines and Tangents joyned with the Line of Numbers.

The Lines of Sines and Tangents have another like use joyned with the Line of Numbers, especially in the resolution of right Lined Triangles, where the Angles are measured by degrees and minutes, and the sides measured by absolute Numbers, whereof, I will set down these Propositions.

1. Having three Angles and one side, to find the other two sides.

If it be a Rectangle Triangle, wherein one side about the right Angle being known, it were required to find the other. This may be found by the Line of Tangents, and Line of Numbers. For,

• As the Tangent of 45 gr. to the Tangent of the Angle opposite to the side required;
• So the Number belonging to the side given, to the Number belonging to the side required.

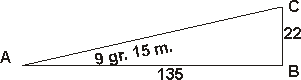
As in the Rectangle ABC, knowing the Angle CAB to be 9 gr. 15 m. and the side AB to be 135 parts, if it were required to find the other side BC about the right Angle.

Extend the Compasses from the Tangent 45 gr. unto the Tangent of 9 gr. 15 m., the same extent will reach in the Line of Numbers from 135 unto 22, and such is the length of the side BC. Or in the cross work, extend the Compasses from the Tangent of 45 gr. unto 135 in the Line of Numbers, the same extent will reach from the Tangent of 9 gr. 15 m. unto 22 in the Line of Numbers.

If this extent from the Tangent of 45 gr. to 9 gr. 15 m. or, 135 parts, be too large for the Compasses, you may use the Tangent of 5 gr. 43 m. instead of the Tangent of 45 gr. because both alike answer to 10 &c. parts in the Line of Numbers. And then either extend the Compasses from 5 gr. 43 m. unto 9 gr. 15 m. in the Line of Tangents, the same extent will reach from 135 unro 22 in the Line of Numbers: or else extend them from the Tangent of 5 gr. 43 m. unto 135 in the Line of Numbers, the same extent will reach from the Tangent of 9 gr. 15 m. unto 22 in the Line of Numbers, as before.

In like manner, in the same Rectangle ABC, knowing the Angle ACB to be 80 gr. 45 m. and the side BC to be 22 parts, it were required to find the other side BA. You may use the Tangent of 84 gr. 17 m. instead of the Tangent of 45 gr. and so the side BA will be found to be 135 parts.

This holdeth for finding of the sides of Rectangle Triangles, but generally in all Triangles, whether they be right or obtuse Angles, having three Angles and one side, we may find the two other sides by the Lines of Sines and the Line of Numbers.

• As the Sine of an Angle opposite to the side given, is to the Number belonging to that side given;
• So the Sine of the Angle opposite to the side required, to the Number belonging to the side required.

As in the example of the fourth Chapter of this Book, where knowing the distance between two stations A and B to be 100 paces, the Angle BAC to be 43 gr. 20 m. and the Angle BDC to be 58 gr. it was required to find the distance AB.

First, having these two Angles, I may find the third Angle ABD to be 14 gr. 40 m. either by subtraction or by Complement unto 180. Then in the Triangle BAD, I have three Angles, and one side, whereby I may find both AB and DB.

I know the Angle ABD opposite to the measured side AD, to be 14 gr. 40 m. wherefore I extend the Compasses in the Line of Sines, from 14 gr. 40 m. unto 122 gr. or (which is all one) to 58 gr. (for after 90 gr. the Sine 80 gr. is also the Sine of 100 gr. and the Sine of 70 gr. the Sine of 110 gr. and so in the rest) so shall I find the same extent to reach in the Line of Numbers, from 100 unto 335. And such is the distance required between A and B.

In the like manner I extend my Compasses from the Sine of 14 gr. 40 m. to the Sine of 43 gr. 20 m. the same extent will reach in the Line of Numbers from 100 to 271. And such is the distance between D and B.

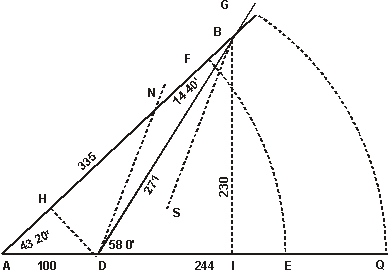
Or in cross work, I may extend the Compasses from 14 gr. 40 m. in the Sines, unto 100 parts in the Line of Numbers, so the same extent will give the distance from 58 gr. unto 335 parts, and from 43 gr. 20 m. to 271 parts.

2. Having two sides given, and one Angle opposite to either of these sides, to find the other two Angles and the third side.

• As the side opposite to the Angle given, is to the Sine of the Angle given:
• So the other side given, to the Sine of that Angle to which it is opposite.

So the former Triangle, having the two sides, AB 335 paces, and AD 100 paces, and knowing the Angle ADB, which is opposite to the side AB, to 122 gr. I may find the Angle ABD, which is opposite to the other side AD. For if I extend the Compasses from 335 unto 100 in the Line of Numbers, I shall find the same extent to reach in the Line of Sines from 122 gr. to 14 gr. 40 m. and therefore such is the Angle ABD.

Then knowing these two Angles ABD and ADB, I may find the third Angle BAD either by subtraction or by Complement to 180, to be 43 gr. 20 m. and having three Angles and two sides, I may well find the third side DB, by the former Proposition.

This may be done more readily by cross work, For if I extend the Compasses from 335 parts, in the Line of Numbers, to the Sine of 122 gr. the same extent will reach from 100 parts to the Sine of 14 gr. 46 m. and back from 43 gr. 20 m. to 271 parts; and such is the third side DE.

3. Having two sides and the Angle between them, to find the two other Angles and the third side.

If the Angle contained between the two sides be a right Angle, the other two Angles will be found readily by this Canon.

• As the greater side given, is to the lesser side:
• So is the Tangent of 45 gr. to the Tangent of the lesser Angle.

So in the Rectangle triangle, AIB, knowing the side AI to be 244, and the side IB 230: if I extend the Compasses from 244 to 230 in the Line of Numbers, the same extent will reach from 45 gr. to about 43 gr. 20 m. in the Line of tangents; and such is the lesser Angle BAI, and the Complement 46 gr. 40 m. shews the greater Angle ABI. The Angles being known, the third side AB may be found by the first Proposition.

So likewise in the example of the third Chapter of this Book, concerning taking Angles by the Line of Inches, where the parts intercepted on the Staff being 20 Inches, and the parts on the Cross 9 Inches, it was required to find the Angle of the Altitude. For,

I may extend the Compasses in the Line of Numbers, from 20 unto 9, the same extent will reach in the Line of Tangents from 45 gr. to 24 gr. 14 m.

Or in cross work,

I may extend the Compasses from 20 parts in the Line of Numbers, to the Tangent of 45 gr. the same extent shall give the distance from 9 parts, unto the Tangent of 24 gr. 14 m.

And such is the Altitude required.

If the parts intercepted on the Staff being 20 Inches, and the parts on the Cross 9 tenth parts of an inch, it were required to find the Angle of the Altitude. Here the Angle would be much less, and the 9 would fall out of the Line of Numbers.

To supply this defect, I use the Tangent of 5 gr. 43 m. instead of the Tangent of 45 gr.. And then if I extend the Compasses in the Line of Numbers from 20 unto 9, the same extent will reach in the Line of Tangents from 5 gr. 43 m. unto 2 gr. 35 m.

Or in cross work, if I extend them from 20 parts in the Line of Numbers, unto the Tangent of 5 gr. 43 m. the same extent will give the distance from 9 in the Line of Numebers, unto the Tangent of 2 gr. 35 m.

And such is this Angle of the Altitude required.

But if it be an oblique Angle thatis contained between the two sides given, the Triangle may be reduced into two Rectangle Triangles, and then resolved as before.

As if the Triangle ADB, where the side AB is 335, and the side AD 100, and the Angle BAD 43 gr. 20 m. If I let down the Perpendicular, DH upon the side AB, I shall have two Rectangle Triangles, AHD, DHB; and in the Rectangle AHD, the Angle at A being 43 gr. 20 m. the other Angle ADH will be 46 gr. 40 m. and with these Angles and the side AD, I may find both AH ans DH, by the first Proposition.

Or I may find the Angles required, without setting down any Perpendicular. For,

• As the sum of the sides, is to the difference of the sides:
• So is the Tangent of the half sum of the opposite Angels, to the tangent of half the difference between those Angles.

As in the former Triangle ADB, the sum of the sides AB, AD, is 435, and the difference between them 235; the Angle contained 43 gr. 20 m. and therefore the sum of the two opposite Angles 136 gr. 40 m. and the half sum 68 gr. 20 m. Hereupon I extend the Compasses in the Line of Numbers from 435 to 235, and find them to reach in the Lines of Tangents from 68 gr. 20 m. unto 53 gr. 40 m. and such is the half difference between the opposite Angles at B and D. This half difference being added to the half sum, doth give 122 gr. for the greater Angle ADB: and being subtracted, it leaveth 14 gr. 40 m. for the lesser Angle ABD, then the three Angles being known, the third side BD may be found by the first Proposition.

4. Having the three sides of a right Line Triangle, to find the three Angles.

Let one of the three sides given be the Base, but rather the greater side, that the Perpendicular may fall within the Triangle; then gather the sum, and the difference of the other two sides, and the proportion will hold.

• As the Base of the triangle, is to the sum of the sides:
• So the difference of the sides to a fourth, which being taken forth of the Base, the Perpendicular shall fall on the middle of the remainder.

As in the former Triangle ADB, where the Base AB is 335, the sum of the sides AD and DB 371, and the difference of them 171. If I extend the Compasses in the Line of Numbers from 335 unto 371, I hsal find the same entent to reach from 171 unto 189.4. This fourth Number I take out of the Base 335.0. and the remainder is 145.6, the half whereof is 72.8, and doth shew the distance from A unto H, where the Perpendicular shall fall, from the Angle D, upon the Base AB, dividing the former Triangle ADB into two right Angle Triangles, DHA and DHB, in which the Angles may be found by the second Proposition.

And this may suffice for the right Line Traingles, but for the more easie protraction of these Triangles, I will set down one more Proposition more concerning Chods.

5. Having the Semidiameter of a Circle, to find the Chord of the Ark.

• As the Sine of the Semiradius of 32 gr. to the Sine of half the Ark proposed:
• So ist the Semidiameter of the Circle given, to the Chord of the same Ark.

As if in the protracting te former Triangle ADB, it were required to find the length of a Chord of 43 gr. 20 m agreeing to the Semidiameter AE, which is known to be three Inches. The half of 43 gr. 20 m. is 21 gr. 20 m. wherefore I extend the Compasses from the Sine of 30 gr. to the Sine of 21 gr. 20m. and I find the same extent to reach in the Line of Numbers from 3.000 parts to 2.215. which shews, that the Semidiameter being three Inches, the Chord of 43 gr. 20 m. will be 2 Inches and 215 parts of 100.

In like manner the Cord of 58 gr. agreeing to the same Semidiameter, would be found to be 2 inches and 909 parts. For half of 58 being 29; if I extend the Compasses in the Line of Sines from 30 gr. to 29 gr. the same extent will reach in the Line of Numbers from 3.000 unto 2.909.

Or in Cross work, if I extend the Compasses from the Sine of 30 gr. unto 3.000 in the Line of Numbers, I shall find the same extent to reach from 21 gr. 40 m. to 2.215 parts, and from 29 gr. to 2.909 parts, and from 7 gr. 20 m. to 795 parts; for the Cord of 14 gr. 40 m. for the third Angle ABD.