The Second Book of the Cross-Staff
Chap. V
Containing such Astronomical Propositions as are of ordinary use in the practice of Navigation.
1. To find the Altitude of the Sun by the shadows of a Gnomon set Perpendicular to the Horizon.
- As the parts of the shadow, are to the parts of the Gnomon:
- So the Tangent of 45 gr. to the Tangent of the Altitude.
Extend the Compasses in the Line of Numbers, from the parts of the shadow to the parts of the Gnomon; the same extent will give the distance from the Tangent of 45 gr. to the Tangent of the Suns Altitude.
So the Gnomon being 36, and the shadow 27, the Altitude will be found to be 36 gr. 52 m. Or the Gnomon being 27, and the shadow 36 the Altitude will be found to be 53 gr. 8 m. Or the shadow being 20, and the Gnomon 9, the Altitude will be found to be 24 gr. 14 m. as in the eighth Proposition of the use of the Tangent-line.
If the Gnomon be 22. and the shadow 135, the Altitude is 9 gr. 15 m. as I shewed before.
2. Having the distance of the Sun, from the next Equinoctial point, to find his declination.
- As the Radius is in proportion, to the Sine of the Suns greatest declination:
- So the Sine of the Suns distance from the next Equinoctial point, to the Sine of the Declination required.
Extend the Compasses in the Line of Sines, from 90 gr. to 23 gr. 30 m. the same extent will give the distance from the Suns place unto his Decination.
So the Sun being either 29 gr. of Taurus, or 1 gr. of Aquarius, or 1 gr. of Leo, or 29 gr. of Scorpio, that is 59 gr. distant from the next Equinoctial Point, the Declination will be found about 20 gr.
If the Sun be so near the Equinoctial Point, that his Declination fall to be under 1 gr. it may be found by the Line of Numbers. As if the Sun were in 2 gr. 5 m. of Aries, that is 125 m. from the Euqinoctial Point, the former extent of the Compasses from the Sine of 90 gr. to the Sine of 23 gr. 30 m. will reach in the Line of Numbers from 125 unto 50, which shews the Declination to be about 50 m.
3. Having the Latitude of the place, and the Declination of the Sun, to find the time of the Suns rising and setting.
- As the Co-tangent of the Latitude, to the Tangent of the Suns Declination:
- So is the Radius, to the Sine of the Ascensional difference between the hour of 6, and the time of the Suns rising or setting.
Extend the Compasses from the Tangent of the Complement of the Latitude, to the Tangent of the Declination: the same extent will reach from the Sine of 90 deg. to the Sine of the Ascensional difference.
Or extend the Compasses from the Co-tangent of the Latitude to the Sine of 90 gr. the same extent will reach from the Tangent of the Declination, to the Sine of the Ascensional difference.
So the Latitude being 51 gr. 30 m. Northward, and the Declination 20 gr. the difference of Ascension will be found to be 27 gr. 14 m. which resolved into hours and minutes, doth give 1 hour and almost 49 m. for the difference between Suns rising or setting, and the hour of 6, according to the time of the year.
4. Having the latitude of the place, and the distance of the Sun, from the next Equinoctial point, to find his Amplitude.
- As the Co-sine of the Latitude, to the Sine of the Suns greatest Declination:
- So the Sine of the place of the Sun, to the Sine of the Amplitude.
So the Latitude being 51 deg. 30 m. and the place of the Sun in 1 deg. of Aquarius, that is 59 deg. distant from the next Equinoctial point, the Amplitude will be found about 33 deg. 30 m. For extend the Compasses in the Line of Sines, from 38 deg. 30 m. the Sine of the Complement of the latitude unto 23 deg. 30 m. the Sine of the Suns greatest Declination; the same extent will reach from 59 deg. unto 33 deg. 20 m. Or extend them from 38 deg. 30 m. unto 59 deg. the same extent will reach from 23 gr. 30 m. unto 33 gr. 20 m. as before.
5. Having the Latitude of the place, and the Declination of the Sun, to find his Amplitude.
- As the Co-sine of the Latitude, is to the Radius:
- So is the Sine of the Declination, to the Sine of the Amplitude.
Extend the Compasses from the Co-sine of the latitude to the sine of 90 gr. the same extent will reach from the Sine of the Suns Declination to the Sine of the Amplitude.
Or extend them from the Tangent of the latitude to the Sine of the Declination, the same extent will reach from the Sine of 90 gr. To the Sine of the Amplitude.
So the latitude being 51 gr. 30 . and the Declination 20 gr. The Amplitude will be found to be 33 gr. 20 m.
6. Having the latitude of the place, and the Declination of the Sun, to find the time when the Sun cometh to be due East or West.
- As the Tangent of the Latitude, is to the Tangent of the Declination:
- So the Radius to the Co-sine of the hour from the Meridian.
Extend the Compasses from the Tangent of the Latitude the Tangent of the Declination, the same extend will reach from the Line of 90 gr. To the Sine of the Complement of the hour.
Or extend them from the Tangent of the latitude to the Sine of 90 gr., the same extent will reach from the Tangent of the Declination to the Sine of the Compliment of the hour.
So the Latitude being 51 gr. 30 m. and the Declination 20 gr. The Sun will be 73 gr. 10 m. that is 4 hours, and 53 m. from the Meridian, when he cometh to be in the East or West.
7. Having the latitude of the place, and the Declination of the Sun, to find what Altidude the Sun shall have, when he cometh to be due east or West.
- As the Sine oft he Latitude, ist o the Sine oft he Declination:
- So the Radius, to the Sine of the Altitude.
Extend the Compasses in the Line of Sines from the Latitude to the Sine of the Declination, the same extent will reach from the Sine of 90 gr. To the Sine of the Altitude.
Or extend them from the Sine of the Latitude to the Sine of 90 gr. The same extent will reach from the Sine of the Declination to the Sine of the Altitude.
So the Latitude being 51 gr. 30 m. and the Declination 20 gr. The Altitude will be found about 25 gr. 55 m.
8. Having the Latitude of the place, and the Declination of the Sun, to find what Altitude the Sun shall have at the hour of six.
- As the Radius is in proportion, to the Sine of the Suns Declination:
- So the Sine of the Latitude, to the Sine of the Altitude.
Extend the Compasses in the Line of Sines, from 90 gr. To the Declination; the same extent will reache from the Latitude to the Altitude.
Or extent them from 90 gr. To the Latitude, the same extend will reach from the Declination to the Altitude.
So the Latutude being 51 gr. 30 m. and the Declination of the Sun 20 gr. The Altitude of the Sun will be found to be about 15 gr. 30 m.
9. Having the Latitude of the place, and the Declination of the Sun, to find what Azimuth the Sun shall have at the hour of six.
- As the Co-tangent of the Suns Declination,
- So the Tangent of the Azimuth from the North part of the Meridian.
So the Latitude being 51 gr. 30 m. and the Declination 20 gr. The Azimuth will be found to be 77 gr. 14 m. For extend the Compasses in the Line of Sines, from 38 gr. 30 m. to 90 gr. The Same extent will reach from the Tangent of 70 gr. To the Tangent of 77 gr. 14 m.
10. Having the Latitude of the Place, and the Declination of the Sun, and the Altitude of the Sun, to find the Azimuth.
First, consider the Declination of the Sun, whether it be toward the North or the South, so have you his distance from your Pole: then add this distance, the Compliment of his Altitude, and the Complement of your Latitude, all three together, and from half the sum subtract the distance from the Pole, and note the difference.
- As the Radius is in proportion, to the Co-sine of the Altitude:
So the Co-sine of the Latitude, to a fourth Sine. - As this fourth Sine, is to the Sine of the half sum:
So is the Sine of the difference, to a seventh Sine.
Then find a mean proportional between this seventh Sine and the Radius, this mean shall be the Sine of the Compliment of half the Azimuth from the North part of the Meridian.
Suppose the Declination of the Sun being known by the time of the year to be 20 gr. Southward, the Altitude above the Horizon found by observation 12 gr. And the Latitude Northward 51 gr. 30 m. it were required to find the Azimuth.
The declination ist Southward, and therefore the distance from the Pole 110 gr. Then turning the Altitude and Latitude into their Complements, I add them all three together, and from half the sum subtract the distance from the Pole, noting the difference after this manner:
| Declin | South | 20 gr. | 0 m. | The Distance | 110 gr. | 0 m. |
| Altitude | 12 | 0 | The Compliment | 78 | 0 | |
| Latitude | N | 51 | 30 | The Compliment | 38 | 30 |
| The sum of all three | 226 | 30 | ||||
| The half sum | 113 | 15 | ||||
| The difference | 3 | 13 |
This done, I come to the Staff, and extend the Compasses from the Sine of 90 gr. To the Sine of 78 gr. And find the same extent to reach from the Sine of 38 gr. 30 m. unto 37 gr. 30 m. Or if I extend them from from 90 gr. To 38 gr. 30 m. the same extent doth reach from 78 gr. Unto 37 gr. 30 m. which is the fourth Sine required.
Then I extend the Compasses again from this fourth Sine of 37 gr. 30 m. unto the Sine of the half sum 113 gr. 15 m. that is to the Sine of 66 gr. 45 m (for after 90 gr. The Sine of 80 gr. Doth stand for a Sine of 100 gr. and the Sine of 70 gr. for a Sine of 100 gr. and so the rest for those which are their Compliments to 180 gr.) and this second extent doth reach from the Sine of the difference 3 gr. 15 m. to the Sine of 4 gr. 54 m. Or if I extend them from the fourth Sine of 37 gr. 30 m. to the Sine of the difference 3 gr. 15 m. the same extent will reach from the Sine of the half sum 113 gr. 15 m. unto 4 gr. 54 m which is the seventh Sine required.
Lastly, I divide the space between the seventh Sine of 4 gr. 54 m. and the Sine of 90 gr. into two equal parts, and I find the mean proportional side to fall on 17 gr. whose Complement is 73 gr. the double of 73 gr. is 146 gr. and such is the Azimuth required.
Or having found the seventh Sine to be 4 gr. 54 m. I might look over against it, in the Line of Versed Sines, and there I should find 146 gr. for the Azimuth from the North part of the Meridian; and the Compliment of 146 gr. to a Semicircle being 34 gr. will give the Azimuth from the South part of the Meridian.
But if it were required to find the Azimuth in the same Latitude of 51 gr. 30 m Northward, with the same Altitude of 12 gr. and like Declination of 20 gr. to the Northward, it would be found to be only 72 gr. 52 m. though the manner of work be the same as before.
| Declin | North. | 20 gr. | 0 m. | The Distance | 70 gr. | 0 m. |
| Altitude | 12 | 0 | The Compliment | 78 | 0 | |
| Latitude | North. | 51 | 30 | The Compliment | 28 | 30 |
| The sum of all three | 186 | 30 | ||||
| The half sum | 93 | 15 | ||||
| The difference | 23 | 13 |
Here as the Radius is to the Sine of 78 gr. so the Sine of 38 gr. 30 m. to the Sine of 37 gr. 30 m. which is the fourth Sine, and the same as before.
Then as this fourth Sine of 37 gr. 15 m. is to the Sine of 93 gr. 15 m. so the Sine of 23 gr. 15 m. to the Sine of 40 gr. 20 m. which is the seventh Sine.
The half way between the seventh Sine and the Sine of 90 gr. doth fall at 53 gr. 34 m whose Complement is 36 gr. 26 m. and the double of that is 72 gr. 52 m. the Azimuth required.
Or I may find the same Azimuth in the Line of Versed Sines, over against the seventh Sine of 40 gr. 20 m.
11. Having the latitude of the place, the Declination of the Sun, and the Altitude of the Sun, to find the hour of the day.
Add the Complement of the Suns Altitude, and the distance of the Sun from the Pole, and the Complement of your Latitude, all three together, and from half the sum subtract the Complement of the Altitude, and note the difference.
- As the Radius is in proportion to the Sine of the Suns distance from the Pole:
So the Sine of the Complement of the Latitude, to a fourth Sine. - As this fourth Sine, is to the Sine of the half sum:
So the Sine of the difference to a seventh Sine.
The mean proportional between this seventh Sine and the Sine of 90 gr. will be the Sine of the Complement of half the hour from the Meridian.
Thus in our Latitude of 51 gr. 30 m. the Declination of the Sun being 20 gr. Northward, and the Altitude 12 gr. I might find the Sun to be 95 gr. 52 m. from the Meridian.
| Altitude | 12 gr. | 0 m. | The Complimen is | 78 gr. | 0 m. |
| Decl. North. | 20 | 0 | The diff. from the Pole | 70 | 0 |
| Latitude | 51 | 30 | The Compliment is | 38 | 30 |
| The sum of all three | 286 | 30 | |||
| The half sum | 93 | 15 | |||
| The difference | 15 | 15 |
- Here as the Radius, is to the Sine of 70 gr
- So the Sine of 38 gr. 30 m. to the Sine of 35 gr. 48 m.
- As this Sine of 15 gr. 48 m. is to the Sine of 93 gr. 15 m.
- So the Sine of 15 gr. 15 m. to the Sine of 26 gr. 40 m.
The half way between this seventh Sine of 26 gr. 40 m. and the Sine of 90 gr. doth fall at 42 gr. 4 m. whose Complement is 47 gr. 56 m. and the double of that, 95 gr. 52 m. which converted into hours, doth give 6 hours and almost 24 m. from the Meridian.
Or I might find these 95 gr. 52 m. in the Line of Versed Sines, over against the seventh Sine of 26 gr. 40 m.
12. Having the Azimuth, the Suns Altitude, and the Declination, to find the hour of the day.
- As the Co-sine of the Declination, ist to the Sine of the Azimuth:
- So the Co-sine of the Altitude, to the Sine of the hour.
Thus the Declination being 20 gr. Southward, the Altitude 12 gr. and the Azimuth found by the tenth Proposition 146 gr. I might find the time to be 35 gr. 36 m that is 2 hours 22 m. from the Meridian.
13. Having the hour of the day, the Suns Altitude, and the Declination, to find the Azimuth.
- As the Co-sine of the Altitude, into the Sine of the hours:
- So the Co-sine of the Declination, to the Sine of the Azimuth.
So the Altitute of the Sun being 12 gr. and the Declination 20 gr. Southward, and the Angle of the hour 35 gr. 36 m. I should find the Azimuth to be 34 gr. And so it is if it be reckoned from the South; but 146 gr. if it be taken from the North part of the Meridian.
14. Having the distance of the Sun from the next Equinoctial point, to find his right Ascension.
- As the Radius, to the Co-sine of the greatest Declination:
- So the Tangent of the distance, to the Tangent of the right Ascension.
So the Sun being in the first degree of Aquarius, that is 59 gr distant from the next Equinoctial point, and the greatest Declination 23 gr. 30 m. the right Ascension will be found to be 56 gr. 50 m short of the beginning of Aries, and therefore 303 gr. 14 m.
15. Having the Declination of the Sun, to find his right Ascension.
- As the Tangent of the greatest Declination, is to the Tangent of the declination given:
- So the Radius to the Sine of the right Ascension.
So the greatest Declination being 23 gr. 30 m. and the Declination of the Sun given 20 gr. the right Ascension will be found about 56 gr. 50 m.
16. Having the Longitude and latitude of a Star, to find the right Ascension of that Star.
17. To find the Declination of that Star.
The stars have little or no alteration in their Latitude, in their Longitude they move forward, about 1 gr 25 m. in hundred years. These being known,
- As the Radius, to the Sine of the Stars Longitude from the next Equinoctial point:
- So the Co-tangent of the stars Latitude, to the Tangent of a fourth Ark.
Compare this fourth Ark, with the Ark of distance between the Poles of the world and of the Ecliptick. If the Longitude and the latitude of the Star be both alike, as when the Longitude falleth to be among the Northern Signs, Aries, Taurus, Gemini, Cancer, Leo, Virgo, and the Latitude is North from the Ecliptick: or the Longitude among the Southern signs, Libra, Scorpio, Sagitarius, Capricorn, Aquarius, Pisces, and the Latitude Southward, then shall the difference between this fourth Ark and the distance of Poles, be your fifth Ark.
But if the Longitude and latitude shall be unlike, as the Longitude in a Northern sign, and the Latitude South, or the Longitude in a southern Sign, and the Latitude North, then add this fourth Ark to the distance of both Poles, the sum of both shall be your fifth Ark. And,
- As the Sine of the fourth Ark, to the Sine of the fifth Ark:
- So the Tangent of the stars Longitude, to the Tangent of the stars right Ascension, from the next Equinoctial point.
- As the Co-sine of the fourth Ark, to the Co-sine of the fifth Ark:
- So the Sine of the stars Latitude, to the Sine of the stars Declination.
Then for proof of the work, if there be no former error, the proposition will hold.
- As the Co-sine of the Latitude, to the Co-sine of the right Ascension:
- So the co-Sine of the Declination, to the Co-sine of the Longitude.
For example, Take the upper of the two former stars in the square of the little bear, which sea-men call the Former Guard. This in the year 1655, was in 7 deg. 53 m. of Leo, and so his Longitude from the beginning of Libra 52 deg. 7 m. But his latitude is still the same 72 gr. 51 m Northwards. Wherefore,
- As the Sine of 90 gr. is to the Sine of 52 gr. 22 m
- So the Co-tangent of 72 gr. 51 m. to the Tangent of 13 gr. 44 m.
Which is the fourth Ark. Then because the Longitude and Latitude are both Northward, the difference between this fourth Ark and 23 gr. 31 m. the distance of both Poles will give you 9 gr. 47 m. for the fifth Ark. And,
- As the Sine of 13 gr. 44 m. to the Sine of 9 gr. 47 m.
- So the Tangent of 52 gr. 22 m. to the tangent of 42 gr. 56 m.
Which is the right Ascension of this star, from the beginning of Libra, but 222 gr 56 m. from the beginning of Aries.
- As the Co-sine of 13 gr. 44 m. to the Co-sine of 9 gr, 47 m.
- So the Sine of 72 gr. 51 m to the Sine of 75 gr. 46 m.
Which is the Declination of this star from the Equator.
- As the Co-sine of 72 gr. 51 m to the Co-sine of 42 gr 56 m
- So the Co-sine of 75 gr. 46 m to the Co-sine of 52 gr. 7 m.
Which agreeing so well with the Longitude of the star proposed is a good proof, that the Ascension and Declination were truly found.
These are such Astronomical Propositions, as I take to be useful for Sea-man. For the first and second will help them to find their latitude, the third to find the Suns rising and setting, the 4, 5, 6, 7, 8, 9, 10, 13 Prop. To find the variation of their Compass, the 11 and 12 Pro. To find the hour of the day; and the rest toward the finding of the hour of the night. For having the latitude of the place, with the Declination and Altitude of any star, they may find the hour of the star from the Meridian, as in the 11 Prop. Then comparing the right Ascension of the star, with the right Ascension of the Sun, they may have to the hour of the night.
All these Propositions, and such others, may be wrought also by the Table of Sines and Tangents. For where four Numbers do hold in proportion; as the first to the second, so the third to the forth; there if we multiply the second into the third, and divide the Product by the first, the Quotient will give the fourth required. As in the example of the 15 Prop. Where the Declination being given, it was required to find the right Ascension. The Tangent of 20 gr. the Declination given is 3639702, which being multiplied by the Radius, the Product is 36397020000000, and this divided by 4348124, the Tangent of 23 gr. 30 m the Quotient is 8370741, the Sine of 56 gr. 50 m. for the right Ascension required.
Or if any will use my Tables of Artificial Sines and Tangents, they may add the second and third together, and from the sum subtract the first, the remainder will give the fourth required. And so my Tangent of 20 gr. is 9561,0658, which being added to the Radius, makes 19501,0658, from this if they subtract 9638,3019, the Tangent of 23 gr. 30 m. they shall find the remainder to be 9922,7639, which in my Canon is the Sine of 56 gr. 49 m. 56 seconds; and such ist the right Ascension required, if it be reckoned from the next Equinoctial point.
The like reason holdeth for all other Astronomical Propositions, as I will farher shew by those two examples which I gave before, for the finding of the Azimuth in the 10 Prop. Because they are thought to be harder than the rest, and require three operations.
In the first Example.
| Declin | South | 20 gr. | 0 m. | The Distance | 110 gr. | 0 m. |
| Altitude | 12 | 0 | The Compliment | 78 | 0 | |
| Latitude | N | 51 | 30 | The Compliment | 38 | 30 |
| The sum of all three | 226 | 30 | ||||
| The half sum | 113 | 15 | ||||
| The difference | 3 | 13 |
The first operation will be to find the fourth Sine; and that is done by adding the Sine of the Compliment of the Altitude to the Sine of the Compliment of the Latitude, and subtracting the Radius: so adding 9990,4044 the Sine of 78 gr. Unto 9794,1495 the Sine of 38 gr. 30 m. the sum will be 19785,5539. And the Radius being subtracted, the remainder 9784,5539 is the fourth Sine, and belongeth to 37 gr. 30 m.
The second operation will be to find the seventh Sine, and that is done by adding the sine of the half sum to the sine of the difference, and subtracting the fourth sine. So the half sum being 113 gr. 15. I take his Complement to a Semi-circle, and so find his line to be 9663,2168, to which I add 8753,5278, the sine of the difference 3 gr. 15 m. and the sum is 18716,7446. From this I take the fourth sine 9784,5539, and the remainder will be 8932,1907, which is the seventh sine, and belongeth to 4 gr. 54 m.
The third operation will be to find the mean proportional sine between the seventh sine and the Radius. This in common Arithmetick is done by multiplying the teo extreams, and taking the square root of the Product. As in finding a mean proportional between 4 and 9, we multiply 4 into 9, and the Product is 36, whose square root is 6, the mean proportional between 4 and 9. But ehre it is done by adding the sine and the Radius, and taking the half of them. So the sum of the last seventh sine and the Radius is 18932,1907, and the half of that 9466,0953, which is the mean proportional sine required, and belongeth to 17 gr. Whose Complement is 73 gr. And the double of that 146 gr. The same Azimuth as before.
In the second Example.
| Declin | North. | 20 gr. | 0 m. | The Distance | 70 gr. | 0 m. |
| Altitude | 12 | 0 | The Compliment | 78 | 0 | |
| Latitude | North. | 51 | 30 | The Compliment | 28 | 30 |
| The sum of all three | 186 | 30 | ||||
| The half sum | 93 | 15 | ||||
| The difference | 23 | 13 |
The first operation will be to find the fourth sine, and that is here 9784,5539, as in the former Example.
The second operation will be to find the seventh sine; and so here the sine of the half sum 93 gr. 15 m. being the same with the sine of 86 gr. 45 m. his Complement to 180 gr. I find it to be 9999,3009, to which I add 9596,3153, the sine of the difference 23 gr. 15 m. and the sum is 19595,6162. From this I take the fourth sine 9784,5539, and the remainder will be 9811,0623 for the seventh sine, and belongeth to 40 gr. 20 m.
The third operation will be to find the mean proportional Sine between the seventh Sine and the Radius. And so here the Radius being added to the seventh Sine, the sum will be 19811,0623, and the half of that 9905,5311, doth give the mean proportional Sine belonging to about 53 gr. 34 m. whose Complement is 36 gr. 26 m. and the double of that 72 gr. 52 m. the same Azimuth as before.
I have set down these three Examples thus particularly, that I might shew the adreement between the Staffe and the Canon. But otherwise I might deliver both the Precept and the Work, for the two last, more compendiously. For generally in all Spherical Triangles, where three sides are known, and an Angle required, make that side which is opposite the Angle required, to be the Base; and gather the sum, the half sum, and the difference as before.
- As the Rectangle contained under the Sines of the sides, is to the Square of the whole Sine:
- So the Rectangle contained under the Sines of the half sum und the difference, to the square of the Co-sine of the half Angel.
Then for the work, we may for the most part leave out the two last figures; and if they be about 50, put an unite to the sixth place, after this manner.
| 70 gr. | 0 m. |
 |
|||
| 78 | 0 | 9990 | 40 | ||
| 38 | 30 | 9794 | 15 | ||
| 186 | 30 | 19784 | 55 | ||
| 93 | 15 | 9999 | 30 | ||
| 23 | 15 | 9596 | 32 | ||
| 20000 | 00 | ||||
| 38595 | 62 | ||||
| 19811 | 17 | ||||
| 36 | 26 | 9905 | 53 | 53 gr. | 34 m. |
| 72 | 52 | 107 | 8 | ||
Or for such Numbers as are to be subtracted, I may take them out of the Radius, and write down the residue, and then add them together with the rest. As in the second Example, the Sines of 78 gr. And of 38 gr. 30 m. being the Numbers to be subtracted; if I take 9990,4044 the Sine of 78 gr. Out of the Radius 10000,0000, the residue is 9.5956: and so the residue of 9794,1495 is 205.8505. Wherefore instead of subtracting those Sines, I may add these residues after this manner:
| 70 gr. | 0 m. | ||||
| 78 | 0 | 9 | 59 | ||
| 38 | 30 | 205 | 85 | ||
| 186 | 30 | ||||
| 93 | 15 | 9999 | 30 | ||
| 23 | 15 | 9596 | 32 | ||
| 19811 | 66 | ||||
| 38595 | 62 | ||||
| 36 | 26 | 9905 | 53 | 53 gr. | 34 m. |
| 72 | 52 | 107 | 8 | ||
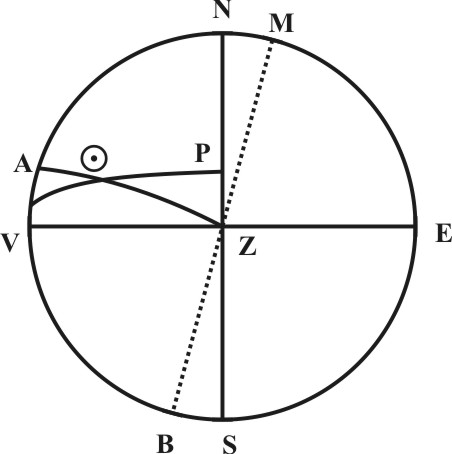
Having these means to find the Suns Azimuth, we may compare it with the Magnetical Azimuth, and so find the variation of the Needle.
Let for the Circle AMB, drawn by the Center Z, be a Plane, parallel to the Horizon; A the Point whereon the Sun bears from us, M the North point of the Magnetical Needle, and the Angle AZM, the Magnetical Azimuth. If we find the Suns Azimuth as before, to be 72 gr. 52 m. from the North to the Westward, we may allow so many gr. From A unto N, and so have the true North point of the Meridian, and consequently, the East, South, and West Points of the Horizon, and the distance between N and M shall be the variation of the Needle. So that if the Magnetical Azimuth AZM shall be 84 gr. 7 m. and the Suns Azimuth AZN 72 gr. 52 m. then must NZM the difference between the two Meridians, give the variation to be 11 gr. 15 m. as Mr. Borough heretofore found by his observations at Limehouse in the year 1589. But if the Magnetical Azimuth ZM shall be 79 gr. 7 m. and the Suns Azimuth AZN 72 gr. 52 m. then shall the variation NZM be only 6 gr. 15 m as I have sometimes found it of late. Hereupon I enquired after the place where Mr. Borough observed, and went to Limehouse with some of my friends, and took with us a Quadrant of three foot Semidiameter, and two Needles, the one above 6 inches, and the other 10 inches long, where I made the Semidiameter of my Horizontal Plane AZ 12 inches: and towards night the 13 of June 1622, I made observation in several parts of the ground, and found as followeth:
| Alt. |
AZM | AZN | Variat | ||||
|---|---|---|---|---|---|---|---|
| Gr. | M. | Gr. | M. | Gr. | M. | Gr. | M. |
| 19 | 0 | 82 | 2 | 75 | 52 | 6 | 10 |
| 18 | 5 | 80 | 50 | 74 | 44 | 6 | 6 |
| 17 | 34 | 80 | 0 | 74 | 6 | 5 | 54 |
| 17 | 0 | 79 | 15 | 73 | 20 | 5 | 55 |
| 16 | 18 | 78 | 12 | 72 | 32 | 5 | 40 |
| 16 | 0 | 77 | 50 | 72 | 10 | 5 | 40 |
| 10 | 20 | 71 | 2 | 64 | 49 | 6 | 13 |
| 9 | 25 | 70 | 12 | 64 | 25 | 5 | 47 |