The Third Book of the Cross-Staff
CHAP. VII.
To draw the Hour-lines in a Vertical Declining Plane.
All upright Planes whereon a man may draw a Vertical Line, are in this respect said to be Vertical; if they shall also stand directly East and West, they are directly vertical; if directly North and South, they are properly called Meridian Planes, and are described before: if they behold none of these four principal Parts of the world, but shall stand between the prime Vertical and the Meridian, they are then called by the general name of Declining Verticals.
These have two faces, one to the South, the other to the Northward, which may be distinguished in these Northern parts of the World after this manner. If the Sun coming to the Meridian shall shine upon the Plane, it is the South Face; if not, it is the North face of the Plane. Again, if the Sun shall shine upon the Plane at High-noon, and yet longer in the Forenoon than in the Afternoon, it is the South-east Face; if longer in the Afternoon than in the Forenoon, it is the South-west Face of the Plane. But how much the Declination cometh to, is best found as before.
When the Declination is found, there be four things to be considered, before we can come to the drawing of the Hour-lines.
- The Meridian of the Plane, and his Inclination to the Meridian of the Place.
- The height of the Pole above the Plane.
- The Distance of the Substylar from the Meridian Line.
- The Distance of each Hour-line from the Substylar.
And these four may all be represented in the Fundamental Diagram, as in this Example.
Suppose that in our Latitude of 51 gr. 30 m. Northward the Declination of an upright Plane should be found to be 24 gr. 20 m.
In the Triangle PRZ we know the Angle at R to be a Right Angle, and the Angle at Z, for it is the Complement of the declination; and the Base PZ, for it is the Complement of the Latitude. And these three being known, we may find the other Angle RPZ, which is the Angle of the Inclination between both Meridians.
- As the Sine of the Latitude is to the Sine of 90 gr.
- So is the Tangent of the Declination to the Tangent of the Inclination of Meridians.
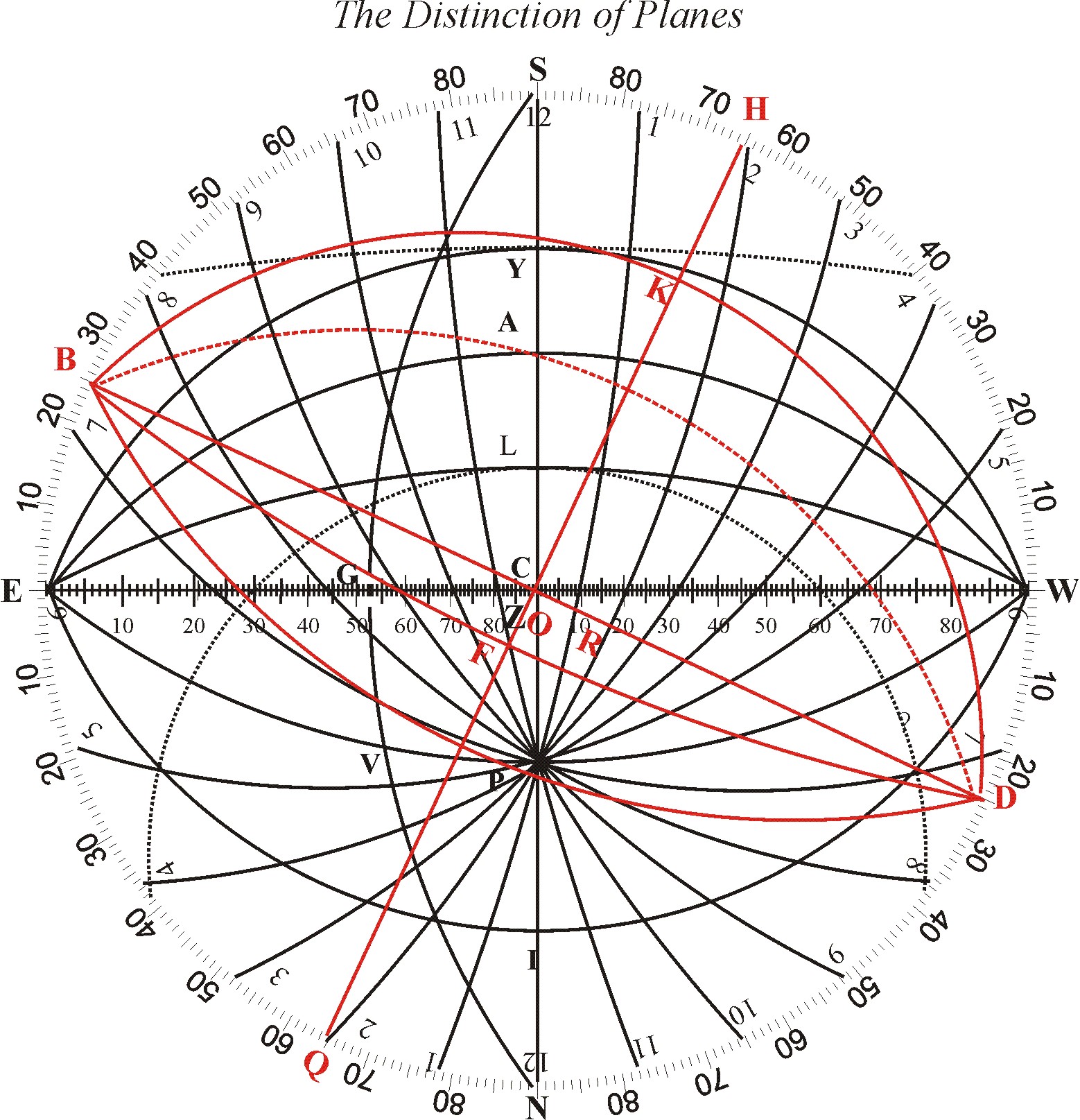
Thus in our former Example I extend the Compasses from the Sine of the Latitude 51 gr. 30 m. unto the Sine of 90 gr. the same extent will reach in the Line of Tangents from 24 gr. 20 m. the Declination given, to about 30 gr. and such is ZPR, the Angle of Inclination between the Meridian of the Place and the Meridian of the Plane: and therefore the Meridian of the Plane will here fall upon the Circle of the second Hour from the Meridian of the Place (as it may also appear by opening the Compasses to the nearest extent between the Pole and the Plane) and there I place the Letter R to make this Rectangle PRZ.
To find the Height of the Pole above the Plane.
The height of the Pole is to be measured in the Meridian of the Plane; it is here represented by the Ark PR, and may be found by that which we have known in the former Triangle PRZ.
- As the Sine of 90 gr. to the Co-sine of the Latitude:
- So the Co-sine of the Declination, to the Sine of the Height of the Pole above the Plane.
Extend the Compasses from the Sine of 90 gr. unto the Sine of 38 gr. 30 m. the Complement of the Latitude, and the same extent will reach from the Sine of 65 gr. 40 m. the Complement of the Declination, unto the Sine of 34 gr. 33 m.
Or if you please to make use of the Angle of Inclination of the two Meridians, the proportion will hold,
- As the Sine of 90 gr to the Co-sine of the Inclination of Meridians:
- So the Tangent of the latitude, to the Tangent of the height of the Pole above the Plane.
And then you may extend the Compasses from the Sine of 90 gr. unto the Sine of 60 gr. the Complement of the Inclination of the Meridians, and the same extent will reach from the tangent of 38 gr. 30 m. the Complement of the Latitude, unto the Tangent of 34 gr. 33 m. and such is the Ark PR the Height of the Pole above the Plane.
To find the Distance of the Substylar from the Meridian.
This is here represented by the Ark ZR, and may be found by that which we have known in the former Triangle PRZ.
- As the Sine of 90 gr. to the Sine of the declination:
- So the Co-tangent of the Latitude, to the Tangent of the Substylar from the Meridian.
Extend the Compasses from the Sine of 90 gr. unto the Sine of 24 gr. 20 m. the Declination given, and the same extent will reach from the Tangent of 38 gr. 30 m. the Complement of the Latitude, unto the tangent of 18 gr. 8 m. and such is the Ark ZR, the Distance of the Substylar from the Meridian.
To find the Distance of each Hour-line from the Substylar.
The Distance of the Hour-lines from the Substylar are here represented by these Arks of the declining Vertical belonging to the Plane, which are intercepted between the proper Meridian of the Plane and the Hour-circles.
To this purpose we have divers Triangles made by the Declining Plane, together with his proper Meridian and the Hour-circles. In these we have known, first the Right Angle at the Intersection of the proper Meridian with the Plane; then the Side which is the Height of the Pole above the Plane; and thirdly, the Angles at the Pole. For knowing the Angle of Inclination between the Meridian of the Plane and the Meridian of the Place, which is always the Hour of 12, we may find the Angle between the Meridian of the Plane and the Hour of 1, by allowing in 15 gr. for the Angle between the Meridian of the Plane and the Hour of 2, by allowing in 30 gr. and so for the rest: which being known, and set down in a Table, we may find the Arks of the Plane from the Substylar to the Hour-circles, in this manner,
- As the Sine of 90 gr. to the Sine of the Height of the Pole above the Plane:
- So the Tangent of the Hour from the proper Meridian, to the Tangent of the Hour-line from the Substylar.
Thus in our Latitude of 51 gr. 30 m. if the Declination of an upright Plane shall be found to be 24 gr. 20 m. from the prime Vertical, the one Face open to the South-west, the other to the North-east, I may number these 24 gr. 20 m. in the Horizon of the Fundamental Diagram from E unto B, according to the situation of the Plane, and there draw the Vertical BZD, which shall represent the Plane proposed.
The two Poles of this Plane will fall in the Horizon at H and Q and therefore the proper Meridian drawn through the Poles of the Plane and the Pole of the World must be the Circle HPQ, which here crosseth the Plane at Right Angles in the Point of R, and inclineth to PZS the Meridian of the Place, according to the Angle RPZ.
The quantity of this Inclination may be readily found by the Hour-circle where the proper Meridian falleth. As here it falleth on the second Hour-circle, and so the Inclination is 30 gr.
The height of the Pole above the Plane, which giveth the height of the Style above the Substylar, is here represented by the Ark PR. For as in the Horizontal, so in this and all other Planes, the Line CP the Axis of the World is always the Axis of the Style, and the nearest Line that can be drawn upon the Plane to the Axis of the World is the fittest for the Substylar, and this is the Line CR: so the Angle PCR is the Angle between the Axis and the Plane, commonly called the height of the Style, and the measure of this Angle is the Ark PR. This Ark is always less than the Complement of the latitude, and may be estimated by taking the distance PR with the Compasses, and measuring it in the Meridian from P toward Z. So in this Example it will appear to be about 34 gr ½.
The distance of the Substylar from the Meridian is here represented by the Ark ZR: For the Meridian Line upon the Plane is CZ, the Substylar Line is CR; so the Angle contained between them is ZCR, and the measure of this Angle is the Ark ZR, which taken with the Compasses, and measured in the Semidiameter CW, from C toward W, will be found about 18 gr.
The distances of each Hour-line from the Substylar are here represented by the Arks of the Plane between the Point R and the Intersections of the Hour-circles: For the Substylar Line is CR, and the Hour-circle of 1 crossing the Plane in the Point O, the Hour-line of 1 upon the Plane must be CO; so the Angle between the Substylar and the Hour-line of 1 is RCO, and the measure of this Angle is the Ark RO. In like manner, the Hour-line of 12 will be CZ, and the distance from the Substylar RZ: the Hour-line of 11 will be CX, and the distance from the Substylar RX: and so the rest. These distances RO, RZ, RX, &c. may also be taken with the Compasses, and measured as before.
Besides these four Representations, the Diagram will shew what Pole is elevated above the Plane, and what time the Sun shineth upon the Plane. If it be the North-west Face of this Plane, you may think P to be the North Pole, and the Hour-circles to be drawn on a Convex hemisphere; so CR the Substylar, and CP the Axis of the Style, will both point upward: and having drawn the Tropick of ♋, you shall find by the meeting of the Plane with the Tropick, and the Hour-circles, that the Sun at thze highest may shine upon the Plane from the time of the rising until it be past 9 in the morning, and from 7 in the evening unto the time of his setting. But if it be the South-west Face of the Plane, then you may either suppose the Substylar and the Axis to be continued down below the Center, like unto the Hours before and after 6 in an Horizontal Plane; or else you may turn the Diagram, and think P to be the South Pole, and the Hour-circles to be drawn in an Horizontal Concave so CR the Substylar, CP the Axis of the Style, will both point downward, and so also the Hour-circles from 8 in the morning until after 7 in the evening, as it doth appear by the meeting of the Plane with the Horizon, and the Hour-circles.
Thus with the drawing of one Line in the Diagram, to represent the Plane according to his declination, you may have the Hour-lines fitted to any Declining Vertical, with the Style and Substylar in their due place, which may suffice to free you from gross error; but for more exactness, we consider three Triangles.
To find the Inclination of Meridians.
The Meridian of the Place is a Circle passing through the Poles of the World, the Zenith and the Nadir. The proper Meridian of the Plane is a Circle passing through the Poles of the World and the Poles of the Plane. The Circle of the Plane and these two Meridians do make a Triangle, such as PRZ, wherein we know the Angle at R.
I consider the Angle of Inclination of the meridian RPZ, and there see how that PZ, the Meridian of the Place, which is the Hour of 12, being 30 gr. distant from PR the Meridian of the Plane, and that one Face of the Plane being open to the South-west, and the other to the North-east, this Meridian of the Plane falleth to be the same with the Hour of 2, (otherwise with the Hour of 10: therefore allowing 15 gr. for an Hour, the Hour of 1 RPO will be 16 gr. and RPX the Hour of 11 will be 45 gr. distant from PR the proper meridian of the Plane: And so I gather the Inclination of the rest of the Hour-circles towards the Meridian, according to their Angles at the Pole, as in the second Column of this Table.
| Latitude N. | 51 | 30 | |||
| Declinat. | 24 | 20 | |||
| Diff. Merid.. | 30 | 0 | |||
| Alt. Styl. | 34 | 33 | |||
| Dist. Subst. | 18 | 18 | |||
| Hours | Ang. Po. | Ar. Pla. | |||
| M. | E. | Gr. | M. | Gr. | M. |
| 4 | 8 | 90 | 00 | 90 | 00 |
| 5 | 7 | 75 | 00 | 64 | 42 |
| 6 | 6 | 50 | 00 | 44 | 30 |
| 7 | 5 | 45 | 00 | 29 | 33 |
| 8 | 4 | 30 | 00 | 18 | 8 |
| 9 | 3 | 15 | 00 | 8 | 38 |
| 10 | 2 | Merid. | Substyl. | ||
| 11 | 1 | 15 | 00 | 8 | 38 |
| 12 | 30 | 00 | 18 | 8 | |
| 1 | 11 | 45 | 00 | 29 | 33 |
| 2 | 10 | 50 | 00 | 44 | 30 |
| 3 | 9 | 75 | 00 | 64 | 42 |
| 4 | 8 | 90 | 00 | 90 | 00 |
Then taking my Compasses in my hand, I extend them from the Sine of 90 gr. unto the Sine of 34 gr. 33 m. the height of the Pole above the Plane, and find them to reach in the Line of Tangents from 15 gr. the Inclination of the Hour of 1, to 8 gr. 38 m. for the Ark of 1 from the Substylar, and from 30 gr. unto 18 gr. 8m for the Hour of 12, agreeable to the third Prop. and from 45 gr. unto 29 gr. 33 m. for the Hour of 11, and so the rest, which I also set down in the third Column of the Table.
These Arks being thus found, will serve for the drawing of the Hour-lines both on the South-west Face and the North-east Face of this Plane, and also on either Face of the like Plane that hath the same Declination, and the Poles in the South-east and North-west.
- By the Help of a Thred and Plummet I draw a Vertical Line, serving both for the Meridian of the Place, and the Hour of 12.
- In this Meridian Line I make choice of a Center at C, in the upper part of the Line if it be the South face, as here we suppose it, that the Style may have room to point downward: but in the lower part of the Line if it be the North Face of the Plane, for there the Style must point upward: and upon this Center I describe an occult Circle, representing the Declining Vertical belonging to the Plane.
- I find a Chord of 18 gr. 8 m. the distance of the Substylar from the Meridian of the Plane, and inscribe it into this Circle, from the Meridian unto A toward the right hand, because in this Example the meridian of the Plane falls among the Hours after Noon, (for otherwise it must have been inscribed toward the left hand) and there I draw the Line CA serving for the Substylar.
- According to the Table of Arks of the Plane from the Substylar, I find a Chord of 8 gr. 38 m. and inscribe it into this Circle, from the Substylar toward the Meridian for the Hour of 1. In like manner a Chord of 29 gr. 32 m. for the Hour of 11, and a Chord of 44 gr. 30 m. for the Hour of 10; and so the rest of the Hours, their Halfs, and Quarters.
- I draw Right Lines through the center and the Terms of these Chords, and these Lines so drawn are the Hour-lines required.
Lastly, I set up the Style over the Substylar, so as it may cut the Plane in the center, and there make an Angle with the Substylar of 34 gr. 33 m. according to the height of the Pole above the Plane; so it shall represent the Axis of the World, and be truly placed for casting the Shadow upon the Hour-lines in this Declining Plane.
A second Example.
Suppose another upright Plane in the same Latitude to decline from the Vertical 65 gr. 44 m. with one Face open to the South-east, the other to the North-west. These 65 gr. 40 m. would be numbered from E unto Q, and from W unto H, and the Plane represented by QZH: For so the one Pole will fall at B in the South-east, and the other at D in the North-west, according to the supposition. The proper Meridian of this Plane may be supplied by the Circle BPD, crossing the Plane in the Point T, between the Hours of 7 and 8, and there is the place of the Substylar. The South-east Face will contain all Hours from Sun-rising unto 2 after Noon; and the North-west Face, all Hours from 1 after Noon unto Sun-setting. Then work as before,
- The Angle ZPT, the Inclination of the two Meridians, will be found to be about 70 degrees 30 minutes.
- The Ark PT, the measure of the Angle PCT, the height of the Pole above the Plane, and so the height of the Style above the Substylar, will be 14 gr. 51 m.
- The Ark ZT, the measure of the Angle ZCT, shewing the distance on the Substylar from the Meridian, will be 35 gr. 56 m.
- The Arks of the Plane between the Substylar and the Hour-lines, depending on the difference of Meridians, which is here 70 gr. 30 m. or 4 ho. 42 m. short of the Meridian, I first draw a Table with three Columns, one for the Morning and Evening Hours, another for the Angles at the Pole, and a third for the Arks of the Plane, and there write 70 gr. 30 m. by the Hour of 12, and place the Meridian and Substylar between the Hours of 7 and 8, according as the Poles of the Plane do fall in the Diagram.
| Latitude N. | 51 | 30 | |||
| Declinat. | 35 | 40 | |||
| Diff. Merid.. | 70 | 30 | |||
| Alt. Styl. | 14 | 41 | |||
| Dist. Subst. | 35 | 56 | |||
| Hours | Ang. Po. | Ar. Pla. | |||
| M. | E. | Gr. | M. | Gr. | M. |
| 2 | 10 | 79 | 30 | 54 | 12 |
| 3 | 9 | 64 | 30 | 28 | 16 |
| 4 | 8 | 49 | 30 | 16 | 42 |
| 5 | 7 | 34 | 30 | 10 | 0 |
| 6 | 6 | 19 | 30 | 5 | 11 |
| 7 | 5 | 4 | 30 | 1 | 9 |
| Merid. | Substyl. | ||||
| 8 | 4 | 10 | 30 | 2 | 43 |
| 9 | 3 | 25 | 30 | 6 | 58 |
| 10 | 2 | 40 | 30 | 12 | 21 |
| 11 | 1 | 55 | 30 | 20 | 28 |
| 12 | 70 | 30 | 35 | 56 | |
| 1 | 11 | 85 | 30 | 72 | 56 |
Then will the Angle at the Pole between the proper Meridian and the Hour of 11 be 55 gr. 30 m. the Hour of 10 will be 40 gr. 30 m. distant from the Meridian; and the rest in their order: which being noted in the second Column, the Ark of the Plane will be found to be such Numbers as I have noted in the third Column.
With this table thus made you may draw the Hour-lines, and set up the Style on either Face of this or the like Plane, the difference being only in the placing of the Substylar, and that is resolved by the sight of the Diagram.
A third Example, of a Plane falling near the Meridian.
After the like manner, if in our Latitude an upright Plane shall decline 85 gr. for the prime Vertical, the one Face of it being open to the North-west, and the other to the South-east, we may in some sort represent it by the Vertical QZH, and then working as before.
- The Angle ZPT, the Inclination of the two Meridians, will be found to be 86 gr. 5 m. so that PT the meridian of this Plane will here fall between the Hour-circles of 6 and 7 from the Meridian.
- The Ark PT, the measure of the Angle PCT, the height of the Pole above the Plane, will be 3 gr. 6 m.
- The Ark ZT, the measure of the Angle ZCT, the distance of the Substylar from the Meridian, 38 gr. 23 m.
- The Table of Angles at the Pole will be also gathered, by comparing the Meridian of the Plane with the rest of the Hour-circles: For the Angle TPZ, between TP the meridian of the Plane, PZ the meridian of the Place, and the Hour of 12, being 86 gr. 5 m. allowing 15 gr. for an Hour, the Hour of 11 ½ will be 78 gr. 35 m. and the Hour of 11, 71 gr. 5 m. distant from the Meridian of the Plane; and so the rest of the Hours. Or because the difference of Meridians 86 gr. 5 m. resolved into Time, makes 5 ho, 44 m. and so the Meridian of the Plane falls between the Hors of 6 and 7 from the Meridian. I first place this Meridian between these Hours, and then taking 75 gr. the common measure for 5 Hours, out of 86 gr 5 m. there remains 11 gr. 5 m. for the Angle at the Pole between the Meridian of the Plane and the Hour of 7. Again, I take 86 gr. 5 m. out of 90 gr. the common measure of 6 Hours, and there remains 3 gr. 55 m. for the Angle at the Pole between the Meridian of the Plane and the Hour of 6. To these Angles so found, I allow 15 gr. for every Hour, as in the second Column of this Table.
| Latitude N. | 51 | 30 | |||||||
| Declinat. | 85 | 0 | |||||||
| Diff. Merid.. | 86 | 5 | |||||||
| Alt. Styl. | 3 | 6 | |||||||
| Dist. Subst. | 38 | 23 | |||||||
| Hours | An. Po. | Ar. Pla. | C | I | C | G | |||
| Gr. | M. | Gr. | M. | I. | Par. | I. | Par. | ||
| 12 | 86 | 5 | 38 | 23 | 91 | 08 | 79 | 21 | |
| 78 | 35 | 15 | 3 | 30 | 92 | 26 | 89 | ||
| 11 | 71 | 5 | 9 | 6 | 18 | 42 | 16 | 02 | |
| 63 | 35 | 6 | 13 | 12 | 52 | 19 | 89 | ||
| 10 | 56 | 5 | 4 | 36 | 9 | 25 | 8 | 05 | |
| 9 | 41 | 5 | 2 | 42 | 5 | 43 | 4 | 72 | |
| 8 | 25 | 5 | 1 | 31 | 3 | 05 | 2 | 65 | |
| 7 | 11 | 5 | 0 | 30 | 1 | 20 | 1 | 05 | |
| Merid. | Substyl. | ||||||||
| 6 | 3 | 55 | 0 | 13 | 0 | 44 | 0 | 38 | |
| 5 | 18 | 55 | 1 | 4 | 2 | 15 | 1 | 80 | |
| 4 | 33 | 55 | 2 | 5 | 4 | 18 | 3 | 64 | |
| 3 | 48 | 55 | 3 | 33 | 7 | 13 | 6 | 20 | |
| 2 | 63 | 55 | 6 | 20 | 12 | 77 | 11 | 10 | |
| 71 | 25 | 9 | 10 | 18 | 56 | 16 | 18 | ||
| 1 | 78 | 55 | 15 | 28 | 31 | 82 | 27 | 67 | |
| 86 | 25 | 40 | 55 | 99 | 67 | 86 | 68 | ||
Then having the height of the Pole above the Plane, and these Angles at the Pole, the Arks of the Plane between the Substylar and the Hour-circles will be found as in the third Column.
These Arks being found, will serve for the drawing of the Hour-lines on either Face of this or like Plane.
- By the help of a Thred and Plummet I draw ZC a Vertical Line, serving both for the meridian of the place, and the Hour of 12.
- In this Meridian Line I make choice of a Center in the upper part of the Line, if it had been the Southern face of the Plane; but here in C the lower part of the Line, because we supposed it to be the North-west Face of the Plane, and the Style must point upward: and upon this Center I describe an occult Circle, representing the Declining vertical belonging to this Plane.
- I find a Chord of 38 gr. 23 m. the distance of the Substylar from the Meridian of the Place, and inscribe it into this Circle, from Z in the meridian, unto T toward the left hand, according as the proper Meridian PT falls in the Fundamental Diagram; and here I draw the Line CT serving for the Substylar.
- The Substylar being drawn, I may inscribe the Chords of the Arks of the Plane from the Substylar, and draw the Hour-lines, and set up the Style, as in the former Plane.
Or the Arks of the Plane from the Substylar being found as before, we may draw the Hour-line, upon the Plane otherwise than by Chords: For having drawn the Hour-lines as in the last Figure, upon paper or Pasteboard, we shall find the most part of them, in this and such like Planes that have greater Declination, to fall so close together, that they can hardly be discerned: wherefore to draw them at large to the best advantage of the Plane, I leave out the Center, and draw them by Tangents, as in the Polar Plane.
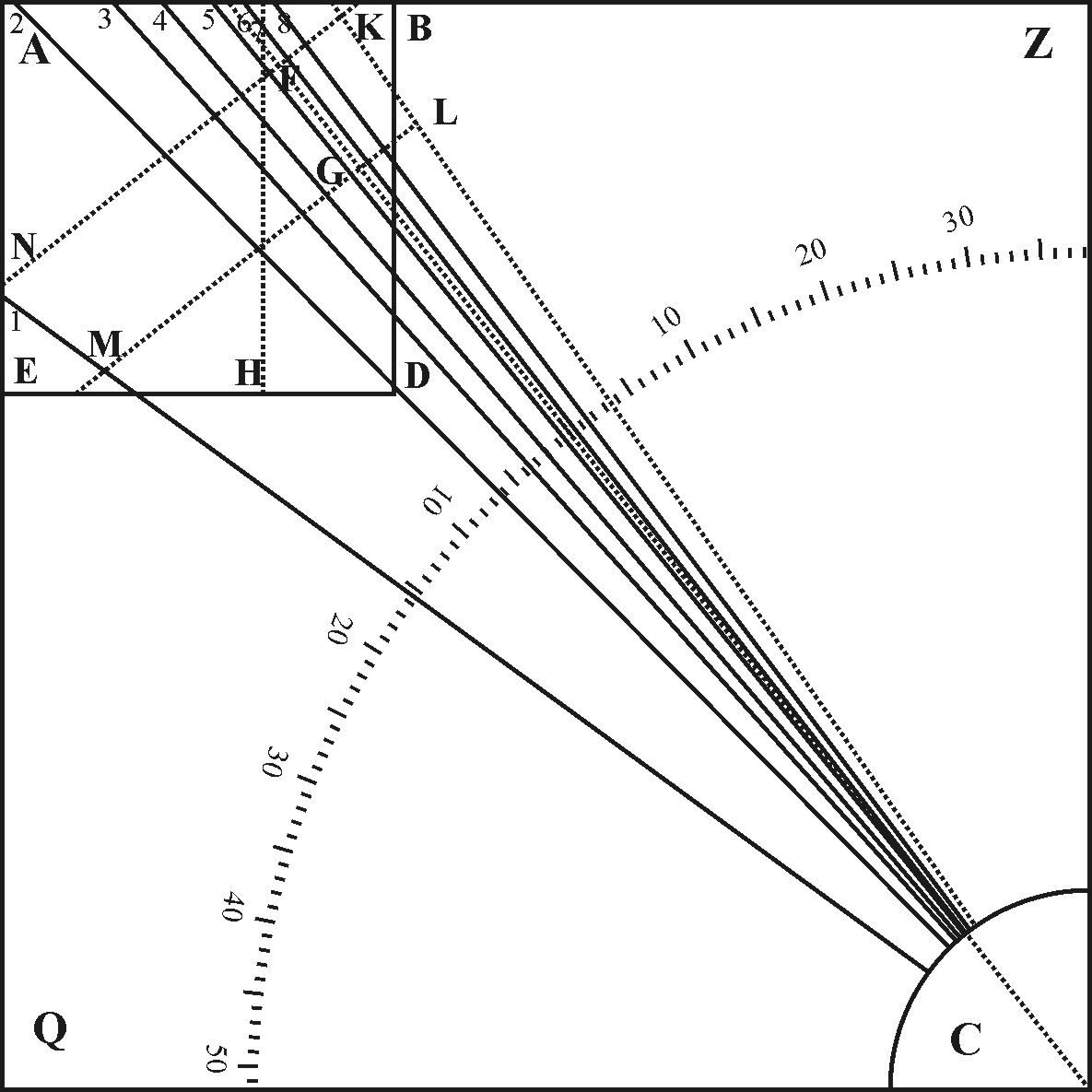
- I consider the length and breadth of the Plane whereon I am to draw the Hour-lines, which I suppose to be a Square whose Side is 36 Inches, and find that the little Square ABCD will contain both the Substylar and all those Hour-lines which are required in the great Square AZCQ.
- I draw two parallel Lines, FN, GM, crossing the Substylar at Right Angles in the points F and G, as they may best cross all the Hour-lines, and yet the one be distant from the other as far as the Plane will give me leave; and I find by the sight of the Figure, that if AB the Side of the lesser Square shall be 36 Inches, the Line CF will be about 115 Inches, and the Line CG about 100 Inches, and therefore FG 15 Inches. Again, that Point F will fall about 6 Inches below the upper Horizontal Side AB, and about 12 Inches from the Vertical Side BD; for I need not here stand upon parts.
- Because these two parallel Lines are tangent Lines, in respect of Circles drawn upon Semidiameters CF, CG, and such Tangent as belongs to the Arks of the Plane, being between the Substylar and the Hour-lines, the proportion will hold,
- As the Tangent of 45 gr. is to the tangent of the Ark of the Plane:
- So the Length of the Semidiameter, to the Length of the Tangent-line.
As for Example: The Ark of the Plane between the Substylar and the Hour of 1 is 15 gr. 28 m. in the former Table, the Semidiameter CF 115 Inches, and the Semidiameter CG 100 Inches: Wherefore I extend the Compasses from the Tangent of 45 gr. unto the tangent of 15 gr. 28 m. the same extent will reach from 115 in the Line of Numbers, unto 38,82, which shews the length of the tangent-line between F in the Substylar and the Hour-line of 1 to be 51 Inches 82 cent. or parts of 100. Again, the same extent will reach from 100 unto 27,67; and such is the length of the lesser Tangent from G unto the Hour of1.
The like reason holds for the length of the other Tangents from the Substylar to the rest of the Hours, as in the Table; as also for the height of the Style above these Tangent-lines: and so the Angle of the Style above the Plane being 3 gr. 6 m. the height FK will be found to be 6 Inches 23 cent. and the height GL 5 Inches 42 cent.
Where the Reader may observe, that if the extent from the Tangent of 45 gr. to the Tangent of 3 gr. 6 m. or to 115 in the Line of Numbers, be too large for his Compasses, he may use the Tangent of 5 gr. 43 m. instead of the Tangent of 45 gr. as I noted before.
- Having found these length and heights, and set them down in a Table, I come to the Plane here resembled by the lesser Square ABDE, where I begin with an occult Vertical FH, about 12 Inches from the Side BD, and upon the Center F, about 6 Inches below the Side AB, describe an occult Arks of a Circle.
- Into this Arks I first inscribe a Chord of 38 gr. 23 m. the distance of the Substylar from the Meridian, to make the Angle HFG equal to the Angle ZCT; so the Line FG shall be the Substylar: and then another Chord of 51 gr. 37 m. the Complement of this Distance, to make up the Right Angle GFN; so the Line FN shall be the greater of the two Tangent-lines before-mentioned.
- I set off 15 Inches from F unto G toward the Center, and through G draw the lesser Tangent-line GM, parallel to the former.
- These two occult Tangent-lines being this drawn, I look into the former Table for the Hour of 1, and there find the Ark of the Plane between the Substylar and the Hour of 1 to be 15 gr. 28 m. and the length belonging to the greater tangent-line to be 31 Inches 82 cent. in the lesser tangent-line 27 Inches 67 cent. wherefore I take out 31 Inches 82 parts, and prick them down in the greater tangent from F to N, and then 27 Inches 67 parts, and prick them down in the lesser tangent-line from G to M, and draw the Line MN for the Hour of 1, which if it were produced, would cross the Substylar FG in the center C, and there make the Angle FCN 15 gr. 28 m. The like Reason holdeth for the drawing of all the rest of the Hour-lines.
Lastly, I set up the Style right over the Substylar, so as the height FK may be 6 Inches 32 cent. and the Height GL 5 Inches 42 cent. then shall KL represent the Axis of the World, and if it were produced, would cross the Substylar FG in the center C, and there make the Angle FCH to be 3 gr. 6 m. and so be truly placed for casting of the Shadow upon the Hour-lines in this Declining Plane.