The Third Book of the Cross-Staff
CHAP. VIII.
To draw the Hour-lines in a Meridian Inclining Plane.
All Those Planes wherein the Horizontal Line is the same with the Meridian Line are therefore called Meridian Planes: if they be right to the Horizon, they are called by general name of Meridian Planes, without further addition, and are described before: if they lean to the Horizon, they are called Meridian Incliners.
These may incline either to the East part of the Horizon, or to the West, and each of them hath two Faces, the upper toward the Zenith, the lower towards the Nadir, wherein knowing the Latitude of the Place, and the Inclination of the Plane to the Horizon, we are to consider,
- The Inclination of the Meridian of the Plane to the Meridian of the Place.
- The Height of the Pole above the Plane.
- The Distance of the Substylar from the Meridian.
- The Distance of each Hour-line from the Substylar.
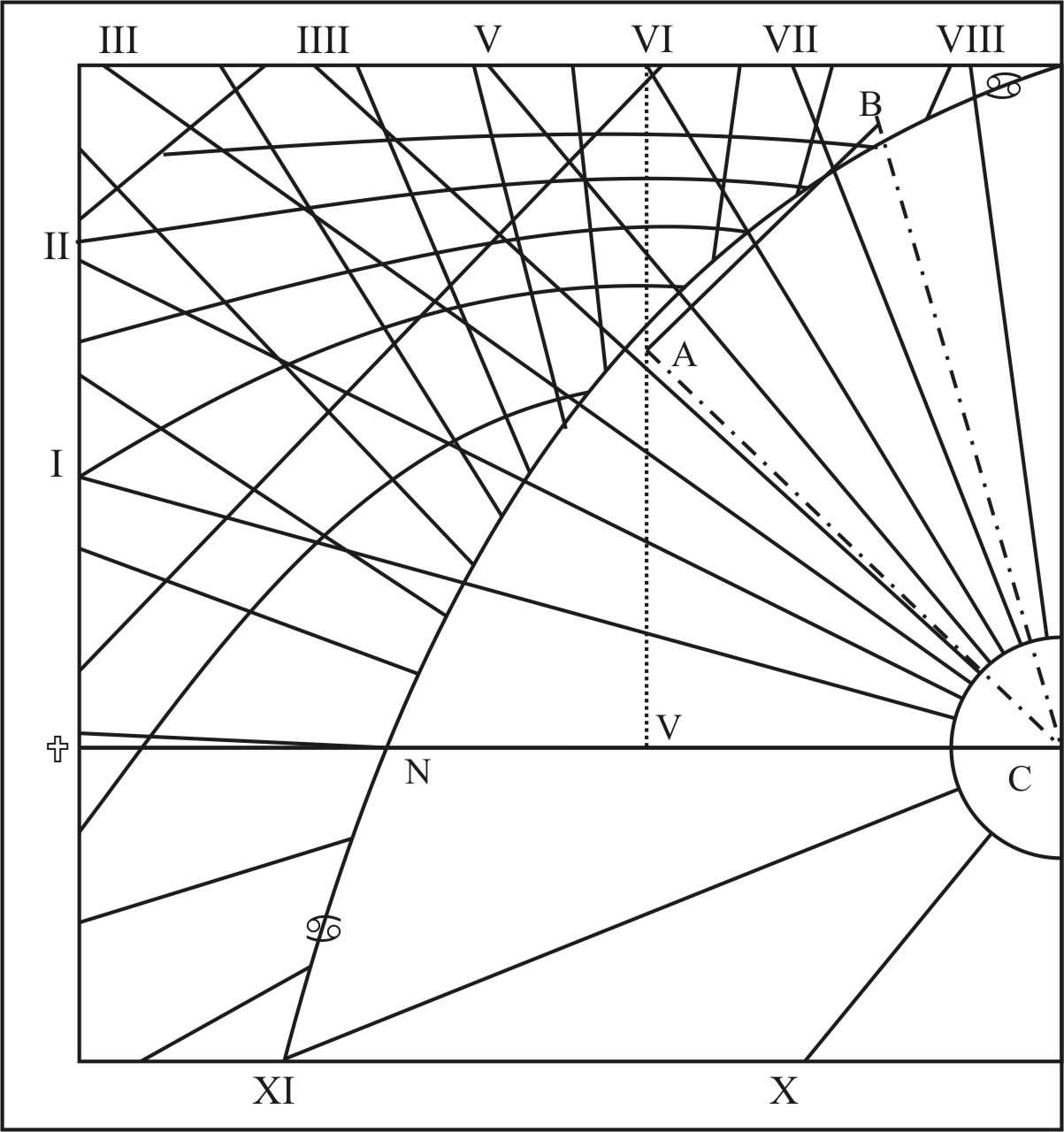
And all these four are represented in the Fundamental Diagram, as in this Example.
In our Latitude of 51 gr. 30 m. a Meridian Plane inclineth Eastward 50 gr. these 50 gr. I number in the vertical Circle from E unto G, according to the Inclination of the Plane, and there draw the Ark SGN representing the Plane proposed. Again, I number 50 from Z unto K, so the Point K (being 90 gr. from the Plane at G) shall be the Pole of this Plane, and the proper Meridian of this Plane may be supplied by a Circle drawn through K and P. This Meridian doth here fall between the Hours of 4 and 5, and crossing the Plane at Right Angles in the Point V, in the Right Line VC shall be the Substylar, and the Angle PCV the height of the Style above the Plane, and Right Lines drawn from the center C to the Intersections of the Hour-circles with SGN shall be the Hour-lines here inquired. The lower Face of the Plane will contain all the Hour-lines from Sun-rising unto 11 in the Morning, and the upper Face the Hours from 9 in the Morning unto Sun-setting. Then have I a Rectangle Triangle PVN, wherein the Base PN is the Height of the Pole above the North part of the Horizon, and the Angle PNV the Complement of the Inclination to the Horizon: and these being known,
- I may find the Angle NPV of Inclination of the two Meridians: For,
- As the Cosine of the Latitude, is to the Sine of 90 gr.
- So the Tangent of the Inclination to the Horizon, to the Tangent of Inclination of Meridians.
Extend the Compasses from the Sine of 38 gr. 30 m. the Complement of the Latitude, unto the Sine of 90 gr. the same extent will reach from the Tangent of 50 gr. 0 m. the Inclination of the Plane to the Horizon, unto the Tangent of 62 gr. 25 m. and such is the Inclination of the Meridian of the Plane to the Meridian of the Place; which being resolved into Time, doth give about 4 ho. and 10 m. from the Meridian, for the place of the Substylar among the Hour-lines.
- The Height of the Pole above the Plane is here represented by the quantity of the Ark of the proper Meridian PV, between the Pole and the Plane, and may be known by that which we have given in the former Triangle PVN. For,
- As the Sine of 90 gr. to the Sine of the Latitude:
- So the co-sine of the Inclination to the Horizon, to the Sine of the height of the Pole above the Plane.
Extend the Compasses from the Sine of 90 gr. unto 51 gr. 30 m. the Sine of the Latitude, the same extent will reach from the Sine of 40 gr. the Complement of the Inclination of the Plane to the Horizon, unto the Sine of 30 gr. 12 m. Or,
- As the Sine of 90 gr. to the Co-sine of the Inclination of Meridians:
- So the Tangent of the latitude, to the Tangent of the Height of the Pole above the Plane.
Extend the Compasses from the Sine of 90 gr. unto the Tangent of 51 gr. 30 m the latitude of the Place, the same extent will reach from the Sine of 27 gr. 35 m. the Complement of the Inclination of the two Meridians, unto the Tangent of 30 gr. 12 m. And such is PV the Height of the Pole above the Plane, and such must be the Height of the Style above the Substylar.
- The Distance of the Substylar from the Meridian is here represented by NV the Ark of the Plane between the two Meridians, and may be found by that which we have given at the first in the former Triangle PVN. For,
- As the Sine of 90 gr. to the Sine of the Inclination to the Horizon:
- So the Tangent of the Latitude, to the Tangent of the Substylar from the Meridian.
Extend the Compasses from the Sine of 90 gr. unto the Tangent of 51 gr. 30 m. the Latitude of the Place, the same extent will reach from the Sine of 50 gr. the Inclination of the Plane to the Horizon, unto the Tangent of 43 gr. 55 m. And such is the Ark NV, the distance of the Substylar from the Meridian.
- The Distances of te Hour-lines from the Substylar are here also represented by those Arks of the Plane which are here intercepted between the proper Meridian and the Hour-circles, and may be found by that which we have given in the Triangles made by the Plane, with his proper Meridian and the Hour-circles: For the Angle at V, between the Plane and the proper Meridian, is well known to the a Right Angle, and the Side PV is the height of the Pole above the Plane, and the Angles at the Pole between the proper Meridian and the Hour-circles are easily gathered into a Table. The Angle VPN between VP the proper Meridian of the Plane, and PN the general Meridian of the Place, being 62 gr. 25 m. the Angle between the proper Meridian and the Circle of the Hour of 11 will be 77 gr. 25 m. and the Angle belonging to the Hour of 1, 47 gr. 25 m. and the rest of the Angles at the Pole. Then,
- As the Sine of 90 gr. to the Sine of the height of the Pole above the Plane:
- So the Tangent of the Angle at the Pole, to the Tangent of the Hour-line from the Substylar.
Wherefore I extend the Compasses from the Sine of 90 gr. unto the Sine of 30 gr. 12 m. the Height of the Pole above the Plane, and find the same extent to reach in the Line of Tangents from 77 gr. 25 m. unto 66 gr. 4 m. for the distance belonging to the hour of 11; and from the tangent of 62 gr. 25 m. to 43 gr. 55 m. for the Hour of 12, as when I found the distance of the Substylar from the Meridian: And so for the rest of the Arks of the Plane between the Substylar and the Hour-circles, as in the Table.
| Latitude | 51 | 30 |
| Inclinat. | 50 | 0 |
| Diff.Merid. | 62 | 25 |
| Alt.Styl. | 30 | 12 |
| Dist.Subst. | 43 | 55 |
| Hours | >Ang. Po. | Ar. Pla. | ||
| Gr. | M. | Gr. | M. | |
| 11 | 77 | 25 | 66 | 4 |
| 12 | 62 | 25 | 43 | 55 |
| 1 | 47 | 25 | 28 | 41 |
| 2 | 32 | 25 | 17 | 43 |
| 3 | 17 | 25 | 8 | 58 |
| 3 | 2 | 25 | 1 | 13 |
| Merid. | Substyl. | |||
| 5 | 13 | 35 | 6 | 26 |
| 6 | 27 | 35 | 14 | 44 |
| 7 | 42 | 35 | 24 | 48 |
| 8 | 57 | 35 | 38 | 23 |
| 9 | 72 | 35 | 58 | 3 |
| 10 | 87 | 31 | 85 | 12 |
These Arks being thus found, will serve to draw the Hour-lines on either Side of this Plane: But supposing it to be the upper side,
- I draw the Horizontal Line CN, serving for the Meridian and Hour of 12.
- In this Line I make choice of the Center at C, and thence describe an occult Ark of a Circle representing the Plane proposed.
- I find a Chord of 43 gr. 55 m. the distance of the Substylar from the Meridian, and inscribe it into this Circle from N unto A, according as I find the proper Meridian PV to fall in the Fundamental Diagram, and there I draw the Line CA serving for the Substylar.
- The Substylar being drawn, I may inscribe the Chords of the Arks of the Plane from the Substylar, and draw the Hour-Lines, and set up the Style, as in the former Planes.