The Third Book of the Cross-Staff
CHAP. X.
To draw the Hour-lines in a Declining Inclining Plane.
If a Plane shall decline from the prime Vertical, and incline to the Horizon, and yet not lie even with the Poles of the World, it is then called a Declining Inclining Plane.
Of these there are several sorts; for the Inclination Northward, the Plane may fall between the Horizon and the Pole, as the Circle BMD in the Fundamental Diagram; or between the Zenith and the Pole, as BFD; or the Inclination may be Southward, and so be represented by BRD; it may also fall either below the Intersection of the Meridian and the Equator, or above it; and each of these hath two Faces, the upper toward the Zenith, and the lower toward the Nadir; wherein having the Latitude of the Place, with the Declination and Inclination of the Plane, we are further to consider,
- The Ark of the Meridian between the Pole and the Plane.
- The Inclination of the Plane to the Meridian.
- The Ark of the Plane between the Horizon and the Meridian.
- The Angle of Inclination between both Meridians.
- The Height of the Pole above the Plane.
- The distance of the Substylar from the Meridian.
- The distance of each Hour-line from the Substylar.
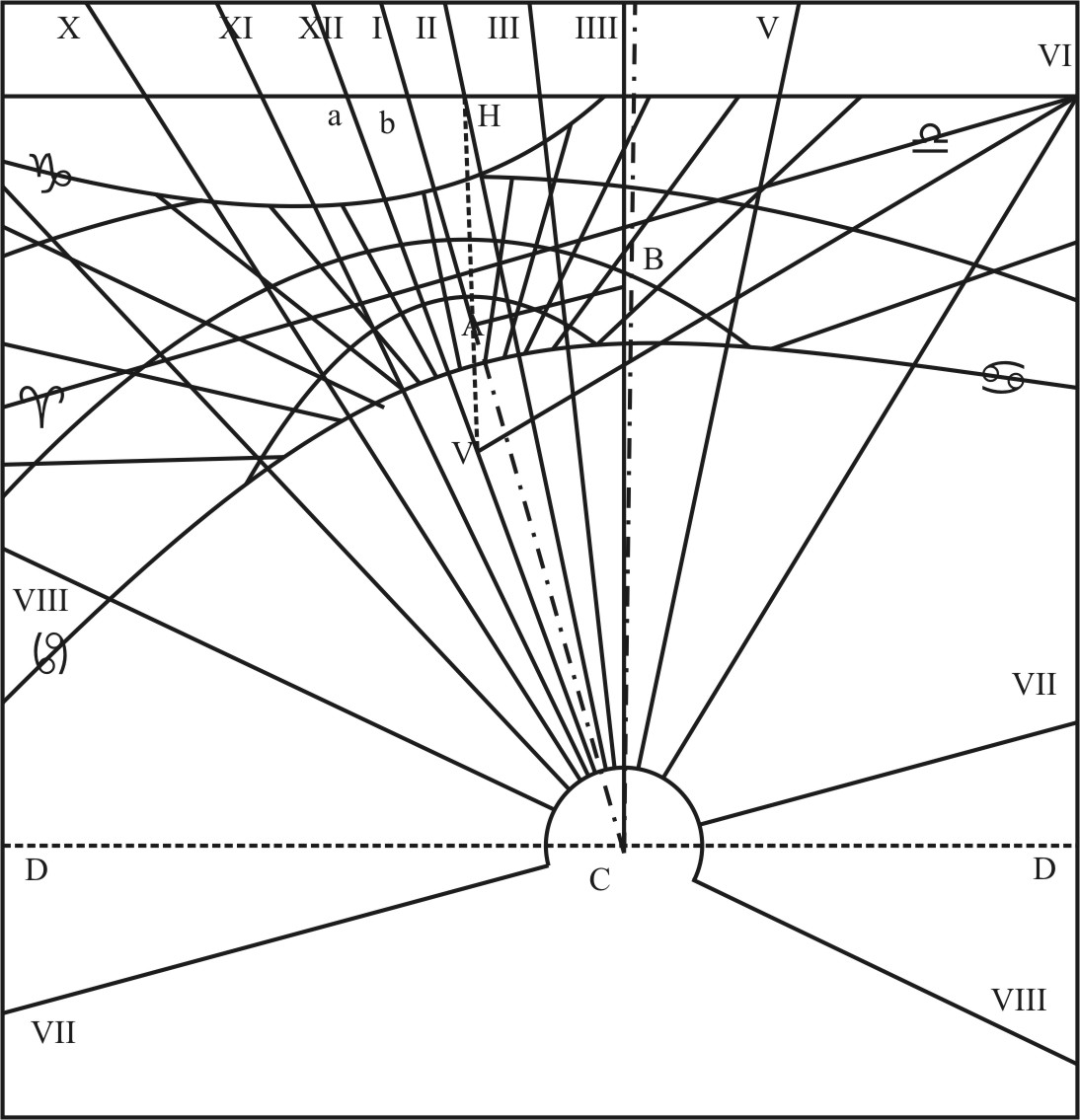
And all these seven may be represented in the Fundamental Diagram, as in this Example.
In our Latitude of 51 gr. 30 m. a Plane is proposed declining from the Vertical 24 gr. 20 m. and inclining Northward 36 gr. the upper face lying open to the South-west, the lower to the North-east. If I number these 24 gr. 20 m. in the Horizon from E to B, and there draw the Line BCD, it shall represent the Horizontal Line of the Plane: Then crossing it at Right Angles with the Plane HZQ drawn through the Zenith, I number 36 gr. for the Inclination from Q unto M, and there draw the Circle BMD, crossing the Meridian in the Point a; this Circle so drawn shall represent the Plane proposed: and because it doth not pass through the Pole, is therefore no Polar, but an ordinary Declining Inclining Plane.
- The Ark of the Meridian of the Place between the Pole and the Plane is here represented by Pa, and may be found by resolving the Triangle DNa, wherein the Angle at N is known to be a Right Angle, the Angle at D is the Angle of Inclination, the Side DN the Complement of the Declination; which being known,
- As the Sine of 90 gr. to the Cosine of Declination:
- So the Tangent of Inclination to the Horizon, to the Tangent of the Ark of the Meridian between the Horizon and the Plane.
Extend the Compasses from the Sine of 90 gr. unto the Sine of 65 gr. 40 m. the Complement of the Declination, the same extent will reach from the Tangent of 36 gr. the Inclination proposed, unto the Tangent of 33 gr. 30 m. and such is the Ark of the Meridian Na between the Horizon and the Plane. This Ark Na being compared with the Ark NP, which is the Elevation of the Pole above the Horizon, and is here supposed to be 51 gr. 30 m. the difference Na cometh to 18 gr. and such is the Ark of the Meridian required between the Pole and the Plane.
- The Inclination of the Plane to the Meridian is here represented by the Angle NaD, and may be found by that which we have given in the former Triangle DNa. For,
- As the Sine of 90 gr. to the Sine of the Declination from the Vertical:
- So the Sine of the Inclination to the Horizon, to the Co-sine of Inclination of the Plane to the Meridian.
Extend the Compasses from the Sine of 90 gr. unto the Sine of 24 gr. 20 m. the Declination of the Plane, the same extent will reach from the Sine of 36 gr. the Inclination given, unto the Co-sine of 76 gr. and such is NaD the Angle of Inclination between the Plane Da and Na the Meridian of the Place. Or,
- As the Sine of the Ark of the Meridian between the Horizon and the Plane, is to the Sine of 90 gr.
- So the Co-tangent of the Declination, to the Tangent of Inclination of the Plane to the Meridian.
Extend the Compasses from the Sine of 33 gr. 30 m. the Ark of the Meridian between the Horizon and the Plane, unto the Sine of 90 gr. the same extent will reach from the Tangent of 65 gr. 40 m. the Complement of the declination, unto the Tangent of 67 gr. and such is the Inclination of the Plane to the meridian, the same as before.
- The Ark of the Plane between the Horizon and the Meridian is here represented by Da, and may also be found by that which we have given in the former Triangle DNa.
- As the Co-sine of Inclination to the Horizon, is to the Sine of 90 gr.
- So the Co-tangent of the declination, to the Tangent of the Ark of the Plane from the Horizon to the Meridian.
Extend the Compasses from the Sine of 54 gr. the Complement of the Inclination of the Plane to the Horizon, unto the Sine of 90 gr. the same extent will reach from the tangent of 65 gr. 40 m. the Complement of the Declination, unto the Tangent of 69 gr. 54 m. And such is Da the Ark of the Plane between the Horizon and the Meridian of the Place.
- The Inclination of Meridians is here represented by the Angle abP. For having drawn the proper Meridian bPk, or let down a Perpendicular Pb from the Pole unto the Plane, this Perpendicular shall be the Meridian of the Plane, and we shall have another Triangle abP, wherein the Angle at b is a Right Angle because of the Perpendicular, the Angle at a is the Inclination of the Plane to the Meridian of the Place, and the Side Pa is the Ark of the Meridian between the Pole and the Plane; which being known,
- As the Co-sine of the Ark of the Meridian between the Pole and the Plane, is to the Sine of 90 gr.
- So the Co-tangent of the Inclination of the Plane to the Meridian, to the Tangent of Inclination of the Meridian of the Plane to the Meridian of the Place, that is, the Angle at the Pole between the two Meridians.
Extend the Compasses from the Sine of 72 gr. the Complement of the Ark Pa between the Pole and the Plane, unto the Sine of 90 gr. the same extent will reach from the Tangent of 14 gr. the Complement of the Inclination of the Plane to the Meridian, unto the Tangent of 14 gr. 41 m. And such is the Angle aPb of Inclination between the Meridians of the Place and the proper Meridian of the Plane; which resolved into Time, doth make about 59 m. and so the Substylar must here be placed near the Hour of 1 after Noon.
- The Height of the Pole above the Plane is here represented by Pb the Ark of the proper meridian between the Pole and the Plane, and may be found by that which we have given in the Triangle abP. For,
- As the Sine of 90 gr. to the Sine of the Ark of the Meridian of the Place between the Pole and the Plane:
- So the Sine of Inclination of the Plane to the Meridian, to the Sine of the Height of the Pole above the Plane.
Extend the Compasses from the Sine of 90 gr. unto the Sine of 18 gr. the Ark Pa of the Meridian of the Place from the Pole to the Plane, the same extent will reach from the Sine of baP the Inclination of the Plane to the Meridian of the Place, unto the Sine of 17 gr. 26 m. Or,
- As the Sine of 90 gr. to the Co-sine of Inclination of Meridians:
- So the Tangent of the Ark of the Meridian of the Place between the Pole and the Plane, to the Tangent of the Height of the Pole above the Plane.
Extend the Compasses from the Sine of 90 gr. unto the Sine of 75 gr. 19 m. the Complement of aPb the Inclination of the two Meridians, the same extent will reach from the Tangent of 18 gr. the Ark Pa of the general Meridian between the Ple and the Plane, unto the Tangent of 17 gr. 26 m. And such is Pb the Height of the Pole above the Plane; and such must be the Height of the Style above the Substylar.
- This Distance of the Substylar from the Meridian of the Place is here represented by ab the Ark of the Plane between the two Meridians, and may be found by that which we had given at the first former Triangle abP. For,
- As the Sine of 90 gr. to the Cosine of the Inclination of the Plane to the Meridian:
- So the Tangent of the Ark of the Meridian of the Place between the Pole and the Plane, unto the Tangent of the Substylar from the Meridian of the Place.
Extend the Compasses from the Sine of 90 gr. unto the Sine of 14 gr. the Complement of baP the Inclination of the Plane to the Meridian, the same extent will reach from the Tangent of 28 gr. the Ark of the general Meridian between the Pole and the Place, unto the Tangent of 4 gr. 30 m. And such is the Ark of the Plane between the two Meridians; and such must be the Distance from the Hour of 12 to the Substylar.
- The Distances of the Hour-lines from the Substylar are here represented by those Arks of the Plane which are intercepted between the proper Meridian and the Hour-circles: For in these Triangles, the Angle at b between the Plane and the proper Meridian is a Right Angle, the Side Pb is the Height of the Pole above the Plane, and then the Angles at the Pole between the proper Meridian and the Hour-circles being gathered into a Table,
- As the Sine of 90 gr. to the Sine of the Height of the Pole above the Plane:
- So the Tangent of the Angle at the Pole, to the Tangent of the Hour-line from the Substylar.
Latitude 51 30 Declinat. 24 20 Inclin. N. 36 0 Alt. Merid. 69 54 Diff. Merid. 14 41 Alt. Styl. 17 26 Dist. Subst. 4 30 Hours Ang. Po. Tang. Gr. M. In. Par. 7 89 41 88 57 8 74 41 47 35 9 59 41 27 9 10 44 41 16 31 11 29 41 9 41 12 14 41 4 30 Merid. Substyl 1 0 19 0 6 2 15 19 5 4 3 30 19 9 56 4 45 19 6 52 5 60 19 7 45 6 75 19 48 51 Extend the Compasses from the Sine of 90 gr. unto the Sine of 17 gr. 26 m. the Height of the Pole above the Plane, the same extent will reach from the Tangents of 14 gr. 41 m. the Angle at the Pole belonging to the Hour of 12, unto the Tangent of 4 gr. 30 m. for the Ark of the Plane between the Substylar and the Hour of 12; and from the Tangent of 29 gr 41 m. unto the Tangent of 9 gr. 41 m. for the Hour of 11: And so the rest of the Arks of the Plane between the Substylar and the Hour-lines, as in the former Table.
These Arks being thus found, will serve for the drawing of the Hour-lines on either side of the Plane: but supposing it to be the upper side, I consider how the Lines do fall in the Fundamental Diagram, and accordingly,
- First, I draw an occult Horizontal Line DD, wherein I make choice of the Center C, and hence draw and occult Circle for the Horizon of the Plane.
- I find a Chord of 69 gr. 54 m. the Ark of the Plane between the Horizon and the Meridian, and describe it into this Circle from D unto a, and there draw the Line Ca for the Hour of 12.
- I find a Chord of 4 gr. 30 m. the Ark of the Plane between the two Meridians, and inscribe it into this Circle from a unto b, and there draw the Line Cb for the Substylar.
- The Substylar being drawn, I may inscribe the Chords of the Axis of the Plane from the Substylar, and draw the Hour-lines, and set up the Style, as in the former Plane.
A second Example of a Plane falling between the Pole and the Zenith.
In like manner if in our Latitude a Plane be proposed declining from the Vertical 24 gr. 20 m. as before, but inclining to the Horizon 75 gr. 40 m. Northward, the upper Face being open to the South-west, the lower to the North-east, this Plane shall be here represented by the Circle BFD, crossing the Meridian in the point d, between the Pole and the Zenith, and the proper Meridian of this Plane, by the Perpendicular Ark Pa.
Then in this Triangle DNd knowing the Side DN, the Complement of the Declination, with the Angle of Inclination to the Horizon at D, and the Right Angle at N, these former Canons will give Nd, the Ark of the Meridian between the Horizon and the Plane, to be 74 gr. 20 m. and therefore PD, the Ark of the Meridian between the Pole and the Plane, will be 22 gr. 50 m. the Angle DdN of Inclination of the Plane to the Meridian will be found to be 66 gr. 29 m. and Dd the Ark of the Plane between the Horizon and the Meridian 83 gr. 36 m.
| Latitude | 51 | 30 | ||
| Declinat. | 24 | 20 | ||
| Inclin. | 75 | 40 | ||
| Alt. Merid. | 83 | 36 | ||
| Diff. Merid. | 25 | 17 | ||
| Alt. Styl. | 20 | 50 | ||
| Dist. Subst. | 9 | 32 | ||
| Hours | Ang. Po. | Tang. | ||
| Gr. | M. | In. | Par. | |
| 8 | 85 | 17 | 76 | 56 |
| 9 | 70 | 17 | 44 | 47 |
| 10 | 55 | 17 | 27 | 11 |
| 11 | 40 | 17 | 16 | 43 |
| 12 | 25 | 17 | 9 | 32 |
| 1 | 19 | 17 | 9 | 41 |
| Merid. | Substyl | |||
| 2 | 4 | 43 | 1 | 40 |
| 3 | 19 | 43 | 7 | 16 |
| 4 | 34 | 43 | 13 | 50 |
| 5 | 49 | 43 | 22 | 46 |
| 6 | 64 | 43 | 37 | 0 |
| 7 | 79 | 43 | 62 | 5 |
Again, in the Triangle Ped, knowing the Side Pd, the Ark of the Meridian between the Pole and the Plane, with the Angle of Inclination to the Meridian at d, and the Right Angle at e, the Angle dPe of the Inclination of the two Meridians will be found to be 25 gr. 17 m. and Pe the Height of the Pole above the Plane to be 20 gr. 50 m. and de the distance of the Substylar from the Meridian about 9 gr. 32 m. Lastly, having found the Height of the Pole above the Plane, and gathered the Angles at the Pole, the Arks of the Plane from the Substylar to the Hour-lines will be as in the Table.
This done, if we consider how the Lines do fall in the Fundamental Diagram, we may there see how the North Pole is elevated above the lower face, and the South Pole above the upper Face of the Plane, and accordingly make choice of a Center, draw the Horizontal, the Meridian, the Substylar, and the Hour-lines, and set up the Style, as in the other Planes.
A third Example of a Plane inclining to the Southward.
If in our Latitude a Plane were proposed declining from the Vertical 24 gr. 20 m. as before, but inclining to Horizon 14 gr. 20 m. Southward, the upper Face being open to the North-east, the lower to the South-west, this Plane shall be there represented by the Circle BKD, crossing the Meridian in the point f, between the Equator and the Horizon, and the proper Meridian of this Plane, by the perpendicular Ark Pg, let down from the Pole to the Plane, near the Hour of 11, at the North part of the Horizon, as may partly appear by the nearest extent of the Compasses, if the Circle BKD were drawn round, and the two Letters f and g supplied.
Then in the Triangle BSf, knowing the Side BS the Complement of the Declination, with the Angle of Inclination to the Horizon at B, at the Right Angle at S, we may find Sf the Ark of the Meridian between the Horizon and the Plane to be 13 gr. 6 m. And therefore Pf, the Ark of the Meridian between the Pole and the Plane to the Southward 115 gr. 24 m. but 64 gr. 36 m. to the Northward, the Angle BfS, or DfN of the Inclination of the Plane between the Horizon and the Meridian 66 gr. 20 m.
Again, in the Triangle Pgf, knowing the Side Pf the Ark of the Meridian between the Pole and the Plane, with the Angle of Inclination to the Meridian at f, and the Right Angle at g, the Angle fPg of the Inclination of the two Meridians will be found to be 13 gr. 27 m. and Pg the Height of the Pole above the Plane, about 64 gr. and fg the Distance of the Sunstylar from the Meridian 12 gr. 8 m.
Having found the Height of the Pole above the Plane, and gathered the Angles at the Pole, the Arks of the Plane from the Substylar to the Hour-lines will be found as in the Table.
This done, if we consider how the Lines do fall in the Fundamental Diagram, we may there see how the North Pole is elevated above the upper Face, and the South Pole above the lower Face of this Plane; and accordingly make choice of the Center, draw the Horizontal, the Meridian, the Substylar, and the Hour-lines, and set up the Style, as in the former Planes.
| Latitude | 51 | 30 | ||
| Declinat. | 24 | 20 | ||
| Inclin. | 14 | 20 | ||
| Alt. Merid. | 66 | 20 | ||
| Diff. Merid. | 13 | 27 | ||
| Alt. Styl. | 64 | 0 | ||
| Dist. Subst. | 64 | "= | ||
| Hours | Ang. Po. | Tang. | ||
| Gr. | M. | In. | Par. | |
| 6 | 76 | 33 | 76 | 56 |
| 7 | 61 | 33 | 58 | 56 |
| 8 | 46 | 33 | 43 | 30 |
| 9 | 31 | 33 | 18 | 55 |
| 10 | 16 | 33 | 14 | 58 |
| 11 | 1 | 33 | 1 | 25 |
| Merid. | Substyl | |||
| 12 | 13 | 27 | 12 | 8 |
| 1 | 28 | 27 | 15 | 57 |
| 2 | 43 | 27 | 40 | 23 |
| 3 | 58 | 27 | 55 | 38 |
| 4 | 73 | 27 | 71 | 41 |
| 5 | 88 | 27 | 82 | 15 |