The Third Book of the Cross-Staff
CHAP. XII.
To describe the Tropicks and other Circles of Declination in a Polar Plane.
In all Polar Planes, whether they be parallel to the Meridian, or to the Circles of the Hour of 6, or otherwise declining, the Equinoctial will be a Right Line, but the Tropicks and other Circles of Declination will be Sections Hyperbolical, and be thus described.
Consider the length of the Style, the Declination of the Parallel, and the Angle at the Pole between the Substylar and the Hour-line, whereon you mean to describe the Parallel.
If you would find where the Parallels do cross the Substylar,
- As the Tangent of 45 gr. to the Tangent of Declination:
- So is the length of the Style, to the Distance of the Parallel from the Equinoctial.
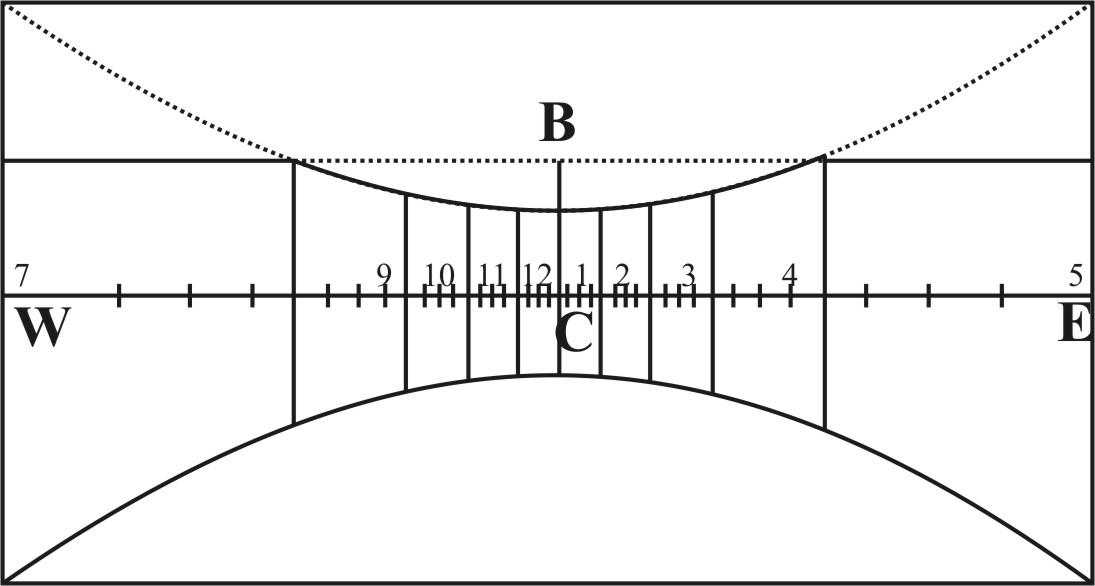
As in the Example of the Polar Plane, where the length of the Style BC was found to be 1 Inch 61 cent. If you desire to know the distance between the Equinoctial and the Tropick upon the Substylar Line, extend the Compasses from the Tangent of 45 gr. unto the Tangent of 23 gr. 30 m. the same extent will reach in the Line of Numbers from 1.61 unto 0.70; and therefore the distance required is 70 parts of an Inch divided into 100. The like reason holdeth for all other Parallels of Declination crossing the Substylar.
But if you would find where the parallels do cross any other of the Hour-lines, first find the Distance between the Axis of the Style and the Hour-line, then the distance between the Equinoctial and the Parallel: Both these may be represented in this manner.
On the Center B, and any Semidiameter BD, describe an occult Ark of a Circle, and therein inscribe a Chord of 23 gr. 30 m. from D unto T, with such other intermediate Declination as you intend to describe on the Plane; so the Line BD shall be the Equator, and BT the Tropick, and the other intermediate Lines the Lines of Declination.
That done, consider your Plane, which for example may be either the Meridian or the Declining Polar Plane; wherein having drawn both the Equator and the Hour-lines as before, first take out the Height of the Style, and prick that down in this Equator from B unto C; then taking out all Distances between B the top of the Style, and the several Points wherein the Hour-lines do cross the Equator, transfer them into the Equator BD from the Center B, and at the terms of these Distances erect Lines perpendicular to the Equator, crossing the Lines of Declination, and note them with the Numbers of the Hour from whence they were taken: so these Perpendiculars shall represent those Hour-lines, and the several Distances between the Equator and the Lines of Declination shall give the like Distances between the Equator and the Parallels of declination upon your Plane. Upon this ground it followeth,
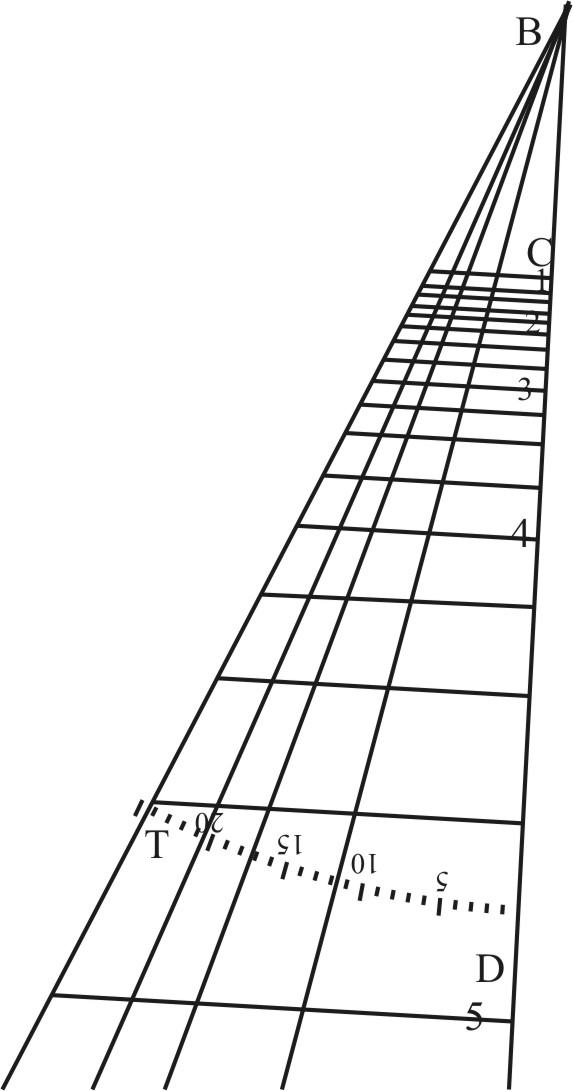
To find the distance between the Axis and the Hour-lines.
- As the Co-sine of the Hour from the Substylar, is to the Sine of 90 gr.
- So the length of the Style, to the distance between the Axis and the Hour-line.
As if in the former Example of the meridian Plane, where BC the height of the Style is supposed to be 10 Inches, it were required to find the distance between B to the top of the Style, and the point wherein the Hour of 11 in the Morning doth cross the Equator, which is here represented by B5, because it is the fifth Hour from the Substylar, whose Angle at the Pole is 75 gr. Extend the Compasses from the Sine of 15 gr. the Complement of the fifth Hour from the Substylar, unto the Sine of 90 gr. the same extent will reach from 10.00 in the Line of Numbers, unto 38.64; and therefore the distance B5, between the Axis and the Hour-line, is 38 Inches and 64 cent. and may be called the Secant of the Hour. Then in the Rectangle B5T, having the Side B5, and the Angle of Declination at B,
To find the distance between the Equinoctial and the Parallel.
- As the Tangent of 45 gr. to the Tangent of the Declination,
- So the distance between the Axis and the Hour-line, to the distance between the Equinoctial and the Parallel.
Extend the Compasses from the Tangent of 45 gr. unto the Tangent of 23 gr. 30 m. the Declination of the Tropick, so the same extent will reach in the Line of Numbers from 38.64 the distance between the Axis and the fifth Hour-line, unto 16.80; and therefore the distance is 16 Inches and 80 cent. The like reason holdeth for all the rest, which may be gathered, and set down in such a Table as this which followeth.
Wherein I have set down the Distances for several Declinations, for 11 gr. 30 m. for 16 gr. 55 m. for 20 gr. 12 m. for 21 gr. 41 m. and for the Declination of the Tropick 23 gr. 30 m. which may be applied to the like Declinations in all Meridian and direct Polar Planes.
| Ho. | An. Po. | Tang. | Secant. | 11 30 | 16 55 | 20 12 | 21 41 | 23 30 | ||||||||
| Gr. | M. | In. | Pa. | In. | Pa. | In. | Pa. | In. | Pa. | In. | Pa. | In. | Pa. | In. | Pa. | |
| 0 | 0 | 0 | 0 | 0 | 10 | 00 | 2 | 3 | 3 | 4 | 3 | 68 | 3 | 98 | 4 | 35 |
| 3 | 45 | 0 | 65 | 10 | 02 | 2 | 04 | 3 | 05 | 3 | 69 | 3 | 99 | 4 | 36 | |
| 7 | 30 | 1 | 32 | 10 | 09 | 2 | 05 | 3 | 07 | 3 | 71 | 4 | 01 | 4 | 39 | |
| 11 | 15 | 1 | 99 | 10 | 20 | 2 | 07 | 3 | 10 | 3 | 75 | 4 | 05 | 4 | 43 | |
| 1 | 15 | 0 | 2 | 68 | 10 | 35 | 2 | 10 | 3 | 15 | 3 | 81 | 4 | 12 | 4 | 50 |
| 18 | 45 | 3 | 39 | 10 | 56 | 2 | 15 | 3 | 21 | 3 | 99 | 4 | 20 | 4 | 59 | |
| 22 | 50 | 4 | 14 | 10 | 82 | 2 | 20 | 3 | 29 | 4 | 10 | 4 | 30 | 4 | 70 | |
| 26 | 15 | 4 | 93 | 11 | 15 | 2 | 36 | 3 | 39 | 4 | 24 | 4 | 45 | 4 | 85 | |
| 2 | 30 | 0 | 5 | 77 | 11 | 55 | 2 | 34 | 3 | 51 | 4 | 60 | 5 | 02 | ||
| 33 | 45 | 6 | 68 | 12 | 03 | 2 | 44 | 3 | 66 | 4 | 42 | 4 | 78 | 5 | 21 | |
| 37 | 30 | 7 | 67 | 12 | 60 | 2 | 56 | 3 | 83 | 4 | 64 | 5 | 02 | 5 | 48 | |
| 41 | 15 | 8 | 77 | 13 | 30 | 2 | 70 | 4 | 05 | 4 | 89 | 5 | 29 | 5 | 78 | |
| 3 | 45 | 0 | 10 | 00 | 14 | 14 | 2 | 87 | 4 | 30 | 5 | 10 | 5 | 63 | 6 | 15 |
| 48 | 45 | 11 | 40 | 15 | 17 | 3 | 08 | 4 | 62 | 5 | 58 | 6 | 03 | 6 | 00 | |
| 52 | 30 | 13 | 03 | 16 | 43 | 3 | 34 | 5 | 00 | 6 | 04 | 6 | 54 | 7 | 14 | |
| 56 | 15 | 14 | 97 | 18 | 00 | 3 | 66 | 5 | 48 | 6 | 62 | 7 | 15 | 7 | 83 | |
| 4 | 60 | 0 | 17 | 32 | 20 | 00 | 4 | 07 | 6 | 08 | 7 | 36 | 7 | 95 | 8 | 70 |
| 63 | 45 | 20 | 28 | 22 | 61 | 4 | 60 | 6 | 88 | 8 | 32 | 9 | 00 | 9 | 83 | |
| 67 | 30 | 24 | 14 | 26 | 13 | 5 | 31 | 7 | 95 | 9 | 61 | 10 | 39 | 11 | 36 | |
| 71 | 15 | 29 | 46 | 31 | 11 | 6 | 33 | 9 | 47 | 11 | 45 | 12 | 37 | 13 | 53 | |
| 5 | 75 | 0 | 37 | 32 | 38 | 64 | 7 | 86 | 11 | 74 | 14 | 20 | 15 | 36 | 10 | 80 |
| 78 | 45 | 50 | 27 | 51 | 26 | 10 | 43 | 15 | 60 | 18 | 89 | 60 | 38 | 22 | 28 | |
| 82 | 30 | 75 | 96 | 76 | 61 | 15 | 58 | 23 | 32 | 28 | 10 | 30 | 47 | 33 | 31 | |
| 86 | 15 | 152 | 57 | 152 | 90 | 31 | 10 | 46 | 44 | 56 | 26 | 60 | 81 | 66 | 48 | |
| 6 | 90 | 0 | Infin. | Infin. | Infin. | Infin. | Infin. | Infin. | Infin. | |||||||
As in the former Example of the Polar Plane, where BC the height of the Style is found to be 1 Inch 61 cent. if it were required to find the distance between B the top of the Style, and the Points wherein the Hour-lines of 7 in the Morning or 5 in the Afternoon do cross the Equator (which distances I called the Secants of those Hours) either you may extend the Compasses from the Sine of 15 gr. the Complements of the Hour from the Substylar, unto the Sine of 90 gr. so the same extent will reach in the Line of Numbers from 1.61 the length of the Style, unto 6.21, according to the former Canon. Or else you may make use of the following Table, extending the Compasses in the Line of Numbers from 10.00 the length of the Style in the Table, unto 1.61 the length of the Style belonging to your Plane; so the same extent shall reach from 38.64, the Secant in the Table, unto 6.21, and such is your Secant required, the distance between the top of the Style and the point of Intersection, wherein the fifth Hour-line from the Substylar doth cross the Equator.
Again, the same extent will reach from 16.80 the distance in the Table belonging to the fifth Hour-line between the Equator and the Parallel of 13 gr. 30 m. declination, unto 2.70 for the like distance upon your Plane; and so for the rest, which may be gathered, and set down in a Table.
| Hours. | Ang. Po. | Tang. | Secan. | Trop. | |||||
| Gr. | M. | In. | Pa. | In. | Pa. | In. | Pa. | ||
| 12 | 0 | 0 | 0 | 0 | 1 | 61 | 0 | 70 | |
| 11 | 1 | 15 | 0 | 0 | 43 | 1 | 63 | 0 | 72 |
| 10 | 2 | 30 | 0 | 0 | 93 | 1 | 85 | 0 | 80 |
| 9 | 3 | 45 | 0 | 1 | 61 | 2 | 27 | 0 | 99 |
| 8 | 4 | 30 | 0 | 2 | 79 | 3 | 22 | 1 | 40 |
| 7 | 5 | 75 | 0 | 6 | 00 | 6 | 21 | 2 | 70 |
The Tangents and Secants in the third and fourth Columns of this Table are taken out of the Tables of the Natural Tangents and Secants, according to the Degrees and Minutes that are in in the second Column of this Table.
That done, and the Equator drawn as before, if you would draw the Tropicks in the Polar Plane, look into the Table, and take 70 cent. on the first Hour, and 80 on the second Hour, and 2 Inches 70 cent. to the fifth Hour from the Substylar, and the rest of these Distances on their several Hour-lines; and then draw a crooked Line through all these Points, so as it makes no Angles, the Line so drawn shall be the Tropick required. In like manner you may draw any other Parallel of Declination.