The Third Book of the Cross-Staff
CHAP. XIX.
To describe the Vertical Circles in the former Planes.
The Vertical Circles, commonly called Azimuths, are Great Circles drawn through the Zenith, by which we may know in what part of the Heaven the Sun is, how far from the East or West, and how near to the Meridian.
In all upright Planes, whether they be Direct Verticals, or Declining, or Meridian Planes, the Semidiameter of the Horizon will be the same with AB the perpendicular side of the Style, and these Azimuths will be Parallels one to the other, and the distance of each Azimuth from the Foot of the Style upon the Horizontal-line, may be found in this manner.
Consider the length of the Style in Inches and parts of Inches, and the distance of each Azimuth from the Style, according to the Angle at the Zenith in Degrees and Minutes.
- As the Tangent of 45 gr. to the Tangent of Azimuth:
- So the length of the Style, to the length of the Horizontal-line between the Style and the Azimuth.
As if it were required to draw the common Azimuths on the South Face of the Vertical Plane before described, where AB the length of the Style may be supposed to be 10 Inches.
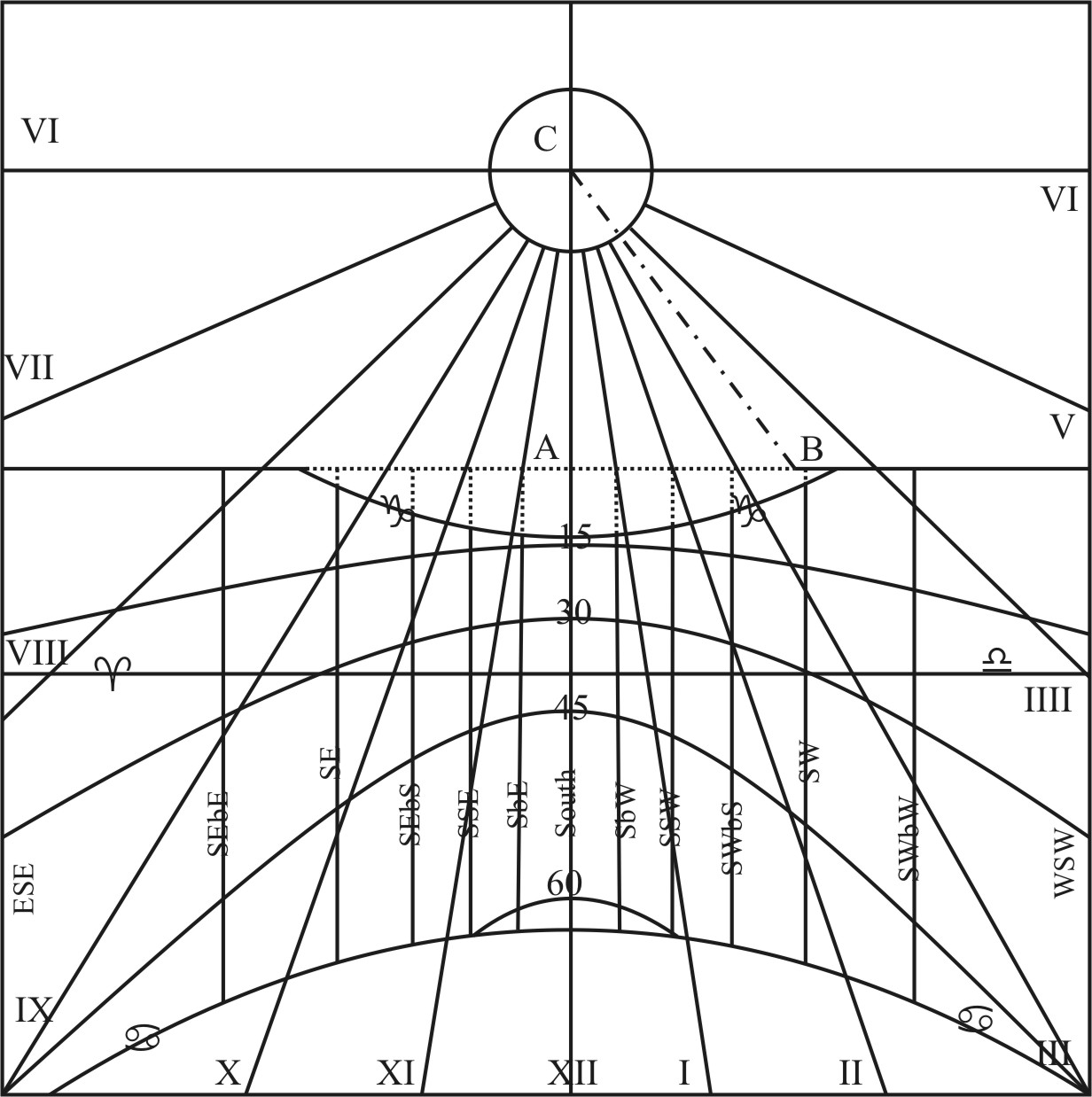
Here the Plane having no declination, the Style is in the Plane of the Meridian, and so pointeth directly to the South. The Point of SbE is 11 gr. 15 m. distant from the Style, and SSE 22 gr. 30 m. and the rest in their order: Wherefore extend the Compasses from the tangent of 45 gr. unto 10 in the Line of Numbers, the same extent will reach from the Tangent of 11 gr. 15 m. unto 1.99 in the Line of Numbers for the length of the Tangent-line, between the Style and the Point SbE; and from the Tangent of 22 gr. 30 m. unto 4.14 for SSE: And so for the rest, as in this Table.
| Azimuths. | An. Zen. | Tang. | ||
| Gr. | M. | In. | Pa. | |
| South | 0 | 0 | 0 | 0 |
| SbE | 11 | 15 | 1 | 99 |
| SSE | 22 | 30 | 4 | 14 |
| SEbS | 33 | 45 | 6 | 68 |
| SE | 45 | 0 | 10 | 00 |
| SEbE | 56 | 15 | 14 | 97 |
| ESE | 67 | 30 | 24 | 14 |
| EbS | 78 | 45 | 50 | 27 |
| East. | 90 | 0 | Infinit. | |
In like manner, in the first Example of the Declining Plane, where the Style standeth according to the Declination 24 gr. 20 m. distant from the South toward the West, the next Point of SbW is but 13 gr. 5 m. distant from the Style; and the second of SSW onely 1 gr. 50 m. and the third of SWbS is again 9 gr. 25 m. and the rest in their order. Wherefore having before found the length of the Style to be 6 Inches 80 parts, extend the Compasses from the Tangent of 45 gr. unto 6.80 parts in the Line of Numbers, the same extent will reach from the Tangent of 24 gr. 20 m. unto 3.07 in the Line of Numbers, for the length of the Tangent-line between the Style and the South; and from the Tangent of 13 gr. 5 m. unto 1.58 for the Point of SbW: and so for the rest, as in this Table.
| Azimuths. | An. Zen. | Tang. | ||
| Gr. | M. | In. | Pa. | |
| SEbE | 80 | 35 | 41 | 00 |
| SE | 69 | 20 | 18 | 03 |
| SEbS | 58 | 5 | 10 | 91 |
| SSE | 46 | 50 | 7 | 25 |
| SbE | 35 | 35 | 4 | 86 |
| South | 24 | 20 | 3 | 07 |
| SbW | 13 | 5 | 1 | 58 |
| SSW | 1 | 50 | 0 | 22 |
| The Foot of the Style | ||||
| SWbS | 9 | 25 | 1 | 13 |
| SW | 20 | 40 | 2 | 57 |
| SWbW | 31 | 55 | 4 | 24 |
| WSW | 43 | 10 | 6 | 37 |
| WbS | 54 | 25 | 9 | 50 |
| West | 65 | 40 | 15 | 02 |
| WbN | 76 | 55 | 19 | 26 |
| WNW | 88 | 10 | 22 | 45 |
That done, if you take these Parts out of a Line of Inches, and prick them down in the Horizontal-line on either side of the Style, drawing Right Lines perpendicular to the Horizon through these Intersections, but so as they may be contained between the Horizontal and the Tropicks, the Lines so drawn shall be the Azimuths required.
In all other Planes inclining to the Horizon, these Vertical Circles will meet in a Point; but that Vertical Point being more or less distant from the Foot of the Style, the Angles at this Point will be unequal.
1. To find the distance between the Foot of the Style and the Vertical Point.
The Vertical Point, wherein all Vertical Lines do meet, will be always in the Meridian, directly under or over the top of the Style; and the Angle between the perpendicular side of the Style, and the Vertical line, will be equal to the Inclination of the Plane to the Horizon. Wherefore,
- As the Tangent of 45 gr. to the Tangent of the Inclination of the Plane:
- So is the length of the Style, to the distance between the Foot of the Style and the Vertical Point.
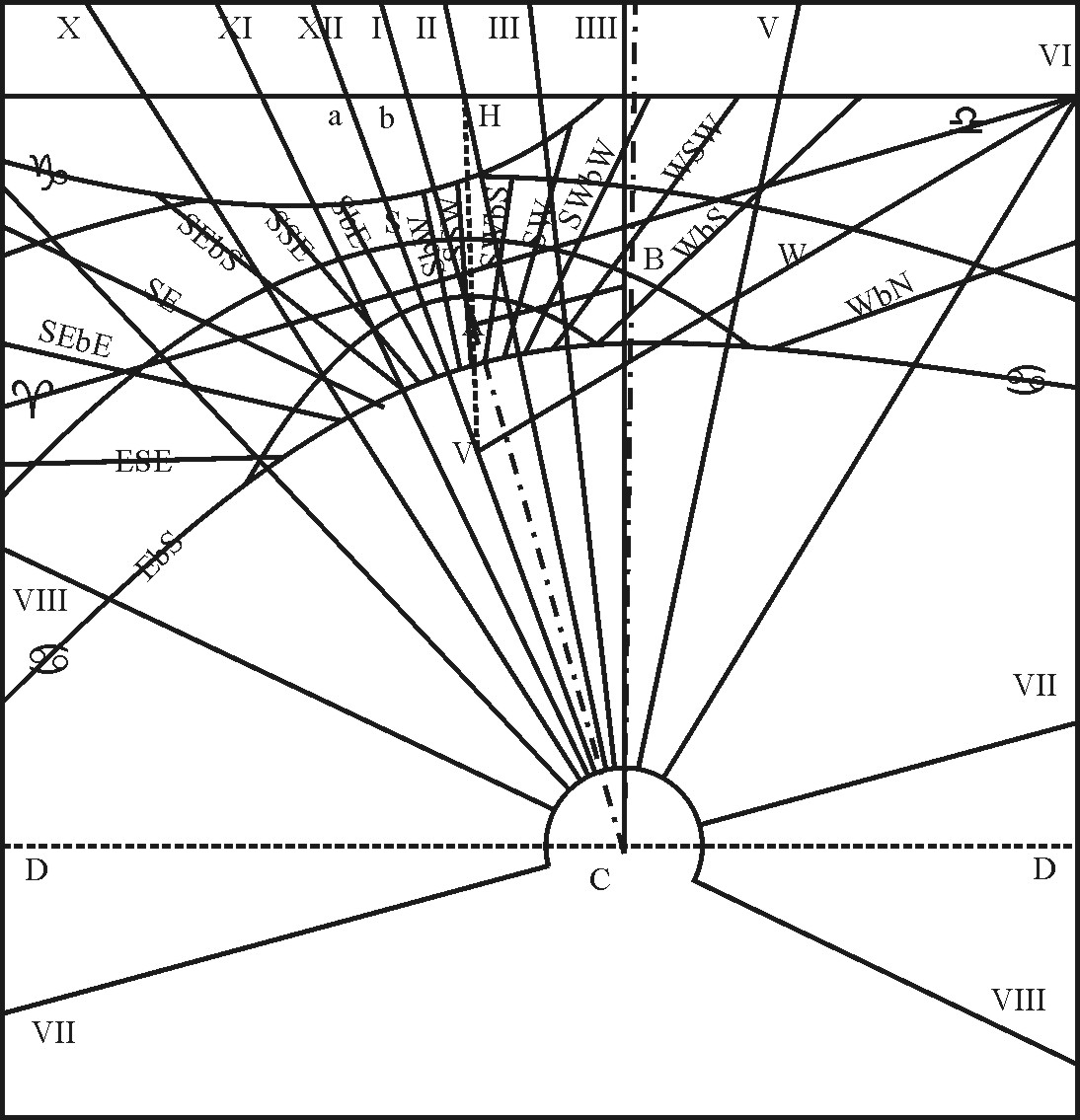
Thus in the first Example of the Declining Inclining Plane, where the upper Face of the Plane looking South-west, the Declination was 24 gr. 20 m. the Inclination 36 gr. and you may suppose AB the length of the Style to be 6 Inches; if you extend the Compasses from the Tangent of 45 gr. unto the Tangent of 36 gr. the same extent will reach in the Line of Numbers from 6.00 unto 4.36, for the distance AV, between A the Foot of the Style and V the Vertical Point.
2. To find the distance between the Foot of the Style and the Horizontal-line.
- As the Tangent of the Inclination of the Plane, is to the Tangent of 45 gr.
- So the length of the Style, to the distance between the Foot of the Style and the Horizontal-line.
So the same extent of the Compasses as before will reach in the Line of Numbers from 6.00 unto 8.26 for the distance AH between the Foot of the Style and the Horizontal-line.
Then may you take 4 inch. 36 cent. and pricking them down from A the Foot of the Style, unto V the Vertical Point in the Meridian, draw the Line VA, which being produced, shall cut the Horizon in the Point H with Right Angles, and be that particular Azimuth which is perpendicular to the Plane.
Or, if you take 8 inch. 26 cent. and prick them down in the former Line VA, produced from A unto H, and so draw the Horizontal-line through H, perpendicular unto VH, which Horizontal-line being produced, will cross the Equator in the same Point wherein the Equator crosseth the Hour-line of 6, unless there be some former error.
3. To find the Angles made by the Azimuth-lines at the Vertical Point.
The Angles at the Zenith depend on the Declination of the Plane, as in our Example, where the Style standeth according to the Declination 14 gr. 20 m. distant from the South toward the West, the Azimuth of 10 gr. from the Meridian Eastward will be 24 gr. 20 m. the Azimuth of 10 gr. Westward will be onely 14 gr. 20 m. distant from the Style; and so the rest in their order.
Or if you would rather describe the common Azimuths, the Point of SbE will be 35 gr. 35 m. the Point of SbW 13 gr. 5 m. distant from the Style; and so the rest in their order. Then,
- As the Sine of 90 gr. to the Co-sine of the Inclination of the Plane:
- So the Tangent of the Angle at the Zenith, to the tangent of the Angle at the vertical Point, between the Line drawn through the Foot of the Style, and the Azimuth required.
Wherefore the Inclination of the Plane in our Example being 36 gr. extend the Compasses from the Sine of 90 gr. unto the Sine of 54 gr. the same extent shall reach in the Line of Tangents from 24 gr. 20 m. unto 20 gr. 5 m. for the Angle HVa at the Vertical Point, between the Line VH, drawn through A the Foot of the Style, and the South. Again the same extent will reach from the Tangent of 13 gr. 5 m. unto 10 gr. 38 m. for the Angle belonging to SbW; and so the rest, as in this Table.
| Azimuths. | An. Zen. | Ang. V. | ||
| Gr. | M. | Gr. | M. | |
| SEbE | 80 | 35 | 78 | 25 |
| SE | 69 | 20 | 65 | 0 |
| SEbS | 58 | 5 | 52 | 25 |
| SSE | 46 | 50 | 40 | 40 |
| SbE | 35 | 35 | 30 | 3 |
| South | 24 | 20 | 20 | 5 |
| SbW | 13 | 5 | 10 | 39 |
| SSW | 1 | 50 | 1 | 29 |
| Style. | 0 | 20 | ||
| SWbS | 9 | 25 | 7 | 38 |
| SW | 20 | 40 | 16 | 58 |
| SWbW | 31 | 55 | 26 | 45 |
| WSW | 43 | 10 | 37 | 11 |
| WbS | 54 | 25 | 48 | 30 |
| West | 65 | 40 | 60 | 48 |
| WbN | 76 | 55 | 73 | 58 |
| WNW | 88 | 10 | 87 | 42 |
These Angles being known, if on the Center V, at the Vertical Point, you describe an occult Circle, and therein inscribe the Chords of these Angles from the Line VH, and then draw Right Lines through the Vertical Point, and the Terms of those Chords, the Lines so drawn shall be the Azimuths required. The like reason holdeth for drawing of the Azimuths upon all other Inclining Planes, whereof you have another Example in the Diagram belonging to the Meridian Incliner, as before.
Or, for further satisfaction, you may find where each Azimuth-line shall cross the Equator.
- As the Sine of 90 gr. to the Sine of the Latitude:
- So the Tangent of the Azimuth from the meridian, to the tangent of the Equator from the Meridian.
Extend the Compasses from the Sine of 90 gr. unto the Sine of our Latitude 51 gr. 30 m. the same Extent will reach in the Line of Tangents from 10 gr. unto 7 gr. 50 m. for the Intersection of the Equator with the Azimuth of 10 gr. from the Meridian,. Again the same extent will reach from 20 gr. unto 15 gr. 54 m. for the Azimuth of 20 gr. And so the rest, as in this Table.
| Azim. | Equat. | Azim. | Equat. | |||||
| Gr. | M. | Gr. | M. | Gr. | M. | Gr. | M. | |
| 10 | 0 | 7 | 50 | 11 | 15 | 0 | 51 | |
| 20 | 0 | 15 | 54 | 22 | 30 | 19 | 58 | |
| 30 | 0 | 24 | 20 | 33 | 45 | 27 | 36 | |
| 40 | 0 | 33 | 18 | 45 | 0 | 38 | 2 | |
| 50 | 0 | 43 | 0 | 56 | 15 | 49 | 30 | |
| 60 | 0 | 53 | 35 | 67 | 30 | 62 | 6 | |
| 70 | 0 | 65 | 3 | 78 | 45 | 75 | 44 | |
| 80 | 0 | 77 | 18 | 90 | 0 | 90 | 0 | |
| 90 | 0 | 90 | 0 | |||||
By which you may see that the Azimuth 90 gr. distant from the Meridian, which is the Line of East and West, will cross the Equator at 90 gr. from the Meridian, in the same Point with the Horizontal-line and the Hour of 6 and that the Azimuth of 45 gr. will cross the Equator at 38 gr. 2 m. from the Meridian; that is, the Line of SE will cross the Equator at the Hour of 9 and 28 m. in the Morning, and the Line SW at 2 ho. 31 m. in the Afternoon: And so the rest, whereby you may examine your former Work.