The Third Book of the Cross-Staff
CHAP. XX.
To describe the Parallels of the Horizon in the former Planes.
The Parallels of the Horizon, commonly called Almicanters, or Parallels of Altitude (whereby we may know the Altitude of the Sun above the Horizon) have such respect unto the Horizon, as the Parallels of Declination unto the Equator, and so may be described in like manner.
In an Horizontal Plane these Parallel will be perfect Circles; wherefore knowing the length of the Style in Inches and parts, and the distance of the Parallels from the Horizon in Degrees and Minutes,
- As the Tangent of 45 gr. is to the length of the Style:
- So is the Co-tangent of the Parallel, to the Semidiameter of his Circle.
Thus in the Example of the Horizontal Plane, if AB the length of the Style shall be 5 Inches, and that it were required to find the Semidiameter of the Parallel of 62 gr. extend the Compasses from the tangent of 45 gr. unto 5.00 in the Line of Numbers, the same extent will reach from the Tangent of 28 gr. the Complement of the Parallel, unto 2.65: And if you describe a Circle on the Center A, to the Semidiameter of 2 inch. 65 cent. it shall be the Parallel required.
In all upright Planes, whether they be Direct Verticals, or Declining, or Meridian Planes, these parallels will be Conical Sections, and may be drawn through their Points of Intersection with the Azimuth-lines, in the same manner as the Parallels of Declination through their Points of Intersection with the Hour-lines. To this end, you may first find the distance between the top of the Style and the Azimuth, and then the distance between the Horizon and the Parallel, both which may be represented in this manner.
On the Center B, and any Semidiameter BH, describe an occult Ark of a Circle, and therein inscribe the Chords of such parallel of Altitude as you intend to draw on the Plane, (I have here put them for 15, 30, 45, and 60 gr.) then draw Right Lines through the Center and the Terms of these Chords, so the Line BH shall be the Horizon, and the rest the Lines of Altitude, according to their distance from the Horizon.
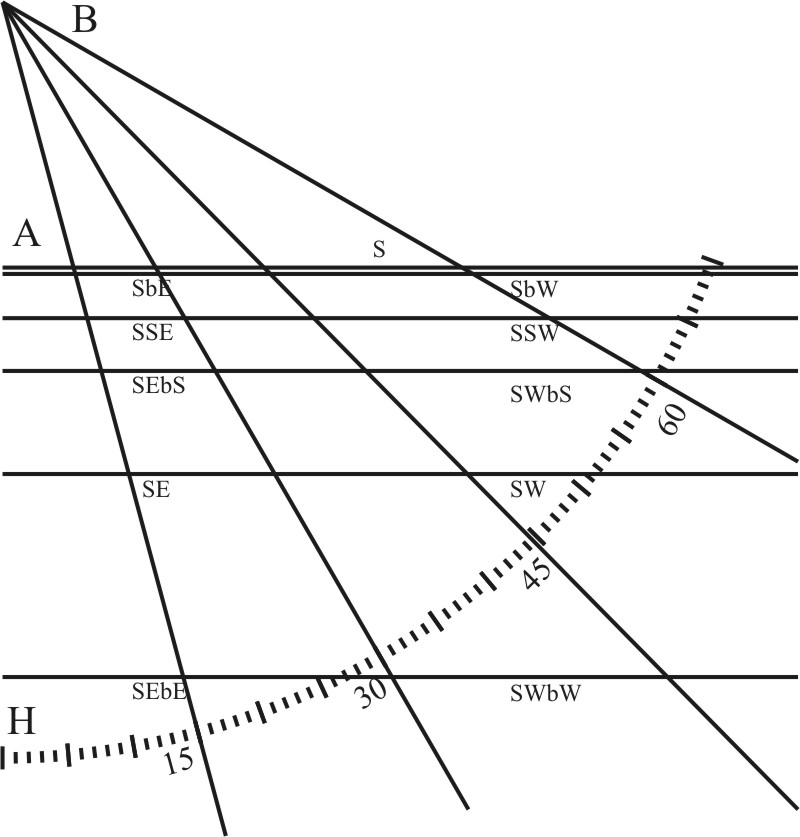
That done, consider your Plane, (which here for example is the South Face of our Vertical Plane) wherein having drawn both the Horizontal and Vertical Lines, as I shewed before, first take out AB the length of the Style, and prick that down in this Horizontal Line from B unto A; then take out all distances between B and the top of the Style and the several Points wherein the Vertical Lines do cross the Horizontal, transfer them into this Horizontal-line BH, from the Center B, and the Terms of these distances erect Lines perpendicular to the Horizon, noting them with the Number of Letter of the Azimuth from whence they are taken; so these Perpendiculars shall represent those Azimuths, and the second distance between the Horizon and the Lines of Altitude shall give the like distance between the Horizontal and the parallels of Altitude upon the Azimuths in your Place. Upon this ground it followeth,
1. To find the distance between the top of the Style, and the several Points wherein the Azimuths do cross the Horizontal-line.
Having drawn the Horizontal and Azimuth Lines as before, look into the Table by which you drew them, and there you shall have the Angles at the zenith. Then,
- As the Co-sine of the Angle at the Zenith, is to the Sine of 90 gr.
- So the length of the Style, to the Distance required.
| Azimuths. | Ang. Ze. | Tangent | Secant. | Par. 15. | Par. 30. | |||||
| Gr. | M. | In. | Pa. | In. | Pa. | In. | Pa. | In. | Pa. | |
| South | 0 | 0 | 0 | 0 | 10 | 00 | 2 | 68 | 5 | 77 |
| SbE | 11 | 15 | 1 | 99 | 10 | 20 | 2 | 73 | 5 | 90 |
| SSE | 22 | 30 | 4 | 14 | 10 | 82 | 2 | 90 | 6 | 14 |
| SEbS | 33 | 45 | 6 | 68 | 12 | 03 | 3 | 23 | 6 | 94 |
| SE | 45 | 0 | 10 | 00 | 14 | 14 | 3 | 80 | 8 | 16 |
| SEbE | 56 | 15 | 14 | 97 | 18 | 00 | 4 | 82 | 10 | 40 |
| ESE | 67 | 30 | 24 | 14 | 26 | 13 | 7 | 02 | 15 | 08 |
| EbS | 78 | 45 | 50 | 27 | 51 | 26 | 13 | 73 | 29 | 60 |
| East. | 90 | 0 | Infinit. | Infinit. | Infinit. | Infinit. | ||||
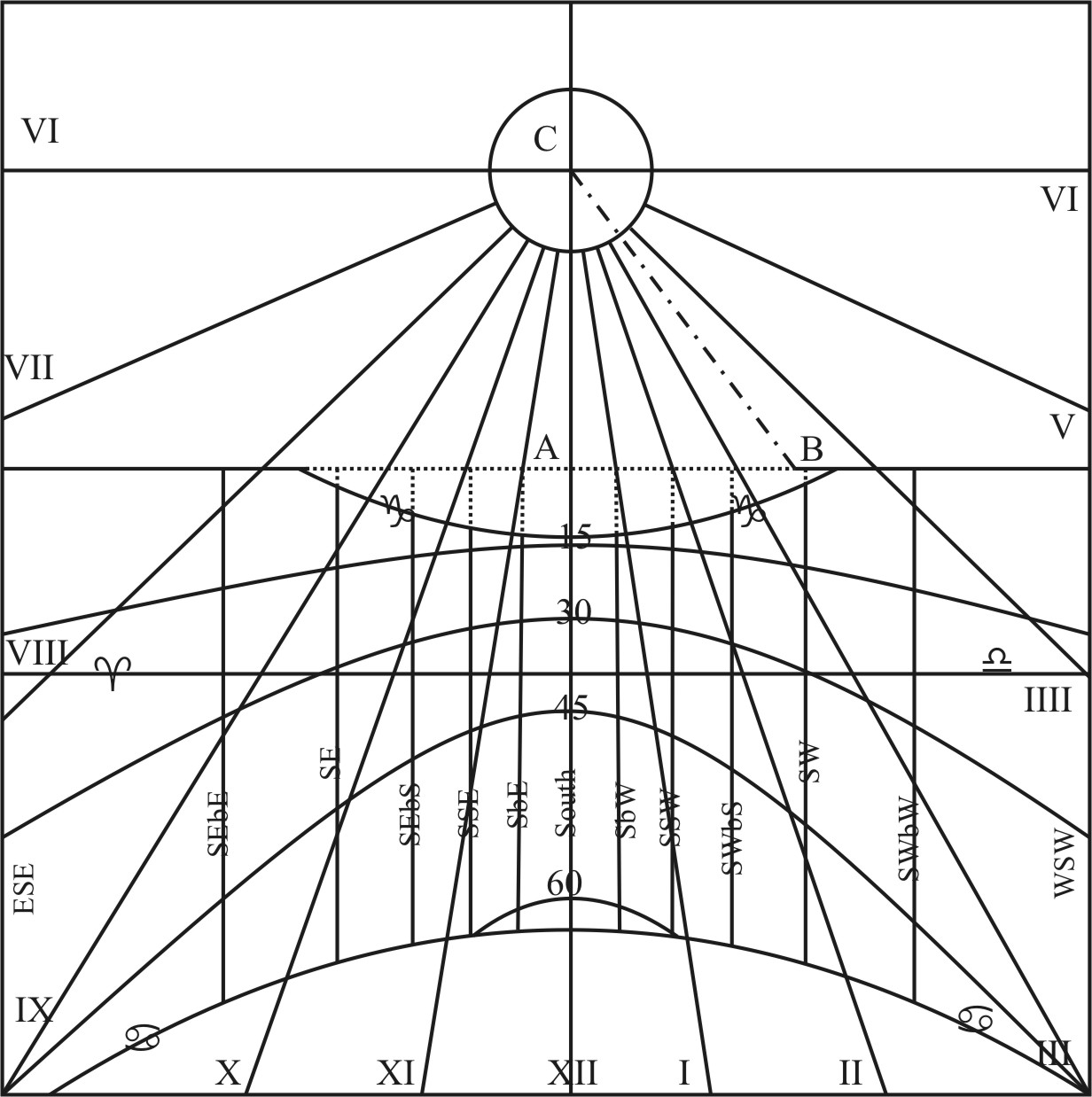
As in our Example of the Vertical Plane, where AB the length of the Style was supposed to be 10 Inches, extend the Compasses from the Sine of 78 gr. 45 m. (the Complement of 11 gr. 15 m. the Angle at the zenith, belonging to SbE and SbW) unto the Sine of 90 gr. the same extent will reach from 10.00 the length of the Style, unto 10.20, for the distance between the top of the Style and the Intersection of the Azimuth SbE with the Horizontal line, which distance may be called the Secant of the Azimuth, and may serve for the drawing of the Parallel of 45 gr. from the Horizon. The like reason holdeth for the rest of these distances here represented in the Line BH.
2. To find the distance between the Horizon and the Parallels.
- As the Tangent of 45 gr. to the Tangent of the Parallel:
- So the Secant of the Azimuth, to the Distance required.
As if it were required to draw the Parallel of 15 gr. from the Horizon, upon this Vertical Plane; extend the Compasses from the Tangent of 45 gr. unto the Tangent of 15 gr. the same extent will reach in the Line of Numbers from 10.00 the Secant of the South Azimuth, unto 2.68, and therefore the distance between the Horizon and the Parallel of 15 gr. is 1 inch. 68 cent. unto the South Azimuth. Again, the same extent will reach from 10.20 the Secant of SbE, unto 2.73, for the like distance belonging to SbE and SbW: And so for the rest, which may be gathered and set down in the Table.
That done, and the Horizon and Azimuths being drawn, prick down 10 Inches from the Horizontal-line upon the South Azimuths of SbE and SbW, and 10 inch. 82 cent. on the Azimuths of SEbS and SWbS, and so the rest of these distances on their several Azimuths: then if you draw a crooked Line through these Points, that may make no Angles, the Line so drawn shall be the Parallel of 45 gr. from the Horizon. In like manner may you draw the parallel of 15 gr. or nay other Parallel of Altitude, upon any Vertical Plane.
If the Plane incline to the Horizon, after we have found the Vertical Point, and drawn the Horizontal-line, we are farther to find the length of the Axis of the Horizon, then the Angles betwixt this Axis and the Azimuth-lines, and so the several distances between the parallel and the Vertical Point, all which may be represented in this manner.
On the Center B, and any Semidiameter, describe an occult Quadrant of the Circle, and therein inscribe the Chords of such Parallels of Altitude as you iuntend to draw on the Plane, drawing Right Lines through the Center and the Terms of these Chords, so the Line BH shall be the Horizon, and his Perpendicular BV the Axis of the Horizon, and the rest the Lines of Altitude, according to their distance from the Horizon.
That done, consider your Plane, which here, for example, is the first of our three Declining Inclining Planes; wherein having drawn both the Horizontal and vertical Lines, as I shewed before, first take out the Axis of the Horizon, which is the Line between B the top of the Style and V the Vertical Point, and prick that down in this Figure from B unto V; then take out both the Line VH, and all the rest of the distances between V the Vertical Point and the several Points wherein the Vertical Lines do cross the Horizontal Line of this Figure from the Point V, noting the place where they cross the Horizontal-line, with the Number or Letter of the Azimuth from whence they were taken, and drawing the Azimuth-lines from V through the Lines of the Altitude.
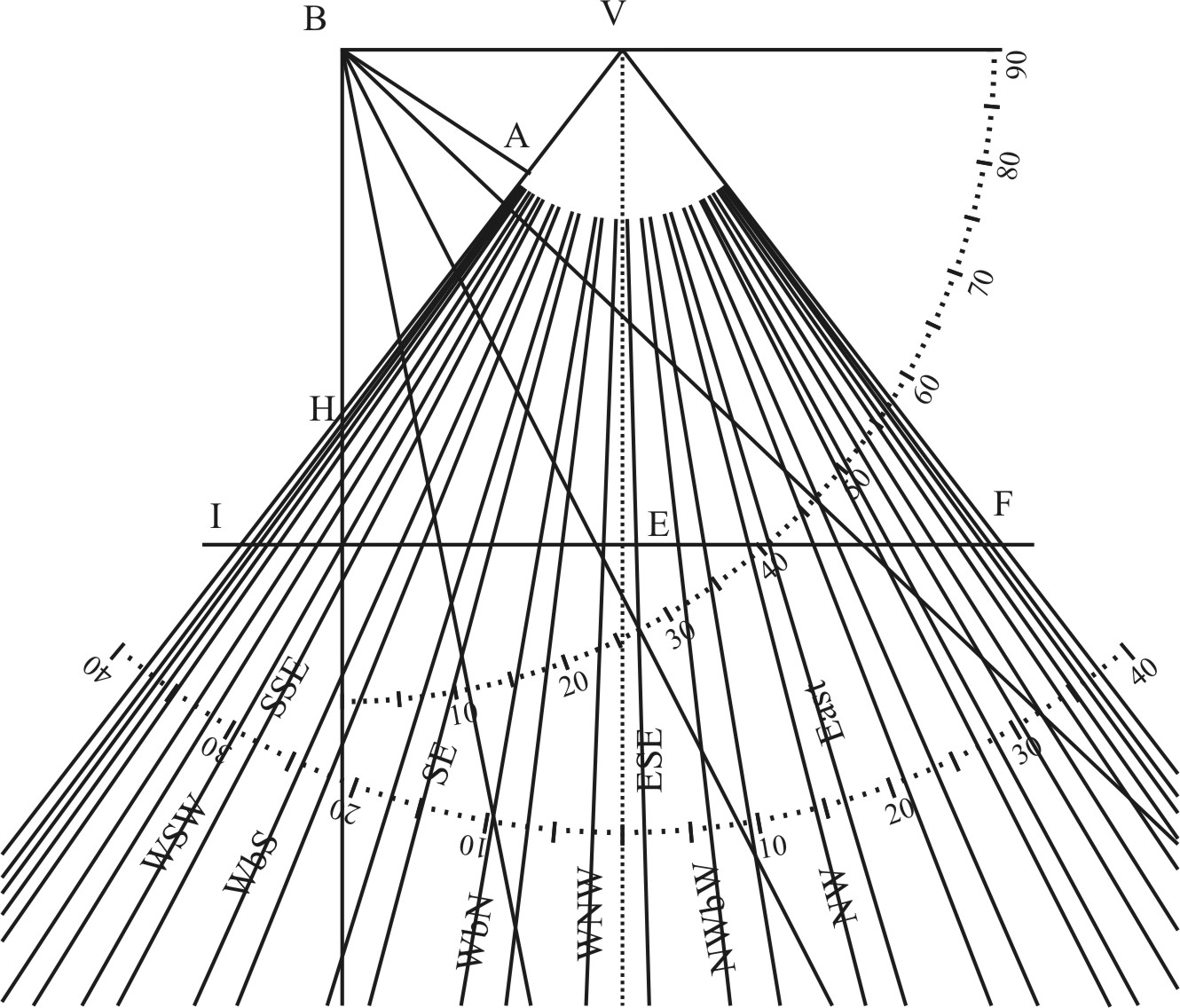
Or having the Sector, you may draw an occult Line VE, perpendicular to the Axis VB, and therein prick down the Tangent of the Complement of the Inclination of the Plane from V unto E: then draw the Line EF parallel to the Axis, crossing the Line VH produced in the Point F; so this Line EF will be as the Line of Sines upon the Sector, and therein you may prick down the Sines of the Complement of the Angles at the Zenith from E towards F, and draw the Vertical-lines by those Points through the Lines of Altitude; so the Angles at V, between the Axis VB and those Azimuth-lines, shall be the Angles between the Axis of the Horizon and the Azimuth-lines on your Plane, and the several distances between the Point V and the Lines of Altitude shall give the like distances between the Vertical Point and the Parallel of Altitude upon the Azimuths in your Plane. Upon this ground followeth,
1. To find the length of the Axis of the Horizon.
The Vertical Point is always either directly over or under the top of the Style, and the distance between them is that which I call the Axis of the Horizon, which may thus be found:
- As the Co-sine of the Inclination, to the Sine of 90 gr.
- So the length of the Style, to the length of the Axis of the Horizon.
For example, in the first of the three declining Inclining Planes, the Inclination to the Horizon is 36 gr. the length of the Style AB 6 Inches; extend the Compasses from the Sine of 54 gr. the Complement of the Inclination, unto the Sine of 90 gr. the same extent will reach in the Line of Numbers from 6.00 unto 7.42; and such is VB the length of the Axis required.
2. To find the Angles contained between the Horizon and the Vertical Lines upon your Plane.
The Angles at the Vertical Point between the Axis of the Horizon and the Azimuth-lines upon your Plane are represented in this Figure by those at V, between VB and the Azimuths. The Angles between the Horizon and the Azimuth-lines being Complements to the former, are represented either by those which are made by VE, or by BH, and the Azimuth-lines which are drawn from V.
That you may find them, look into the Table by which you drew the Azimuth-lines, there shall you find the Angles at the Zenith, Then,
- As the Sine of 90 gr. to the Co-sine of the Angle at the Zenith:
- So the Tangent of the Inclination to the Horizon, to the Tangent of the Angle between the Horizon and the vertical Line.
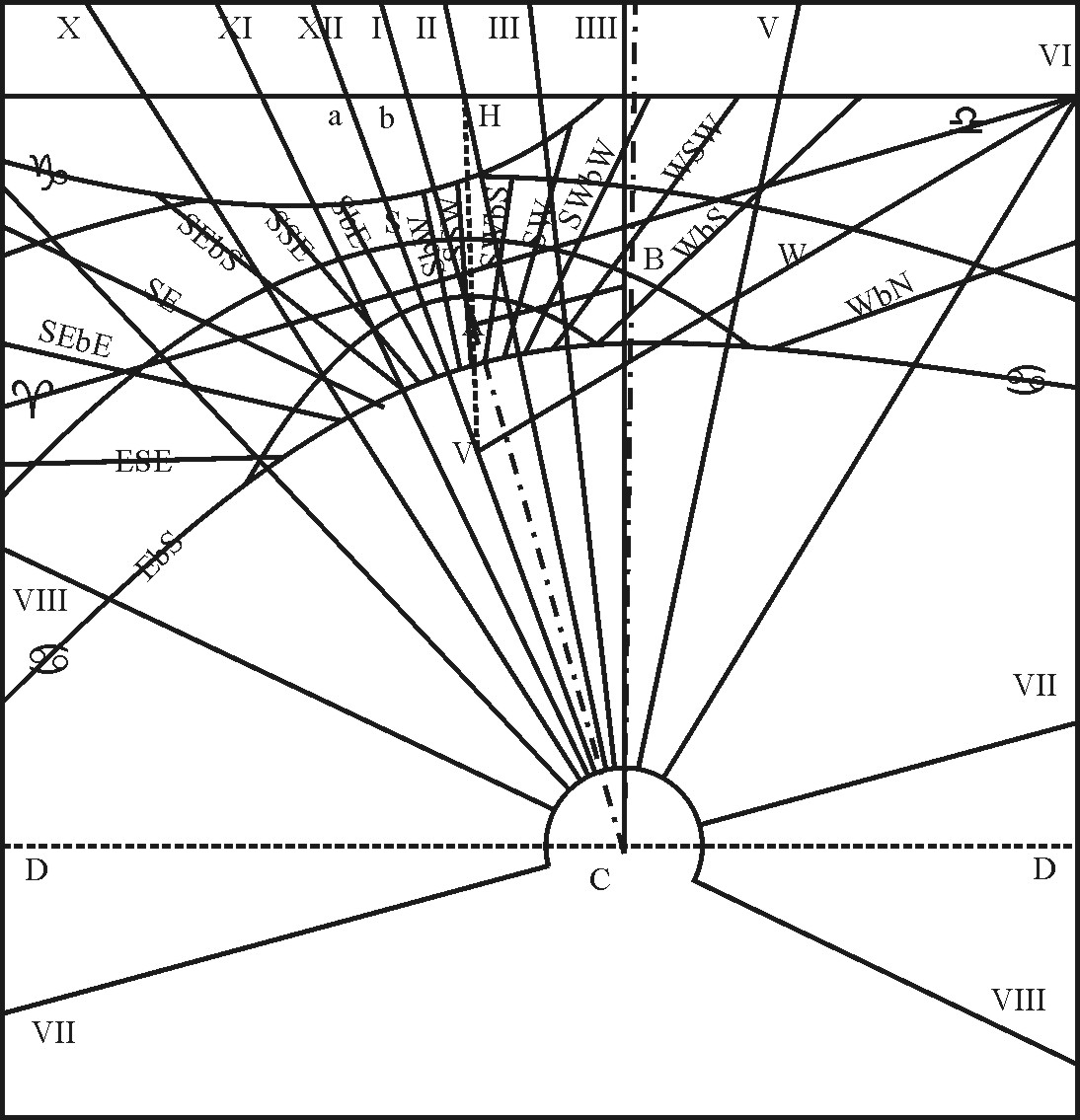
In our example, where the Inclination to the Horizon is 36 gr. and the Angle at the Zenith, between the Azimuth at the Style and the Meridian, is according to the Declination 24 gr. 30 m. extend the Compasses from the Sine of 90 gr. unto the Tangent of 30 gr. the same extent will reach from the Sine of 65 gr. 40 m. the Complement of the Angle at the zenith, unto the Tangent of 33 gr. 30 m. for the Angle contained between the Horizon and the South part of the Meridian-line. Again, the same extent will reach from the Co-sine of 35 gr. 35 m. the Angle at the Zenith belonging to SbE, unto the Tangent of 30 gr. 3 m. for the Angle between the Horizon and the Azimuth-line of SbE. The like reason holdeth for the rest, which may be found and set down in a Table.
| Azimuths. | Ang. Ze. | Ang. V. | An. Ho. | Horiz. | 11 | 18 | 26 | 34 | 45 | 0 | ||||
| Gr. | M. | Gr. | M. | Gr. | M. | In. | Pa. | In. | Pa. | In. | Pa. | In. | Pa. | |
| East. | 114 | 20 | 119 | 12 | 16 | 40 | Infinite. | 38 | 60 | 11 | 05 | |||
| EbS | 103 | 5 | 106 | 2 | 9 | 20 | 210 | 24 | 22 | 40 | 9 | 00 | ||
| ESE | 91 | 50 | 92 | 16 | 1 | 20 | 41 | 98 | 15 | 57 | 7 | 60 | ||
| SEbE | 80 | 35 | 78 | 25 | 6 | 47 | 62 | 82 | 23 | 44 | 12 | 07 | 6 | 68 |
| SE | 69 | 20 | 65 | 0 | 14 | 23 | 29 | 87 | 16 | 79 | 10 | 12 | 6 | 00 |
| SEbS | 58 | 5 | 52 | 25 | 21 | 0 | 20 | 70 | 13 | 61 | 8 | 99 | 5 | 79 |
| SSE | 46 | 50 | 40 | 46 | 26 | 25 | 16 | 68 | 11 | 90 | 8 | 31 | 5 | 53 |
| SbE | 35 | 35 | 30 | 3 | 30 | 35 | 14 | 58 | 10 | 90 | 7 | 90 | 5 | 42 |
| South | 24 | 20 | 20 | 5 | 33 | 30 | 13 | 44 | 10 | 32 | 7 | 66 | 5 | 35 |
| SbW | 13 | 5 | 10 | 39 | 35 | 17 | 12 | 84 | 10 | 02 | 7 | 55 | 5 | 33 |
| SSW | 1 | 50 | 1 | 29 | 35 | 59 | 12 | 62 | 9 | 90 | 7 | 47 | 5 | 31 |
| Style | 0 | 0 | 36 | 0 | 12 | 62 | 9 | 90 | 7 | 47 | 5 | 31 | ||
| SWbS | 9 | 25 | 7 | 38 | 35 | 37 | 12 | 74 | 9 | 90 | 7 | 50 | 5 | 32 |
| SW | 20 | 40 | 16 | 58 | 34 | 12 | 13 | 20 | 10 | 20 | 7 | 59 | 5 | 34 |
| SWbW | 31 | 55 | 26 | 45 | 31 | 46 | 14 | 13 | 10 | 67 | 7 | 81 | 5 | 39 |
| WSW | 43 | 10 | 37 | 11 | 27 | 55 | 15 | 85 | 11 | 50 | 8 | 15 | 5 | 49 |
| WbS | 54 | 25 | 48 | 30 | 22 | 55 | 19 | 05 | 12 | 94 | 8 | 73 | 5 | 66 |
| West | 65 | 40 | 60 | 48 | 16 | 40 | 25 | 87 | 15 | 51 | 9 | 60 | 5 | 96 |
| WbN | 76 | 55 | 73 | 58 | 9 | 20 | 45 | 75 | 20 | 64 | 11 | 32 | 6 | 46 |
| WNW | 88 | 10 | 87 | 44 | 1 | 20 | 318 | 88 | 33 | 27 | 14 | 18 | 7 | 25 |
| NWbW | 99 | 25 | 101 | 35 | 6 | 47 | Infinite | 92 | 40 | 19 | 60 | 8 | 48 | |
| NW | 10 | 40 | 115 | 00 | 14 | 23 | 31 | 44 | 10 | 30 | ||||
Then may you either draw these Angles at V in the former Figure more perfectly, and thence finish your Work, or else proceed.
3. To find the distance between the Vertical Point, and the parallel of the Horizon.
These distances may be found by resolving the Triangles in the last Figure made by the Axis, the Lines of Altitude, and the Azimuth-lines. For having the length of the Axis, and the Angle at the Horizon, if you add the distance of the parallel from the Horizon, unto the Angle at the Horizon, you shall have the Angle at the Parallel. Then,
- As the Sine of the Angle at the Parallel, to the Co-sine of the Altitude:
- So the length of the Axis, to the distance between the Vertical Point and the Parallel.
Thus in our Example, if it were required to find the distance upon the Stylar Azimuth VH, between the Vertical Point and the Horizon, you have the Rectangle Triangle VBH, wherein the Angle at the Horizon here represented by BHV is (equal to the Inclination of the Plane) 36 gr. and BV the Axis of the Horizon between the Plane and the top of the Style is 7 inch. 42 cent. Wherefore extend the Compasses from the Sine of 36 gr. unto the Sine of 90 gr. the Complement of the Altitude, the same extent will reach in the Line of Numbers from 7.42 unto 12.62; and such is the distance of the Perpendicular Azimuth-line VH, between the Vertical Point and the Horizon.
In like manner, if you would find the distance upon the Meridian between the Vertical Point and the Horizon, extend the Compasses from the Sine of 33 gr. 30 m. the Angle at the Horizon, to the Sine of 90 gr. the same extent will reach in the Line of Numbers from 7.42 unto 13.44, and such is Va the distance between the Vertical Point and the Horizon upon the Line of the South Azimuth, that is, upon the Meridian-line.
But if you would find the distance upon the Meridian between the Vertical Point and any other Parallel of the Horizon, as upon the Parallel of 26 gr. 34 m. then add these 26 gr. 34 m. unto 33 gr. 30 m. the Angle at the Horizon, so shall you have 60 gr. 4 m. for BDV the Angle at the Parallel. And if you extend the Compasses from the Sine of 60 gr. 4 m. unto the Sine of 63 gr. 26 m. the Complement of the Parallel from the Horizon, the same extent will reach in the Line of Numbers from 7.42 the length of the Axis, unto 7.66, and such is the distance VD between the Vertical Point and the Parallel of 26 gr. 34 m. upon the Meridian-line. The like reason holdeth for all the rest, which may be gathered and set down in a Table.
That done, and the Horizon drawn as before, if you would draw the Parallel of 26 gr. 34 m. from the Horizon, look into the Table, and there finding under the Title of the Parallel of 26.34 the distance on the South Azimuth-line to be 7.66, take 7 inch. 66 cent. out of a Line of Inches, and prick them down on the Meridian of your Plane from the Vertical Point at V.
Or if either the Vertical Point fall without your Plane, or the extent at any time be too large for your Compasses, you may prick down the distance between the Horizon and the Parallel. As here the distance between the Vertical Point and the Parallel is 7.66, between the Vertical Point and the Horizon 13.44, the difference between them 5.78 is the distance from the Horizon to the Parallel, which being pricked down upon the Meridian, shall give the same Intersection as before. And the like reason holdeth for the pricking down the rest of their distances on their several Azimuths.
Having the Point of Intersection between the Azimuths and the Parallel, you may joyn them all in a crooked Line, without making of Angles; the Line so drawn shall be the Parallel required. And upon this ground it followeth,
To describe such Parallels on the former Planes, as may shew the proportion of the Shadow unto the Gnomon.
The proportion of a Mans Shadow unto his Height, or other Shadow to his Gnomon, set perpendicular to the Horizon, may be shewed by Parallels to the Horizon, if they be drawn to a due Altitude, which may thus be found:
- As the length of the Shadow, to the lengths of the Gnomon:
- So the Tangent of 45 gr. to the Tangent of the Altitude.
As if it were required to find the Altitude of the Sun when the Shadow of a Man shall be decuple to his height, extend the Compasses from 10 unto 1 in the Line of Numbers, the same extent will reach in the Tangent of 45 gr. unto the tangent of 5 gr. 42 m. which shews that when the Sun cometh to the Altitude of 5 gr. 42 m. your Shadow upon a level Ground will be ten times as much as your Height. In the same manner you may find, that at 7 gr. 7 m. of Altitude your Shadow will be a duple, at 9 gr. 27 m. sextuple, at 11 gr. 18 m. quintuple, at 14 gr. 2 m. quadruple, at 18 gr. 26 m. triple, at 26 gr. 33 m. double to your Height, at 33 gr. 41 m. as 3 unto 2, at 36 gr. 52 m. as 2 unto 3, at 34 gr. 39 m. as 5 unto 4, at 45 gr. equal, at 51 gr. 20 m. as 4 unto 5, at 53 gr. 7 m. as 3 unto 4, at 56 gr. 19 m. as 4 unto 3, at 58 gr. 2 m. as 3 unto 5, at 63 gr. 26 m. as 1 unto 2, &c.
If then you draw a parallel to the Horizon at 5 gr. 42 m. another at 7 gr. 7 m. and so the rest, when the shadow iof the Style falleth on the parallel, you have the proportion, and thereby may you know the Shadow by the Height, and the height by the Shadow, whereof you have an example pag. 8.
I might here proceed to shew the Description of the Circles of Position, the Signs of the Zodiack in the Meridian, the Signs ascending and descending, with such other Gnomonical Conclusions: but these would prove superfluous to such as understand the Doctrine of the Shere; and for others, that which is delivered may suffice for ordinary use, it being my intention not so much to explain the full use of Shadows, (whereof I have lately given a large example in another place) as the use of these Lines of Proportion, that were not extant heretofore.