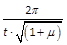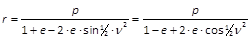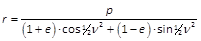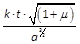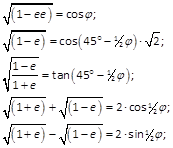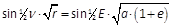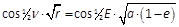Gauss und die Bewegung der Himmelskörper

Carl Friedrich Gauss (1777 - 1855) veröffentlichte 1809 seine Theoria Motus Corporum Coelestium, dessen deutsche Übersetzung von Carl Haase aus dem Jahr 1865 mir vorliegt.

Carl Friedrich Gauss leitet die Kepler-Gleichung aus den Gesetzen von Isaac Newton ab, und verwendet die Differentialrechnung zur Beschreibung der Kegelschnitte:

Erstes Buch.
Allgemeine Relationen unter den Grössen, durch welche die Bewegungen der Himmelskörper um die Sonne bestimmt werden.
Erster Abschnitt.
Relationen, die einen einzelnen Ort in der Bahn betreffen.

1.

Wir wollen die Bewegungen der Himmelskörper in diesem Werke nur insoweit betrachten, als solche von der Anziehungskraft der Sonne abhängig sind. Ausgeschlossen bleiben daher hier alle secundären Planeten, ingleichen die Störungen, welche die Primären wechselseitig auf sich ausüben, sowie auch alle rotatorisehen Bewegungen. Die bewegten Körper selbst wollen wir als mathematische Punkte betrachten und voraussetzen, dass alle Bewegungen nach Massgabe der nachfolgenden Gesetze vor sich gehen, welche daher als die Grundlage aller Untersuchungen im gegenwärtigen Werke anzusehen sind.

  1. Die Bewegung eines jeden Himmelskörpers geschieht beständig in der nämlichen Ebene, in welcher zugleich der Mittelpunkt der Sonne liegt.
  2. Der von dem Körper beschriebene Linienzug ist ein Kegelschnitt, der seinen Brennpunkt im Mittelpunkte der Sonne hat.
  3. Die Bewegung in jenem Linienzuge geht in der Weise vor sich, dass die in verschiedenen Zeitabschnitten um die Sonne beschriebenen Flächenräume diesen Zeitabschnitten proportional sind. Drückt man daher Zeiten und Flächenräume durch Zahlen aus, so ergiebt jeder Flächenraum, wenn man ihn durch die Zeit, innerhalb deren er beschrieben wurde, dividirt, einen unveränderlichen Quotienten.
  4. Für die verschiedenen, um die Sonne sich bewegenden Körper stehen die Quadrate dieser Quotienten im zusammengesetzten Verhältnisse der den Bahnen entsprechenden Parameter und der Summen der Sonnenmasse und der Massen der bewegten Körper.

Bezeichnet also 2p den Parameter der Bahn, in welcher der Körper einherzieht; μ die Stoffmenge dieses Körpers (die Masse Sonne = 1 gesetzt); ½g die Fläche, welche der Körper in der Zeit t um die Sonne beschreibt; so wird 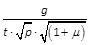Formel eine Constante für alle Himmelskörper bilden.

Da es also gleichgültig ist, welchen Himmelskörper man zur Bestimmung dieser constanten Zahl benutzt, so wollen wir letztere aus der Bewegung der Erde ableiten, und dabei deren mittlere Entfernung von der Sonne zur Distanz-Einheit annehmen. Die Einheit der Zeit soll stets der mittlere Sonnentag sein. Bezeichnet man ferner mit π das Verhältniss der Peripherie zum Durchmesser des Kreises, so wird der Flächenraum der ganzen, von der Erde beschriebenen Ellipse offenbar sein = π√p, welcher daher = ½g zu setzen ist, wenn man für t das siderische Jahr annimmt, wodurch unsere Constante

  • Formel

wird. Um den numerischen Werth dieser Constante, die wir im Folgenden mit k bezeichnen wollen, zu ermitteln, setzen wir nach der neuesten Bestimmung das siderische Jahr, oder t = 365,2563835, die Masse der Erde oder μ = 1/354710 = 0,0000028192; dadurch wird erhalten:

log 2·π 0,798 179 8684
compl. log t 7,437 402 1852
compl. log √(1+μ) 9,999 999 3878
log k 8,235 581 4414
k = 0,0172 020 9895.

Anmerkung: der "Parameter der Bahn p" ist definiert als Länge der Ellipsen-Halbsehne parallel zur kleinen Achse und senkrecht auf der großen im Brennpunkt der Ellipse. Gauss zitiert im Vorwort Isaac Newton: "dass endlich die von verschiedenen Körpern in gleichen Zeiten um die Sonne beschriebenen Flächen sich wie die Quadratwurzeln der Halbparameter der Bahnen verhalten." [Berechnung separat]

2.

Die so eben erörterten Gesetze, weichen von den durch Kepler entdeckten nur in der Weise ab, dass sie in einer Form gegeben sind, die eine Anwendung auf alle Arten von Kegelschnitten gestattet, und dass dabei der Einwirkung des bewegten Körpers auf die Sonne, wovon der Factor √(1+μ) abhängt, Rechnung getragen ist. Wenn wir diese Gesetze als Erscheinungen betrachten, die aus unzähligen und unzweifelhaften Beobachtungen sich ergeben haben, so lehrt die Geometrie, welche Einwirkung von der Sonne auf die um Letztere bewegten Körper ausgeübt werden muss, um jene Erscheinungen beständig hervorzubringen. Auf diese Weise findet sich, dass die Einwirkung der Sonne auf die um sie laufenden Körper ganz so ausgeübt wird, als ob eine Anziehungskraft, deren Stärke dem Quadrate der Entfernung wechselseitig proportional wäre, die Körper gegen den Mittelpunkt der Sonne hintriebe. Geht man daher umgekehrt von der Annahme einer solchen Anziehungskraft als von einem Principe aus, so können jene Erscheinungen als nothwendige Folgen daraus abgeleitet werden. Hier mag eine blosse Erwähnung der Gesetze genügen, und es wird um so weniger erforderlich sein, an diesem Orte bei ihrem Zusammenhange mit dem Princip der Schwere zu verweilen, da seit dem grossen Newton noch mehre andere Schriftsteller jene Materie behandelt haben, und unter diesen Laplace in seinem vollendeten Werke "Mécanique Céleste" in einer Weise, die nichts zu wünschen übrig lässt.

3.

Die Untersuchungen der Bewegungen der Himmelskörper, so weit solche in Kegelschnitten vor sich gehen, erfordern keineswegs eine vollständige Theorie dieser Art von Curven, und es wird daher eine einzige allgemeine Gleichung genügen, aus der wir Alles ableiten. Es erscheint deshalb sachgemäss, gerade die Gleichung auszuwählen, auf welche wir als eine charakteristische bei Erforschung der zufolge des Attractionsgesetzes beschriebenen Curve Bezug nehmen. Wenn wir nämlich irgend einen Ort des Körpers in seiner Bahn bezeichnen durch die Abstände x und y von zwei geraden Linien, die in der Ebene der Bahn gezogen sind und im Mittelpunkte der Sonne d. h. in dem einen der beiden Brennpunkte der Curve unter rechten Winkeln sich schneiden; und wenn wir ausserdem die Entfernung eines Körpers von der Sonne (stets positiv genommen) mit r benennen, so haben wir zwischen r, x, y die lineare Gleichung r + α·x + β·y = γ; in welcher α, β, γ beständige Grössen ausdrücken, und zwar γ eine Grösse, die ihrer Natur nach stets positiv ist. Indem wir nun die Lage der geraden Linien, auf welche die Abstände x und y sich beziehen, verändern (eine Lage die an und für sich ganz willkürlich ist, wenn es nur dabei bleibt, dass sich die Linien unter rechten Winkeln schneiden), so wird dadurch offenbar die Form der Gleichung und der Werth von γ nicht geändert, während α und β immer andere und wieder andere Werthe erlangen und man sieht, dass jene Lage so bestimmt werden kann, dass β = 0 wird, α aber wenigstens nicht negativ. — Schreibt man solchergestalt für α und γ beziehungsweise e und p, so nimmt obige Gleichung die Gestalt an r + e·x = p. Die gerade Linie, auf welche in diesem Falle die Abstände y bezogen werden, heisst die Apsidenlinie, p der halbe Parameter, e die Excentricität, und der betreffende Kegelschnitt wird mit dem Namen Ellipse, Parabel oder Hyperbel bezeichnet, je nachdem e kleiner als die Einheit, gleich der Einheit, oder grösser als die Einheit ist.

Uebrigens sieht man leicht, dass die Lage der Apsidenlinie durch die vorgetragenen Bedingungen voll­ständig bestimmt ist, den einzigen Fall ausgenommen, wo sowohl α als β schon an und für sich = 0 waren. In diesem Falle wird stets r = p, auf welche geraden Linien die Abstände x und y auch bezogen werden. Indem daher e ebenfalls = 0 ist, so wird die Curve (die dann ein Kreis ist) nach unserer Begriffs­bestimmung dem Genus der Ellipsen beizuzählen sein, hat aber das Eigenthümliche, dass die Lage der Apsiden gänzlich willkürlich bleibt, wenn man anders jene Bezeichnung auch auf diesen Fall auszudehnen belieben sollte.

4.

Für den Abstand x wollen wir jetzt den Winkel ν einführen, der zwischen der Apsidenlinie und der geraden Linie (radius vector) enthalten ist, die von der Sonne nach dem Orte des Körpers führt, und zwar möge dieser Winkel von derjenigen Seite der Apsidenlinie beginnen, wo die Abstände x positiv sind. Auch werde angenommen, dass dieser Winkel nach derjenigen Gegend hin wachse, wohin die Bewegung des Körpers gerichtet ist. Auf diese Weise wird x = r·cos ν, und demnach unsere Formel r = 1/(1 + e·cos ν), woraus sich folgende Schlüsse unmittelbar ableiten lassen:

  1. Für ν = 0 wird der Werth des radius vector ein Kleinstes, nämlich r = p/(1 + e); dieser Punkt heisst das Perihel.
  2. Den entgegengesetzten Werthen von ν entsprechen gleiche Werthe von r; die Apsidenlinie theilt daher den Kegelschnitt in zwei gleiche Theile.
  3. In der Ellipse wächst von ν = 0 an r beständig, bis es den grössten Werth (r = p/(1 - e) im Aphel erreicht, für welches ν = 180°. Nach Passirung des Aphels nimmt r auf dieselbe Weise wieder ab, wie es früher gewachsen war, bis es für ν = 360° das Perihel von Neuern berührt. Derjenige Theil der Apsidenlinie, welcher an dieser Stelle vom Perihel und an jener vom Aphel begrenzt wird, heisst die grosse Axe. Es wird daher die grosse Halbaxe, welche auch die mittlere Entfernung genannt wird, = p/(1 - ee). Der Abstand des inmitten der Axe belegenen Punktes (des Mittelpunkts der Ellipse) vom Brennpunkte ist = ep/(1 - ee) = ea, wobei a die grosse Halbaxe bezeichnet.
  4. Dagegen existirt in der Parabel eigentlich kein Aphel, sondern r wächst über alle Grenzen hinaus, je näher ν an +180° oder -180° herankommt. Für ν = +180° wird der Werth von r unendlich, was anzeigt, dass die Curve von der Apsidenlinie in dem, dem Perihele gegenüber liegenden Theile nicht geschnitten wird. Es kann daher im eigentlichen Sinne hier von einer grossen Axe, oder von einem Mittelpunkte der Curve nicht die Rede sein; aber nach der gewöhnlichen Manier der Analysis wird durch Erweiterung der für die Ellipse erfundenen Formeln der grossen Axe ein unendlicher Werth beigelegt, und der Mittelpunkt der Curve wird in unendliche Entfernung vom Brennpunkte gesetzt.
  5. In der Hyperbel schliesslich wird ν in noch engere Grenzen eingezwängt, nämlich innerhalb ν = -(180° - ψ) und ν = +(180° - ψ); wo ψ einen Winkel bezeichnet, dessen Cosinus = 1/e. Denn während ν sich einem dieser Grenzwerthe nähert, wächst r ins Unendliche fort; und wenn für ν einer dieser Grenzwerthe selbst angenommen würde, so würde der Werth von r als ein unendlicher herauskommen, was anzeigt, dass die Hyperbel von einer geraden Linie, die gegen die Apsidenlinie unter einem Winkel von 180° - ψ oberhalb oder unterhalb geneigt ist, überall nicht geschnitten wird. Für die solchergestalt ausgeschlossenen Werthe, nämlich von 180° - ψ bis zu 180° + ψ, weist unsere Formel dem r einen negativen Werth an; denn die gerade Linie, die unter einem solchen Winkel gegen die Apsidenlinie geneigt ist, schneidet selbst zwar die Hyperbel nicht, wenn sie jedoch rückwärts verlängert wird, so trifft sie das andere Stück der Hyperbel, welches bekanntlich von dem ersten Stücke überall getrennt und gegen denjenigen Brennpunkt hin, welchen die Sonne einnimmt, convex ist. Aber in unserer Untersuchung — welche, wie schon erwähnt, auf der Voraussetzung beruht, dass r positiv genommen werden soll, — nehmen wir auf dieses zweite Stück der Hyperbel keine Rücksicht, worin nur ein solcher Himmelskörper einherziehen könnte, auf den die Sonne nicht attractiv, sondern nach denselben Gesetzen repulsiv wirken würde. Im eigentlichen Sinne des Worts giebt es daher auch in der Hyperbel kein Aphel. Als das Analogon des Aphels könnte derjenige Punkt des abgekehrten Stücks genommen werden, welcher auf der Apsidenlinie liegt und welcher den Werthen ν = 180°, r = - p/(e - 1) entspricht. Will man daher wie bei der Ellipse den Werth des Ausdrucks p/(1 - ee) auch hier, wo er negativ sich ergiebt, die halbe grosse Axe der Hyperbel nennen, so zeigt diese Grösse die Entfernung des bereits erwähnten Punktes vom Perihel und zugleich seine Lage an, welche in der Ellipse die entgegengesetzte Stelle einnimmt. Ebenso erhält hier e·p/(1 - ee) d. h. der Abstand des mittleren Punktes zwischen diesen beiden Punkten (Centrums der Hyperbel) vom Brennpunkte einen negativen Werth wegen der entgegengesetzten Lage.

5.

Der Winkel ν, welcher in der Parabel zwischen den Grenzen -180° und +180°, für die Hyperbel innerhalb -(180° - ψ) und +-(180° - ψ) eingeschlossen ist, bei der Ellipse aber den ganzen Kreis in stets erneuten Perioden durchläuft, heisst die wahre Anomalie des bewegten Körpers. Bislang pflegten zwar fast alle Astronomen die wahre Anomalie in der Ellipse nicht vom Perihel, sondern vom Aphel an zu zählen, gegen die Analogie der Parabel und der Hyperbel, in denen es kein Aphel giebt, und man daher vom Perihel anfangen musste. Wir haben indess um so weniger Bedenken getragen, eine Analogie zwischen allen Arten von Kegelschnitten herzustellen, da die neusten französischen Astronomen dazu mit dem Beispiele vorangegangen sind.

Im Uebrigen ist es mitunter dienlich, die Form des Ausdrucks p/(1 + e·cosν) etwas zu ändern. Vorzüglich merke man sich folgende Formeln:

  • Formel
  • Formel

In der Parabel hat man daher:

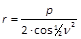  • Formel;

in der Hyperbel aber ist folgender Ausdruck besonders bequem:

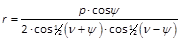  • Formel.

6.

Wir wollen jetzt zur Vergleichung der "Bewegung" mit der "Zeit" schreiten. Wenn man, wie in Art. 1, den innerhalb der Zeit t um die Sonne beschriebenen Flächenraum = ½·g setzt, die Masse des bewegten Körpers = μ (die Sonnenmasse = 1 gesetzt), so haben wir: g = k·t√p·√(1 + μ). Das Differential des Flächenraums aber wird ½r·r·dψ, woraus hervorgeht: k·t√p·√(1 + ψ) = ∫r·r·dν, wobei dies Integral so genommen wird, dass es für t = 0 verschwindet. Diese Integration muss für die verschiedenen Arten von Kegelschnitten auf verschiedene Weise behandelt werden, weshalb wir das Einzelne getrennt betrachten, und den Anfang mit der Ellipse machen wollen.

Da r aus ν mittelst eines Bruches bestimmt wird, dessen Nenner aus zwei Gliedern besteht, so wollen wir vor allen Dingen diese Unbequemlichkeit durch Einführung einer neuen Grösse für ν beseitigen. Zu diesem Zwecke setzen wir

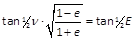
  • Formel
  • wonach die letzte Formel im vorhergehenden Artikel für r giebt:
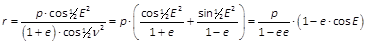  • Formel.
  • Ferner wird
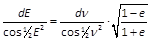
  • Formel
  • und daher
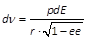
  • Formel
  • hieraus
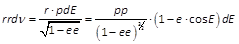  • Formel;
  • und wenn man integrirt:
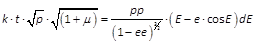  • Formel.

Wenn wir daher die Zeit vom Durchgange durch das Perihel an beginnen lassen, wo ν = 0, E =  0 und daher auch Constans = 0, so haben wir, weil p ⁄ (1 - ee) = a,

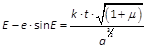  • Formel;

Bei dieser Gleichung muss der Hülfswinkel E, welcher die excentrische Anomalie heisst, in Theilen des Halbmessers ausgedrückt werden. Offenbar aber lässt sich dieser Winkel in Graden etc. beibehalten, wenn man nur auch e · sin E und

  • Formel

auf dieselbe Art ausdrückt; diese Grössen werden in Bogensecunden erhalten, wenn man sie durch die Zahl 206264,81 multiplicirt. Der Multiplication der letzteren Grösse bleibt man überhoben, falls man sogleich die Grösse k in Secunden darstellt anwendet, und daher setzen wir an Stelle des früheren Werthes k = 3548″,18761, dessen log = 3,5500065746. — Auf diese Weise ausgedrückt heisst die Grösse

  • Formel

die mittlere Anomalie, die daher im Verhältnis der Zeit wächst und zwar täglich um das Augment

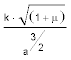  • Formel,

welches man die mittlere tägliche Bewegung (motus medius diurnus) nennt. — Die mittlere Anomalie bezeichnen wir durch M.

7.

Im Perihele sind daher die wahre Anomalie, die excentrische Anomalie und die mittlere Anomalie = 0. — Indem nun von hieran die wahre Anomalie wächst, so werden auch die excentrische und die mittlere jedoch so vermehrt, dass die excentrische kleiner bleibt, als die wahre, und die mittlere kleiner als die excentrische, bis zum Aphel, wo alle drei zugleich = 180° werden; von hieran aber bis zum Perihel ist die excentrische immer grösser als die wahre, und die mittlere Anomalie grösser als die excentrische, bis im Perihel alle drei = 360° werden, oder was auf dasselbe herauskommt, alle wiederum = 0. Im Allgemeinen ist klar, dass, wenn einer wahren Anomalie ν eine excentrische E und eine mittlere M entspricht, dann einer wahren von 360° - ν eine excentrische von 360° - E und eine mittlere von 360° - M entspricht. Der Unterschied, zwischen der wahren Anomalie und der mittleren ν - M heisst die Gleichung des Mittelpunkts (aequatio centri), welche daher vom Perihel bis zum Aphel positiv, vom Aphel bis zum Perihel negativ ist, im Perihele und Aphele selbst aber verschwindet. Da nun also ν und M den vollen Kreis von 0 bis zu 360° in der nämlichen Zeit durchlaufen, so wird die Zeit eines einmaligen Umlaufs, welche auch die periodische Zeit (tempus periodicum) heisst, in Tagen ausgedrückt gefunden, wenn man 360° durch die tägliche Bewegung (k√(1+μ)) / a3/2 dividirt; woraus man sieht, dass für die verschiedenen, um die Sonne revolvirenden Körper die Quadrate der periodischen Umlaufszeiten den Cuben der mittleren Entfernungen proportional sind, in soweit es erlaubt ist, deren Massen, oder vielmehr die Ungleichheit der Massen zu vernachlässigen.

8.

Nun wollen wir die bemerkenswerthesten Relationen zwischen den Anomalien und dem radius vector sammeln, deren Ableitung Niemandem, der nur mittelmässig in der trigonometrischen Analyse bewandert ist, Schwierigkeiten darbieten kann. Die Formeln werden concinner [harmonischer], wenn man für e den Winkel einführt, dessen Sinus = e ist. Wird dieser Winkel mit φ bezeichnet, so hat man:

  • Formel

Die vorzüglichsten Relationen zwischen a, p, r, e, φ, ν, E, M sind folgende:

  1. p = a·cos φ2
  2. r = p ⁄ (1 + e·cos ν)
  3. r = a·(1 - e·cos E)
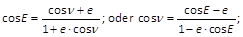
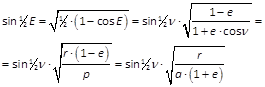
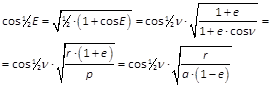
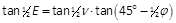
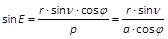
  4. Formel
  5. Formel
  6. Formel
  7. Formel
  8. Formel
  9. r·cos ν = a·(cos E - e) = 2·a·cos(½·E + ½·φ + 45°)·cos(½·E - ½·φ - 45°)
  10. sin ½·φ·sin ν·√(r/p) = sin ½·φ·sin E·√(a ⁄ r)
  11. sin ½·(ν + E) = cos ½·φ·sin ν·√(r/p) = cos ½·φ·sin E·√(a ⁄ r)
  12. M = E - e·sin E.

9.

Verlängert man ein, aus irgend einem Punkte der Ellipse auf die Apsidenlinie gefälltes Perpendikel rückwärts, bis es einen aus dem Mittelpunkte der Ellipse mit dem Halbmesser = a beschriebenen Kreis trifft, so wird die Neigung desjenigen Halbmessers, der dem Einschneidepunkte entspricht, gegen die Apsidenlinie (ähnlich verstanden, wie vorhin für die wahre Anomalie) der excentrischen Anomalie gleich sein, wie sich ohne Mühe aus der Gleichung IX im vorhergehenden Artikel ableiten lässt. Man sieht ferner, dass r·sin ν den Abstand eines jeden Punktes der Ellipse von der Apsidenlinie bezeichnet; und da dieser Abstand nach Gleichung VIII = a·cos φ·sin E ist, so wird er seinen grössten Werth bei E = 90° erreichen, d. h. im Mittelpunkte der Ellipse. Dieser grösste Abstand, der = a·cosφ = p / cos φ = √(a·p) heisst die halbe kleine Axe. Im Brennpunkte der Ellipse, d. h. für ν = 90°, wird jener Abstand offenbar = p, oder gleich dem halben Parameter.

10.

Die Gleichungen des Art. 8 enthalten Alles, was zur Berechnung der excentrischen Anomalie und der mittleren aus der wahren, oder der excentrischen und der wahren aus der mittleren erforderlich ist. Um die excentrische aus der wahren abzuleiten, bedient man sich gewöhnlich der Formel VII. Gemeiniglich jedoch empfiehlt es sich, zu diesem Zwecke die Gleichung X zu benutzen, besonder sobald die Excentricität nicht zu gross ist in welchem Falle E mit grösserer Schärfe aus X berechnet werden kann, als ans VII. Ausserdem hat man bei Anwendung der Gleichung X den Logarithmus des Sinus von E, der in XII gebraucht wird, sofort durch die Gleichung VIII, welcher bei Anwendung von VII erst aus den Tafeln genommen werden müsste; wenn daher bei jener Methode der fragliche Logarithmus gleichfalls den Tafeln entnommen wird, so erlangt man dadurch eine Prüfung für die Richtigkeit der Rechnung. Derartige Rechnungsprüfungen und Bestätigungen sind stets überaus schätzbar, und uns bei denselben Raths zu erholen, wird daher bei allen in diesem Werke abzuhandelnden Methoden, da wo es bequem geschehen kann, unsere eifrige Sorge sein. Zur besseren Erläuterung fügen wir ein vollständig berechnetes Beispiel hinzu:

Gegeben sei ν = 310° 55′ 29″ 64, φ = 14° 12′ 1″ 87, log r = 0,3307640; Gesucht werden: p, a, E und M.

log sin φ 9,3897262  
log cos ν 9,8162877  
  9,2060139 woraus e·cos ν = 0,1606993
log (1 + e·cos ν) 0,0647197  
log r 0,3307640  
log p 0,3954837  
log cos φ2 9,9730448  
log a 0,4224389  
log sin ν 9,8782740-  
log √(p/r) 0,0323598.5  
  9,8459141.5-  
log sin ½φ 9,0920395
log sin ½·(ν - E) 8,9379536.5- also ½·(ν - E) = -4° 58′ 94″ 94;
ν - E = -9° 56′ 45″ 88; E = 320° 52′ 15″ 52

Ferner wird   Rechnung für log sin E nach Formel VIII.
log e 9,389 7262 log r⁄p sin ν 9,8135543
log 206 264,8 5,314 4251 log cos φ 9,9865224
log e in Sec 4,704 1513 log sin E 9,8000767
log sin E 9,800 0767 n  
  4,504 2280 n also e sin E in Sec. = 31932" 14 = 8° 52′ 14
und M = 329° 44′ 66 Rechnung für log sin E nach Formel VII.
  ½ν = 155° 27′ 82 log tang ½ν 9,6594579
  45° - ½φ = 37° 53′ 59" 065 log tang (45° - ½φ) 9,8912427
 
  log tang ½E 9,5507006
woraus ½E = 160° 26′ 7" 76 und E = 320° 52′ 15" 52, wie oben.

11.

Die umgekehrte, unter dem Namen des Kepler'schen Problems berühmte Aufgabe, nämlich aus der mittleren Anomalie die wahre und den radius vector zu finden, kommt weit häufiger zur Frage. Die Astronomen pflegen die Gleichung des Mittelpunktes durch eine unendliche, nach den Sinussen der Winkel M, 2M, 3M etc. fortschreitende Reihe darzustellen, wobei die einzelnen Coefficienten der Sinusse ebenfalls Reihen sind, die nach den Potenzen der Excentricität in's Unendliche fortlaufen. Ich habe es um so weniger für nothwendig erachtet, mich bei dieser von mehrern Schriftstellern entwickelten Formel für die Gleichung des Mittelpunktes hier aufzuhalten, weil sie, wenigstens nach meinem Urtheile, für den praktischen Gebrauch, namentlich wenn die Excentricität nicht sehr klein ist, viel weniger geeignet ist, als die indirecte Methode, welche ich daher in der Form, die mir die bequemste scheint, etwas näher erörtern will.

Die Gleichung XII, E = M + e·sin E, die transcendent ist und eine directe Auflösung nicht zulässt, wird durch Versuche aufgelöst, indem man mit einem genäherten Werthe von E beginnt, der durch geeignete, so oft wiederholte Methoden corrigirt wird, bis er jener Gleichung genau Genüge thut, d. h. entweder mit aller der Genauigkeit, welche die Sinustafeln zulassen, oder doch mit der, welche dem vorgesteckten Ziele entspricht. Wenn nun jene Correctionen nicht blindlings, sondern nach einer sicheren und bestimmten Norm angestellt werden, so besteht kaum ein wesentlicher Unterschied zwischen einer solchen indirecten Methode und der Auflösung durch Reihen, wenn nicht darin, dass bei jener der erste Werth der Unbekannten einigermaassen willkürlich ist, was eher für einen Gewinn gelten kann, da ein schicklich ausgewählter Werth es erlaubt, die Verbesserungen ausserordentlich zu beschleunigen. Setzen wir voraus, dass ε ein genäherter Werth von E sei, und x die jenem hinzuzufügende (in Secunden ausgedrückte) Verbesserung, so dass der Werth E = ε + x unserer Gleichung genau Genüge thut. Man berechne e·sin E in Secunden durch Logarithmen, und bemerke bei dieser Ausführung zugleich aus den Tafeln die Aenderung von log sin ε für 1″ durch die Variation von ε, sowie die Veränderung des log e·sin ε für die Aenderung einer Einheit in der Zahl e·sin ε; diese Veränderungen mögen ohne Rücksicht auf die Zeichen λ, μ sein, wobei es kaum nöthig ist, daran zu erinnern, dass dabei jeder Logarithmus durch gleich viele Decimalstellen ausgedrückt vorausgesetzt wird. Wenn nun schon ε dem wahren Werthe von E bereits so nahe kommt, dass man die Veränderungen des Logarithmus des Sinus von ε bis zu ε + x, und die Veränderungen des Logarithmus der Zahl von e·sin ε bis zu e·sin (ε + x) als einförmige annehmen kann, so lässt sich offenbar setzen: e·sin (ε + x) = e·sin ε ±(λ·x / β), wobei das obere Zeichen für den ersten und vierten Quadranten, das untere für den zweiten und dritten gilt. — Es sei daher ε + x = M + e·sin (ε + x), so wird x = (β / (β -/+ α))·(M + e·sin β - β) und der wahre Werth von E, oder von β + x = M + e·sin β±(α / (β-/+α)·(M + e·sin β - β) wobei die Zeichen in angegebener Weise bestimmt werden. Uebrigens sieht man leicht, dass ohne Rücksicht auf das Zeichen β:α = 1:e·cos β und daher immer β grösser als α, woraus geschlossen wird, dass im ersten und letzten Quadranten M + e·sinβ zwischen β und β + x, dass aber im zweiten und dritten β + x zwischen β und β + x liegt; eine Regel, welche uns der Beachtung der Zeichen überhebt. Weicht der vorausgesetzte Werth von β noch zu sehr von der Wahrheit ab, als dass die vorhin erwähnte Voraussetzung genau genug sein sollte, so wird man wenigstens durch diese Methode einen viel näheren Werth finden, mit welchem man die nämliche Operation noch einmal und so oft es nöthig scheint, zu wiederholen hat. Es ist ohne Weiteres klar, dass, wenn der Unterschied des ersten Werthes für β vom wahren, als eine Grösse der ersten Ordnung angesehen wird, der Fehler des neuen Werthes zur zweiten Ordnung gehört und durch Wiederholung der Operation zur vierten, achten etc. Ordnung heruntergebracht wird. Desto kleiner überdies die Excentricität ist, desto schneller werden die successiven Verbesserungen convergiren.

12.

Ein genäherter Werth für E, von welchem man bei der Rechnung ausgehen kann, wird gemeiniglich zur Hand sein, besonders falls die Aufgabe für mehre Werthe von M zu lösen ist, von denen einige schon absolvirt sind. In Ermangelung aller anderen Hülfsmittel constirt aber wenigstens soviel, dass E zwischen den Grenzen M und M ± e liegen muss (wo e die in Secunden ausgedrückte Excentricität bezeichnet und wobei das obere Zeichen im ersten und zweiten Quadranten, das untere im dritten und vierten genommen wird). Es kann daher für den Anfangswerth von E entweder M, oder ein Werth angenommen werden, der nach irgend welcher Schätzung vermehrt oder vermindert ist. Kaum braucht erwähnt zu werden, dass die erste Rechnung, sobald man von einem wenig genauen Werthe ausgeht, keine ängstliche Genauigkeit erfordert, und dass kleinere Logarithmentafeln, z. B. die von Lalande, völlig ausreichen. Ausserdem kann man zur Bequemlichkeit der Rechnung immer solche Werthe für β wählen, deren Sinus aus den Tafeln selbst ohne Interpolation sich entnehmen lässt, z. B. in Minuten oder in vollen Zehnern der Secunden, je nachdem die angewandten Tafeln in Minuten, oder von zehn zu zehn Secunden fortschreiten. Uebrigens kann Jeder leicht diejenigen Modificationen entwickeln, welche jene Vorschriften für den Fall erleiden, dass die Winkel in der neuen Decimaleintheilung ausgedrückt sind.

13.

Beispiel: Es sei die Excenticität dieselbe wie im Beispiel zu Art. 10. M = 332° 28′ 54" 77. Hier ist daher log e in Secunden = 4,7041513 und deshalb e = 50600" = 14 ° 3′ 20" da nun hier E kleiner sein uss als M, so setzen wir zur ersten Rechnung ε = 326°, wofür man aus den kleineren Tafeln erhält:
  log sin ε 9,74756 Veränderung für 1′...19, also λ = 0,312
  log sin e in Sec, 4,70415  
 
 
  4,45171  
hieraus e sin ε = -28295" = -7° 51′ 40" Verändeung des Logarithmus für eine Tafeleinheit, die hier 10" begleicht, 15,25; also μ = 1.525.
Differirt von ε um 1° 22′ 40" = 4960", folglich 0,312⁄1,213 · 4960" = 1276" = 21′ 16 ". Hiermit wird der verbesserte Werth von E = 324° 37′ 20" - 21′ 16" = 324° 16′ 4", mit welchen man die Rechnung nach grösseren Tafeln wiederholt.
  log sin ε 9,7664112 λ = 29,25  
  log e 4,7041513  
 
 
  4,4705624 μ = 146  
  e sin ε = -29550" 34 = -8° 12′ 30" 43  
  M + e sin &epsilon   324° 16′ 24" 43  
  Differirt von ε um -20" 43.  
Multiplizirt man diese Differenz durch λ⁄(μ-λ) = 29,25⁄116,75, so erh&äuml;lt man - 5" 12 und daher ist der aufs Neue verbesserte Werth für E = 324° 16′ 24" 43 + 5" 12 = 324° 16′ 29" 55, innerhalb 0" 01 genau.

14.

Zur Bestimmung der wahren Anomalie und des radius vector aus der excentrischen Anomalie geben die Gleichungen des Art. 8 mehre Methoden an die Hand, von denen wir die vorzüglichsten erläutern wollen.

  1. Nach der gewöhnlichen Methode wird ν durch die Gleichung VII und dann r durch die Gleichung II bestimmt. Auf diese Weise steht das Beispiel des vorhergehenden Artikels, wenn man den für p in Art. 10 gegebenen Werth beibehält, so:
    ½E = 162° 8′ 14" 75   log e 9,3897262
    log tang ½E 9,5082198 log cos ν 9,8496597
    log tang (45° - ½φ) 9,8912427   9,2393859
    log tang ½ν 9,6169771 e cos ν = 0,1735345
    ½ν = 157° 30′ 41" 50 log p 0,3954837
    ν = 315° 1′ 23,00 log (1 + e cos ν) 0,0694959
     
      log r 0,3259878
  2. Kürzer ist folgende Methode, wenn mehrere Orte zu berchnen sind, für welche man die constanten Logarithmen der Grössen √a(1+e), √a(1-e) nur einmal zu berechnen braucht. Aus den Gleichungen V und VI erhält man
    • sin ½ν√r = sin ½E√a(1+e)
    • cos ½ν√r = cos ½E√a(1-e)
    wodurch ½ν und log√r schnell bestimmt werden. Im Allgemeinen wird allerdings — sobald man Psin Q = A, Pcos Q = B hat — Q durch die Formel tang Q = A⁄B gefunden, und dann ist hiernach P = A⁄sinQ oder P = B⁄cosQ. Die erstere wendet amn an, wenn sinQ grösser ist als cosQ ist; die zweite, wenn cosQ grösser als sinQ ist. Gemeiniglich schliessen die Aufgaben, bei welchen man zu solchen Gleichungen gelangt, (wie dieselben denn in diesem Werke sehr häufig vorkommen) die Bedingung in sich, dass P eine positive Grösse sein muss, und dann wird im Zweifel, ob Q innerhalb 0° bis 180°, oder von 180° - 360° zu nehmen ist, von selbst beseitigt. Ohne das Vorhandensein einer solchen Bedingung aber bleibt diese Bestimmung unserem Ermessen überlassen.
    In underem Beispiel haben wir e = 0,2453162,
    log sin½E 9,4867632 log cos½E 9,9785435
    log√a(1+e) 0,2588593 log√a(1-e) 0,1501020
    Hieraus
    log sin ½ν√r 9,7456225 log tang ½ν 9,6169771
    log cos ½ν√r 0,1286454 ½ν = 157° 30′ 41" 50
    log cos ½ν 9,9656515   ν = 315° 1′ 23,00
    		 
    log √r 0,1629939  
    log r 0,3259878  
  3. Diesen Methoden fügen wir eine dritte hinzu, welche beinahe ebenso kurz, als die zweite, dieser aber da, wo die ässerste Genauigkeit verlangt wird, meistens vorzuziehen ist. Zuerst wird nämlich r durch die Gleichung III, und sodann ν aus X bestimmt. Unser af diese Weise behandeltes Beispiel steht dann so:
    log e 9,3897262 log sin E 9,7663366
    log cos E 9,9094637 log √(1 - e cosE) 9,9517744
      9,2991899   9,8145622
    e cos E = 0,1991544 log sin ½φ 9,0920395
    log a 0,4224389 log sin½(ν - E) 8,9066017
    log (1- e cos E) 9,9035488 ½(ν - E) = - 4° 37′ 33" 24
    		 
    log r 0,3259877 ν - E -9° 15′ 6" 48
      ν = 315° 1′ 23" 02
    Zur Prüfung der rechnung ist die Formel VIII oder XI sehr bequem, vorzüglich wenn ν und r durch die dritte Methode bestimmt sind. Hier folgt die Rechnung:
    log a⁄r sin E 9,8627878 log sin E√a⁄r 9,8145622
    log cos φ 9,9865224 log cos ½φ) 9,9966567
      9,8493102   9,8112189
    log sin ν 0,8493102 log sin ½(ν+E) 9,8112189

14.

Zur Bestimmung der wahren Anomalie und des radius vector aus der excentrischen Anomalie geben die Gleichungen des Atr. 8 mehrere Methoden an die hand, von denen wir die vorzüglochsten erläutern wollen.

  1. Nach der gewöhnlichen Methode wird ν durch die Gleichung VII und dann r durch die Gleichung II bestimmt. Auf diese Weise steht das Beispiel des vorhergehenden Artikels, wenn man für p den in Art. 10 gegebenen Werth beibehält, so:
    ½E = 162° 8′ 14" 75. log e 9,3897262
    log tang ½E 9,5082198 log cos ν 9,8496597
     
    log tang(45° - ½ φ) 9,812427   9,2393859
    		 
    log tang ½ ν 9,6169771 e cos ν = 0,1735345
     
    ½ ν = 157° 30′ 41" 50 log p 0,3954837
    ν = 315° 1′ 23,00" log (1 + e cos ν) 0,0694959
     
      log ν 0,3259878
  2. Kürzer ist folgende Methode, wenn mehre Orte zu berechnen sind, für welche man die constanten Logarithmen der Gössen √a(1+e), √a(1-e) nur einmal zu berechnen braucht. Aus den Gelichungen V und VI erhält man

    • Formel
    • Formel



    wodurch ½ν und log √r schnell bestimmt werden. Im allgemeinen wird allerdings — sobald man P sinQ = A, P cosQ = B hat — Q durch die Formel tang Q = A ⁄ b gefunden, und dann ist hiernach P = A ⁄ sinQ oder P = B ⁄ cosQ. Die Erstere wendet man an, wenn sinQ grösser als cosQ ist; die zweite, wenn cosQ grösser als sinQ ist. Gemeiniglich schliessen die Aufgaben, bei welchen man zu solchen Gleichungen gelangt, (wie dieselben denn in diesem Werke sehr häufig vorkommen) die Bedingung in sich, dass P eine positive Grösse sein muss, und dann wird der zweifel, ob Q innerhalb 0° bis 180°, oder von 180° - 360° zu nehmen ist, von selbst beseitigt. Ohne das Vorhandensein einer solchen Bedingung aber bleibt diese Bestimmung unserem Ermessen überlassen.
    In unserem Beispiele haben wir e = 0,2453162,
    log sin ½E 9,4867632 log cos ½ E 9,9785434
    log √a(1+e) 0,2588593 log √a(1-e) 0,1501020
    Hieraus
    log sin ½ ν √r 9,7456225 log tang ½ ν 9,6169771
    log cos ½ ν √r 0,1286454
    log cos ½ ν 9,9656515 ½ ν = 157° 30′ 41" 50
    log cos ½ ν 9,9656512 ν = 315° 1′ 23,00"
    		 
    log √r 0,1629939  
    log r 0,3259878  

  3. Diesen Methoden fügen wir eine dritte hinzu, welche beinahe so kurz, als die zweite, dieser aber da, wo die äusserste Genauigkeit verlangt wird, meistens vorzuziehen ist. Zuerst wird nämlich r durch die Gleichung III, sodann ν aus X bestimmt. Unser auf diese Weise behandeltes Beispiel steht dann so:

    log e 9,3897262 log sin E 9,7663366
    log cos E 9,9094637 log √( 1 - e cos E) 9,9517744
      9,9221899   9,8145622
    e cos E = 0,1991544 log sin ½ φ 9,0920395
    log a 0,4224389 log sin ½ (ν - E) 9,9066017
    log (1 - e cos E) 9,9035488 ½ (ν - E) - 4° 37′ 33" 24
    		ν-E - 9° 15′ 6" 48
    log r 0,3259877 ν 315° 1′ 23" 02

    Zur Prüfung der Berechnung ist die Formel VIII oder XI sehr bequem, vorzüglich wenn ν und r durch die dritte Methode bestimmt sind. Hier folgt die Rechnung:

    log a⁄r sin E 9,8627878 log sin E √a ⁄ r 9,8145622
    log cos φ 9,9865224 log cos ½ φ 9,9966567
      9,8493102   9,8112189
    log sin ν 9,8493102 sin ½ (ν + E) 9,8112189

15.

Da die mittlere Anomalie M, wie wir gesehen haben, durch ν und φ vollständig bestimmt wird, und ebenso ν durch M und φ, so is klar, dass, wenn alle drei Grössen zugleich als veränderliche betrachtet werden, unter ihren differentialen Aenderungen eine Bedingungsgleichung Statt finden müsse, deren Erforschung nicht überflüssig erscheint. Indem man zuerst die Gleichung VII im Art. 8 differentiiert, erhält man

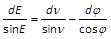  • Formel;

differentiiert man nun auch die Gleichung XII, so folgt dM = (1 - e·cos E) dE - sin E cos φ dφ. Eliminirt man aus diesen Differentialgleichungen dE, so resultiert

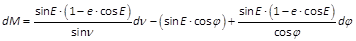
  • Formel
  • oder, falls man für sin E und für 1 - e cos E ihre Werthe aus den Gleichungen VIII und III substituiert:
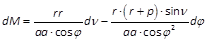
  • Formel
  • oder endlich, wenn man jeden Coefficienten nur durch ν und φ ausdrückt:
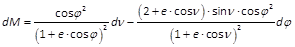  • Formel.
  • Betrachtet man umgekehrt ν als eine Funktion der Grössen M und φ, so erhält die Gleichung folgende Form:
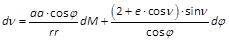
  • Formel
  • oder durch Einführung von E statt ν
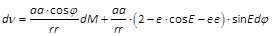
  • Formel

16.
Quelle
Carl Friedrich Gauss: Theorie der Bewegung der Himmelkörper, welche in Kegelschnitten die Sonne umlaufen. Ins deutsche übertragen von Carl Haase. Hannover 1865.
Valid HTML 4.01 © Rainer Stumpe URL: http://www.rainerstumpe.de