Der Ellipsen-Parameter

Der "Ellipsenparameter" geht auf Apollonios von Perge zurück, der in seinem Buch De Conicis die Kegelschnitte — Ellipse, Parabel und Hyperbel — untersucht, und ihre geometrischen Eigenschaften untersucht. Für die Ellipse und ihren Umkreis findet er, dass alle Sehnen, die auf der großen Achse senkrecht stehen und Kreis und Ellipse schneiden, sich die Kreissehnen- und die Ellipsensehnenabschnitte wie die große zur kleinen Halbachse der Ellipse verhalten. Der Abschnitt der Ellipsensehne, die durch den Brennpunkt geht, heißt "Ellipsenparameter".

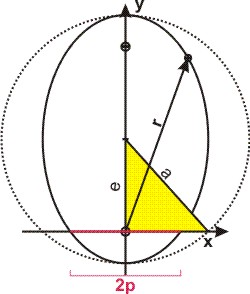Die Länge der halben Kreissehne kann man nach dem Satz des Pythagoras im rechtwinkligen, gelb gefüllten, Dreieck berechnen. Da der Abstand des Brennpunktes der Ellipse von deren Mittelpunkt gleich der linearen Exzentrizität e ist, und die Länge der Hypothenuse des Dreiecks gleich dem Radius a des Umkreises (oder der großen Halbachse) ist, hat die halbe Kreissehne s_K die Länge s_K = √(a² - e²).
Die halbe Ellipsensehne p verhält sich zur halben Kreissehne s_K wie die kleine zur großen Halbachse b bzw. a der Ellipse: p ⁄ s_K = b ⁄ a, oder nach p aufgelöst und eingesetzt: p =  b ⁄ a · √(a² - e²).
Und da die Definition der linearen Exzentrizität e lautet: e² = a² - b², ergibt sich:

p = b² ⁄ a.

Die lineare Gleichung

Gauss will in seinem Buch eine allgemeine Formel für die Bewegung von Körpern auf Bahnen be­schrei­ben, die Kegelschnitte sind. Seit Kepler war nämlich vermutet worden, dass sich z. B. Kometen auf Parabeln oder Hyperbeln bewegen. Die Bahnparameter aus wenigen Punkten zu berechnen ist zur Unterscheidung der Bahnformen wichtig. Edmond Halley hatte zwar 1682 für den nach ihm benannten Kometen (Umlaufperiode 76 Jahre) die elliptische Bahn nachgewiesen, aber es gab Kommeten, die noch nicht zweimal beobachtet worden waren.

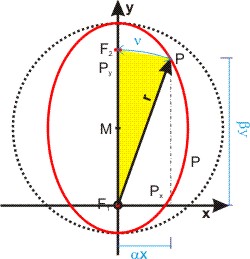
Gauss beschreibt ein Anordnung der Ellipse mit der Ap­sidenlinie, auf der die Brenn­punkte liegen, als y-Achse. Die x-Achse schneidet die Apsidenlinie in dem Brenn­punkt der Ellipse, in dem die Sonne steht. Der Abstand r des Punktes P vom Ursprung des Koor­dinatensystem ist der radius vector. Er schließt mit der Apsidenlinie den Winkel ν ein. Der Winkel wird vom sonnennächsten Punkt, dem Perihel, aus gemessen.

Er postuliert nun eine lineare Gleichung: r + αx + βy = γ. Hierbei ist r der Fahrstrahl vom Brennpunkt F₁ zum Punkt P auf der Ellipsenbahn, x und y sind die karthesischen Koordinaten des Punktes P_{x, y}, und γ eine Konstante für alle Punkte P. Die Faktoren α und β haben die Werte α·x = PF₁ = r₁, und β·x = PF₂ = r₂.
Die postulierte lineare Formel drückt also den Zusammenhang für den Umfang U des Dreiecks ΔF₁F₂P aus, der für eine gegebene Ellipse konstant ist, da aus der Definition r₁ + r₁ = 2·a (a ist die große Halbachse), und der Abstand der beiden Brennpunkte F₁F₂ = 2·e (e ist die lineare Exzentrizität).

Aus der Konstanten γ — oder U — kann man für bestimmte Lagen die Koordinaten x, y von P berechnen: steht P auf der x-Achse, so ist P_x = r₁ = p, der Ellipsenparameter und P_y = 0. r₂ ergibt sich dann aus dem rechtwinkligen Dreieck r₂ = √(p² + e²).

Im Absatz 4 geht Gauss nun zur Diskussion des Eigenschaften des Polarkoordinatensystems der Kegelschnitte mit dem Brennpunkt als Ursprung ein. Der Fahrstrahl (radius vector) r und der Winkel ν sind die Koordinaten. Die x-Koordinate des Punktes P wird in Polarkoordinaten ersetzt durch x = r·cos ν. Einsetzen in die lineare Gleichung führt zu dem Azsdruck: r = 1 ⁄ (1 + e·cos ν).