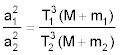Die keplerschen Gesetze
Zeichnet man die von der Erde aus beobachteten Bewegungen der inneren Planeten unseres Sonnensystems relativ zum Fixsternhimmel auf, so beobachtet man seltsame Schleifenbewegungen. Diese Schleifen waren mit den geozentrischen Theorien nur sehr schwer zu erklären.
Johannes Kepler wertete die Planetenbeobachtungen seines Lehrers Tichio Brahe aus, und stellte fest, die Planetenbahnen lassen sich verstehen, wenn man annimmt, dass sie sich nicht auf Kreisen, sondern auf Ellipsen um die Sonne bewegen.
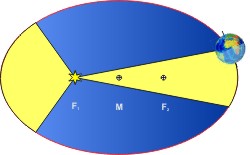
Eine Ellipse hat einen Mittelpunkt M und zwei Brennpunkte F1,2. Für jeden Punkt auf der Ellipse ist die Summe der Abstände zu den beiden Brennpunkten konstant. Die Ellipse wird beschrieben durch die große und die kleine Halbachsen (auf der großen Achse liegen der Mittelpunkt und die beiden Brennpunkte, die kleine steht senkrecht darauf und geht durch den Mittelpunkt), a und b, und die Exzentizizät e (das ist der Abstand jedes Brennpunktes zum Mittelpunkt).
- Keplersches Gesetz:
Die Planeten bewegen sich auf Ellipsen um die Sonne, die in einem der beiden Brennpunkte steht. - Keplersches Gesetz:
Die von der Sonne zum Planeten gezogenen Fahrstrahlen überstreichen in gleichen Zeiträumen gleiche Flächen. - Keplersches Gesetz:
Die Quadrate der Umlaufzeiten der Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen ihrer Bahnellipsen.
Das erste und das zweite Gesetz gelten exakt, wenn man statt der Sonne den Schwerpunkt des Systems Sonne-Planet in den Brennpunkt der Bahnellipse setzt. Sie sind in der Kepler Gleichung ausgedrückt. Das dritte vernachlässigt die Planetenmasse gegenüber der Sonnenmasse; seine exakte Form lautet:
Eine unangenehme Begleiterscheinung der elliptischen Planetenbahnen ist, dass die Umlaufgeschwindigkeit der Erde um die Sonne (wegen des 2. Keplerschen Gesetzes) nicht konstant ist. Wenn die Erde im Winter näher an der Sonne steht ist ihre Geschwindigkeit größer als im Sommer, wenn sie weiter von der Sonne entfernt ist. Deshalb ist der Sonnentag (die Zeit zwischen zwei Mittagshöchstständen der Sonne über einem Punkt der Erde) im Winter etwas länger als im Sommer (da die Erde eine größere Strecke auf ihrer Bahn zurücklegt muss sie sich ein Stückchen weiter drehen, bis die Somme wieder den Höchststand erreicht hat). So sind die Sonnentage im Winter etas länger.
Kepler bewies die elliptische Form der Bahnen von Himmelskörpern um ein Zentralgestirn empirisch: seine Planetenortberechnungen waren einfach exakt. Isaak Newton konnte das dann mit der Erfindung eine neuen Kraft, die zwischen Zentralgestirn und Planet wirkt: der Gravitation erklären. Es blieb das Problem der Nichtlösbarkeit der Mondbahnberechnung (das drei Körperproblem).
