An Appendix concerning the Description and Use of a small Portable Quadrant, for the more easie finding of the Hour and Azimuth, and Other Astronomical and Geometrical Conclusions.
CHAP. II.
Of the Use of the Quadrant, in taking the Altitude of the Sun, Moon, and Stars.
The Quadrant is the fourth part of a Circle divided equally into 90 gr. and here numbred by 10, 20, 30, &c unto 90 gr. each degree being subdivided into 4.
Lift up the Center of the Quadrant so as the Thred with the Plummet may play easily by the Side of it, and the Sun-beams may pass through both Sights; so shall the Degrees cut by the Thred shew what is the Altitude at the time of observation, as may appear by this Example.
Upon the 14 day of April, about Noon, the Sun-beams passing through bot Sights, the Thred fell upon 51 gr. 20 m. and this was the true Meridian Altitude of the Sun for that day, in this Latitude of 51 gr. 30 m. for which the Quadrant was made.
Again, toward three of the Clock in the afternoon, the Thred fell upon 38 gr. 40 m. and such was the Suns Altitude at that time.
CHAP. III.
Of the ECLIPTICK.
1. The Place of the Sun being given, to find his Right Ascension.
The Ecliptick is here represented by the Ark figured with the Characters of the 12 Signs, ♈, ♉, ♊, &c. each Sign being divided unequally into 30 gr. and they are to be reckoned from the Character of the Sign.
Let the Thred be laid on the place of the Sun in the Ecliptick, and the Degrees which it cutteth in the Quadrant shall be the Right Ascension required.
As if the place of the Sun given be the fourth Degree of ♊, the Thred laid on this Degree shall cut 62 gr. in the Quadrant, which is the Right Ascension required. But if the place of the Sun given be more than 90 gr. from the beginning of ♈, there must be more than 90 gr. allowed to the Right Ascension; for this Instrument is but a Quadrant. And so if the Sun be in 26 gr. of ♋, yozu shall find the Thred to fall in the same place, and yet the Right Ascension to be 118 gr.
2. The Right Ascension of the Sun being given, to find his Place in the Ecliptick.
Let the Thred be laid on the Right Ascension in the Quadrant, and it shall cross the place of the Sun in the Ecliptick, as may appear in the former Example.
CHAP. IV.
Of the Line of Declination.
The Line of Declination is here drawn from the Center to the beginning of the Quadrant, and divided from the beginning of ♈ downward into 23 gr. 30 m.
Let the Thred be laid, and the Bead set on the Place of the Sun in the Ecliptick; then move the Thred to the Line of Declination, and there the Bead shall fall upon the Degrees of the Declination required.
As if the place of the Sun given be the fourth Degree of ♊; the Bead first set to this place, and then moved to the Line of Declination, shall there shew the Declination of the Sun at the time to be 21 gr. from the Equator.
2. The Declination of the Sun being given, to find his place in the Ecliptick.
Let the Thred and Bead be first laid to the Declination, and then moved to the Ecliptick.
As if the Declination be 21 gr. the Bead first set to this Declination, and then moved to the Ecliptick, shall shew the fourth of ♊, the fourth of ♐, the 26 of ♋, and the 26 of ♑; and which of these four is the place of the Sun, may appear by the Quarter of the Year.
CHAP. V.
Of the Circle of Months and Days.
This Circle is here represented by the Ark figured with these Letters, J, F, M, A, M, &c. signifying the Months January, February, March, April, &c. each Month divided unequally, according to the number of Days that are therein.
| Dies. | 0 | 5 | 10 | 15 | 20 | 25 | 30 | |||||||
| Mens. | Gr. | M. | Gr. | M. | Gr. | M. | Gr. | M. | Gr. | M. | Gr. | M. | Gr. | M. |
| January | 292 | 20 | 297 | 46 | 303 | 7 | 308 | 21 | 313 | 30 | 318 | 36 | 323 | 36 |
| February | 324 | 35 | 329 | 28 | 334 | 16 | 339 | 1 | 343 | 42 | 348 | 21 | ||
| March | 351 | 17 | 355 | 52 | 0 | 26 | 4 | 58 | 9 | 30 | 14 | 2 | 18 | 34 |
| April | 19 | 30 | 24 | 4 | 28 | 42 | 33 | 23 | 38 | 5 | 42 | 52 | 47 | 42 |
| May | 47 | 42 | 52 | 35 | 57 | 32 | 62 | 34 | 67 | 39 | 72 | 45 | 77 | 52 |
| June | 78 | 55 | 84 | 5 | 89 | 17 | 94 | 28 | 99 | 30 | 104 | 48 | 109 | 55 |
| July | 109 | 55 | 115 | 0 | 120 | 0 | 124 | 58 | 129 | 54 | 134 | 45 | 139 | 30 |
| August | 140 | 27 | 145 | 9 | 149 | 48 | 154 | 25 | 159 | 0 | 163 | 32 | 168 | 0 |
| Septemb. | 168 | 57 | 173 | 26 | 177 | 56 | 182 | 26 | 186 | 56 | 191 | 28 | 196 | 5 |
| October | 196 | 5 | 200 | 45 | 205 | 25 | 210 | 12 | 215 | 3 | 220 | 0 | 225 | 0 |
| Novemb. | 226 | 2 | 231 | 10 | 236 | 23 | 241 | 40 | 247 | 2 | 252 | 30 | 258 | 2 |
| Decemb. | 258 | 2 | 263 | 35 | 269 | 8 | 274 | 42 | 280 | 16 | 285 | 46 | 291 | 15 |
1. The Day of the Month being given, to find the Altitude of the Sun at Noon.
Let the Thred be laid to the Day of the Month, and the Degrees which it cutteh in the Quadrant shall be the Meridian Altitude required.
As if the Day given be the 15 of May, the Thred laid on this day shall cut 59 gr. 30 m. in the Quadrant, which is the Meridian Altitude required.
2. The Meridian Altitude being given, to find the Day of the Month.
The Thred being set to the Meridian Altitude, doth also fall on the day of the Month.
As if the Altitude at Noon be 59 gr. 30 m. the Thred being set to his Altitude, doth fall on the 15 of May, and the 9 of July; and which of these two is the true day, may be known by the quarter of the year, or by another days Observation. For if the Altitude prove greater, the Thred will fall on the 16 day of May, and the 8 of July; or if it prove lesser, the Thred will fall on the 14 of May, and the 10 of July; whereby the question is fully answered.
CHAP. VI.
Of the Hour-lines.
That Ark which is drawn upon the center of the Quadrant by the beginning of Declination, doth here represent the Equator: That Ark which is drawn by 23 gr. 30 m. of Declination, and is next above the Circle of Months and Days, representeh the Tropicks: Those Lines which are between the Equator and the Tropicks, being undivided, and numbered at the Equator by 6, 7, 8, 9, 10, 11, 12; at the Tropick by 1, 2, 3, 4, &c. do represent the Hour-circles: That which is drawn from 12 in the Equator to the middle of June, representeh the Hour of 12 at Noon in the Summer; and those which are drawn with it to the right hand, are the Hours of the Day in the Summer, and the Hours of the Night in the Winter: That which is drawn from 12 in the Equator, to the middle of December, representeth the Hour of 12 in the Winter; and those which are drawn with it to the left hand, are the Hours of the Day in the Winter, and the Hours of the Night in the Summer; and of both these, that which is drawn from 11 to 1 serves for 11 in the forenoon, and 1 in the afternoon; that which is drawn from 10 to 2, serves for 10 in the forenoon, and 2 in the afternoon: for the Sun on the same Day is about the same height two Hours before Noon, as two Hours after Noon. The like reason holdeth for the rest of the Hours.
1. The Day of the Month, or the Height at Noon being known, to find the Place of the Sun in the Ecliptick.
The Thred being laid to the day of the Month, or the height at Noon, (for one gives the other by the former Proposition) mark where it crosseth the Hour of 12, and set the Bead to that Intersection; then move the Thred till the Bead fall on the Ecliptick, and it shall fall on the place of the Sun.
As if the day given be the 15 of May, or the Meridian Altitude 58 gr. 30 m. lay the Thred accordingly, and put the Bead to the Intersection of the Thred with the Hour of 12; then move the Thred till the Bead fall on the Ecliptick, and it shall there shew the fourth of ♊, the fourth of ♐, the 26 of ♋, and the 26 of ♑; and which of these is the place of the Sun may appear by the Quarter of the Year, or another days observation.
2. The place of the Sun in the Ecliptick being known, to find the Day of the Month.
Let the Thred and Bead be first laid on the place of the Sun in the Ecliptick, and then moved to the Line of 12.
As if the place of the Sun given be the fourth of ♊, the Bead being laid to this Degree, and then moved to the Hour of 12 in the Summer, the Thred will fall on the 15 day of May, and the 9 of July; or or if it be moved to the Hour of 12 in the Winter, the Thred will fall on the 6 of January, and the 16 of November; which of these is the day of the Month required, may appear by the Quarter of the Year.
In this and the former Proposition you have two ways to rectifie the Bead, by the place of the Sun, and by the days of the Month: the better way is by the place of the Sun; for in other, the Leap-year may breed some small difference.
There is yet a third way: For Seamen having a Table for the Declination on each day of the year, may set the Bead thereto in the Line of Declination.
3. The Hour of the Day being given, to find the Altitude of the Sun above the Horizon.
The Bead being set for the time by either of three ways, let the Thred be moved from the Hour of 12 toward the Line of Declination, till be Bead fall on the Hour given; and the Degrees which it cuts in the Quadrant, shall shew the Altitude of the Sun at that time.
As if the time given be the 10 of April, the Sun being then in the beginning of ♉, the Bead being rectified, you shall find the Height at Noon 50 gr. 0 m. at 11 in the morning 48 gr. 12 m. at 10 but 43 gr. 12 m. at 9 but 36 gr.at 8 but 27 gr. 30 m. at 7 but 18 gr. 18 m. at 6 but 9 gr. at 5 it meeteth with the Line of Declination, and hath no Altitude at all, and therefore you may think it did rise much about that Hour.
Then if you move the Thred again from the Line of Declination toward the Hour of 12, you shall find that the Sun is 8 gr. 33 m. below the Horizon at 4 in the morning, and near 16 gr. at 3, and 21 gr. 51 m. at 2, and 25 gr. 40 m. at 1, and 27 gr. at midnight.
4. The Altitude of the Sun being given, to find the Hour of the Day.
The Altitude being observed as before, let the Bead be set for the time, then bring the Thred to the Altitude, so the Bead shall shew the Hour of the day.
As if the 10 of April, having set the Bead for the time, you shall find by the Quadrant the Altitude to be 36 gr. the Bead at the same time will fall upon the Hour-line of 9 and 3; wherefore the Hour is 9 in the forenoon, or 3 in the afternoon. If the Altitude be near 40 gr. you shall find the Bead at the same time to fall half way between the Hour-line of 9 and 3, and the Hour-line of 10 and 2; wherefore it must be either half an Hour past 9 in the morning, or half an Hour past 2 in the afternoon; and which of these is the true time of the day, may be soon known by a second Observation: for if the Sun rise higher, it is the forenoon; if it become lower, it is the afternoon.
5. The Hour of the Night being given, to find how much the Sun is below the Horizon.
The Sun is always so much below the Horizon at any Hour of the Night, as his opposite Point is above the Horizon at the like Hour of the Day; and therefore the Bead being set, if the question be made of nay Hour of the Night in the Summer, then move it to the like Hour of the Day in the Winter; if of any Hour of the Night in Winter, then move it to the like Hour of the Day in Summer: so the Degrees which the Thred cutteth in the Quadrant shall shew how much the Sun is below the Horizon at that time.
As if it be required to know how much the Sun is below the Horizon the 10 of April at 4 of the Clock in the Morning, the Bead being set to his place according to the time in the Summer-hours, bring it to 4 of the Clock in the afternoon in the Winter-hours, and so shall you find the Thred to cut 8 gr. and about 30 m. in the Quadrant; and so much is the Sun below the Horizon at that time.
6. The Depression of the Sun supposed, to give the Hour of the Night with us, or the Hour of the Day to our Antipodes.
Here also, because the Sun is so much above the Horizon at all Hours of the day, as his opposite point below the Horizon at the like Hour of the Night; therefore first set the Bead according to the time, then bring the Thred to the Degree of the Suns Depression below the Horizon, so shall the Bead fall on the contrary Hour-lines, and there shew the Hour of the Night in regard of us, which is the like Hour of the Day to our Antipodes.
As if the 10 of April, the Sun being then in the beginning of ♉, and by supposition 8 gr. 30 m. below the Horizon in the East, it be required to know what time of the Night it is; first, set the Bead according to the Day in the Summer-hours, then bring the Thred to 8 gr. 30 m. in the Quadrant, so shall the Bead fall among the Winter-hours on the Line of 4 of the Clock in the afternoon: wherefore to our Antipodes it is 4 on the Clock in their afternoon, and to us it is then 4 of the Clock in the morning.
7. The time of the Year, or the place of the Sun being given, to find the beginning of Day-break, and end of Twilight.
This Proposition differeth little from the former: for the Day is said to begin to break when the Sun commeth to be 18 gr. below our Horizon in the East; and Twilight to end, when it is gotten 18 gr. below the Horizon in the West: Wherefore let the Bead be set for the time, and then bring the Thred to 18 gr. in the Quadrant, so shall the Bead fall on the contrary Hour-lines, and there the Hour of Twilight, as before.
So if it be required to know at what time the Day begins to break on the 10 of April, the Sun being then in the beginning of ♉; first, set the Bead according to the time in the Summer-hours, and then bring the Thred to 18 gr. in the Quadrant, so shall the Bead fall among the Winter-hours a little more than a quarter before 3 in the morning; and that is the time when the Day begins to break upon the 10 of April.
CHAP. VII.
Of the Horizon.
The Horizon is here represented by the Ark drawn from the beginning of Declination toward the end of February, divided unequally, and numbered by 10, 20, 30, 40, &c.
1. The Day of the Month, or the Place of the Sun being known, to find the Amplitude of the Suns Rising and Setting.
Let the Bead rectified for the time be brought to the Horizon, and there it shall shew the Amplitude required.
As if the day given be the 15 of May, the Sun being in the fourth Degree of ♊, the Bead rectified and brought to the Horizon, shall there fall on 35 gr. 8 m. such is the Amplitude of the Suns Rising from the East, and of his setting from the West; which Amplitude is always North when the Sun is in the Northern Signs, and when he is in the Southern Signs always Southward.
2. The Day of the Month, or the Place of the Sun being given, to find the Ascensional Difference.
Let the Bead rectified for the time be brought to the Horizon, so the Degrees cut by the Thred in the Quadrant shall shew the difference of Ascension.
As if the day given be the 15 of May, the Sun being in the fourth Degree of ♊, let the Bead rectified and brought to the Horizon; so shall the Thred in the Quadrant shew the Ascensional difference to be 28 gr. and about 50 m.
Upon the Ascensional difference depends this Corollary.
To find the Hour of the Rising and Setting of the Sun, and thereby the length of Day and Night.
The time of the Suns Rising may be guessed at by the 3 of the last Chapter; but here by the Ascensional difference it may be better found and that to a minute of time. For if the Ascensional Difference be converted into time, allowing an Hour for 15 gr. and 4 Minutes of an Hour for each degree, it it sheweth how long the Sun riseth before six of the Clock in the Summer, and after six in the Winter.
As if the day given be the 15 of May, the Sun being in the fourth Degree of ♊, and his Ascensional Difference found as before 28 gr. 50 m. this converted into time, maketh 1 ho. And somewhat near 55 m. of an Hour: wherefore the Sun at that time, in regard it was Summer, rose 1 ho. And full 55 m. before 6 of the clock; and so having the quantity of the Semidiurnal Ark, the length of the day and Night need not be unknown.
CHAP. VIII.
Of the Five Stars.
I might have put in more Stars, but these may suffice fort he finding of the Hour of the Night at all times of the Year: And first I make choice of Ala Pegasi, a Star in the extremity of the Wing of Pegasus, in regard it wants but 6 minutes of time of the beginning of ♈; but because it is but of the second magnitude, and not always to be seen, I made choice of four more, one for each quarter of the Ecliptick, as Oculus ♉, The bulls Eye, whose Right Ascension converted into time, is 4 ho. 15 m. then of Cor ♌, The Lions Heart, whose Right Ascension is 9 ho. 48 m. next of Arcturus, whose Right Ascension is 13 ho. 58 m. and lastly of Aquitha, or The Vultures Heart, whose Right Ascension is 19 ho. 33 m. These five Stars have all of them Northern Declination; and if any others, some of these will be seen at all times of the Year. The use of them is,
The Altitude of any of these five Stars being known, to find the Hour of the Night.
First, put the Bead to the Star which you intend to observe, take his Altitude, and find how many Hours he is from the Meridian by the fourth Prop. of the sixth Chap. Then out of the Right Ascension of the Star, take the Right Ascension of the Sun converted into Hours, and mark the difference, for this difference being added to the observed Hour of the Star from the Meridian, shall shew how many Hours the Sun is gone from the Meridian, which is in effect the Hour of the Night.
As if the 15 of May, the Sun being in the fourth Degree of ♊, I should set the Bead to Arcturus, and observing his Altitude, should find him to be in the West about 52 gr. high, and the Bead to fall on the Hour-line of 2 afternoon, the Hour would be 11 ho. 50 m. past noon, or 10 m. short of midnight.
For, 62 gr. the Right Ascension of the Sun, converted into time, makes 4 ho. 8 m. which if we take out of 13 ho. 58 m. the Right Ascension of Arcturus, the difference will be 9 ho. 50 m. and this being added to 2 ho. The observed distance of Arcturus from the Meridian, shews the Hour of the Night to be 11 ho. 50 m. Another Example will make all more plain.
If the 9 of July, the Sun being then in 26 gr. of ♋, I should set the Bead of Oculus ♉, and observing his Altitude, should find him to be in the East about 12 gr. high, and the Bead to fall on the Hour-line of 6 before Noon, which is 18 ho. Past the Meridian, the Hour of the Night would be better than a quarter past 2 of the clock in the morning.
For, 118 gr. the Right Ascension of the Sun, converted into time, make 7 ho. 52 m. this taken out of 4 ho. 15 min. the Right Ascension of Oculus ♉, adding a whole Circle, (for otherwise there could be no subtraction) the difference will be 20 ho. 23 m. and this being added to 18 ho. Which was the observed distance of Oculus ♉ from the Meridian, shews that the Sun (abating 24 ho. for the whole Circle) is 14 ho. 23 m. past the Meridian, and therefore 23 m. past 2 of the clock in the morning.
If the Nocturnal be placed on the back side of the Quadrant, you may avoid this Equation of Right ascensions. For knowing the time of the Year when the Star will be in the South at midnight, you may bring that time to the Hour observed, then will the Day of the Month wherein you made the Observation point at the Hour of the Night required. As in the first Example, where, on the 15 of May, the Bead set to Arcturus fell on the Hour-line of 2 in the afternoon, because Arcturus will be in the South the 14 of October complete at midnight, you may place the 14 of October^at the Hour of 2, so the 15 of May will point to 11 ho. 50 m.
In the second Example, where the 9 of July the Bead set to the Bulls Eye fell on the Hour-line of 6 before Noon, because the Bulls Eye will be in the South the 16 of May complete at midnight, you may turn the 16 of May to the Hour of 6, and so shall find the 9 of July to point 2 ho. 23 m. as before.
CHAP. IX.
Of the Azimuth-line.
Those Lines which are drawn between the Equator and the Tropicks, on that side of the Quadrant which is nearest unto the Sights, and are numbred by 10, 20, 30, &c. do represent the Azimuths: the uttermost towards the left hand representeth the Meridian; that which is numbred with 20, the twentieth: and so the rest. These Lines which are drawn from the Equator to the left hand, do shew the Azimuth in the Summer; and those other to the right hand do shew the same in the Winter. The Use of them is:
1. The Azimuth wherein the Sun beareth from us being known, to find the Altitude of the Sun above the Horizon.
First, let the Bead be set for the time, as in the former Chapter; then move the Thred until the Bead fall on the Azimuth: so the Degrees which the Thred cutteh in the Quadrant shall shew the Altitude of the Sun at that time. Where you are to observe, That seeing the Azimuths are drawn on the right side of the Quadrant, you are also to begin to number the Degrees of the Suns Altitude from the right hand toward the left: As if the Sights had been set on the Line AB, and you had turned your right hand towards the Sun in observing of his Altitude, contrary to our practice in the former Chapter.
As if the time given were 2 of August, when the Sun hath about 15 gr. of North Declination, you may set the Bead for the time, so you shall find the Height at Noon, when the Sun is in the South, to be 53 gr. 20 m, when he is 10 gr. from the South 53 gr. 10 m. when 20 gr. then about 52 gr. 8 m. when 30 gr. then 50 gr. 20 m. when 40 gr. then 47 gr. 48 m. when 50 gr. then 44 gr. 12 m. when 60 gr. then 39 gr. 35 m. when 70 gr. then 33 gr. 50 m. when 80 gr. then 17 gr. when he is in the East or West 90 gr. from the Meridian, then is the height near 19 gr. 20 m. and before he cometh to the Azimuth of 320 gr, he hath no Altitude. For the Sun having 15 gr. of North Declination, will rise and set at 114 gr. 34 m. from the Meridian.
2. The Altitude of the Sun being given, to find on what Azimuth he beareth from us.
Let the Bead be set for the time, and the Altitude observed as before; then bring the Thred to the Complement of that Altitude, so the Bead shall shew the Azimuth required.
As if the second of August, having set the Bead for the time, you shall find the Altitude of the Sun to be 19 gr. 20 m. remove the Thred unto 70 gr. 40 m. the Complement of the Altitude; or, which is all one, to 19 gr. 20 m. from the right hand toward the left, and the Bead will fall on the Line of 90 gr. from the Meridian; and therefore the Point whereon the Sun beareth from us is one of these two, either due East, or due West: And which of these is the true Point of the Compass, may be soon known by a second Observation; for if the Sun rise higher, it is the forenoon; if it be lower, it is the afternoon.
By knowing the Azimuth or Point of the Compass whereon the Sun beareth from us, it is easie to find,
- A Meridian Line, and thereby
- The Coasting of the Countrey,
- The Site of a Building,
- The Variation of the Compass.
As if the second of August in the afternoon I should find by the Height of the Sun that he bears from me 60 gr. from the Meridian toward the West; then there being 90 gr. belonging to each quarter, the West will be 30 gr. to the right hand; the East is opposite to the West, the North and South lie equally between them.
CHAP. X.
Of the Quadrat.
The Quadrat hath two Sides divided; the other two Sides next the Center may be supposed to be divided each of them into 100 equal parts: That which is next the Horizontal line contains the parts of Right Shadow; the other next the Sights, the parts of Contrary Shadow. The Use of the Quadrat is,
1. Any Point being given, to find whether it be level with the Eye.
Lift up the center of the Quadrant, so that the Thred with the Plummet may play easily by the Side of it: then look through the Sights to the Place given; for now if the Thred shall fall on AB the Horizontal-line, then is the Place given level with the Eye: But if it shall fall within the said Line on any of the Divisions, then it is higher; if without, then it is lower than level of the Eye.
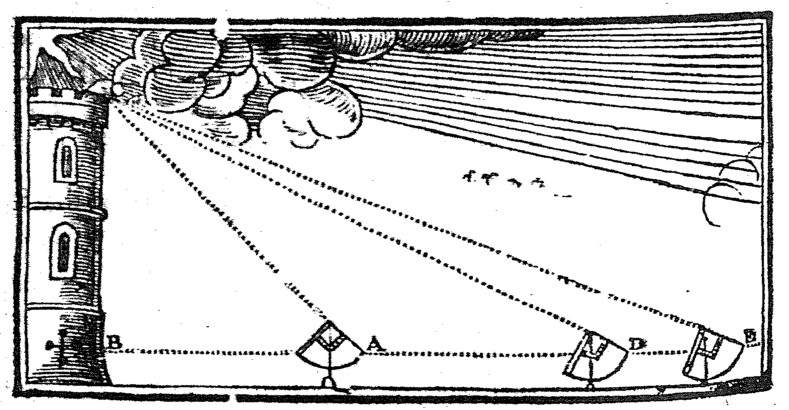
2. To find an Height above the level of the Eye, or a Distance at one Observation.
Look through the Sights to the Place, going nearer or farther from it, till the Thred fall on 100 parts in the Quadrat of 45 gr. in the Quadrant, so shall the Height of the Place above the Level of the Eye, be equal to the Distance between the Place and the Eye.
If the Thred fall on 50 parts of a Right Shadow, the Height is but half the Distance: If it fall on 25, it is a quarter of the Distance; if on 75, it is three quarters of the Distance. For as oft as the Thred falleth on the parts of the Right Shadow.
- As 100, to the Parts on which the Thred falleth:
- So is the Distance, to the Height required.
And on the contrary,
- As the Parts cut by the Thred are to 200:
- So the Height, unto the Distance.
But when the Thred shall fall on the parts of Contrary Shadow, if it fall on 50 parts, the Height is double unto the Distance; if on 25, it is four times as much as the Distance. For as oft as the Thred falleth on the parts of Contrary Shadow,
- As the Parts cut by the Thred, are unto 100:
- So is the Distance, unto the Heights.
And on the contrary,
- As 100, are unto the Parts cut by the Thred:
- So is the Height, unto the Distance.
And what is here said of the height and Distance, the same may be understood of the Height and Shadow.
3. To find a Height or a Distance at two Observations.
As if the Place which is to be measured might not otherwise be approached, and yet it were required to find the Height BC and the Distance: First, I make choice of a Station at A, where the Thred may fall on 100 parts in the Quadrat, and 45 gr. in the Quadrant, the Distance AB will be equal to the Height BC: then if I go farther in a direct Line with the former Distance, and make choice of a second Station at D, where the Thred may fall on 50 parts of Right Shadow, the Distance BD should be double the height BC; wherefore I may measure the difference between the two Stations A and D, and this difference DA will be equal both to the Distance AB; and the Height BC.
Or if I cannot make choice of such Stations, I take such as I may, one at D, where the Thred falleth at 50 parts of Right Shadow; the second at E, where it falleth on 40 parts; and supposing the height BC to be 100, I find that,
- As 50 Parts are unto 100, the Side of the Quadrat:
- So 100 the suopposed Height, unto 200 the Distance DB.
- And as 40 parts at the second Station, unto 100:
- So 100 the supposed Height, unto 250 the Distance BE.
Wherefore the difference between the Stations D and E should seem to be 50; and then if in the measuring of it I should find it to be either more or less, the Proportion will hold, As from the supposed Difference, to the measured difference; so from Height to height, and from Distance to Distance.
As if the difference between the two Stations D and E being measured, were found to be 30,
- As 50 the supposed difference, unto 30 the true difference:
- So 100 to supposed height, unto 60 the true Height:
- And 200 the supposed Distance, unto 120 the true Distance:
- And 250 at the second Station, unto 150 the Distance BE.
The like reason holdeth in all other Examples of this kind. And if an Index with Sights were fitted to turn upon the Center, it might then serve by the same reason for the finding of all other Distance.
Finis.