Rechnen mit dem Rechenschieber
Mit dem Rechenschieber addiert und subtrahiert man Strecken auf den logarithmisch geteilten Skalen, die abwechselnd auf Körper und Zunge liegen. Nach ein wenig Übung muss man nicht mehr nachdenken: es geht "wie von allein".
Multiplizieren
Die Multiplikationsaufgabe 75,35 · 4,81 löst man mit dem Rechenschieber in folgenden Schritten:
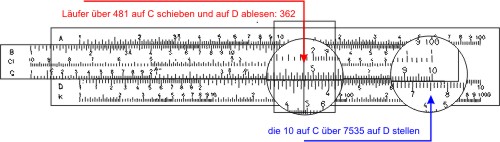
Man stellt das Ende der Zungenskala C über die größere Zahl auf der Körperskala D (auf D ist nun die Strecke 7,535 abgegriffen) und schiebt den Läufermittelstrich auf die Zahl 4,81 auf der Zungenskala C. Dadurch ist die Strecke 4,81 agegriffen. Nun liest man auf D die Länge der addierten Strecken ab: 362. Nun müssen die Kommastellen im Kopf abgeschätzt werden: 70 · 5 ist 350, also lautet das Ergebnis 362.
[Zurück]
Dividieren
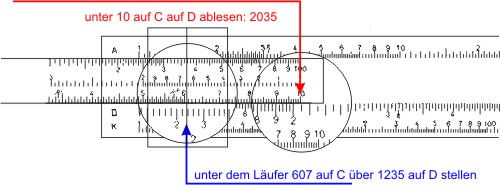
Die Divisionsaufgabe 123,5 : 60,7 löst man durch abziehen zweier Strecken in zwei Schritten:
Wieder werden die Kommastellen im Kopf abgeschätzt: 120 : 60 ist 2 ⇒ das Ergebnis ist 2,035.
[Zurück]
Dreisatzaufgaben
Eine typische Aufgabe des Alltages für den Rechenschieber ist die Dreisatzrechnung oder Proportionalität. Häufig werden Haushaltsprodukte in verschiebenen Packungsgrößen angeboten — die Erfahrung lehrt, nicht immer ist die größere Menge auch die billigste. Von einem Spülmittel gibt es zwei Packungsgrößen: 110 Einheiten zu 19,99 € und 160 Einheiten zu 34,99 €
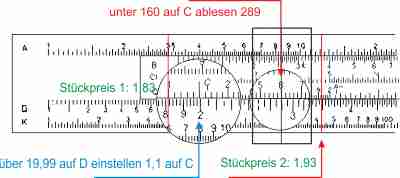
Man stellt über den Preis (19,99) auf der Köperskala D die Anzahl (110) auf der Zungenskala C, und schiebt den Läufer über die andere Verpackungsgröße (160) auf Skala C. Man liest auf D ab: beim gleichen Stückpreis dürfte die größere Packung nur etwa 29,00 € kosten. Der Stückpreis der größeren Packung liegt bei über 0,193 €. Den Stückpreis der kleineren Packung findet man unter der 1 auf C: 0,182 €.
Andere Verpackungsgrößen vergleicht man durch Verschieben des Läufers.
[Zurück]
Ketten rechnen
Mit etwas Übung und Planung kann man Kettenaufgabe mit dem Rechenschieber schnell lösen. Dabei achtet man darauf, dass die Zunge nicht unnötig hin- und hergeschoben wird. Als Regel kann man sich merken: erst dividieren, dann multiplizieren. Eine Kettenaufgabe ist z. B. der Bruch
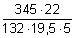 .
.
Zunächst ordnet man die Zahlen so, dass übereinander stehende Paare auf den Rechenschieberskalen C und D möglichst nahe stehen:
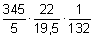 .
.
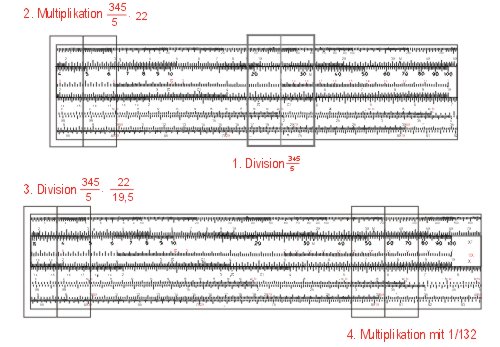
Zuerst stellt man 5 auf C über 345 auf D, verschiebt den Läufer über 22 auf C und verschiebt dann die Zunge, so dass 195 auf C unter dem Läuferstrich steht. Nun kommt der Trick: statt den Läufer auf 10 (C) zu verschieben und 5 auf der Zungenskala C unter den Läuferstrich zu stellen, multipliziert man mit der Skala CI auf der Zunge, d.h. mit 1 ⁄ 132. Dazu bewegt man den Läuferstrich auf 132 der Skala CI. Das Ergebnis 591 liest man auf D ab. Die Kommastelle findet man überschlagsmäßig:
- 300 · 20 = 6000,
- 6000 ⁄ 100 = 60,
- 60 ⁄ 20 = 3,
- 3 ⁄ 5 = 0,6.
- Das Ergebnis der Kettenrechnung ist 0,591.
[Zurück]
Rechnung mit den Quadratskalen
Wenn man eine zurückgelegte Strecke in km oder sm und die für die Fahrt benötigte Zeit in Minuten kennt, gibt es einen hübschen Trick mit dem Rechenschieber: man spart sich eine Multiplikation.
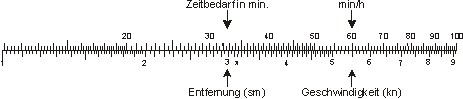
Die Geschwindigkeit v berechnet man durch Division von Weg a und Zeit t : v = a ⁄ t. Man dividiert also die Fahrtstrecke durch die Fahrtzeit — und erhält km ⁄ min oder sm ⁄ min. Das Ergebnis muss man nun mit 60 multiplizieren. Auf den Quadratskalen ( von 1 bis 100) des Rechenschiebers kommt aber eine "60" vor. Also dividieren wir mit den Skalen A und B, und lesen das Ergebnis nicht unter der 1 von A ab, sondern unter der "60": so haben wir gleich mit 60 multipliziert, und brauchen keine Kommastellen abzuschätzen.
Hat unser Segelboot also für 9 ½ Seemeilen 75 Minuten gebraucht, entspricht das eine Geschwindigkeit von 7,6 Knoten.
Will man dagegen wissen, wann man bei einer gegebenen Geschwindigkeit im 3 sm entfernten Hafen ankommt, so stellt man die Geschwindigkeit (5,5 kn) unter die 60 auf A und liest den Zeitbedarf über der Entfernung ab: knapp 33 min.
[Zurück]