The First Book of the Sector
CHAPT. I. The Description, the Making, and the General Use of the SECTOR.
The Sector, in Geometry, is a Figure comprehended of two right Lines containing an Angle at the Center, and of the Circumference assumed by them. This Geometrical Instrument having two Legs, conteining all variety of Angles, and the distance of the Feet, representing the Subtenses of the Circumference, is therefore called by the same name.
It conteineth 12 several Lines or Scales, of which 7 are general, the other 5 more particular. The First is the Scale of Line, divided into 100 equal parts, and numered 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
The second is the Line of Superficies, divided into 100 unequal parts, and numered 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
3. The third, the Line of Solids, divided into 1000 unequal parts, and numered 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
4. The fourth, the Line of Sines and Chords, divided into 90 degrees, and numbered with 10, 20, 30 unto 90.
These four Lines, of Lines, of Superficies, of Solids, and of Sines, are all drawn from the Center of the Sector almost to the end of the Legs. They are drawn on both the Legs, that every Lines may heve ist fellow. All of them are of one Length, that they may answer one to the other: And every one hath his Parallels, that the eye may the better dinstinguish the Divisions. But of the Parallels those only which are inwardmost contein the true Divisions.
There are three other general Lines, which because they are infinite are placed on the Side of the Sector.
5. The first a Line of Tangents, numbered with 10, 20, 30, 40, 50, 60, signifying so many degrees from the beginning of the Line, of which 45 are equal to the whole Line of Sines, the rest follow as the length of the Sector,will bear.
6. The second, a Line of Secants, divided by Pricks into 60 degrees, is the same with that of the Line of Tangents to which it is joyned.
7. The third is the Meridian Line, or Line of Rumbs, divided unequal into degrees, of which the first 70 are almost equal to the whole Line of Sines, the rest follow unto 85, according to the length of the Sector.
Of the particular Lines inserted among the general, because there was void space.
8. The first are the Lines of Quadrature, placed between the Lines of Sines, and noted with 10, 9, 8, 7, S, 6, 5, 90, Q
9. The second, the Line of Segments, placed between the Lines of Sines and Superficies, divided into 50 parts, and numbered with 5, 6, 7, 8, 9, 10.
10. The third, the Lines of inscribed bodies in the same Sphere, placed between the Scales of Lines, and noted with D. S. I. C. O. T.
11. The fourth, the Line of Equated Bodies, placed between the Lines of Lines and Solids, and noted with D. I. C. S. O. T.
12. The fifth are the Lines of Metals, inserted with the Lines of Equated Bodies, (there beeing room suffcient), and noted with the characters (Alchemistische Symbole der Metalle).
There remain the Edges of the Sector, and on the one I have set a Line of Inches, which are the twelfe parts of a Foot Englisch: on the othe a lesser Line of Tangents to which the Gnomon is Radius.
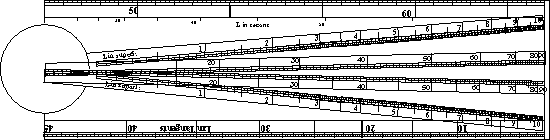
Der hier abgebildete Sector stammt aus eine Anzeige eines Instrumentenmachers an anderer Stelle des Buches. Gunters Werke haben keine Abbildungen eines Sectors.
2. Of the making of the Sector
Let a Ruler be first made either of Brass or of Wood unto the Figure before the Book annexed. Which may open and shut upon his Center: the Head of it may be about the twelfth part of the whole Length, that it may bear the movable Foot, and yet the most part of the Divisions may fall without it. Then let a movable Gnomon be set at the end of the movable Foot, and there turn upon an Axis, so as it may sometimes stand at a right Angle with the feet; and sometimes be inclosed within the Feet. But this is well known to the Work.man.
For drawing of the Lines. Upon the Center of the Sector, an Semidiameter somewhat shorter than one of the Feet, draw an occult Ark of a Circle, crossing the Closure of the inward Edge of the Sector, about the Letter T.
In this Ark, at one degree on either Side from the Edge, draw right Line from the Center, fitting them with Parallels, and divide them into an hundred equal parts, with Subdivisions into 2, 5, or 10, as the Line will bear, but let the Numbers set to them, be only 1, 2, 3, 4, etc. unto 10, as in the Example. These Lines so divided, I call the Lines or Scales of Lines; and they are the ground of all the rest.
In this Ark, at 5 degrees on either Side, from the Edge near T, draw other right Lines from the Center, and fit them with Parallels: these shall serve for the Lines of Solids.
Then on the other Side of the Sektor, in like manner, upon the Center, and equal Semidiameter, draw another like Ark of a Circle: and here again at one degree near on either Side from the Edge, near the letter Q, draw right Lines from the Center, and fit them with Parallels: These shall serve for the Lines of Sines.
At 5 degrees, on either Side from the Edge near Q, draw other right Lines from the Center, and fit them with Parallels: these shall serve for the Lines of Superficies.
These four principal Lines being drawn, and fitted with Parallels, we may draw other Lines in the middle between the Edges and the Lines of Lines, which shall serve for the Lines of Inscribed Bodies, and others between the Edges and the Lines of Quadrature. And so the rest as in the Example. These four principal Lines being drawn, and fitted with Parallels, we may draw other Lines in the middle between the Edges and the Lines of Lines, which shall serve for the Lines of Inscribed Bodies, and others between the Edges and the Lines of Quadrature. And so the rest as in the Example.
3. To divide the Lines of Superficies
Seeing the Superficies do hold in the Proportion of their homologal Sides duplicated by the 29. Pro. 6. Lib Euclid. If you shall find mean Proportionals between the whole Side, and each hundred part of the like Side, by the 13. Prop. 6. Lib. Euclid. All of them cutting the same Line, that Line so cut shall contain the Divisions required; wherefore upon the Center A, and Semidiameter equal to the Line of Lines, describe a Semicircle ACBD, with AB perpendicular to the Diameter CD. And let the Semidiameter AD be divided as the Line of Lines into an hundred parts, so shall the Divisions in AE be the Centers from whence you shall describe the Semicircles C19, C20, C30 etc- dividing the Line AB into an hundred unequal parts: and this Line AB so divided shall be the Line of Superficies, and must be transferred into the Sector. But let the numbers set to them be only I.1..2.3. unto 10, as in the example.
Or these Lines of Superficies may otherwise be transferred into the Sector, out of the Lines of Lines, by a Table of Square Roots; For the Root taken out of the Line of Lines, shall give the Square in the Lines of Superficies.
As, to inscribe the Division of 25 in the Lines of Superficies; put six Ciphers to 25, and make 25000000, then find the Square Root of this Number, which will be 5000.
Take therefore 5000 out of the Line of Lines (supposing the whole Line to be 10000) and it will give the true Distance between the Center, and the points of 25, in the Line of Superficies.
So, for the Division of 30,, put to 30 six Ciphers, and make it 30000000, whose Square Root is 5477. This (taken out of the Line of Lines) shall give the place for the Points of 30, in the Line of Superficies. And the like reason holdeth for all the rest, according to this following Table.
If any please to make use of a Diagonal Scale, equal to the Line of Lines, he may put eight Ciphers to the number proposed, and make the Table of Roots to five Places: So, his work will be more exact.
| A Table of Square Roots for the Division of the Lines of Superficies. | |||||||||||||
| Sq | Root | Sq | Root | Sq | Root | Sq | Root | Sq | Root | Sq | Root | Sq | Root |
| 0 | 15 | 3873 | 30 | 5477 | 45 | 6708 | 60 | 7746 | 75 | 8660 | 90 | 9487 | |
| 707 | 3937 | 5523 | 6745 | 7778 | 8689 | 9513 | |||||||
| 1 | 1000 | 16 | 4000 | 31 | 5568 | 46 | 6782 | 61 | 7810 | 76 | 8718 | 91 | 9539 |
| 1225 | 4062 | 5612 | 6819 | 7842 | 8746 | 9566 | |||||||
| 2 | 1414 | 17 | 4123 | 32 | 5657 | 47 | 6856 | 62 | 7874 | 77 | 8775 | 92 | 9592 |
| 1581 | 4183 | 5701 | 6892 | 7906 | 8803 | 9618 | |||||||
| 3 | 1732 | 18 | 4243 | 33 | 5745 | 48 | 6928 | 63 | 7937 | 78 | 8832 | 93 | 9644 |
| 1871 | 4301 | 5788 | 6964 | 7969 | 8860 | 9670 | |||||||
| 4 | 2000 | 19 | 4359 | 34 | 5831 | 49 | 7000 | 64 | 8000 | 79 | 8888 | 94 | 9695 |
| 2121 | 4416 | 5874 | 7036 | 8031 | 8916 | 9721 | |||||||
| 5 | 2236 | 20 | 4472 | 35 | 5916 | 50 | 7071 | 65 | 8062 | 80 | 8944 | 95 | 9747 |
| 2345 | 4528 | 5958 | 7106 | 8093 | 8972 | 9772 | |||||||
| 6 | 2449 | 21 | 4583 | 36 | 6000 | 51 | 7141 | 66 | 8124 | 81 | 9000 | 96 | 9798 |
| 2550 | 4637 | 6042 | 7176 | 8155 | 9028 | 9823 | |||||||
| 7 | 2646 | 22 | 4690 | 37 | 6083 | 52 | 7211 | 67 | 8185 | 82 | 9055 | 97 | 9849 |
| 2739 | 4743 | 6124 | 7246 | 8216 | 9083 | 9874 | |||||||
| 8 | 2828 | 23 | 4796 | 38 | 6164 | 53 | 7280 | 68 | 8246 | 83 | 9110 | 98 | 9899 |
| 2915 | 4848 | 6205 | 7314 | 8276 | 9138 | 9925 | |||||||
| 9 | 3000 | 24 | 4899 | 39 | 6245 | 54 | 7348 | 69 | 8307 | 84 | 9165 | 99 | 9950 |
| 3082 | 4950 | 6285 | 7382 | 8337 | 9192 | 9975 | |||||||
| 10 | 3162 | 25 | 5000 | 40 | 6325 | 55 | 7416 | 70 | 8367 | 85 | 9220 | 100 | 10000 |
| 3240 | 5050 | 6364 | 7450 | 8396 | 9247 | ||||||||
| 11 | 3317 | 26 | 5099 | 41 | 6403 | 56 | 7483 | 71 | 8426 | 86 | 9274 | ||
| 3391 | 5148 | 6442 | 7517 | 8456 | 9301 | ||||||||
| 12 | 3464 | 27 | 5196 | 42 | 6481 | 57 | 7550 | 72 | 8485 | 87 | 9327 | ||
| 3536 | 5244 | 6519 | 7583 | 8515 | 9354 | ||||||||
| 13 | 3606 | 28 | 5292 | 43 | 6557 | 58 | 7616 | 73 | 8544 | 88 | 9381 | ||
| 3674 | 5339 | 6595 | 7649 | 8573 | 9407 | ||||||||
| 14 | 3742 | 29 | 5385 | 44 | 6633 | 59 | 7681 | 74 | 8602 | 89 | 9434 | ||
| 3808 | 5431 | 6671 | 7714 | 8631 | 9460 | ||||||||
| 15 | 3873 | 30 | 5477 | 45 | 6708 | 60 | 7746 | 75 | 8660 | 90 | 9487 | ||
4. To divide the Lines of Solids.
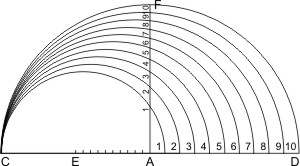
Seeing like Solids do hold the Proportion of their homologal Sides triglicated, if you shall find two mean Propotionals between the whole Side: all of them cutting the frame two right Lines, the former of those Lines so cut, shall contain the Division required.
Whereas upon the center A, and Semidiameter equal to the Line of Lines, describe a Circle and divide it into 4 equal parts C E B D, drawing the cross-Diameters C B E D. Then divide the semidiameter A C, first into 10 equal parts, and between the whole Line A D and A F, the tenth part of A C, seek out two mean Proportional Lines A I an A H: again between A C and AG (being two Tenth of A B) seek out two mean Proportional A L and A K, and so forward in the rest. So shall the Line A B, be divided into 10 unequal parts.
Secondly, divide each tenth part of the Line A C into 10 more, and between the whole Line AD, and each of them, seek out two mean Proportional as before: so shall the Line AB be divided now into an hundred unequal part.
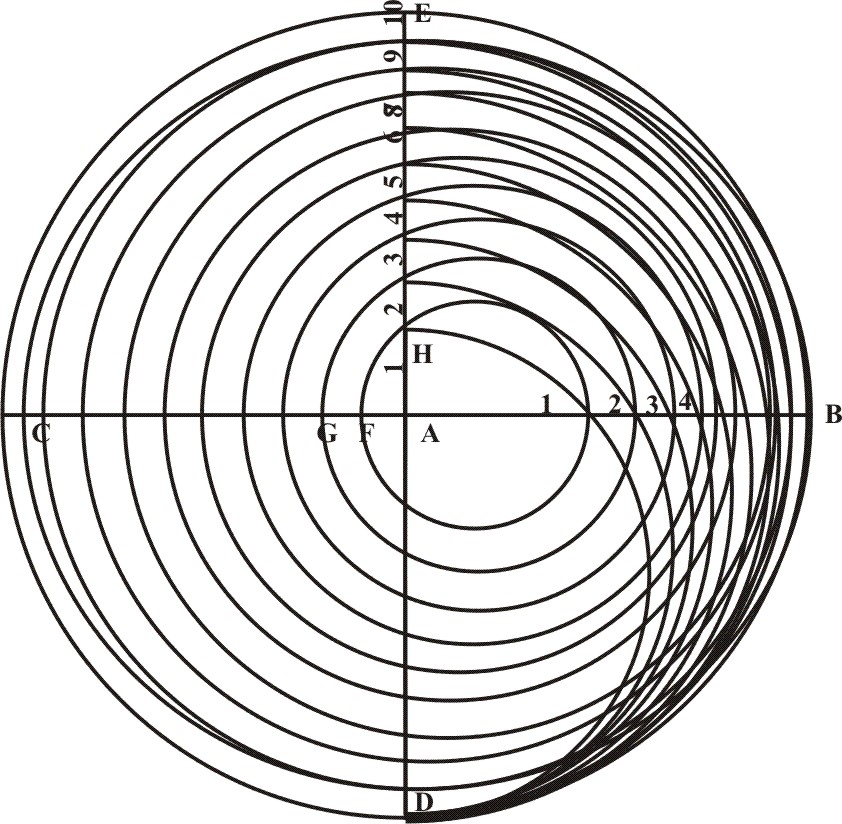
Thirdly,if the Length will bear it, subdivide the Line AC once again, each part in ten more, and between the whole Line AD, and each Subdivision, seek two mean Proportionals as before. So shall the Line A B be now divided into 1000 parts. But the Ruuler being short, it shall suffice, if those 10 which are nearest the Center be expressed, the rest be understood to be so divided, though actually they be divided into no more than 5 or 2, and this Line A B so divided shall be the Line of Solids, and must be transferred into the Sector: But let the Numbers set to them be only 1. 1. 1. 2. 3. etc. unto 10, as in the Example.
Or these Lines of Solids may otherweise be transferres into the Sector, out of the Line of Lines (or rather, out of a Diagonal Scale equal to the Line of Lines) by a Table of Cubic Roots. For the Root taken out the Line of Lines, shall give the Cube in the Line of Solids.
As to inscribe the Division of 125 in the Line of Solids; put xii. Ciphers to 125 , and make it 125000000000000: Then find the Cubic Root of the Number, which will be 50000- Take therefore 50000 out of the Line of Lines; (such as the whole Line is 100000) and it will give the true Distance between Points of 125 in the Line of Solids.
So, for the Division of 300, put 300 xii. Ciphers more, and make it 300000000000000, whose Cubic Root is 66943. This taken out of the Line of Lines, shall give the place for the points of 300 in the Line of Solids. And the like reason heldeth for all the rest, according to the ensuing Table.
| Cub | Root | Cub | Root | Cub | Root | Cub | Root | Cub | Root |
| 0 | 20 | 2714 | 50 | 3684 | 125 | 5000 | 275 | 6503 | |
| 0,5 | 794 | 21 | 2759 | 52 | 3733 | 130 | 5066 | 280 | 6542 |
| 1 | 1000 | 22 | 2802 | 54 | 3780 | 135 | 5130 | 285 | 6581 |
| 1,5 | 1145 | 23 | 2844 | 56 | 3826 | 140 | 5192 | 290 | 6619 |
| 2 | 1260 | 24 | 2884 | 58 | 3871 | 145 | 5254 | 295 | 6657 |
| 2,5 | 1357 | 25 | 2924 | 60 | 3915 | 150 | 5313 | 300 | 6694 |
| 3 | 1442 | 26 | 2962 | 62 | 3958 | 155 | 5372 | 305 | 6731 |
| 3,5 | 1518 | 27 | 3000 | 64 | 4000 | 160 | 5429 | 310 | 6768 |
| 4 | 1587 | 28 | 3037 | 66 | 4041 | 165 | 5485 | 315 | 6804 |
| 4,5 | 1651 | 29 | 3072 | 68 | 4082 | 170 | 5540 | 320 | 6840 |
| 5 | 1710 | 30 | 3107 | 70 | 4121 | 175 | 5593 | 325 | 6875 |
| 5,5 | 1765 | 31 | 3141 | 72 | 4160 | 180 | 5646 | 330 | 6910 |
| 6 | 1817 | 32 | 3175 | 74 | 4198 | 185 | 5698 | 335 | 6945 |
| 6,5 | 1866 | 33 | 3208 | 76 | 4236 | 190 | 5749 | 340 | 6980 |
| 7 | 1913 | 34 | 3240 | 78 | 4273 | 195 | 5799 | 345 | 7014 |
| 7,5 | 1957 | 35 | 3271 | 80 | 4309 | 200 | 5848 | 350 | 7047 |
| 8 | 2000 | 36 | 3302 | 82 | 4344 | 205 | 5896 | 355 | 7081 |
| 8,5 | 2041 | 37 | 3332 | 84 | 4380 | 210 | 5944 | 360 | 7114 |
| 9 | 2080 | 38 | 3362 | 86 | 4414 | 215 | 5991 | 365 | 7147 |
| 9,5 | 2118 | 39 | 3391 | 88 | 4448 | 220 | 6037 | 370 | 7179 |
| 10 | 2154 | 40 | 3420 | 90 | 4481 | 225 | 6082 | 375 | 7211 |
| 11 | 2224 | 41 | 3448 | 92 | 4514 | 230 | 6127 | 380 | 7243 |
| 12 | 2289 | 42 | 3476 | 94 | 4547 | 235 | 6171 | 385 | 7275 |
| 13 | 2351 | 43 | 3503 | 96 | 4579 | 240 | 6214 | 390 | 7306 |
| 14 | 2410 | 44 | 3530 | 98 | 4610 | 245 | 6257 | 395 | 7337 |
| 15 | 2466 | 45 | 3557 | 100 | 4642 | 250 | 6300 | 400 | 7368 |
| 16 | 2520 | 46 | 3583 | 105 | 4718 | 255 | 6341 | 405 | 7399 |
| 17 | 2571 | 47 | 3609 | 110 | 4791 | 260 | 6383 | 410 | 7429 |
| 18 | 2621 | 48 | 3634 | 115 | 4863 | 265 | 6423 | 415 | 7459 |
| 19 | 2668 | 49 | 3659 | 120 | 4932 | 270 | 6463 | 420 | 7489 |
| 20 | 2714 | 50 | 3684 | 125 | 5000 | 275 | 6503 | 425 | 7518 |
| Cub | Root | Cub | Root | Cub | Root | Cub | Root | ||
| 425 | 7518 | 575 | 8316 | 725 | 8984 | 875 | 9565 | ||
| 430 | 7548 | 580 | 8340 | 730 | 9004 | 880 | 9583 | ||
| 435 | 7577 | 585 | 8363 | 735 | 9025 | 885 | 9601 | ||
| 440 | 7606 | 590 | 8387 | 740 | 9045 | 890 | 9619 | ||
| 445 | 7635 | 595 | 8411 | 745 | 9065 | 895 | 9637 | ||
| 450 | 7663 | 600 | 8434 | 750 | 9086 | 900 | 9655 | ||
| 455 | 7691 | 605 | 8458 | 755 | 9106 | 905 | 9673 | ||
| 460 | 7719 | 610 | 8481 | 760 | 9126 | 910 | 9691 | ||
| 465 | 7747 | 615 | 8504 | 765 | 9146 | 915 | 9708 | ||
| 470 | 7775 | 620 | 8527 | 770 | 9166 | 920 | 9726 | ||
| 475 | 7802 | 625 | 8550 | 775 | 9185 | 925 | 9743 | ||
| 480 | 7830 | 630 | 8573 | 780 | 9205 | 930 | 9761 | ||
| 485 | 7857 | 635 | 8595 | 785 | 9225 | 935 | 9778 | ||
| 490 | 7884 | 640 | 8618 | 790 | 9244 | 940 | 9796 | ||
| 495 | 7910 | 645 | 8640 | 795 | 9264 | 945 | 9813 | ||
| 500 | 7937 | 650 | 8662 | 800 | 9283 | 950 | 9830 | ||
| 505 | 7963 | 655 | 8685 | 805 | 9302 | 955 | 9848 | ||
| 510 | 7990 | 660 | 8707 | 810 | 9322 | 960 | 9865 | ||
| 515 | 8016 | 665 | 8729 | 815 | 9341 | 965 | 9882 | ||
| 520 | 8041 | 670 | 8750 | 820 | 9360 | 970 | 9899 | ||
| 525 | 8067 | 675 | 8772 | 825 | 9379 | 975 | 9916 | ||
| 530 | 8093 | 680 | 8794 | 830 | 9398 | 980 | 9933 | ||
| 535 | 8118 | 685 | 8815 | 835 | 9417 | 985 | 9950 | ||
| 540 | 8143 | 690 | 8837 | 840 | 9435 | 990 | 9967 | ||
| 545 | 8168 | 695 | 8858 | 845 | 9454 | 995 | 9983 | ||
| 550 | 8193 | 700 | 8879 | 850 | 9473 | 1000 | 10000 | ||
| 555 | 8218 | 705 | 8900 | 855 | 9491 | ||||
| 560 | 8243 | 710 | 8921 | 860 | 9510 | ||||
| 565 | 8267 | 715 | 8942 | 865 | 9528 | ||||
| 570 | 8291 | 720 | 8963 | 870 | 9546 | ||||
| 575 | 8316 | 725 | 8984 | 875 | 9565 | ||||
5. To divide the Line of Sines and Tangents on the Side of the Sector
Upon the Center A, and the Semidiameter equal to the Line of Lines, describe a Semicircle ABCD with AB, perpendicular to the Diameter CD. Then Divide the Quadrant CB, BD, each of them into 90, and subdivide each degree into two part: For so if straight Lines be drawn parallel to the Diameter CD, through these 90 and their Subdivisions, they shall divide the Perpendicular AB unequally into 90.
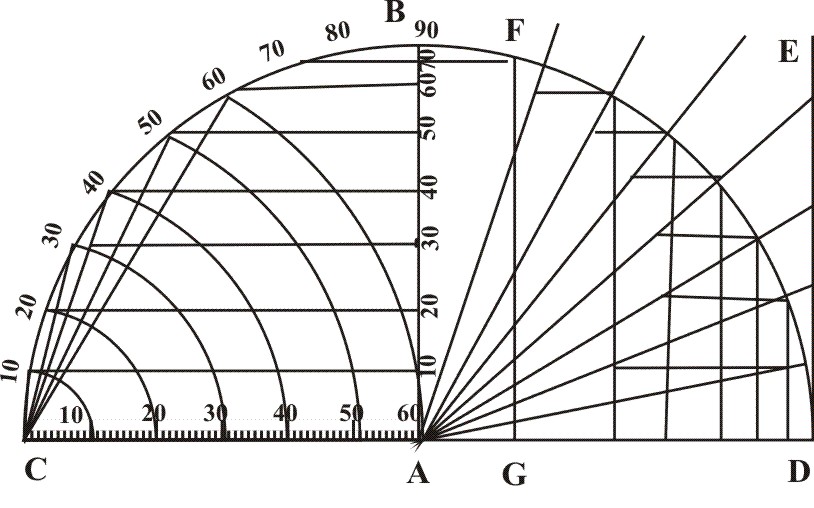
And this AB (so divided) shall be the Line of Sines, and must be transferred into the Sector. The Number set to them are 10, 20, 30, &c. unto 90, as in the Example.
If now in the point D, unto the Diameter CD, we shall raise a Perpendicular DE, and to it draw straight Lines from the Center A, through each Degree of the Quadrant DB, these straight Lines shall be Secants, and this Perpendicular so divided shall be the Line of Tangents, and must be transferred unto the Side of the Sector. The Numbers set to them, are to be 10, 20, 30, &c. as in the Example.
If between A and D, another straight Line GF be drawn parallel to DE, it will be divided by those Lines from the Center like sort as DE is divided, and it may serve for the lesser Line of Tangents, to be set on the Edge of the Sector.
If the Compasses shall be extended from C to each degree of the Quadrant CB, and those Extents transferred into one Line (CA) this Line CA so divided into 60 (or rather into 90 gr.) shall be a Line of Chords, and may be set on some void place of the Sector.
These Lines of Sines and Tangents, may yet otherwise be transferred into the Sector out of the Line of Lines (or rather out of a Diagonal Scale equal to the Line of Lines) by Tables of Natural Sines and Tangents.
For the Sine of 90 gr. Being equal 1 the whole Line of Lines of 100000 parts, the Sine of 30 gr. Will be equal 50000 (half the Line of Lines;) and the Sine of 45 gr. Equal to 70710 parts of the Line of Lines, according to the usual Table of natural Sines.
In like manner the Tangent of 45 gr. Being equal to the whole Line of Lines, the Tangent of 40 gr. Will be equal to 81910 parts of the Line of Lines, the Tangent of 50 gr. Equal to 119175, that is to one Radius (or whole Line) and 19175 parts more of the Line of Lines according to the old Table of Tangents.
And (upon the same ground) the Secant of 40 gr. Will be equal to 1.30540, that is one Radius and 30540 parts of the Line of Lines; and the Secant of 50 gr. Equal to 1.55572, and so the rest, according to the like Table of Secants.
The Line of Chords may also be divided by help of the Table of Sines and the Line of Lines. For the double Sine of half the Ark taken out of the Line of Lines will give the Chord.
As if the Ark proposed were 60 gr. The half of this Ark is 30 gr. And the Sine thereof 50000, which being doubled, make 100000, the whole Line of Lines, equal to a Chord of 60 gr.
So for the Chord of 90 gr. The half Ark ist 45 degrees, and the Sine thereof 70710, which being doubled, make 1414140, that is, one Radius, and 41410 parts of the Line of Lines, equal to the Cord of 90 gr. Required.
6. To show the Ground of the Sector.
Let AB, AC, represent the Legs of the Sector; then seeing these two AB, AC are equal, and their Sections AD, AE, also equal, they shall be cut proportionally: and if we draw the Lines BC, DE, they will be parallel by Prop. 2. Lib. 6. of Euclid, and so the Triangles ABC, ADE, shall be equianled, by reason of the common Angle at A, and the equal Angles at the Base, and therefore shall have the Sides proportional about those Angles, by Prop. 4. Lib. 6. of Euclid.
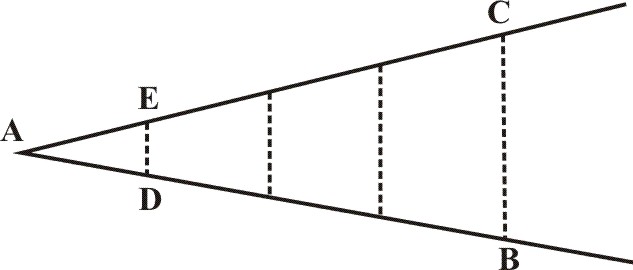
The Side AD shall be to the Side AB, as the Basis, DE, unto the parallel Basis BC, and by conversion AB shall be unto AD, as BC unto DE; and by permutaion AD shall be untoDE, as AB to BC &c. So that if AD be the fourth part of the Side AB, then DE shall also be the fourth part of his parallel Basis BC. The like reason holdeth in all other Sections.
7. To show the general Use of the Sector.
There may some Conclusions be wrought by the Sector even then when it is shut, by reason that the Lines are all of one length: but generally the Use hereof consists in the solution of the Golden Rule, where three Lines being given of a known Denomination, a fourth Proportional is to be found. And this Solution is diverse in regard both of the Lines and of the Entrance into the Work.
The Solutions in regard of the Lines is sometimes simple, as when the Work begun and ended upon the same Lines. Sometimes it is compound, as when it is begun on one kind of Lines and ended on another. It may be begun upon the Line of Lines, and finished upon the Lines of Superficies. It may begin on the Sines, and end on the Tangents.
The Solution in regard of the Entrance into the work, may be either with a Parallel, or else Lateral on the Side of the Sector, I call it Parallel Entrance, or entring with a Parallel, when the two Lines of the first Denomination are applied in the parallels, and the third Line, and that which is fought for, are on the side of the Sector: I call it lateral Entrance, or entring on the side of the Sector, when the two Lines of the first Denomination are on the side of the Sector, and the third Line, and that which is to be found out do stand in the Parallels.
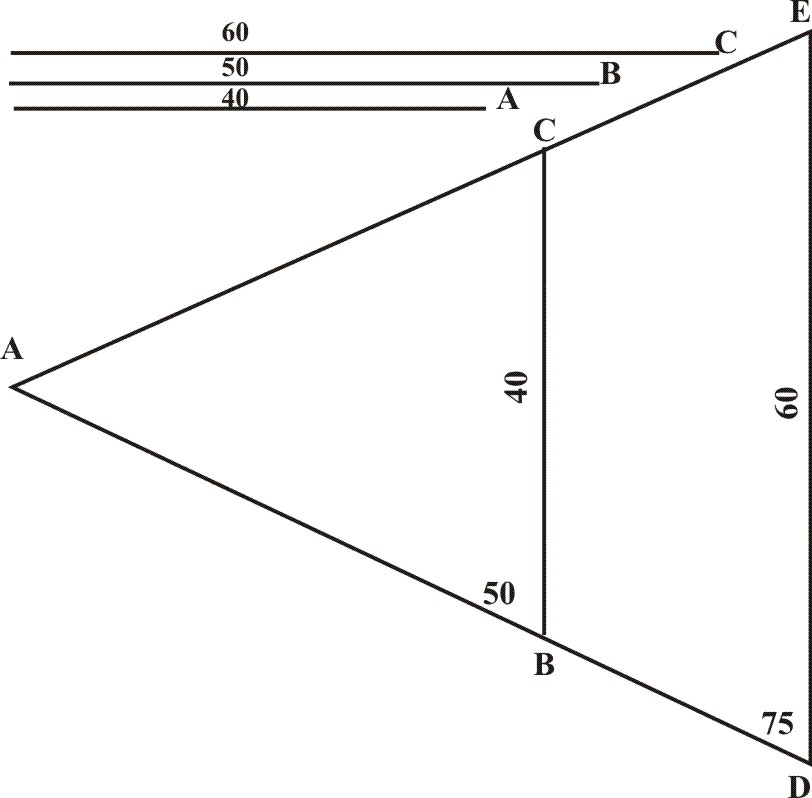
As for Example, let there be given three Lines, A, B, C, to which I am to find a fourth Proportional, let A mesasured in the Line of Lines, be 40, B 50, C 60, and suppose the Question be this: If 40 Months give 50 pounds, what shall 60? Here are Lines of two Denominations, one of Months, another of Pounds, and the first, with which I am to enter, must be that of 40 Months. If then I would enter with a Parallel, first I take A, the Line of 40, and put it over as a Parallel in 50, reckoned in the Line of Lines, on either side of the sector from the Center, so as it may be the Base of an Isoscheles Triangle BAC, whose Sides AB, AC are equal to B, the Line of the second Denomination.
Then the Sector being thus opened, I take C the Line of 60, between the Feet of the Compasses, and carrying them parallel to BC, I find then to cross the Lines AB, AC, on the side of the Sector in D and E, numbered 75, wherefore I conclude the Line AD or AE ist the fourth Proportional and the correspondent Number 75, which was required.
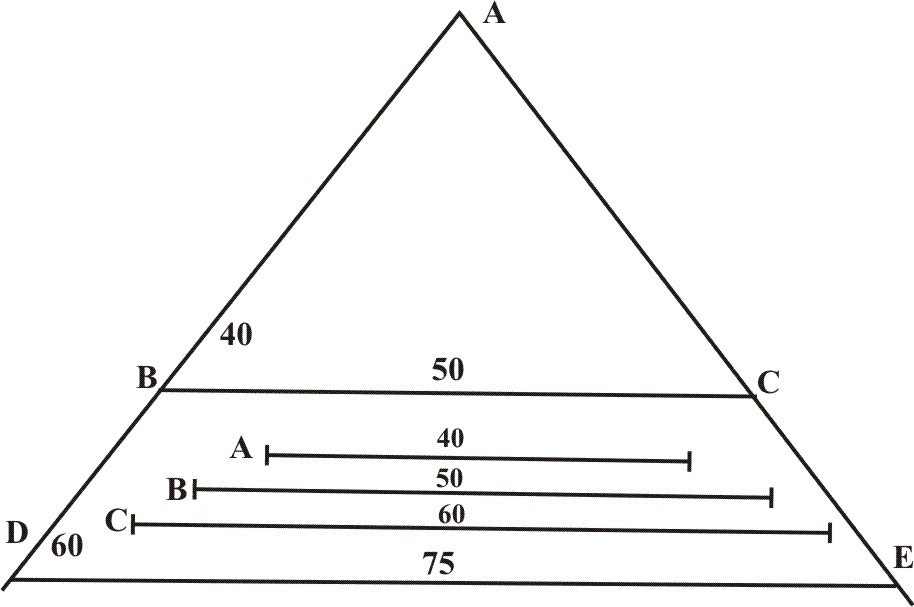
But if I would enter on the Siede of the Sector, then would I dispose the Lines of first Denomination A and C in the Line of Lines, on both sides of the Sector in AB, AC, and in AD, AD, so as they should all meet in the Center A, and then taking B the Line of the second Denomination, put it over as a Parallel in BC, that it may be the Basis of the Isoscheles Triangle BAC (whose Sides AB, AC, are equal to A the first Line of the first Denomination) for so the Sectoer being just opened, the other Parallel from D to E, shall be the fourth Proportional which was required, and if it be measured with other Lines, it shall be 75, as before.
In both these manners of Operations, the two first Lines do serve to open the Sector to his due Angele, the Difference between them especially this, that in Paralle Entrance, the two Lines of first Denomination, are placed in the Parallels BC, DE, and in Lateral Entrance they are placed on both Sides of the Sector, in AB, AD, and in AC, AE.
Now in simple solution which is begun and ended upon the same kind of Lines, it is all one which of the two latter Lines be put in the second or third place. As in our Example we may say, As 40 are to 50, so 60 unto 75, or else, As 40 are to 60, so 50 unto 75. And hence it cometh, that we may enter both with a Parallel, and on the Sides two manner of ways at either Entrance, and so the most part of Questions may be wrought four several ways, though in the Propositions following, I mention only that which is most convenient. If any have not the Sector, he may make use of the former Figure, as in our Example, where we have three Numbers given (40.50.60) to find the fourth Proportional.
First, edraw a right line (AD) to represent one of the Lines of the Sectror. Then take out the first Number (48) out of the Line of Lines, and priek it down from A to B; and on the Center (A,) and Semidiameter (AB) describe an occult Ark of a Circle from B towards C. In like manner, take out (60) the other Number of the first Denomination, and prick it down from A to D. And on the Center (A) and Semidiameter (AD) describe a second Ark of a Circle, from D toward E. That done, take the third Number (50) and inscribe it into the first Ark from B to C; and laying the Ruler to the Center (A) and the Point C, draw a right Line AC, out in length, till it cut the second Ark in the point E. So the Distance from D to E (taken and measured in the same Scale with the thrid Number) will give 75 for the fourth Proportional.
Thus much for the general Use of the Sector, which being considered, and well understood, there ist nothing hard in that which followeth.