The First Book of the Sector
CHAP. II The Use of the Scale of Lines.
1. To set down a Line, resembling any given Parts or Fraction of Parts.
The Lines of Lines are divided actually into 100 parts, but we have put only 10 Numbers on them. These we would have to signifie either themselves alone, or ten times themselves, or an hundred times themselves, or a thousans times themselves,as the matter shall require. As if the Numbers given be no more than 10, then we may think the Lines only divided into ten parts according to the number set to them. If they be more than 10, and not more than 100, then either Line shall contain 100 parts, and the Numbers set to them shal be the value 10, 20, 39, &c. as they are divided actually. If yet they be more than 100, then every part must be thought to be divided into 10, and either Line shall be 1000 parts, and the Numbers set to them shall be in value 100, 200, 300, and so forward still increasing themselves by 10. This being presupposed, we may number the Parts and Fractions of Parts given in the Line of Lines; and taking out the Distance with a pair of Compasses, set it by, for the Line so taken shall resemble the Number given.
In this manner may we set down a Line resembling 75, if either we take 75 out of the hundred parts, into which one of the Line of Lines is actually divided, and note it in A, or 71/2 of the first 10 parts, and note it in B, or only ¼ of one of those hundred Parts, and note it in C. Or if this be either too great or too small, we may a Scaleat pleasure, by opening the Compass to some small distance, and running it ten times over, then opening the Compass to these ten, run them over nine times more, and set Figures to them as in the Example, and out of this we may take what parts we will as before.
To this end I have divided the Line of Inches on the Edge of the Sector, so as one Inche conteineth 8 parts, another 9, another 10, &c. according as they are figured, and as they are distant from the other end of the Sector, that so we might have a better Estimate.
2. To increase a Line in a given Proportion.
3. To diminish a Line in a given Proportion.
Take the Line given with a pair of Compaases, and oprn the Sector, so as the Feet of the Compasses may stand in the point of the Number given, then keeping the Sector at this Angle, the Parallel Distance of the points of the Number requires, shall give the Line required.
Let A be a Line given to be increased in the Proportion of 3 to 5. First, I take the Line A with the Compasses, and open the Sector till I may put it over in the Points of 3 and 3, so the Parallel between the Points of 5 and 5, doth give me the Line B, which was required.
In like manner, if B be a Line given to be diminished in Proportion of 5 to 3, I take the Line B: and to it open the Sectroe in the Points of 5 and 5, so the Parallel between the Points of 3 and 3, doth give me the Line A, which was required.
If this manner of work doth not suffice, we may multiply or divide the Numbers given by 2, or 3, or 4, &c. And so word by their Numbers equi-multiplices, as for 3 and 5, we may open the Sector in 6 and 10, or else in 9 and 15, or else in 12 and 20, or in 15 and 25, or in 18 and 30, &c.
4. To divide a Line into any number of Parts given.
Take the Line given, and open the Sector according to the length of the said Line in the points of the parts, whereinto the Line should be divided, then keeping the Sector at this Abgle, the Parallel Distance between the points of I and I shall divide the Line given into the Parts required.
Let AB be the Line given, to be divided into five parts, first I take this Line AB, and to it open the Sector in the points 5 an 5, the Parallel between the points 1 and 1, doth give me the Line AC, which doth divide it into the parts required.
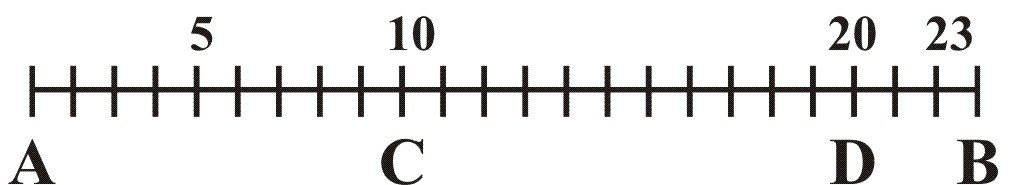
Or let the like Line AB be to be divided into 23 parts. First, I take out the Line and put it upon the Sectroe in the points of 23, then may I by the former Proposition diminish it in AC, CD, in the Proportion of 23 to 10, and after that divide the Line AC into 10, &c. as before.
5. To find a Proportion between two or more right Lines given.
Take the greater Line given, and according to it open the Sector in the points of 100 and 100, then take the lesser Lines severally, and carry them parallel to the greater, till they stay in like points, so the Number of points wherein they stay, shall shew their Proportion unto 100.
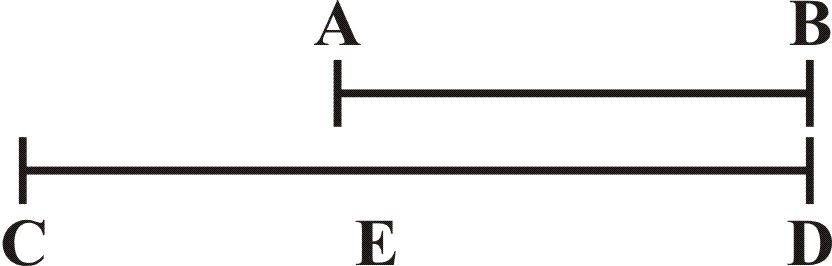
Let the Lines given be AB, CD, first I take the Line CD, and to it open the Sector in the points 100 and 100, then keeping the Sector at this Angel, I enter the lesser Line AB, parallel to the fomer, and find it to cross the Lines of Lines in the points of 60. Wherefore the Proportion of AB to CD, is as 60 to 100.
Or if the Line CD be greater than can be put over the Points of 100, then I admit the lesser Line AB to be 100, and cutting off CE equal to AB, I find the Proportion of CE unto ED to be as 100, almost to 67; wherefore this way the Proportion of AB unto CD, is as 100 unto almost 167.
This Proportion may also not unfitly be wrought by any other Nuimber, that admits several Divisions, and namely, by the Numer of 60.
And so the lesser Line will be found to be 36, which is as before in lesser Numbers, as 3 unto 5. It may also be wrought without opening the Sector. For if the Lines between which we seek a proportion, be applied to the Line of Lines (or any other Sclae of equal parts) there will be such Proportuions found between them, as between the Lines to which they are equal.
6. The Lines being given, to find a third in continual Proportion.
First place both the Lines given, on both sides of the sector from the Center, and mark the terms of their Extension, then take out the second Line again, and to it open the Sector, in the terms of the first Line, so keeping the sectoer at this Angle, the parallel Distance between the terms of the second Line, shall be the third Proportion.
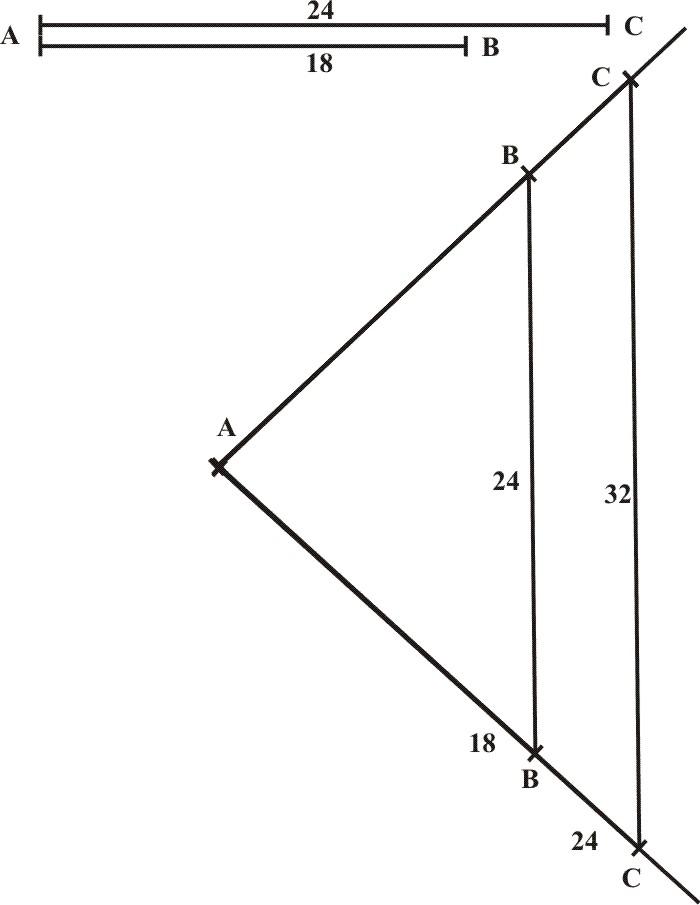
Let the two Line give, AB, AC, which I take out and place on both sides of the Sector, so as they all meet in the Center A, let the terms of the first Line be B and B, the terms of the second C and C. Then do I take out AC the second Line again, and to it open the Sector in the terms BB. So the Parallel between C and C doth give me the third Line in continual Proportion. For as AB is unto AC, so BB equal to AC, is unto CC.
7. Three Lines being given, to find the fourth in dissentinual Proportion.
Here the first Line and the third are to be placed on both sides of the Sector from the Center, then take out the second Line, and to it open the Sector in the terms of the first Line. For keeping the Sector at this Angle, the parallel Distance between the terms of the third Line, shall be the fourth Proportional. Let the three Lines be A, B, C.
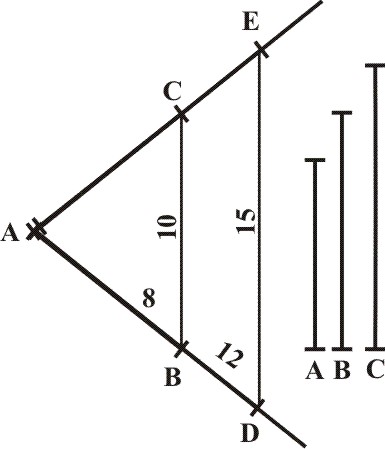
First, I take out A and C, and place them on both sides of the Sector, in AB, AC, and AD, AE, laying the beginning of both Lines at the Center A, then do I take out B the second Line, according to it I open the Sector in B and C, the terms of the first Line: so the Parallel between D and E, doth give me the fourth Proportional which was required.
As in Arithmetick, it suffices if the first and third Number given be of the Denomination, the second and the fourth which is required be of another. For one and the same Denomination is not required necessarily in them all. So in geometry, it sufficeth if the Sides AB, AD, resembling the first and third Lines given be measured in one Scale, and the Parallels BC, DE be measured in another, Wherefore knowing the Proportion of A the first Line, and C the third Line by the fifth Proposition before. Which is here as 8 to 12, and descending in lesser Numbers, as 16 unto 24, or 18 to 27, or 20 to 30, or 30 to 45, or 40 to 60, &c. If the Sector be opened in the points 0f 8 and 8, to the quantity of B, the second Line given, then a Prallel between 12 and 12, shall give DE, the fourth Line required. So likewise if it be opened in 4 and 4, then a Parallel between 6 and 6; or if in 16 and 16, then a Parallel between 24 and 24 shall give the same DE: and so to the rest.
8. To divide a Line in such sort as another Line is before divided.
First, take out the Line given, which is already divided, and laying it on both sides of the Sector from the Center; mark how far it extendeth. Then take out the second Line which is to be divided, and to it open the sector in the terms of the first Line. This done, take out the parts of the first Line, and place them also on the same side of the Sector from the Center. For the Parallells taken in the terms of these parts shall be the correspondent parts in the Line which is to be divided.
Let AB, be the Line divided in D and E, and BC the Line which I am to divide in such sort, as AB is divided.
First I take the Line AB, and place it on the Line of Lines in AB, AC, both from the Center A, then take I out the second BC, and to it open the Sector in B and C, the terms of the first Line. The Sector thus opened to his due Angle, I make out AD and AE, the parts of the first Line AB, and place them also on both sides of the Sector AD, AE, so the Parallel DD giveth me BF, and the Parallel EE giveth BG, and the Line BC is divided in F and G, as the other Line AB in D and E, which was required.
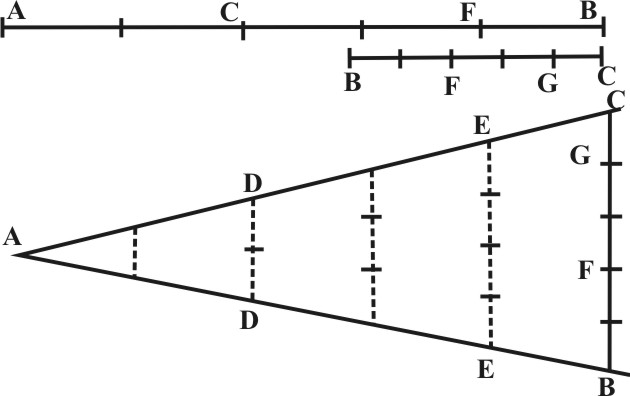
If the Line AB were longer than one of the Sides of the Ruler, then should I find what proportion it hath to his parts AD, AE, and that known, I may work as before in the former Proposition.
9. Two Numbers being given, to find a third in continual Proportion.
First reckon the two numbers given on both sides of the Lines of Lines from the Center, and mark the terms to which either of them extendeth, then take out a Line resembling the second number again, and to it open the Sector in the terms if the first number, for so keeping the Sector at this Angle, the Parallel Distance between the terms of the second lateral Number, being measured in the same Scale, from whence his Parallel was taken, shall give the third Number Proportional.
Let the two Numbers given be 18, 24. These being resembled in Lines, the work will be in amanner all one that in Prop. 6. and so the third Proportional number will be found to be 32.
10. Three Numbers being given, to find a fourth in discontinual Proportion.
The Solution of this Proposition, is in a manner all one with that before in Prop. 7: only there may be some difficulty in placing of the numbers. To avoid this, we must remember that three numbers being given, the question is annexed but to one, and this must always be placed in the third place, that which agrees with the third number in denomination, shall be the first number, and that which remaineth the second number. This being considered, reckon the first and third numbers, which are of the first Denomination on both sides of the Lines of Lines from the Center, and mark the terms to which either extendeth, then take out a Line resembling the second number, and to it open the Sector at this Angle, the parallel Distance between the terms of the third lateral Number, being measured in the same Scle from whence his Parallel was taken, shall give the fourth number Proportional.
As if a question were proposed in this manner, 10 yards cost 8 £ how many yards may we buy for 12 £ here the question is annexed to 12; and therefore it shall be the first number, and because 8 is the same denomination, it shall be the first number, then 10 remaining, it must be the second number, so will they stand in this order, 8, 10, 12. These being resembled in Lines, the work will be in a manner the same with tat in Prop. 7. and the fourth Proportional number will be found to be 15: for as 8 are to 10, so 12 unto 15.
And this holdeth in direct Proportion; where as the first number is the second, so the third to the fourth. So that if the third number be greater than the first, the fourt will be greater than the second; or if the third number be less than the first, the fourth will be less than the second, but in reciprocal Proportion, commonly called the Back Rule, where, by how much the first number is greater than the third, so much the second will be less than the fourth, or by how much the first number is less than the third, so much the second will be greater than the fourth; the manner of working must be contrary, that is, the sector is to be opened in terms of the third number: and the Parallel resembling the number required, is to be found between the terms of the nurst number, the rest may be observed as before, as for example.
If twelve men would raise a Frame in ten days, in how many days would eight men raise the same Frame? Here, because the fewer men would require longer time, though the numbers be 12, 10, 8, yet the fourth Proportional will be found to be 15.
So if 60 Yards of three quarters of a Yard in bredth would hang round a room, and it were required to know how many Yards of half a Yard in bredth would serve for the same room. The fourth Proportional would be found to be 90.
So if to make a Foot superficial 12 inches in bredth do require 12 inches in length, and the bredth being 16 inches, it were required to know the length. Here, because the more bredth, the less length, the fourth proportional will be found to be 9.
So if to make a solid Foot, a Base of 144 inches, require 12 inches in height, and a Base given being 216 inches, it were required to know how many inches it shall have in height. The fourth Proportional would be found to be 8.
This last Proposition of finding a fourth Proportional Number may be wrought also by the Lines of Superficies, and by the Lines of Solids.