The First Book of the Sector

Chap. IV The Use of the Lines of Solids.

1. To find a Proportion between two or more like Solids.

In the Sphere, in regular, parallel, and other like bodoies, whose Sides next the equal Angles are proportional, the work is in amanner the same, with that in the first Proposition of Superficies, but that is wrought on other Lines.

Take one of the sides of the greater Solid, and according to it open the Sector in the points 1000 and 1000, in the Lines of Solids, then take the like Sides of the lesser Solids severally, and carry them parallel to the former, till they stay in like points, so the number of points wherein they stay shall shew their proportion to 1000.

Let A and B be the like Sides of like Solids, either the Diameters or Semidimeters of two Speres, or the sides of two Cubes or other like. First I take the side A, and to it opne the Sector in the points of 1000, then keeping the Sector at this Angle, I enter the lesser Side B parallel to the former, and find it to cross the Line of Solids in the points of 400, and such ist the Proportion between the Solids required, which in lesser Numbers is, as 5 to 2.

This proposition might have been wrought by 60, or any other Number that admits several Divisions.

It may also be wrought without opening the Sector, for if the sides of the Solids given be applied to the Lines of Solids, beginning always at the Center of the Sector, there will be such Proportion between them, as between the Numbers of parts whereon they fall.

2. To augment a Solid in a given proportion.

3. To diminish a Solid in a given proportion.

Take the side of the Solid given, and to it open the Sector, in the points of the Number given: then keeping the Sector at that Angle, the parallel Distance between the points of the Number required, shall give the like Side of the Solid required.

If it be a parallelopipedon, or some irregular Solid, the other like Sides may be found out in the same manner, and with them the Solids required, may be made up with the same Angles.

Let A be the side of a Cube, to be augmented in the Proportion of 2 to 3. First, I take the side A, and put it over in the Lines of solids in 2 and 2, so the parallel between 3 and 3, doth give me the side B, on which if I make a Cube, it will have such Proportion to the Cube of A, as 3 to 2.

In like manner, if B were the Diameter of a Sphere, to be diminished in the proportion of 3 to 2. I would take out B, and put it over in the Lines of Solids, in 3 and 3, so the Parallel between 2 and 2, would give me A: to which Diameter if I should make a Sphere, it would be less than the Sphere, whose Diameter is B, in such a proportion as 2 is less than 3.

Here also for variety of work, may the like caution be observed to that which we gave in the third Proposition of Lines.

4. To add one like Solid to another.

5. To subtract one like Solid from another.

First the Proportion between the sides of the like Solids given, is to be found by the first Proposition of Solids: then add or subtract those Proportions, and accordingly augment or diminish by the former Proposition.

As if A and B were the sides of two Cubes, and it were required to make a third Cube equal to them both: first the Proportion between the sides A and B, would be found to be as 100 to 40, or in lesser terms as 5 to 2: then because 5 and 2 being added do make 7, I augment the side A, in the proportion of 5 to 7, and produce the side C, on which if I make a Cube, it will be equal to both the Cubes of A and B, which was required.

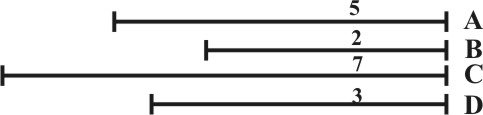
In like manner A and B being the sides of two Cubes, if it were required to substract the Cube of B out of the Cube of A, and to make a Cube equal to the Remainder. Here the Proportion being as 5 to 2, because 2 taken out of 5, the Remainder is 3, I should diminish the side A in the proportion of 5 to 2, and so I should have the side D, on which if I make a Cube, it will be equal to the Remainder, when the Cube of B is taken out of the Cube of A, that is, the two Cubes made upon B and D shall be equal to the first Cube made upon the side A.

6. To find two mean proportional Lines between two extreme Lines given.

First I find what Proportion is between the two extreme Lines given, as they are Lines, by the fifth Proposition of Lines, then open the Sectror in the Lines of Solids, to the quantity of the former Extreme, and a Parallel between the points of the number belonging to the other Extreme, shall be that mean Proportional, which is next the former Extreme. This done, open the Sectoer again to this mean proportional in the points of the fromer Exterem, and the parallel Distance between the points of the latter Extreme, shall be the other mean proportional required.

Let the two extreme Lines given be A and D, the Proportion between them, as they are Lines, will be found to be 27 to 8. Wherefore I take the Line A, and put it over in the Lines of Solids between 27 and 27, and keeping the Sector at this Angle, his Parallel between 8 and 8 doth give me B the mean Proportional next unto A. Then put I over this Line B, between the aforesaid 27 and 27, and this Parallel between 8 and 8 doth give me the Line C, the other mean Proportional which was required.

Again, for proof of the operation I put over this Line C in the aforesaid 27 and 27, and his Parallel between 8 nad 8 doth give me the very Line D: whereby it is plain that the four Lines do hold in continual Proportion; and so B and C are found to be Mean Proportionals between A and D the Extreme given.

7. To find two mean proportional Numbers between two extreme Numbers given.

First reckon the Numbers given on both sides of the Line of Solids, beginning from the Center, and marking the terms whereto they extend: then take a Line out of the Line of Lines, or any other Scale of equal parts resembling the former of those Numbers, and put it over in the Line of Solids, between the points of his like Number, and a Parallel between the points belonging to the other Extreme, measured in the Scale from whence the other Parallel was taken, shall give that mean proportional Number which is next the former Extreme. This done open the Sector again to this mean Proportional in the Points of the former Extreme, and the parallel Distance between the points of the latter Extreme, measured in the same Scale as before, shall there shew the other mean Proportional required.

Let the two extreme Numbers given be 27 and 8, if I shall take the Line A, resembling 27 in a Scale of equal parts, and to it open the Sector in 27 and 27, in the Line of Solids, his Parallel between 8 and 8 doth give me B, for his next mean Proportional, and this measured in the former Scale doth extend to 18. Then put I over this Line B, between the foresaid 27 and 27, and his Parallel between 8 and 8 doth give me C, for the other mean Proportional, and this measured in the former Scale doth extend to 12. Again, for proof of my work, I put over this Line C, between 27 and 27, as before, and his Parallel between 8 and 8 doth give me D, which measured in the former Scale doth extend to 8, which was the latter extreme Numeber given; whereby it is plain, that these four Numbers do hold in continual Propotion: and therefore 18 and 12 are Mean Proportionals between 27 and 8, which was required.

If you suppose Pricks under the Number given as in Arithmetical Extractiuon, and that last Prick to the left hand shall fall under the last figure, as in 1728, the unite will be left placed at 1, in the middle of the Line, and the Root, Square and Cube will fall forward toward the end of the Line.

If the last Prick shall fall under the last Figure but one, as in 17280; the unite may be placed at 1, in the beginning of the Line, and the Cube in the second length: or the unite may be placed at 10, in the end of the Line, and the Cube in the first length.

But if the last Prick shall fall on the last Figure but two, as in 172800; then, place the unite always at 10 in the end of the Line: so the Root, Square and Cube will all fall backward and be found in the second length.

8. To find the Cubique Root of a Number.

9. The Root being given to find the Cube Number of that Root.

In the Extraction of a Cubique Root, it is usual to set Pricks under the first Figure, the fourth, the seventh and the tenth, and so forward omitting two, and pricking the third from the right hand toward the left; and as many Pricks as fall to be under the Cubique Numbers, so many Figures shall be in the Root. So that if the Number given be less than 1000, the Root shall be only of one Figure; if less than 1000000, it shall be but of two Figures; if above these, and less than 1000000000, it shall be but three Figures, &c. whereupon the Lines of Solids are divided, first into 1000 parts, and if the Numbers given be greater than 1000 the first Division (which before did signify only one) must signifie 1000, and the whole Line shall be 1000000: if yet the Number given be geater than 1000000, the first Division must now signifie 1000000, and the whole Line be esteemed at 1000000000 parts, and if these be too little to express the Numbers given, as oft as we have recourse to the beginning, the whole Line shall increse itself a thousand times.

By these means, if the last Prick, to the left hand, shall fall under the last Figure, the Number shall be reckoned at the beginning of the Lines of Solids from 1 to 10, and the first Figure of the Root shall be always either 1 or 2. If the last Prick shall fall under the last Figure but one, then the Number shall be reckoned in the middle of the Line of Solids, between 10 and 100, and the first Figure of the Root shall be always either 2, or 3, or 4. But if the last Prick shall fall under the lsat Figure but two, then the Number given shall be reckoned at the end of the Line of Solids, between 100 and 1000.

This being considered, when a Number is given, and the Cubique Root required, set one Foot of the Compasses in the Center of the Sector, extend the other in the Line of Solids to the Points of the Number given: For this Distance applied to one of the Lines of Lines, shall shew what the Cubique Root is, without opening the sector.

• So the nearest Root of 8490000, is about 204.
• The nearest Root of 84900000, is about 439.
• The nearest Root of 849000000, is about 947.

On the contrary, a Number may be cubed, if first we extend the Compasses to the Number given, in the Line of Lines, and apply the Distance to the Lines of Solids, as may appear by the former Eyamples.

10. Three Numbers being given, to find a fourth in a triplicated Proportion.

As like Superficies do hold a duplicated proportion, so like Solids in a triplicated Proportion of their homologal Sides: and therefore the same Work is to be observed here on the Lines of Solids, as before in the Lines of Superficies, as may appear by these two Examples.

If a Cube whose side is 4 inches, shall be 7 pound weight, and if it be required to know the weight of a Cube whose sides is 7 inches; here the Proportion would be,

• As 4 are to a Cube of 7:
• So 7 to a Cube of 37 ½.

And if I took 7 out of the Line of Solids, and put it over in 4 and 4, in the Lines of Lines, his Parallel between 7 and 7, measured in the Lines of Solids, would be 37 ½; and such is the weight required.

If a Bullet of 27 pound weight, have a Diameter of 6 inches, and it be required to know the Diameter of the like Bullet, whose weight is 125 pounds, here the Proportion would be,

• As the Cubique Root of 27, is unto 6,
• So the Cubique Root of 125, is unto 10.

And if I took 6 out of the Line of Lines, and put it over in 27, and 27 of the Lines of Solids, his Paralell between 125 and 125 measured in the Line of Lines, would be 10; and such is the length of the Diameter required.

End if the first Book.