The Second Book of the Sector
CHAP. II.
Of the general Use of Sines and Tangents.
1. The Radius being known, to find the right Sine of any Ark or Angle.
If the Radius of the Circle given be equal to the lateral Radius, that is to the whole Line of Sines on the sector, there needs no farther work, but to take the other Sines also out of the Side of the sector. But if it be either greater or lesser, then let it be made a parallel Radius, by applying it over in the Lines of Sines, between 90 and 90, so the Parallel taken from the lateral Sines, shall be the Sine required.
As if the given Radius be AC, and it were required to find the Sine of 56 gr. and his Complement agreeable to that Radius.
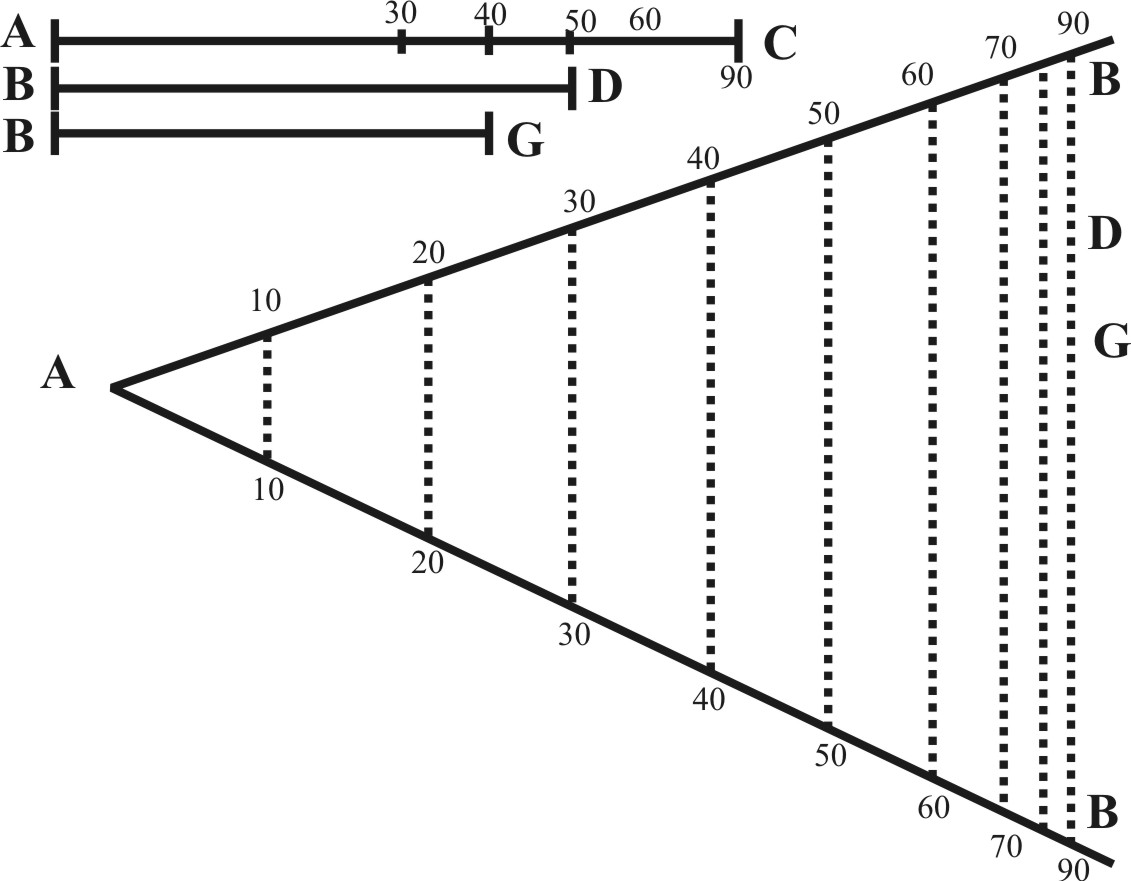
Let AB, AB represent the Lines of Sines on the Sector, and let BB the Distance between 90 and 90, be equal to the given Radius AC. Here the Lines A 40, A 50, A 90 may be called the lateral Sines of 40, 50, and 90, in regard to their place on the side of the Sector. The Lines between 40 and 40, between 50 and 50, between 90 and 90, may be called the parallel Sines 40, 50, and 90, in regard they are parallel one to the other. The whole Sine of 90 gr. here standing for the Semidiameter of the Circle, may be called the Radius. And therefore if AC be put over in the Line of Sines in 90 and 90, and so made a Parallel Radius, his parallel Sine between 50 and 50 shall be BD, the Sine of 50 required. And because 50 taken out of 90, the Complement is 40, his parallel Sines between 40 and 40 shall be BG, the Sine of the Complement which was required.
2. The right Sine of any Ark being given to fins the Radius.
Turn the Sine given into a parallel Sine, and his parallel Radius shall be the Radius required.
As if BD were the given Sine of 50 gr. and it were required to find the Radius, let BD be made a parallel Sine of 50 gr. by applying it over the Lines of Sines between 50 and 50, so his parallel Radius between 90 and 90 shall be AC, the Radius required.
The Radius of a Circle, or the right Sine of any Ark, being given, and a straight Line resembling a Sine, to find the quantity of that unknown Sine.
Let the Radius or right Sine given be turned into his Parallel, then take the right Line given, and carry it parallel to the former, till it stay in like Sines, so the number of Degrees and minutes where it stayeth, shall give the quantity of the Sine required.
As if BD were the given Sine of 50 gr. and BG the straight Line given, first I make BD a parallel Sine of 50 gr. then keeping the Sector at this Angle, I carry the Line BG parallel, and find it to stay in no other but 40 and 40, and therefore 40 gr. is the Quantity required.
4. The Radius or any right Sine being given, to find the versed Sine of any Ark.
If the Ark, whose Versed Sine is required, be less than the Quadrant, take the Sine of the Complement out of the Radius, and the Remainder shall be the Sinus Versus, the Versed Sine of that Ark.
As if AB being the lateral radius, it were required to find the Versed Sine of 40 gr. here the Sine of the Complement is A 50, and therefore B 50 is the Versed Sine required. Or if I reckon from B at the end of the Sector, toward the Center, the Distance from 90 to 80 is the Versed Sine of 10 gr. from 90 to 70, the Versed Sine of 20 gr. from 90 to 60 is the Versed Sine of 30 gr. and so the rest.
If AD be the given Sine of 50 gr. and it be required to find the Versed Sine of 50 gr. here because AD is unequal to the lateral Sine of 50 gr. I make it a Parallel. And first I find the Radius AC, then the Sine of the Complement A 40, which being taken out of AC, leaveth C 40, for the Versed Sine of 50 gr. which was required.
But if the Ark whose Versed Sine is required, be greater than the Quadrant, his Versed Sine also is greater than the Radius, by the right Line of his excess above 90 gr.
As if AC being the Radius given, it were required to find the Versed Sine of 130 gr. here the excess above 90 gr. is 40 gr. and therefore the Versed Sine required is equal to the Radius AC and A 40, both being set together.
5. The Diameter or Radius being given, to find the Chords of every Ark.
The Sines may be fitted many ways to serve for Chords, 1. A Sine being the half of the double Ark, if the Sine is doubled: it giveth the Chord of the double Ark, a Sine of 10 gr. doubled givetrh a Chord of 20 gr. and a Sine of 25 gr. being doubled giveth a Chord of 50 gr. and so the rest; As here BD, the Sine of BC, an Ark of 40 gr. being doubled, giveth BE the Chord of BCE, which is an Ark of 80 gr. Wherefore if the Radius of the Circle given be equal to the lateral Radius, let the Sector be opened unto his length, so that both the Lines of Sines may make but one direct Line: so the Distance of the Sines between 10 and 10 shall be a Chord of 20, the Distance between 20 and 20 shall be a Chord of 40, and the Distance between 30 and 30, shall be a Chord of 60, and so the rest.
2. Because a Sine is the half of the Chord of the double Ark, the Proportion holdeth.
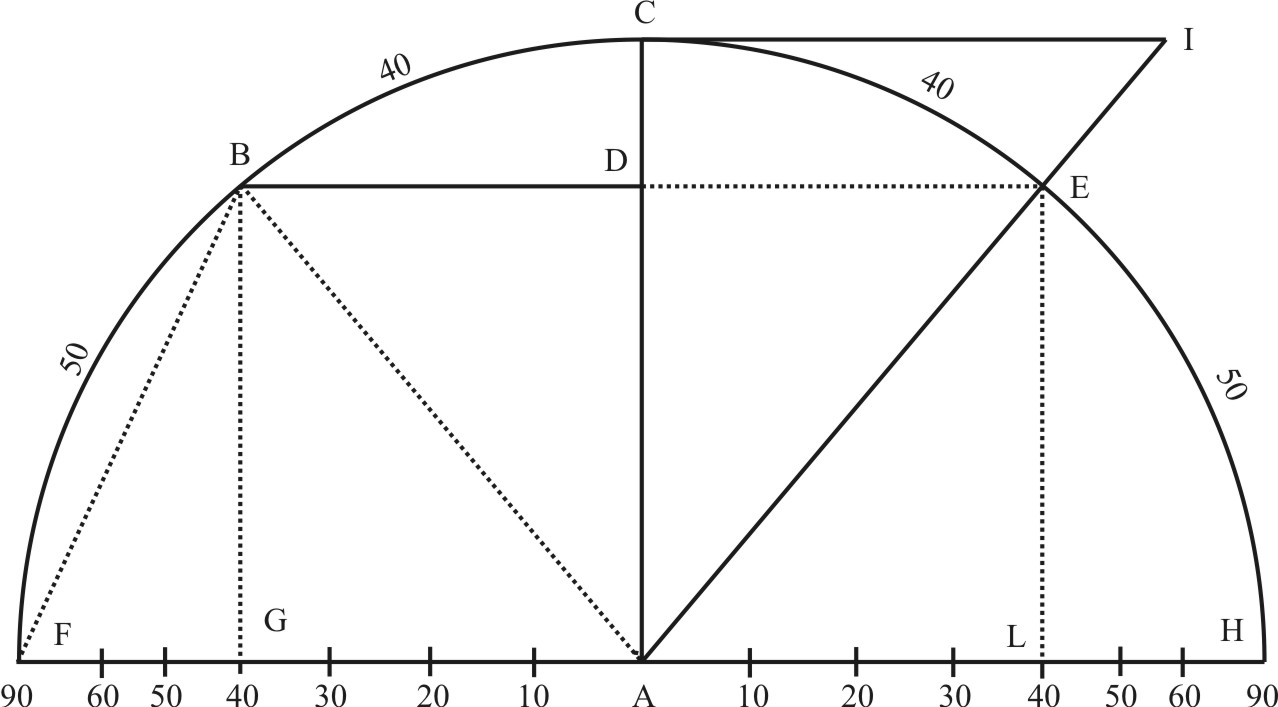
As the Diameter FH unto the Radius AH , so the Cord BE unto the Sine DE, or the Chord GL unto the Sine AL, and then if the Radius AH be put for the Diameter, which is a Chord of 180 gr. the Sine DE or AL, shall serve for a Chord of 80 gr. and the Semiradius which is the Sine of 30 gr. shall serve for a Chord of 60 gr. and go for the Semidiameter of a Circle, and so the rest. So that by these means we shall not need to double the Lines of Sines as before, but only to double the Numbers. And to this purpose I have subdivided each degree of the Sines into two, that so they might shew how far the half degrees do reach in the Sines, and yet stand for whole degrees when they are used as Chords.
Wherefore if the Radius of the Circle given be equal to the lateral Semiradius (the Sine of 30 gr. and Chord of 60 gr.) there needs no farther works, then to take the Sine of 10 gr. for a Chord of 20 gr. and a Sine of 15 gr. for a Chord of 30 gr. &c.
But if the Radius of the Circle given be either greater or lesser than the lateral Semiradius, take the Diameter of it, and make it a Parallel Chord of 180 gr. by applying it over the Lines of Sines between 90 and 90, or take the Radius or Semidiameter, which is equal to the Chord of 60 gr. and make it a parallel Radius of 60 gr. by applying it over in the Sines of 30 and 30, and keep the Sector at this Angle. The Parallels taken from the lateral Chords shall be the Chords required.
As if the Diameter of a Circle given were the Line AB, and it were required to find the Chord of 80 gr. First I make AB a parallel Chord of 180 gr. or the half of it a parallel Chord of 90 gr. so his Parallel LG, doth give me FG the Chord of 80 gr. which was required.
3. Seeing that as the Sine of the Complement of the half Ark is unto the Radius, so the Sine of the same whole Ark is unto the Chord of it: If we seek but for one single Chord, we may find it without either doubling the Sines, or doubling the Number. For applying over the Radius given in the Sine of the Complement of half the Ark required, his parallel Sine shall be the Chord required.
As if the Semidiameter of the Circle given were AC, and it were required to find the Chord of 40 gr.the half of 40 gr. is 20 gr. the Complement of 20 gr. is 70 gr. Wherefore I make AC a parallel Sine of 70 gr. and his parallel Sine GL, doth give me FG, the Chord of 40 gr. agreeable to the Semidiameter AC.
Having two right Lines resembling the Chord and Versed Sine, to find the Diameter and Radius.
Let the two right Lines given be AB, resembling the Chord, GD the Versed Sine of a Circle, whose Arch AGB is unknown, and let it be required to find the Diameter GF.
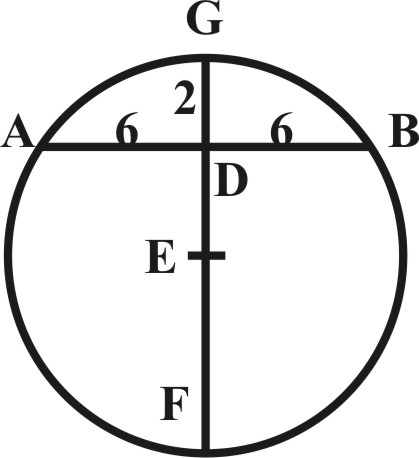
Having two Lines given, the first GD, the second AD, the half of AB, we may find a third in continual Proportion (by the sixth or nineth Proposition of the Lines) and that shall be the Line DF (18) the Sum whereof and of GD gives the Diameter GF (20) and the half thereof is the Radius (EG).
6. The Chord of any Ark being given, to find the Diameter and the Radius.
Turn the Chord given unto a parallel Chord, and his parallel Semiradius shall be the Semidiameter, and the parallel Radius shall be the Diameter.
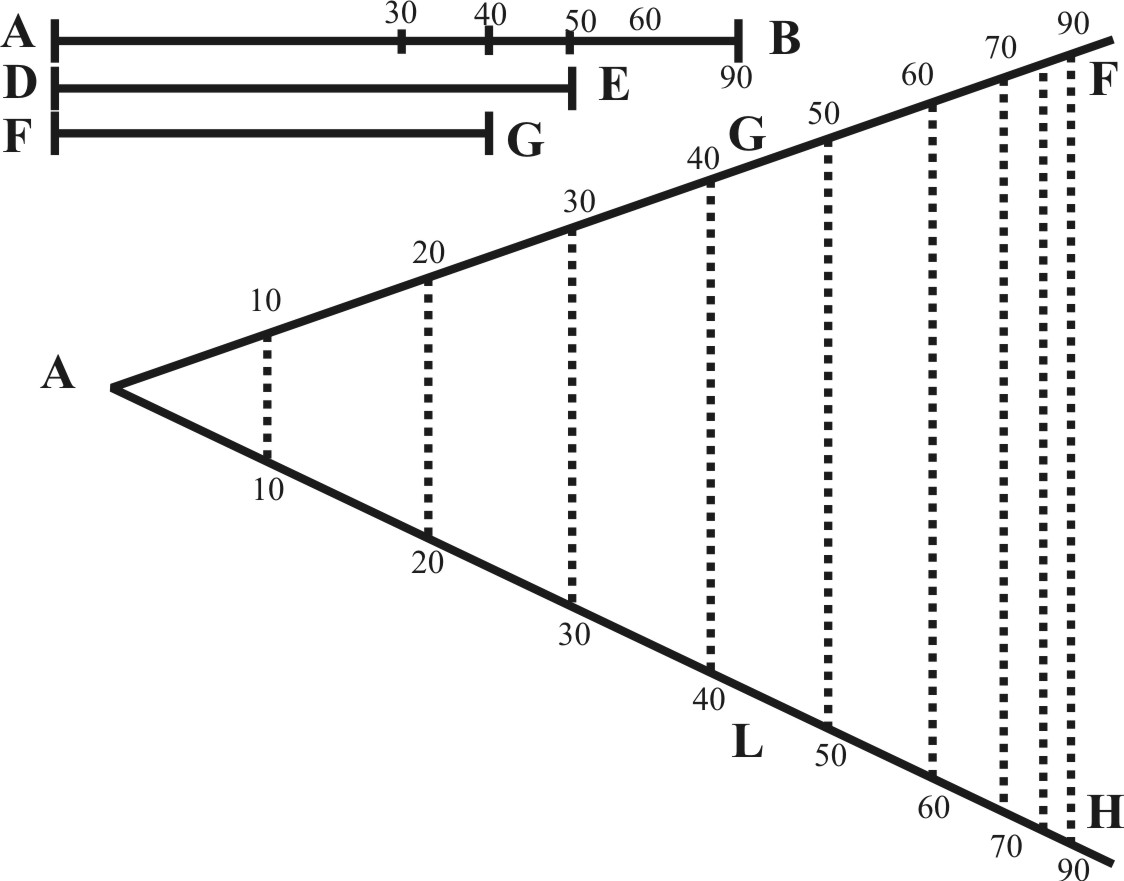
As if FG be the Chord of 80 gr. I put this over in G and L, the Sine of 40, and Chord of 80 gr. and the parallel Chord of 180 gr. giveth me AB the Diameter required.
Or if I turn the Chord given into an parallel Sine of the same quantity, his parallel Sine of the Complement of half the Ark, doth give me the Semidiameter.
As if FG be the given Chord of 40 gr. I put it over in G and L, the Sines of 40 gr. then because the half of 40 gr. is 20 gr. and the Complement of 20 gr. is 70 gr. I take out the parallel Sine of 70 gr. and it giveth me AB for the Semidiameter, agreeable to that Chord of 40 gr.
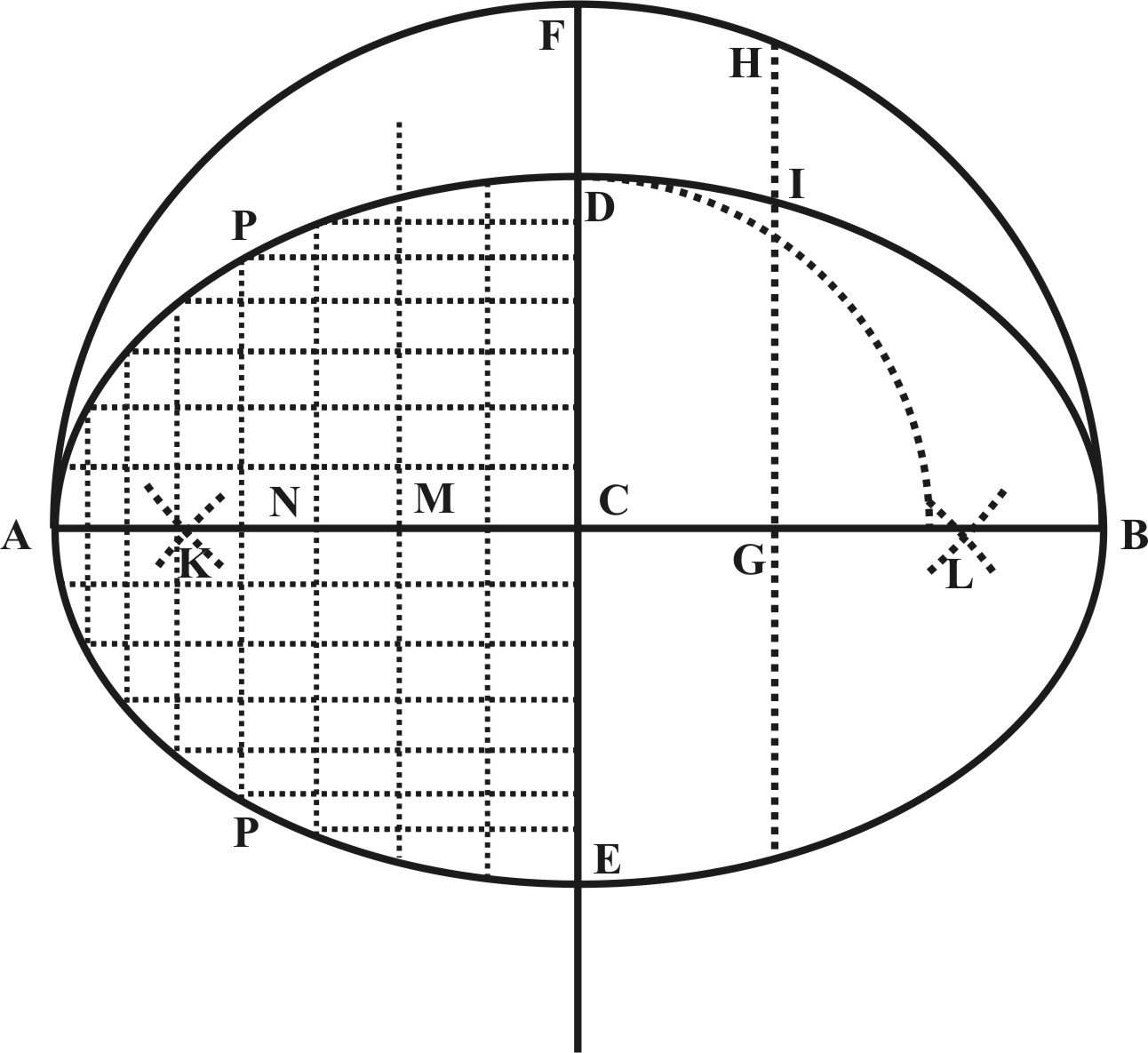
Having the Diameter of an Ellipsis to describe the same upon a plain.
If each Semidiameter be divided, in such sort, as the Line of Sines is divided upon the Sector, and right Lines drawn through each division Perpendicular to those Semidiameters like unto Sines; The Points where the Sines drawn through the one Semidiameter do meet the Sines of the Complement drawn through the other Semidiameter, shall be Points through which the Ellipsis is to be drawn.
Let the Diameters be AB, DE, one crossing the middle of the other in the Point C. Divide first the Semidiameters CA, CB; then the Semidiameters CD, CE, like unto the Lines of Sines upon the Sector, by the eighth Proposition of Lines: So, the ellipsis shall be drawn through the Points at the meeting of the Sines of 10 and 80, of 20 and 70, of 30 and 60, &c.
Or (without the help of the Line of Sines) we may draw the Circle AFB upon the Center C, and the Semidiameter AC, for so, crossing the Diameter AB with several Perpendicular Lines continued unto the Circumference of the Circle, if we divide these Perpendiculars on either side of the Diameter in such sort as the greater Semidiameter CF is divided by the lesser, in the Point D, and draw a Line winding through all these Points, the Line so drawn shall be the Ellipsis.
Or (without the help of the Sector) we may with the Radius AC, upon the Centers D and E, describe two occult Arches meeting in the Points K and L. Then taking between C and K, any number of Points M N, we may from the Centers K and L, with the Semidiameter MB describe four occult Arches; and with the Radius AM, and the same Centers K and L, cross them again with four Arches in the Pouints at O. In like manner, from the same centers K and L, with the Radius NB, we may describe other four occult Arches; and with the Radius AN, and the former centers cross them again, with four Arches in the Points at P, and so draw the Ellipsis through the Points O P, &c.
This is (in effect) as we should tye a thread about A and L, and then draw it easily from the Point A round about the two former Centers K and L, until it were brought to the Point A again which is also an easie way to describe an Ellipsis.
The distance of these former Points from either Semidiameter may be set down in Numbers. For supposing the lesser Semidiameter CD, to be 10, the greater (CB) to be 16, (or otherwise divided into any Number of known Points,) If we have the proportion between CG and CB, we may find the length of the Perpendicular GI.
If the Proportion be as 1 to 2, the Perpendicular will be 8.66.
If the Proportion be as 2 to 3, the perpendicular will be about 7.45.
| As the greater Semidiameter | CB |
| to the part given | CG |
| So 100000, the Radius | CB |
| to the Sine of | CG |
| whose Complement is | GH |
| As the Radius | CF |
| to the Sine of the Complement | GH |
| So the lesser Semidiameter | CD |
| to the Perpendicular | GI |
The same may also be found without knowing the Sines. For the Perpendicular GH is a mean Proportional between AG and GB: which being known
As CF unto ED, so is GH unto GI.
7. To open the Sector to the quantity of any Angle given.
8. The Sector being opened, to find the quantity of the Angle.
It is one thing to open the Edges of the Sector to an Angle, and another thing to open the Lines on the Sector to the same Angle. For the Line of Lines on the one side, and the Lines of Sines on the other side do make an Angle of 2 gr. when the Sector is close shut, and the Edges do make no Angle at all. So likewise the Lines of Superficies and the Lines of Solids do make an Angle of 10 gr. which are to be allowed to the Edges.
The Lines of Lines may be opened to a right Angle, if the whole Line of 100 parts be applied over in 80 and 66.
The Line of Sines may be opened to a right Angle, if the large Secant of 45 gr. be applied over in the Sines of 90 gr. or if the Sine of 90 gr. be applied over in the Sines of 45 gr. or if the Sine of 45 gr. be applied over in the Sines of 30 gr.
If it be required to open those Lines to any other Angle, take out the Chord thereof, and apply it over in the Semiradius, and those Lines shall be open to that Angle.
As if it were required to open the Sector in the Lines of Sines to an Angle of 40 gr. take out the Chord of 40 gr. and open it to the Sector in the Chord of 60 gr. so shall the Lines of Sines be opened to the Angle required. Or if the same Chord of 40 gr. be applied over between 50 and 50, in the Lines of Lines, they shall also be opened to the same Angle. If it be applied over in 25 of the Lines of Superfcies, or 125 in the Lines of Solids, they also shall be opened to the same Angle: because the Chord of 60 gr. or Sine of 30 gr. and 50 in the Lines of Lines, and 25 in the Lines of Superficies, and 125 in the Solids, are all of the same length with the Semiradius.
Or if the Semiradius by applied over between the Sine of 30 gr. and the Sine of the Complement of the Angle required, it will open the Lines of Sines to that Angle.
As if the Semiradius be applied over in the Sines of 30 gr. and the Sine of 50 gr. it shall open the Lines of Sines to an Angle of 40 gr.
On the contrary, if the Sector be opened to an Angle, and it be required to know the quantity thereof, open the Compasses to the Semiradius, and setting one foot in the Sine of 30 gr. turn the other to ward the other Line of Sines, and it shall fall there in the Complement of the Angle; if it fall on 50 gr. the Angle is 40 gr. if on 60 gr. the Angle is 30 gr. &c.
Or take over the parallel Chord of 60 gr. and measure it in the lateral Chord, and it shall there shew the quantity of the Angle, As if the Sector be opened to an Angle, I should take over the parallel of 30 gr. of the Sines, and 60 gr. of the Chords, and measure it in the lateral Chords, find it to be 40 gr. the Angle comprehended between the Lines of Sines is 40 gr. but the Angle between the edges of the Sector is 2 gr. less, and therefore but 38 gr.
9. To find the quantity of any Angle given.
If out of the Angular Point, to the quantity of the Semiradius, be described an occult Ark that may cut both sides of the Angle, the Chord of this Ark measured in the lateral Chord, shall give the quantity of the Angle.
Let the Angle be BAC: first I take the Semiradius with the Compasses, and setting one foot in A, I cut the sides of the Angle in B and C; then I take the Chord BC, and measure it in the lateral Chord, and I find it to be 11 gr. and 15 min. and such is the quantity of the Angle given.

Or if the ark be described out of the Angulat Point at any other distance, let the Semidiameter be turned into a parallel Chord of 60 gr. then take the Chord of this Ark, and carry it parallel, till it cross in the like Chords: so the place where it stayeth shall give the quantity of the Angle.
As in the former example, if I make the Semidiameter AB a parallel Chord to 60 gr. and then keeping the Sector at that Angle, carry the Chord BC parallel, till it stay in like Chords; I shall find it to stay in no other but 11 gr. 15 min. and such is the Angle BAC.
10. Upon a right Line, and a Point given in it, to make an Angle equal to any Angle given.
First out of the Polar given describe an Ark, cutting the same Line: then by the 5 Prop. afore, find the Chord of the Angle given agreeable to the Semidiameter and inscribe it into this Ark: so a right Line drawn through the point given, and the end of this Chord, shall be the side that makes up the Angle.
Let the right Line given be AB, and the Point given in it be A, and let the Angle given be 11 gr. 15 min. Here I open the Compasses to any Semidiameter AB, (but as oft as I may conveniently to the lateral Semiradius) and setting one foot in A, I describe an occult Ark BC; then I seek out the Chord of 11 gr. 15 min. and taking it with the Compasses, I set one foot in B, the other crosseth the Ark in C, by which I draw the Line AC, and it makes up the Angle required.
11. To divide the Circumference of a Circle into any parts required.
If 360, the measure of the whole Circumference, be divided by the Number of parts required, the Quotient giveth the Chord, which being found will divide the Circumference.
So a Chord of 120 gr. will divide the Circumference into three equal parts; a Chord of 90 gr. into four parts, a Chord of 72 gr. into five parts; a Chord of 60 gr. into six parts; a Chord of 51 gr. 26 min. into seven parts; a Chord of 45 gr. into eight parts; a Chord of 40 gr. into nine parts; a Chord of 36 gr. into ten parts; a Chord of 32 gr. 44 min. into eleven parts; a Chord of 30 gr. into twelve parts.
In like manner if it is required to divide the Circumference of the Circle whose Semidiameter is AB, into 32; first I take the Semidiameter AB, and make it a parallel Chord of 60 gr, then because 360 gr. being divided by 32 the Quotient will be 11 gr. 15 min. I find the parallel Chord of 11 gr. 15 min. and this will divide the Circumference into 32.
But here the parts being many, it were better to divide it first into fewer, and after to come over it again. As first to divide the Circumference into 4, and then each 4 parts into 8, or otherwise, as the parts may be divided.
12. To divide a right Line by extreme and mean proportion.
The Line to be divided by extreme and mean proportion, hath the same proportion to his greater Segment, as in Figures inscribed in the same Circle, the side of an Hexagon a figure of six Angles, hath to a side of a Decagon a figure of ten Angles: but the side of a Hexagon is a Chord of 60 gr. and the side of a Decagon is a Chord of 36 gr.
Let AB be the Line to be divided: if I make AB a parallel Chord of 60 gr. and to this Semidiameter find AC a Chord of 36 gr. this AC shall be the greater Segment, dividing the whole Line in C, by extreme and mean proportion. So that,
- As AB the whole, is unto AC the greater Segment:
- so AC the greater Segment, unto CB the lesser Segment.
Or let AC be the greater Segment given: if I make this a parallel Chord of 36 gr. the correspondent Semidiameter shall be the whole Line AB, and the difference CB the lesser Segment.
Or let CB be the lesser Segment given: if I make this a parallel Chord of 36 gr. the correspondent Semidiameter shall be the greater Segment AC, which added to CB, gives the whole Line AB.
To avoid doubling of Lines or Numbers, you may put over the whole Line in the Sines of 72 gr. and the parallel Sine of 36 gr. shall be the greater Segment.
Or if you put over the whole Line in the Sines of 54 gr. the parallel Sine of 30 gr. shall be the greater Segment, and the parallel sine of 18 gr. shall be the lesser Segment.