The Second Book of the Sector
CHAP. IV
Of the Resolution of right-lined Triangles.
In all Triangles there being six parts, viz. three Angles, and three sides, any three of them being given, the rest may be found by the Sector.
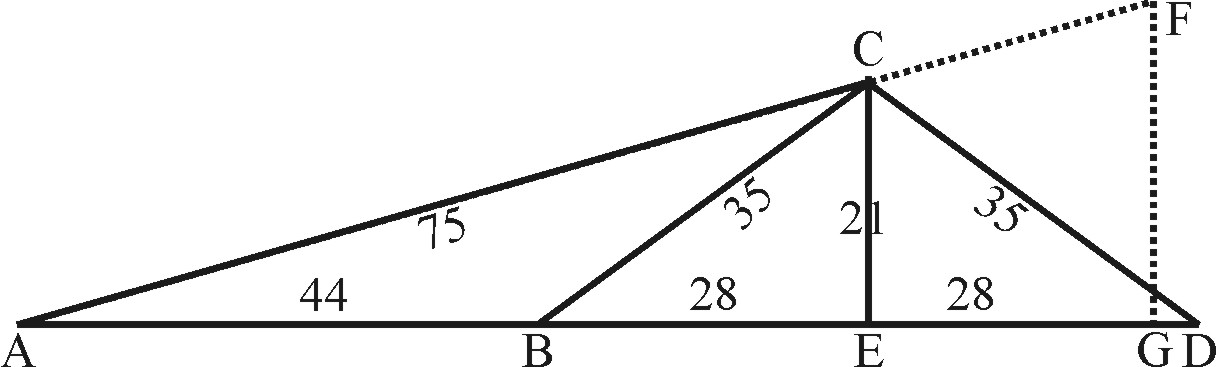
As may appear by the Prop. following, wherein for our practise we may use these Triangles CEA, CEB, CED, all which are Rectangles in E. And AGF Rectangled in G. All the rest consist of Oblique Angles.
| Ang. | Gr. | M. | S. | Lin. | Parts. |
| E | 90 | 0 | 0 | AC | 75 |
| G | 90 | 0 | 0 | AF | 100 |
| A | 16 | 15 | 36 | FG | 28 |
| D | 36 | 52 | 12 | CE | 21 |
| B | 36 | 52 | 12 | CD | 35 |
| B | 143 | 7 | 48 | BB | 35 |
| AFG | 73 | 44 | 12 | AG | 96 |
| ACE | 73 | 44 | 12 | AE | 71 |
| ACB | 20 | 36 | 36 | AB | 44 |
| BCE | 53 | 7 | 48 | BD | 28 |
| ECD | 53 | 7 | 48 | AD | 28 |
| BCD | 106 | 15 | 36 | BE | 56 |
| ACD | 126 | 52 | 12 | ED | 100 |
In a Rectangled Triangle.
1. To find the Base, both sides being given.
Let the Sector be opened in the Line of Lines to a right Angle (as before was shewed Chap. 2. Prop. 7.) then take out the sides of the Triangle, and lay them, one on one Line, the other on the other Line, so as they meet in the Center, and mark how far they extend. For the Line taken from the terms of their extension, shall be the Base required, viz. the side opposite to the right Angle.
Or add the squares of the two sides (as in Prop. 4. Superfic.) and the side of the compound Square shall be the Base. (Note that I call, the longest side of the Triangle the Base.)
As if the Lines AE, CE, should be the sides about the right Angle, and it were required to find the Base subtending the right Angle.
First, I set the Line of Lines to a right Angle by applying the whole Line of 10 from 6 in the one Line, to 8 in the other. Then if the greater of the two Lines given be less than the Line of Lines, I take the greater of them AE, and transfer it with the Compasses into one of the Lines of Lines, and find that, in my Sector (which is 14 Inches long, and so, the Line of Lines, almost 7 Inches) it reaches from the Center to 518.
Again, I take the lesser Line CE, and transfer it into the other Line of Lines, and find, that it reacheth from the center unto 151, wherefore I take the distance from 151 unto 518, and such is the length of, the Base AC required.
It either of the Lines given be too large for the Sector, then I may measure them by Feet or Inches, as suppose I find the length of AE to be about 720, and of CE 210. Then in the Line of Lines (being set, one Perpendicular to the other as before) I extend the Compasses from 210 unto 720; and measure this extent in the Line of Lines, find it to be 750 parts, wherefore I prick down 750 parts in the Line AC, from the same Scale by which I measured AE, and CE. So, this Line AC shall be the Base required.
In working by the Line of Superficies, I need no opening of the Sector. For taking the Line CE with my Compasses, and measuring it in the Line of Superficies upon my Sector, I find it near 13 parts.
Then taking the Line AE, I find it to be about 269. These two being added togethetr make 292: and this extent is the length of the Base AC required.
2. To find the Base, by having the Angles, and one of the sides given.
Take the side given, and turn it into the parallel Sine of his opposite Angle; so the parallel Radius shall be the Base.
As if the Line AE were the side of a Rectangle Triangle opposite to an Angle of 73 gr. 45. and it were required to find the Base.
First I take the side AE with my Compasses, and set it over in the Sines of 73 gr. 45 m. So, the Parallel Radius taken from between 90 and 90, will give the Base AC required.
If the side given be such as cannot well be fitted over the Sines of his opposite Angle, I may measure it by feet or inches, and suppose I find the length of AE to be 720, then would I take 720 parts out of the Line of Lines, and make it a Parallel Sine of 73 gr. 45. So, the Parallel Radius taken from between 90 and 90, and measured in the Line of Lines will be found to be about 750 parts: Wherefore, I prick down 750 in the Line AC, by the same Scale, whereby I measured AE: and this Line AC shall be the Base required.
3. To find a side by having the Base and the other side given.
Let the Sector be opened in the Lines of Lines to a right Angle, and the side given laid on one of those Lines from the Center: then take the Base with a pair of Compasses, and setting one foot in the term of the given side, turn the other to the other Line of the Sector, and it shall there shew the side required.
Or take the Square of the side out of the Square of the base (as in Prop. 4. Superfic.) and the side of the remaining Square shall be the side required.
Thus having AC for the Base, and CE, for the side of a Rectangle Triangle, the other side will be founf to be AE.
Or, if AC, being measured, be 750, and CE, 210, the other side AE will be found to be 720.
4. To find a side having the Base, and the Angles given.
Take the Base given, and make it a Parallel Radius, so the parallel Sines of the Angles, shall be the opposite sides required.
Thus in the Rectangle AEC, if AC be made a Parallel Radius, the Parallel Sine of 73 gr. 45 , will give the side AE; and the Parallel Sine of 16 gr. 15 will give the other side CE.
5. To find a side having the other side and the Angles given.
Take the side given, and turn it into his Parallel Sine of his opposite Angle: so the Parallel Sine of the Complement shall be the side required.
Thus in the Rectangle DEC, if CE be made a Parallel Sine of 53 gr. 8 m. the parallel Sine of 36 gr. 52 m. will give the side ED, and the Parallel Sine of 90 gr. Will give the Base CD.
6. To find the Angles by having the Base and one of the sides given.
First, take out the Base given, and laying it on both sides of the Sector, so as they may meet in the Center, and mark how far it extendeth. Then take out the lateral Radius, and to it open the Sector in terms of the Base. This done, take out the side given, and place it also on the same Lines of the Sector from the Center. For the Parallel taken in the terms of this side, shall be the Sine of his opposite Angle.
Or take the base given, and make it a Parallel Radius; then take the side given, and carry it parallel to the Base, till it stay in like Sines: so they shall give the quantity of the opposite Angle.
Thus in the Rectangle AEC, having the Base AC, and the side AE, you may find the Angle CAE, to be 16 gr. 15 m.
7. To find the Angles by having both sides given.
Take out the greater side, and lay it on both sides of the Sector, so as they meet in the Center, and mark how far it extendeth. Then take the other side, and to it open the Sector in the trems of the greater side; so the Parallel radius shall be the Tangent of the lesser Angle. The third Angle is always known by the Complement.
Thus in the Rectangle DEC, having the sides CE, and ED, you may find the lesser angle ECD to be 36 gr. 52 m. and therefore the other Angle EDC to be 53 gr. 8 m.
8. The Radius given, to find the Tangent and Secant of any Ark.
9. The Tangent of any Ark being given, to find the Secant thereof, and the Radius.
10. The Secant of any Arc being given, to find the Tangent thereof, and the Radius.
The Tangent, and the Secant, together with the Radius of every Ark, do make a right Angle Triangle; whose sides are the Radius and Tangent, and the Base always the Scant; and the Angles always known by reason of the given Arks. As in the Rectangle AEC, if on the Center A, and the Semidiameter AE, you describe a Circle, then make AE, to the Radius, and EC, a Tangent of 16.15 and AC a Secant of 16 gr. 15 m.
If you describe a Circle on the Center C, and Semidiameter CE, then is CE the Radius and EA a Tangent of 73 gr. 45 m. and CA a Secant of 73.45.
Wherefore the Solution is the same with those before.
11. In any right-lined Triangle whatsoever, To find a side by knowing the other two sided, and the Angle contained by them.
Let the Sector be opened in the Lines of Lines to the Angle given as I shewed before, Chap. 2. Prop. 7. Then take out the sides of the triangle, and laying them one on the one Line, the other on the other, so as they meet in the Center, mark how far they extend. For the Line taken between the terms of their Extension, shall be the third side required.
As if AC and AD were two sides of a right lined Triangle containing an Angle of 16 gr. 16 m. and it were required, to find the third side subtending this Angle.
First, I set the Lines to an Angle of 16 gr. 16 m. by applying the Sine of 8 gr. 8 m. over in the Points of 50 and 50, in the Line of Lines. That done, I take the longer Line AD, and transfer it with my Compasses into one of the Line of Lines, and find it to reach from the Center to 720.
Again, I take the lesser Line AC, and transfer it into the other Line of Lines, where it reacheth from the Center to 540, wherefore, I take the distance from 540 to 720, and such id the length of the third side CD required.
Or (if the Lines be given in measure) AD 100, and AC 75. I extend the Compasses from 100 to 75, and measuring this extent in the Line of Lines, find it to be 35. Whereupon I take 35 parts out of the Scale, by which AC, and AD were measured, and prick them down in the Line CD. So this Line CD shall be the third side required.
12. To find a side by having the other two sides, and one of the adjacent Angles, so it be known which of the Angles is Acute or Oblique.
Let the Sector be opened in the Line of Lines to the Angle given, and the adjacent side laid on one of those Lines from the center: then take the other side with a pair of Compasses, and setting one foot in the term of the former given side, turn the other to the other Line of the Sector which here representeth the side required, and it shall cross it in two places; but with which of them is the term of the side required, must be judged by the Angle.
As if in the Triangle following, the side AC being given, and the side CD and the Angle CAD 16 gr. 16 m. it were required to find the side AD.
First, I open the Sector in the Line of Lines to an Angle of 16 gr. 16 m. and laying the adjacent side from the Center A, find where it extendeth in C. Then I take the other side CD with the Compasses, and setting one foot in C, and turning the other to the other Line of the Sector, I find that it doth cross it both in B and D.
Or, (if the Lines be given in measure) AC 75, and CD 35; I may take 35 out of the Line of Lines, and setting one foot in 75, I shall find the other foot to cross the other Line of the Sector, both at 44 (answerable to AB) and at 100 (answerable to AD).
So that it is uncertain whether the side required be AB or AD, only it may be judged by the Angle. For if the inward Angle where they cross be Obtuse, the side required is the lesser; if it be Acute, it is the greater.
13. To find a side by having the Angles, and one of the other sides given.
Take the side given, and turn it into the Parallel Sine of his opposite Angle; so the Parallel Sines of the other Angle shall be the opposite sides required.
As if in the Triangle ABC, having the side AD, and knowing the Angle CAB to be 16 gr. 16 m. and the Angle ABC to be 143 deg. 8 m. it were required to find the other two sides, AC and BC.
The three Angles of a right-lined Triangle, are always equal to 180 gr. Wherefore I add 16 gr. 16 m. unto 143 gr. 8 m. and by the remainder to 180 gr find the third Angle ACB opposite to the known side AB, to be 20 gr. 36 m. Then I take the side AB, and make its Parallel Sine to be 20 gr. 36 m.
So, his parallel Sine of 16 gr. 16 m. will be the side BC; and the Parallel Sine of 143 degr. 8 m. will be the side AC.
Or if measured the side AB, I find to be 44; I may take 44 parts, either out of the Line of Lines, or of any other Scale of equal parts, and make it a Parallel Sine of 20 gr. 36 m. So his Parallel Sine of 16 gr. 16 m. measured in the same Scale, will give 35 for the length of the side BC: and the Parallel Sine of 36 gr. 52 m. will give 75, for the length of the other side AC.
When the Angle comes to be above 90 gr. The Sine of 80 gr. doth stand for a Sine of 100 gr. And the Sine of 70 gr. For a Sine of 110 gr. And so the rest; for those, which are their Complements to 180 gr.
14. To find the proportion of the sides by having the three Angles.
Take the lateral Sines of the Angles, and measure them in the Line of Lines. For the numbers belonging to those Lines do give the proportion of the sides.
Thus, in the two equi-angle Triangles AEC, AGF, if you take the lateral Sine of 90 gr. For the right Angle at E and G, and measure it in the Line of Lines, you shall find it to be 100. Then take the lateral Sine of 16 gr. 16 m. for the common Angle in A, you shall find it to be 28. Take lateral Sine of 73 gr. 44 m. For the third Angle at C and F, you shall find it to be 96. Such therefore is the proportion of the sides.
As 100 : 96.28: So are 75 : 72.21
15. To find an Angle, by knowing the Three Sides.
Let the two containing sides be laid on the Lines of the Sector, from the Center, one on one Line, and the other on the other; and let the third side, which is opposite of the Angle required, be fitted over in their terms, so shall the Sector be opened in those Lines to the quantity of the Angle required.
The quantity of this Angle is found as in Chap. 2. Prop 8. Thus having the three sides of the Triangle ACD, to find the Angle in A, I take the two containing sides AD, AC, and transfer them with my Compasses into the Line of Lines: where I find the one to reach from the Center, to 72; the other, to 54.
Then I take CD, (the side opposite to the Angle in A) and set that over between 72 and 54.
Or if the three sides be given in measure AD 103; AC 75; CD 35: I might take 35 for the side CD out of the Line of Lines, and set that over from 100 to 75. This done I take the distance between 50 and 50 and measuring it in the Line of Sines I find it to be about 8 gr. 8 m. the double thereof is 16 gr. 16 m. the Angle required.
16. To find an Angle, by having two sides, and one adjacent Angle.
First take out the side opposite to the Angle given, and laying it on both sides of the Sector, so as they meet in the Center, mark down how far it extendeth; then take out the lateral Sine of the Angle, and to it open the Sector in the terms of the first side: this done take out the other side given, and place it also on the same Lines of the Sector from the Center, for the Parallels taken in the terms of this side; shall be the Sine of the Angle opposite to the second side.
Or take out the side opposite to the Angle given, and make it a Parallel Sine of that Angle: then take the other side given and carry it Parallel to the former, till it stay in like Sines: so they shall give the quantity of the Angle opposite to the second side.
Thus in the Triangle ACD, knowing two sides AC, CD, with the Angle CAD opposite to the side CD, you may find the Angle ADC opposite to the other known side AC, to be about 36 gr. 52 m.
17. To find an Angle by having two sides, and the Angle contained by them.
First find the third side by the 11 Prop. And then the Angles may be found by the 15 or 16 Prop.
For observation of Angles, the Sector may have sights set on the movable foot: so that by looking through them, the edges of the Sector may be applied to the sides of the Angle.
For measuring of the side of lesser Triangles, any Scale may suffice, either of feet, or inches, or lesser parts. But for greater Triangles, especially for plotting of grounds. I hold it fit to use a chain of four Perches in length, each Perch divided into 25, and the whole Chain an hundred Links, wherein, if the whole Chain be (according to 16 ½ foot in a Perch) 66 foot, (that is 792 inches) each several Link will be seven inches and 28/100.
If (according to 18 in the Perch) the whole Chain be 71 feet in length (that is 864 inches) then each several Link will be eight inches and 66/100.
For so the length being multiplied into the breadth, the five last Figures give the content in Roods and perches by this Table; the other Figures towards the left hand do shew the number of Acres directly.
As in a long Square, where the length is 24 Chains ½ the breadth is 13 Chains ½ the usual way is, to resolve the Chains into Perches: So the length is 97 Perches, and the breadth 54 Perches. These multiplied one into the other make 5238 square perches, and those (divided by 160) give 32 Acres, 2 Roods, and 38 perches for the content required.
But, reckoning by Chains and Links, the length is 24 Chains 25 Links, the breadth 13 Chains 50 Links. These multiplied one into the other make 32.73750 square Links. Then, cutting off the five last Figures, I find 32 Acres 73750 lin. Such as an 100000 do make an Acre, Of which 70000 are equal to two Roods 32 Perches: and the rest 3750 equal to 6 Perches more (as appeareth by this Table). So, the whole content is 32 Acres, 2 Roods, 38 Perches, as before.
| Link | R | P |
| 100000 | 4 | 0 |
| 90000 | 3 | 24 |
| 80000 | 3 | 8 |
| 70000 | 2 | 32 |
| 60000 | 2 | 16 |
| 50000 | 2 | 0 |
| 40000 | 1 | 24 |
| 30000 | 1 | 8 |
| 20000 | 0 | 32 |
| 10000 | 0 | 16 |
| 9375 | 0 | 14 |
| 8750 | 0 | 13 |
| 7500 | 0 | 12 |
| 6875 | 0 | 11 |
| 6250 | 0 | 10 |
| 5625 | 0 | 9 |
| 5000 | 0 | 8 |
| 4375 | 0 | 7 |
| 3750 | 0 | 6 |
| 3125 | 0 | 5 |
| 2500 | 0 | 4 |
| 1875 | 0 | 3 |
| 1250 | 0 | 2 |
| 624 | 0 | 1 |