The Second Book of the Sector

CHAP. V
Of the Resolution of Spherical Triangles.

For our practise in Spherical Triangles, let A be the Equinoctial Point, AB an Ark of the Ecliptick, representing the Longitude of the Sun in the beginning of , BC an Ark of the Suns Declination from the Equator, and AC an Ark of the Equator representing the right Ascension.

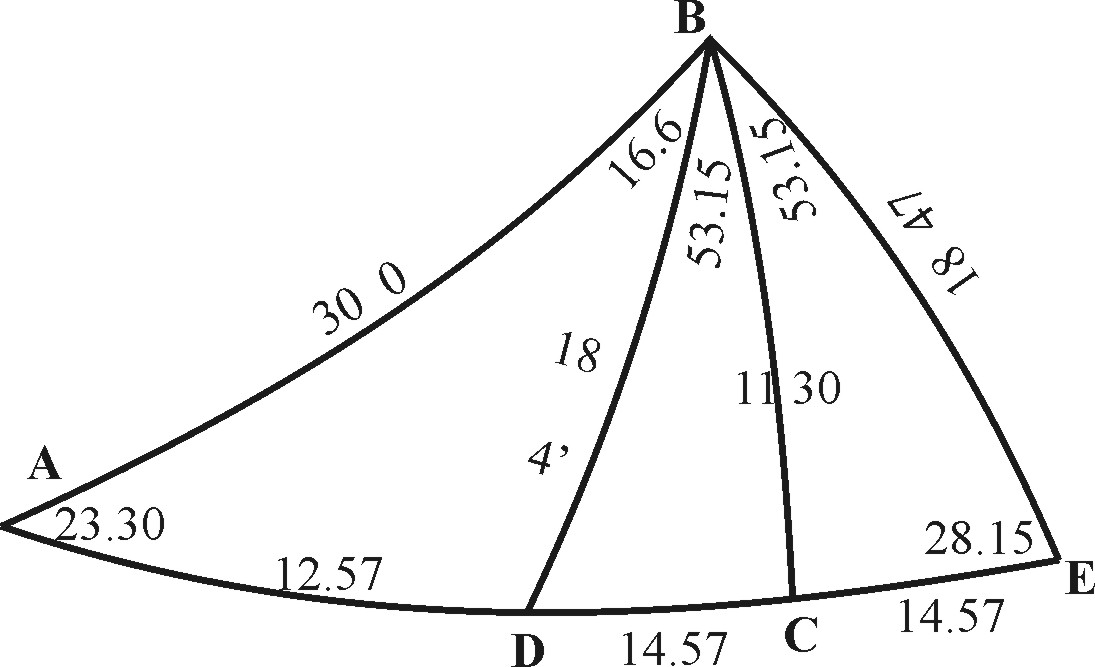
Let BD be an Ark of the Horizon, representing the Amplitude of the Suns rising from the East, and BE an Ark of the Horizon for his setting from the West: so DC shall be the difference of the Ascension, and CE the difference of Descension; AD the Oblique Ascension, and AE the Oblique Descension of the same place of the Sun in our Latitude at Oxford of 51 gr. 45 m. whose Complement 38 gr. 15 m. is the Angle at E and D. The Triangles ACB, DCB, ECB, are Rectangled in C: the other ABD, AEB, consist every way of Oblique Angles.

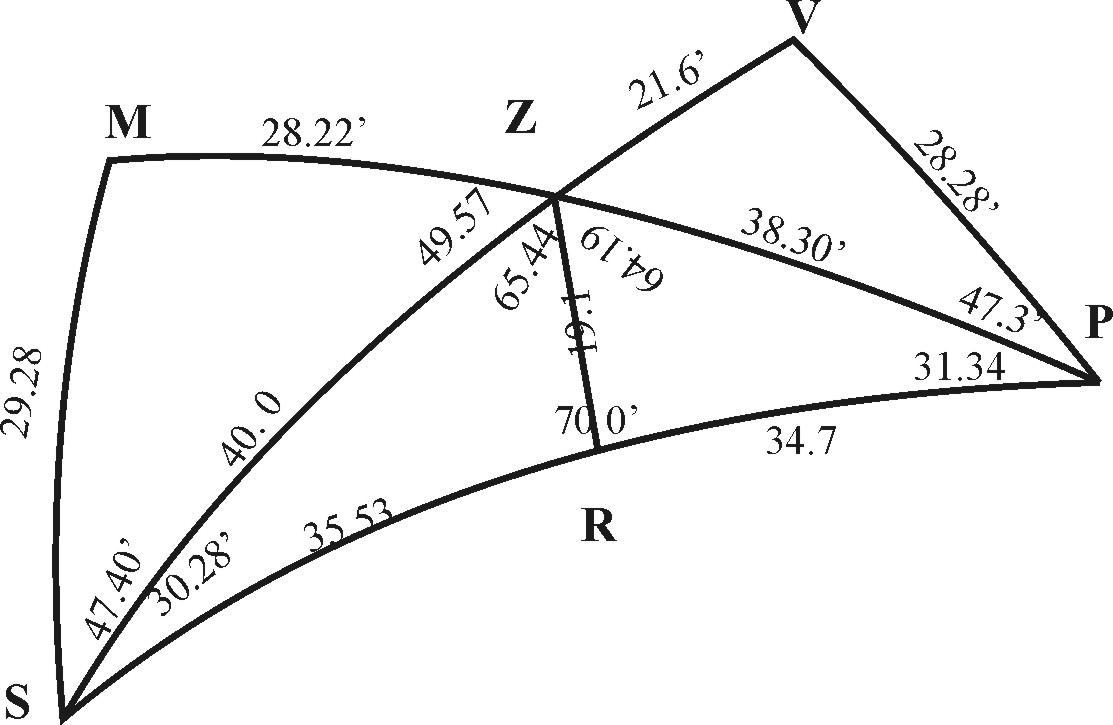
Or, to fit an Example nearer to the Latitude of London. Let ZPS represent the Zenith, Pole, and Sun, ZP being 38 gr. 30 m. the Complement of the Latitude, PS 70 gr. The Complement of the Declination, and ZS 40 gr. The Complement of the Suns Altitude. The Angle at Z shall shew the Azimuth, and the Angle at P, the Hour of the Day from the Meridian. Then if from Z to PS we let down a Perpendicular ZR, we shall reduce the Oblique Triangle into two Rectangle Triangles ZRP, ZRS. Or if from S to ZP we let down a Perpendicular SM, we shall reduce the same into two other Triangles, SMZ, SMP, Rectangled at M: whatsoever is said of any of these Triangles, the same holdeth for all other Triangles in the like cases.

For the Resolution of each of these, there be several ways. I only chuse those which are fittest for the Sector, wherein if that be remembered which before is shewed in the general use of the Sector concerning Lateral and Parallel entrance, it may suffice only to set down the Proposition of the three parts given, to the fourth required, and so shew first by the Sines alone.

1. To find a side, by knowing the Base, and the Angle opposite to the required side.

• As the Radius is to the Sine of the Base:
• So the Sine of the opposite Angle to the Sine of the side required.

*As in the Rectangel ACB, having the Base AB, the place of the Sun 30 gr. from the Equinoctial Point, and the Angle BAC of 23 gr. 30 m. the greatest Declination, if it were required to find the side BC the Declination of the Sun.

(*In Rectangled Triangles, the side opposite to the Rectangle is called the Base.)

Take either the lateral Sine of 20 gr. 30 m. and make it a Parallel Radius; so the Parallel Sine of 30 gr. taken and measured in the side of the Sector, shall give the side required 11 gr. 30 m. Or take the Sine of 30 gr. and make it a Parallel Radius; so the Parallel Sine of 23 gr. 30 m. taken and measured in the lateral Sines, shall be 11 gr. 30 m. as before.

So in the Triangle ZPS, having ZP 38 gr. 30 m. and the Angle P 31 gr. 34 m- given, we shall find the Perpendicular ZR to be 19 gr. 1 m. or having PS 70 gr. and the said Angle P 31 gr. 34 m. given, we may find the Perpendicular SM to be 29 gr. 28 m.

2. To find the side by knowing the Base and the other side.

• As the Sine of the Complement of the side given is to the Radius:
• So is the Sine of the Complement of the Base to the Sine of the Complement of the side required.

So in the Rectangle ACB, having AB 30 gr. and BC 11 gr. 30 m. given, the side AC will be found 27 gr. 54 m.

Or in the Rectangel ZRP, having ZP 38 gr. 30 m. and ZR 29 gr. 1 m given, the side RP will be found 34 gr. 7 m.

3. To find a side, by knowing the two Oblique Angles.

• As the Sine of either Angle to the Sine of the Complement of the other Angle:
• So is the Radius to the Sine of the Complement of the side opposite to the second Angle.

So in the Rectangle ACB having CAB for the first Angle 23 gr. 30 m. and ACB, for the second 69 gr. 22 m. the side AC will be found 27 gr. 54 m. Or making ABC the first Angle, and CAB the second, the side BC will be found 11 gr. 30m.

4. To find the Base, by knowing both the sides.

• As the Radius to the Sine of the Complement of the one side:
• So the Sine of the Complement of the other side, to the Sine of the Complement of the Base required.

So in the Rectangle ACB having AC 27 gr. 54 m and BC 11 gr. 30 m. the Base AB will be found 30 gr.

5. To find the Base by knowing the one side, and the Angle opposite to that side.

• As the Sine of the Angle given, to the Sine of the side given:
• So is the Radius to the Sine of the Base required.

So in the Rectangel BCD, knowing the Latitude and the Declination, we may find the Amplitude; as having BC the side of the Declination 11 gr. 30 m. and BDC the Angle of the Complement of the Latitude 38 gr. 15 m. the Base BD, which is the Amplitude, will be found to be 18 gr. 47 m.

6. To find an Angle, by the other Oblique Angle, and the side opposite to the inquired Angle.

• As the Radius, to the Sine of the Complement of the side:
• So the Sine of the Angle given, to the Sine of the Complement of the Angle required.

So in the Rectangle ACB, having the Angle BAC 23 gr. 30 m. and the side AC 27 gr. 54 m. the Angle ABC will be found 69 gr. 21 m.

7. To find an Angle, by the other Oblique Angle, and the side opposite to the Angle given.

• As the Sine of the Complement of the side to the Sine of the Complement of the Angle given:
• So is the Radius, to the Sine of the Angle required.

So in the Rectangle ACB, havin BAC 23 gr. 30 m. and BC 11 gr. 30 m. the Angle ABC will be found 69 gr. 21 m.

8. To find and Angle, by the Base, and the side opposite to the inquired Angle.

• As the Sine of the Base is to the Radius:
• So the Sine of the side to the Sine of the Angle required.

So in the Rectangle BCD, having BD 18 gr. 47 m. and BC 11 gr. 30 m. the Angle BCD will be found 38 gr. 15 m.

These eight Propositions have been wrought by the Sines alone; those which follow require joint help of the Tangent.

And forasmuch as the Tangent could not well be extended beyond 63 gr. 30 m. I shall set down two ways for the resolution of each Proposition; so that if one will not hold, the other may.

9. To find a side, by having the other side, and the Angle opposite to the required side.

1. As the Radius to the Sine of the side given:
   So the Tangent of the Angle, to the Tangent of the side required
2. As the Sine of the side given, is to the Radius:
   So the Tangent of the Complement of the Angle to the Tangent of the Complement of the side required.

So in the Rectangle ACB, having the side AC 27 gr. 54 m. and the Angle BAC 23 gr. 30 m. the side BC will be found to be 11 gr. 30 m.

10. To find a side, by having the other side, and the Angle next the inquired side.

1. As the Tangent of the Angle, to the Tangent of the side given:
   So is the Radius to the Sine of the side required.
2. As the Tangent of the Complement of the side, to the Tangent of the complement of the Angle:
   So is the Radius to the Sine of the side required.

This and the like, where the Tangent standeth in the first place, are best wrought by parallel entrance. And so in the Rectangle BCD, having BC the side of Declination 12 gr. 30 m. and BDC the Angle of the Complement of the Latitude 38 gr. 15 m. the side DC, which is the Ascensional difference, will be found 14 gr. 57 m.

By the Ascensional difference is given the time of the Suns rising and setting, and the length of the day: allowing an hour for each 15 gr. And four minutes of time for each several degree. As in the example, the difference between the Suns Ascension in a right Sphere, which is always at six of the clock, and his Ascension in our Latitude being 14 gr. 57 m. it sheweth that the Sun riseth very near an hour before six, because of the Northern Declination; or after six, if the Sun be declining to the Southward.

11. To find a side by knowing the Base, and the Angle adjacent next to the inquired side.

1. As the Radius, to the Sine of the Complement of the Angle:
   So the Tangent of the Base, to the Tangent of the side required.
2. As the Sine of the Complement of the Angle, is to the Radius:
   So is the Tangent of the Complement of the Base, to the Tangent of the Complement of the side required.

So in the Rectangle ACB, knowing the place of the Sun from the next Equinoctial Point, and the Angle of his greatest Declination, we may find his right Ascension: viz. the Base AB 30 gr. And the Angle BAC 23 gr. 30 m. being given, the right Ascension AC will be found 27 gr. 54 m.

12. To find the Base by knowing the Oblique Angles.

• As the Tangent of the one Angle, to the Tangent of the Complement of the other Angle:
• So is the Radius, to the Sine of the Complement of the Base.

So in the Rectangle ACB, having BAC 23 gr. 30 m. and ABC 69 gr. 21 m. the Base AB will be found 30 gr.

13. To find the Base, by one of the sides, and the Angle adjacent next that side.

1. As the Radius, is to the Sine of the Complement of the Angle:
   So the Tangent of the Complement of the side, to the Tangent of the Complement of the Base.
2. As the Sine of the Complement of the Angle, is to the Radius:
   So the Tangent of the side given, to the tangent of the Base required.

14. To find an Angle, by knowing both the sides.

1. As the Radius, is to the Sine of the side next the inquired Angle:
   So the Tangent of the Complement of the opposite side, to the Tangent of the Complement of the Angle required.
2. As the Sine of the side next the inquired Angle, is to the Radius:
   So the Tangent of the opposite side, to the Tangent of the Angle required.

So in the Rectangle ACB, having AC 27 gr. 54 m. and BC 11 gr. 30 m. the Angle at A will be found 23 gr. 30 m. and the Angle at B 69 gr. 21 m.

15. To find the Angle, by the Base, and the side adjacent to the required Angle.

1. As the Tangent of the Complement of the side, to the Tangent of the Complement of the Base:
   So is the Radius, to the Sine of the Complement of the Angle required.
2. As the Tangent of the Base, to the Tangent of the side:
   So is the Radius, to the sign of the Complement of the Angle required.

So in the Rectangle BCD, having the Base BD 16 gr. 47 m. and the side BC 11 gr. 30 m. the Angle DBC between them will be found 53 gr. 15 m.

16. To find an Angle, by knowing the other Oblique Angle, and the base.

1. As the Radius, to the Sine of the Complement of the Base:
   So the Tangent of the Angle give, to the Tangent of the Complement of the Angle required.
2. As the Sine of the Complement of the Base, is to the Radius:
   So the Tangent of the Complement of the Angle given, to the Tangent of the Angle required.

So in the Rectangle ACB, having the Angle at A 23 gr. 30 m. and the Base AB 30 gr. The Angle ABC will be found 69 gr. 12 m.

These sixteen Cases are all that can fall out in a Rectangle Triangle: those which follow do hold in any Spherical Triangle whatsoever.

17. To find a side, opposite to an Angle given, by knowing one side, and two Angles, whereof one is opposite to the given side, the other to the side required.

• As the Sine of the Angle opposite to the side given, is to the Sine of the side given:
• So the Sine of the Angle opposite to the side required, to the Sine of the side required.

So in the Triangle ABE, having the place of the Sun, the latitude, and the greatest Declination, we may find the Amplitude. As having AB 30 gr. BAE 23 gr. 30 m. and ABE 38 gr. 15 m. the side BE which is the Amplitude, will be found 18 gr. 47 m.

18. To find an Angle opposite is a side given, by having one Angle and two sides, one opposite to the given Angle, the other to the Angle required.

• As the Sine of the side opposite to the Angle given, is to the Sine of that Angle given:
• So the Sine of the side opposite to the Angle required, to the Sine of the Angle required.

So in the Triangle ZPS, having the Azimuth, and Latitude, and Declination, we may find the hour of the day. As having PZS 130 gr. 3 m. PS 70 gr. and ZS 40 gr. the Angle ZPS, which sheweth the hour from the Meridian, shall be found 31 gr. 34 m.

19. To find an Angle by knowing the three sides.

This Proposition is most useful, but most difficult of all others: as in Arithmetrick, so by the Sector, yet may be performed several ways.

1. According to Regiomontanus and others

• As the Sine of the lesser side, next the Angle required, to the difference of the versed Sines of the Base, and difference of the sides:
• So the Radius, to a fourth proportional.

• Then as the Sine of the greater side next the Angle required, is to that fourth proportional:
• So is the Radius, to the versed Sine of the Angle required.

So in the Triangle ZPS, having the side PS, the Complement of the Declination 70 gr. 0 m. the side ZP the Complement of the Latitude 38 gr. 30 m. and the Base ZS the Complement of the Altitude 40 gr. the Angle of the hour of the day ZPS will be found 31 gr. 34 m. which is 2 h. 6 m,. from the Meridian.

For the Base being 40 gr. 0 m. and the difference of the sides 38 gr. 30 m. and 70 gr. 0 m. being 31 gr. 30 m., the difference of their versed Sines will be the same with the distance between the right Sine of 50 gr. and 58 gr. 30 m,. This difference I take out, and make it a Parallel Sine of the lesser side 38 gr. 30 m. so the Parallel Radius will be the fourth proportional. Then coming to the second operation, I make this fourth proportional a Parallel Sine of the greater side of 70 gr, 0 m. and take out this Parallel Radius. For this measured from 90 gr. toward the Center, will be the versed Sine of 31 gr. 34 m.

In the like sort in the same Triangle ZPS, having the same Complements given, the Angle PZS which is the Azimuth from the North part of the Meridian, will be found 130 gr. 3 m. For here the Base opposite to the Angle required being 70 gr. and the difference of the sides 38 gr. 30 m. and 40 gr. being 1 gr. 30 m,. the difference of their versed Sines will be the same with the distance between the right Lines of 20 gr. and 88 gr. 30 m. This difference I take and make it a Parallel Sine of the lesser side 38 gr. 30 m. so the Parallel Radius will be the fourth proportional. Then coming to the second operation, I make this fourth proportional a Parallel Sine of the greater side 40 gr. and take out this Parallel Radius; for this measured from 90 gr. beyond the Center, in the Line if Sines, stretched forth at their full length, will be the versed Sine of 130 gr. 3 m.

2. I may find an Angle by knowing three sides, by that which I have elsewhere demonstrated upon Barth. Pitiscus, and that at one operation in this manner.

• As the Sine of the greater side, is to the Secant of the Complement of the other side:
• So the difference of Sines of the Complement of the Base, and the Ark compounded of the lesser side with the Complement of the greater, to the versed Sine of the Angle required.

So in the same Triangle ZPS, having the same Complements given, the Angle at P, which sheweth the hour from the Meridian, will be found as before, 31 gr. 34 m.

For the sides being 38 gr. 30 m. and 70 gr. 0 m. I take the Secant of the Complement of 38 gr. 30 m. and make it a Parallel Sine of 70 gr. the keeping the Sector at this Angle, I consider that the Complement of 70 gr. being 20 gr. added unto 38 gr. 30 m. the compound side (which is here the Meridian Altitude) will be 58 gr. 30 m. and that the Base being 40 gr. the difference of Sines of the compound side, and the Complement of the Base will be (as before) the distance between the Sines of 50 gr. and 58 gr. 30m. Wherefore I take out this difference, and lay it on both Lines of Sines from the Center: so the parallel taken in the terms of this difference, and measured from 90 gr. toward the Center, doth give the versed Sine of 31 gr. 34 m.

This example of finding the hour of the day might otherwise have been proposed in these terms,

• As the Sine of the Complement of the Declination, is to the Secant of the Latitude:
• So the difference between the Sine of the Altitude proposed, and the Sine of the Meridian Altitude, to the versed Sine of the hour from the Meridian:

Then the Latitude being 51 gr. 30 m. the Declination 20 gr. Northward, and the Altitude 50 gr. the work would be the same as before.

The other Angles PZS, PSZ, may be found in the same sort; but having the sides and one Angle, it will be sooner done by that which we shewed before in the 18 Prop.

20. To find a side, by knowing the three Angles.

If for the greater Angle, we take his Complement to 180 gr. the Angles shall be turned into sides, and the sides into Angles, and the operation shall be the same, as in the former Prop.

As in the Triangle ZPS, having the Angle ZPS 31 gr. 34 m. ZSP 30 gr. 28 m. and PZS 130 gr. 3 m. I would take the greater Angle of 130 gr. 3 m. out of 180 gr. and there remains 49 gr. 57 m. Then as I had a Triangle of three known sides, one of 31 gr. 34 m. another of 30 gr. 20 m. and a third of 49 gr. 57 m. I would seek the Angle opposite to one of these sides, by the last Prop. So the Angle which is thus found, would be the side, which is here required.

21. To find a side, by having the other two sides, and the Angle comprehended.

This Proposition being the converse of the nineteenth, may be wrought accordingly: but the best way both for it and those which follow, is to resolve them into two Rectangles, by letting down a Perpendicular, as was shewed in the first Prop.

So in the Triangle ZPS, having ZP the Complement of the Latitude, and PS the Complement of the Declination, with ZPS the Angle of the hour from the Meridian, we may find ZS the Complement of the Altitude of the Sun.

For having let down the perpendicular ZR, by the first Prop. we have two Triangles, ZRP, ZRS, both rectangle at R. Then may we find the side PR, either by the second, or tenth, or eleventh Prop. which taken out of PS, leaveth the side RS: with this RS and ZR we may find the Base ZS by the fourth Prop.

Or having let down the Perpendicular SM, we have two Rectangle Triangles SMZ, SMP. Then may we find MP, from which if we take ZP, there remaineth MZ: but with MZ and SM, we may find the Base ZS.

22. To find a side, by having the other two sides, and one of the Angles next to the inquired side.

So in the Triangle ZPS, having ZP, the Complement of the Latitude, and PS the Complement of the Declination, with PZS the Angle of the Azimuth, we may find ZS the Complement of the Altitude of the Sun.

For having ZP, and the Angle at Z, we may to SZ produced, let down a Perpendicular PV. Then we have two Rectangle Triangles PVZ, PVS, wherein if we find the sides VZ, VS, and take the one out of the other, there remain the side required ZS.

23. To find a side, by having one side, and the two Angles next the inquired side.

So in the Triangle ABD, having AB the place of the Sun, and BAD the Angle of the greatest Declination, and ADB the Angle of the Equator with the Horizon, we may find AD the Oblique Ascension.

For having let down BC the Perpendicular of the Declination, we have two Rectangle Triangles, ACB, DCN. Then may we find AC the right Ascension, and DC the ascensional difference; and comparing the one with the other, there remaineth AD.

24. To find a side, by knowing two Angles, and the side inclosed by them.

So in the Triangle ZPS, having the Angles at Z and P, with the side intercepted ZP, we may find the side PS. For having let down the perpendicular PV, we have two Rectangles PVZ, PVS. Then may we find the Angle VPZ, either by the seventh, or fifteenth, or sixteenth Prop. which added to ZPS, maketh the Angle VPS, with this VPS, and PV, we may find the Base PS, according to the 23 Prop.

25. To find an Angle by having the other two Angles and the side inclosed by them.

So in the Triangle ZPS, having the Angles at Z and P, with the side intercepted ZP, we may find the other Angle ZSP. For having let down the Perpendicular ZR, we have two Rectangels ZRP, ZRS. Then may we find the Angle PZR by the sixteenth Prop. and that compared with PZS, leaveth the Angle RZS: with this RZS, and ZR, we may find the Angle required ZSR, according to the sixth Proposition.

26. To find an Angle, by having the other two Angles, and one of the sides next the inquired Angle.

So in the triangle ABD, having the Angles at A and D, with the side AB, we may find the Angle ABD. For having let down the Perpendicular BC, we have two Rectangles, ACB, DCB. Then may we find the Angles ABC, DBC, and take DBC out of ABC; for so there remaineth the Angle required ABD.

27. To find an Angle, by knowing two sides, and the Angle contained by them.

So in the Triangle ZPS, having the sides ZP, PS, with the Angle comprehended ZPS, we may find the Angle PZS. For having let down the perpendicular SM, we have two Rectangles SMZ, SMP. Then we find the side MP, and taking ZP out of MP, there remaineth MZ: with this MZ and the Perpendicular MS, we may find the Angle MZS, by the fourteenth Prop. This Angle MZS, taken out of 180 gr. there remaineth PZS.

28. To find an Angle, by knowing the two sides next it and one of the other Angles.

So in the Triangle ZPS, having the sides ZP, and PS, with the Angle PZS, we may find the Angle ZPS; For having let down the perpendicular PV, we have two Rectangles PVZ, PVS. Then may we find the Angles VPZ, VPS: and taking VPZ out of VPS, there remaineth ZPS, which was required.

These 28 Cases are all that can fall out in any Spherical Triangle: if any do not presently understand them, let them once more read over the use of the Globes, and they shall soon become easie unto them.