The Second Book of the Sector
CHAP. VI
Of the Use of the Meridian Line in Navigation.
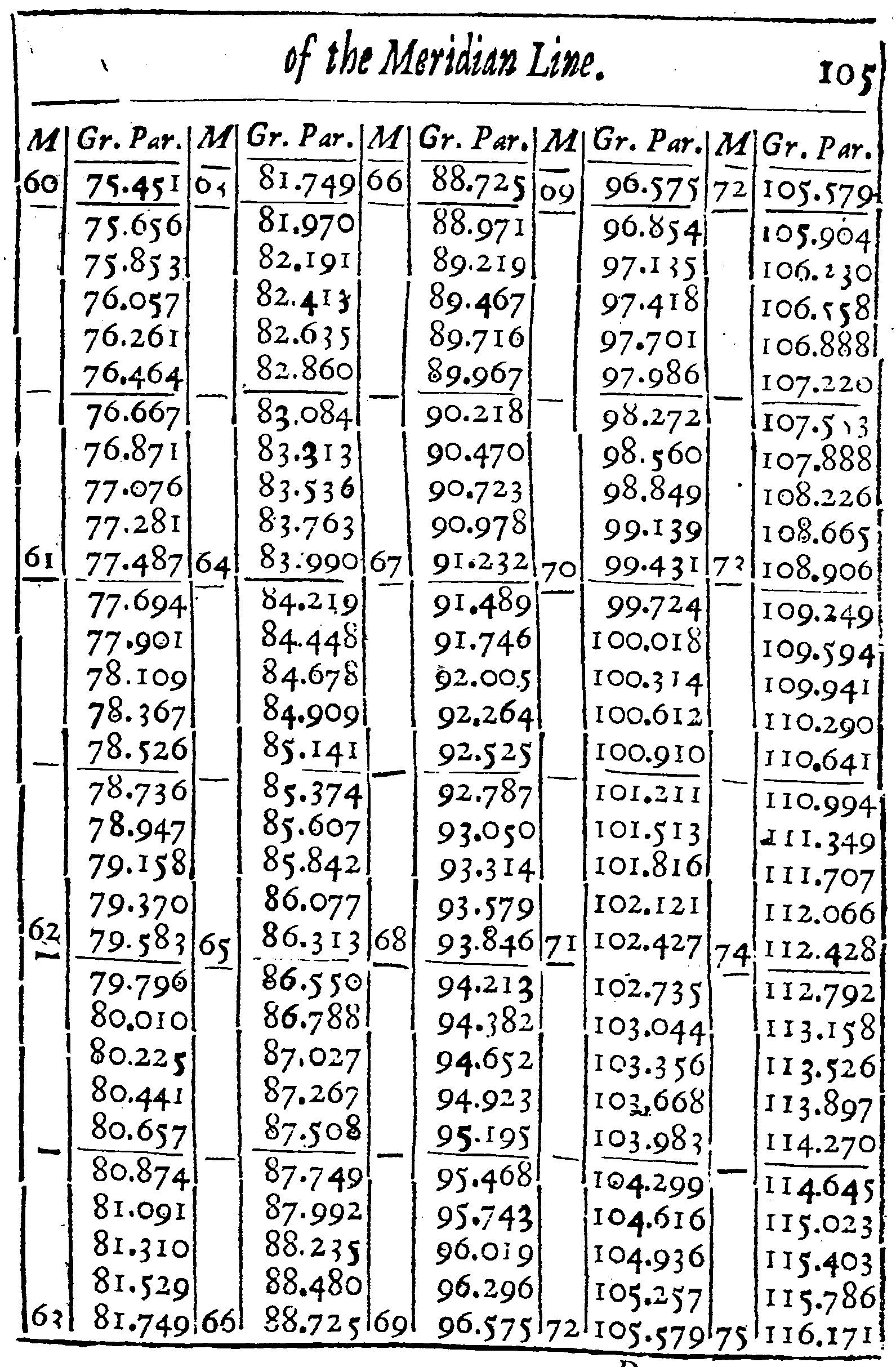
The Meridian Line is here set on the side of the Sector stretched forth at full length, on the same Plane with the Line of Lines and Solids, and is divided unequally toward 87 gr. (whereof 70 gr. are about one half) in such sort as the Meridian in the Chart of Mercators Projection. The Use of it may be,
1. To divide a Sea-chart according to Mercators Projection.
If a degree of the Equator on the Sea-chart, be equal to the hundred part of the Line of Lines in the Sector, the degrees of the Meridian upon the Sector, shall give the like degrees upon the Sea-chart: if otherwise they be unequal, then may the Meridians of the Sea-chart be divided in such sort as the Line of Meridians is divided on the Sector, by that which we shewed before in the 8 Prop. of the Line of Lines.
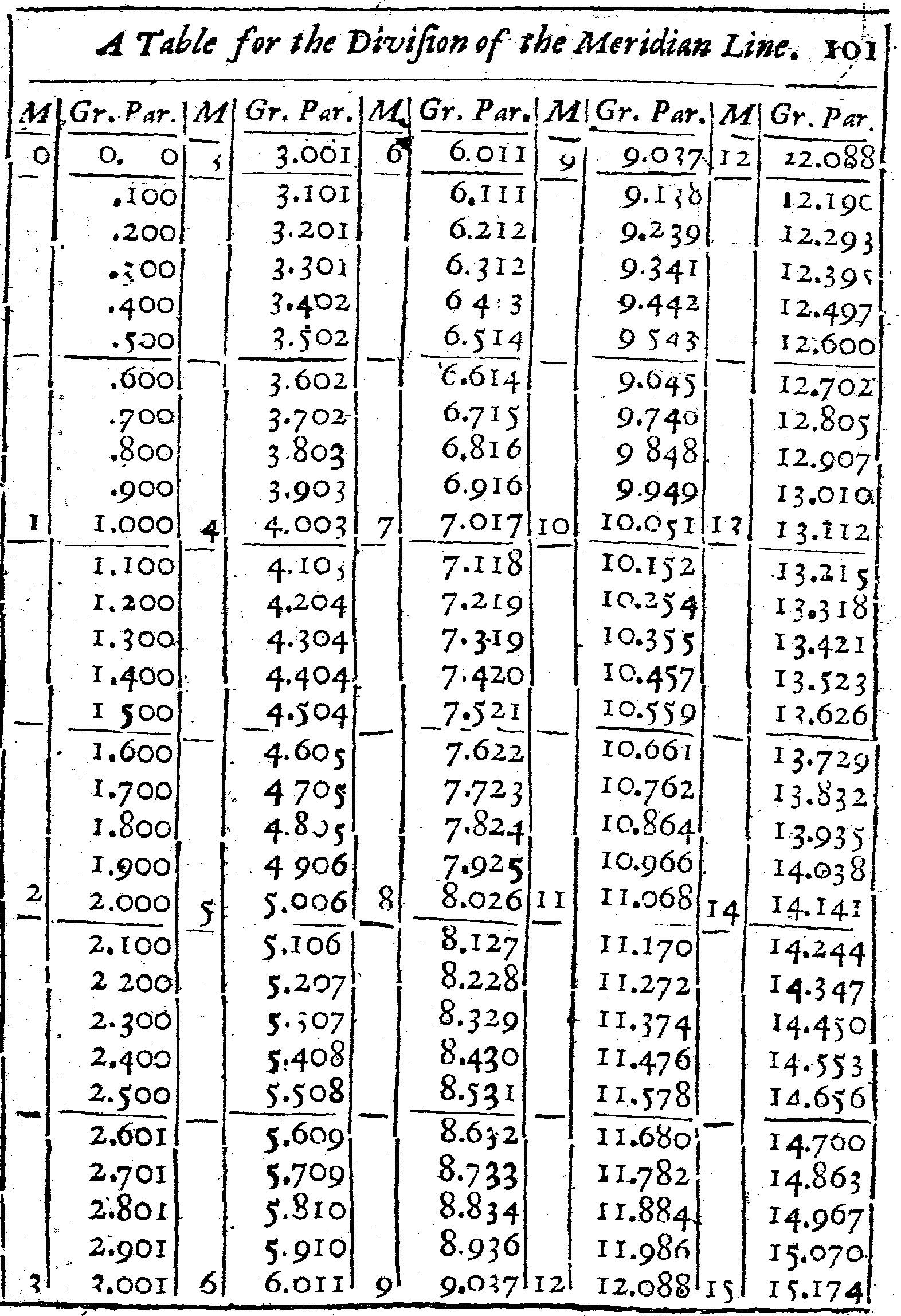
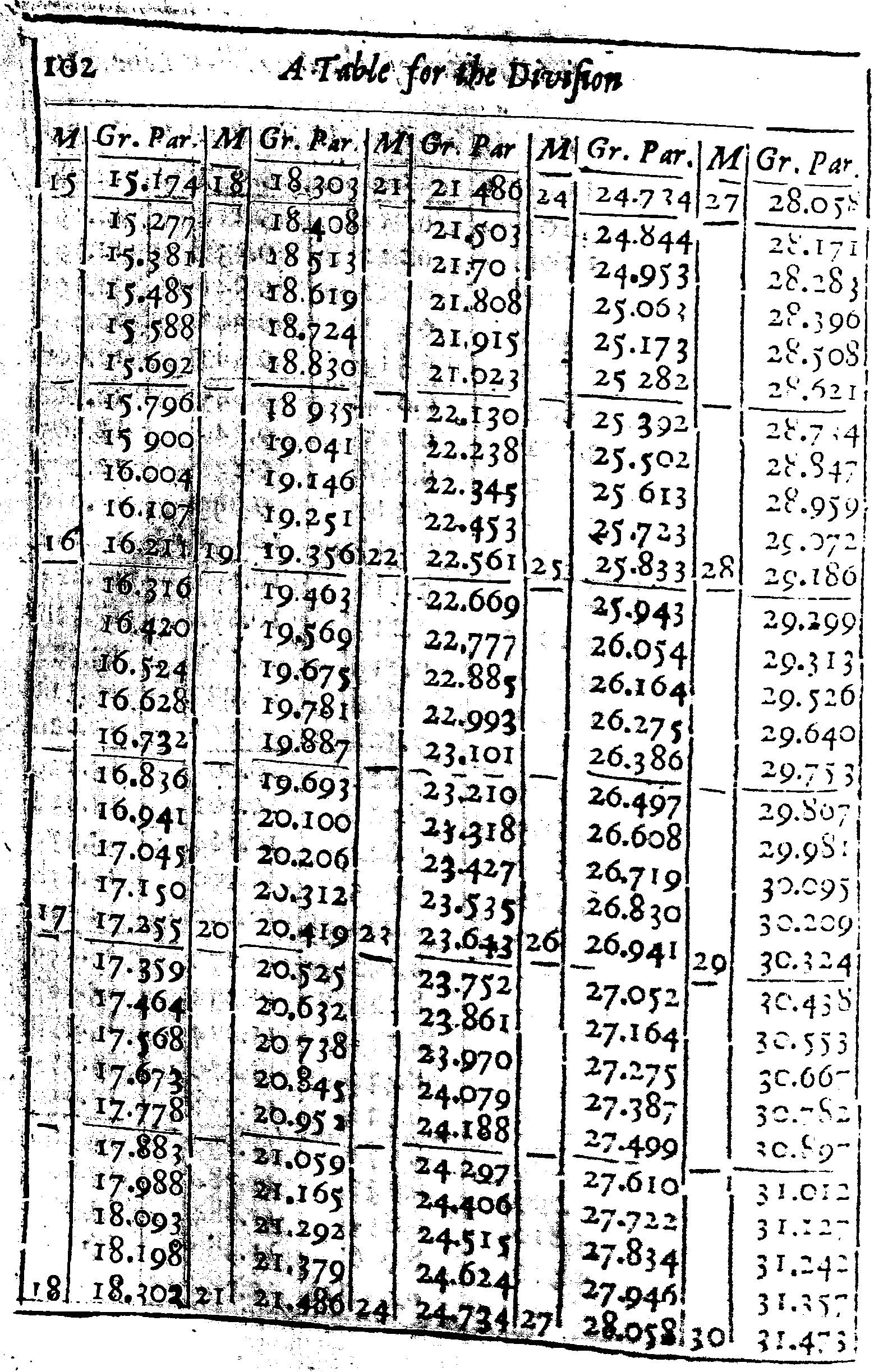
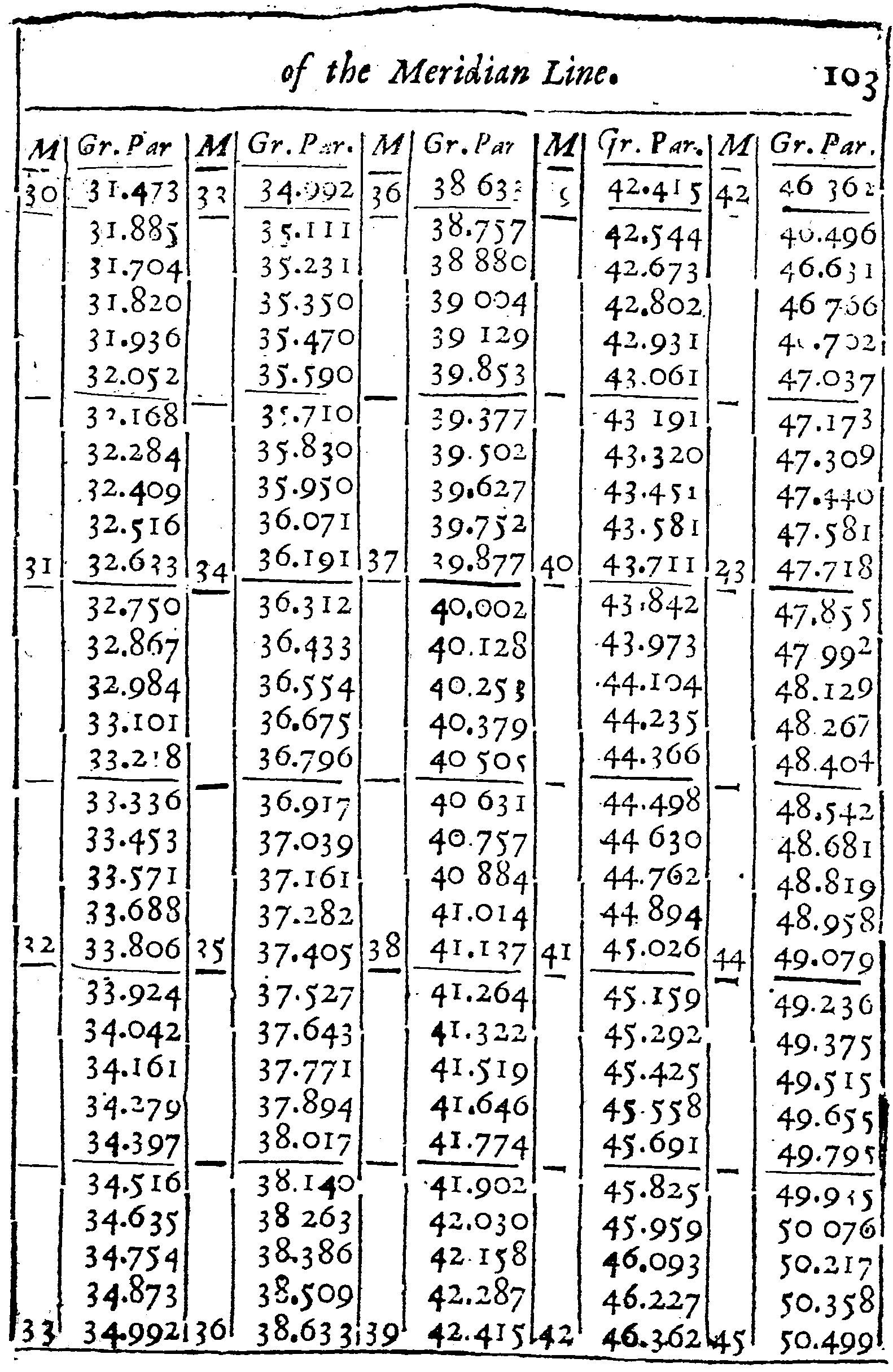
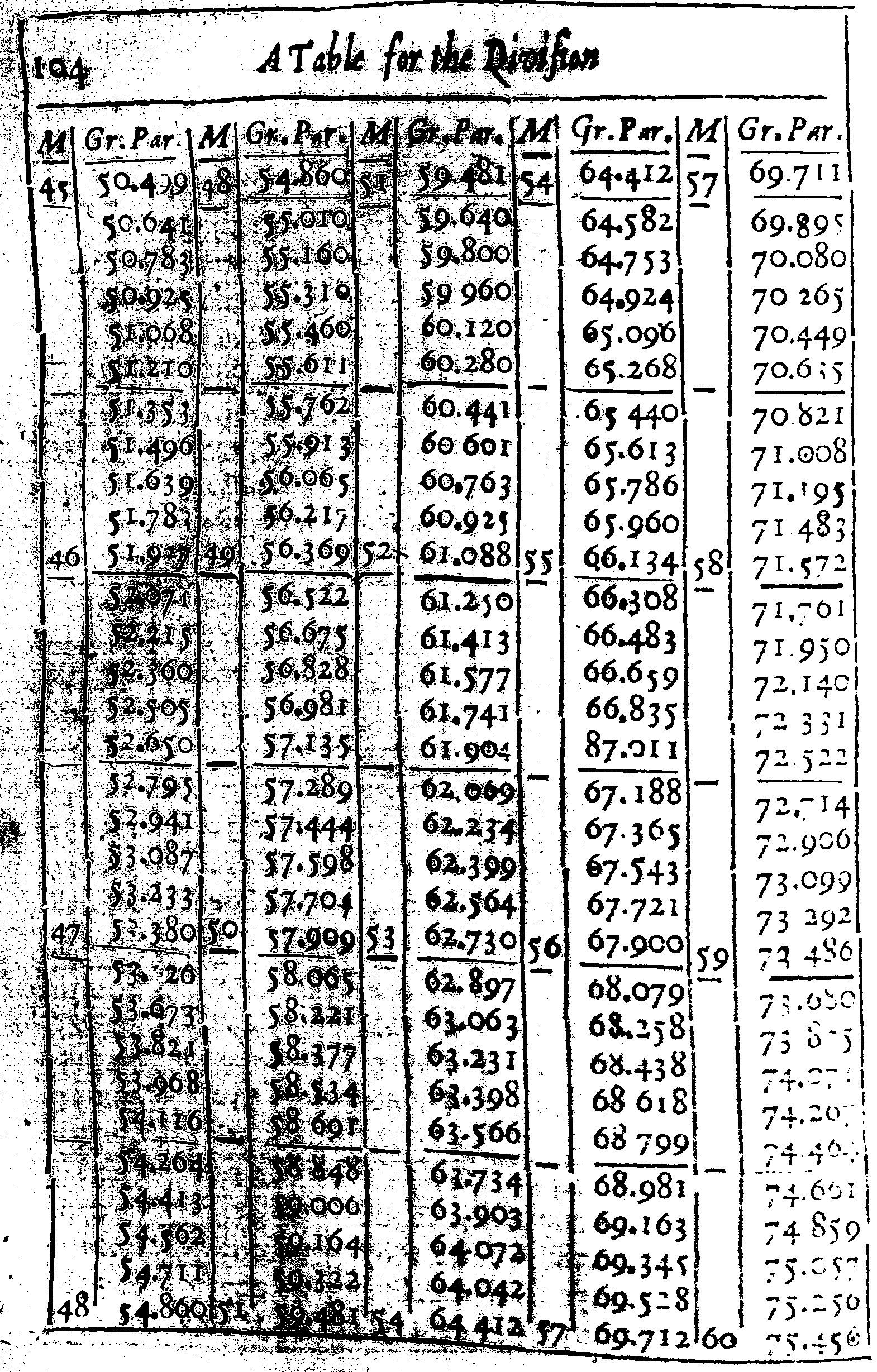
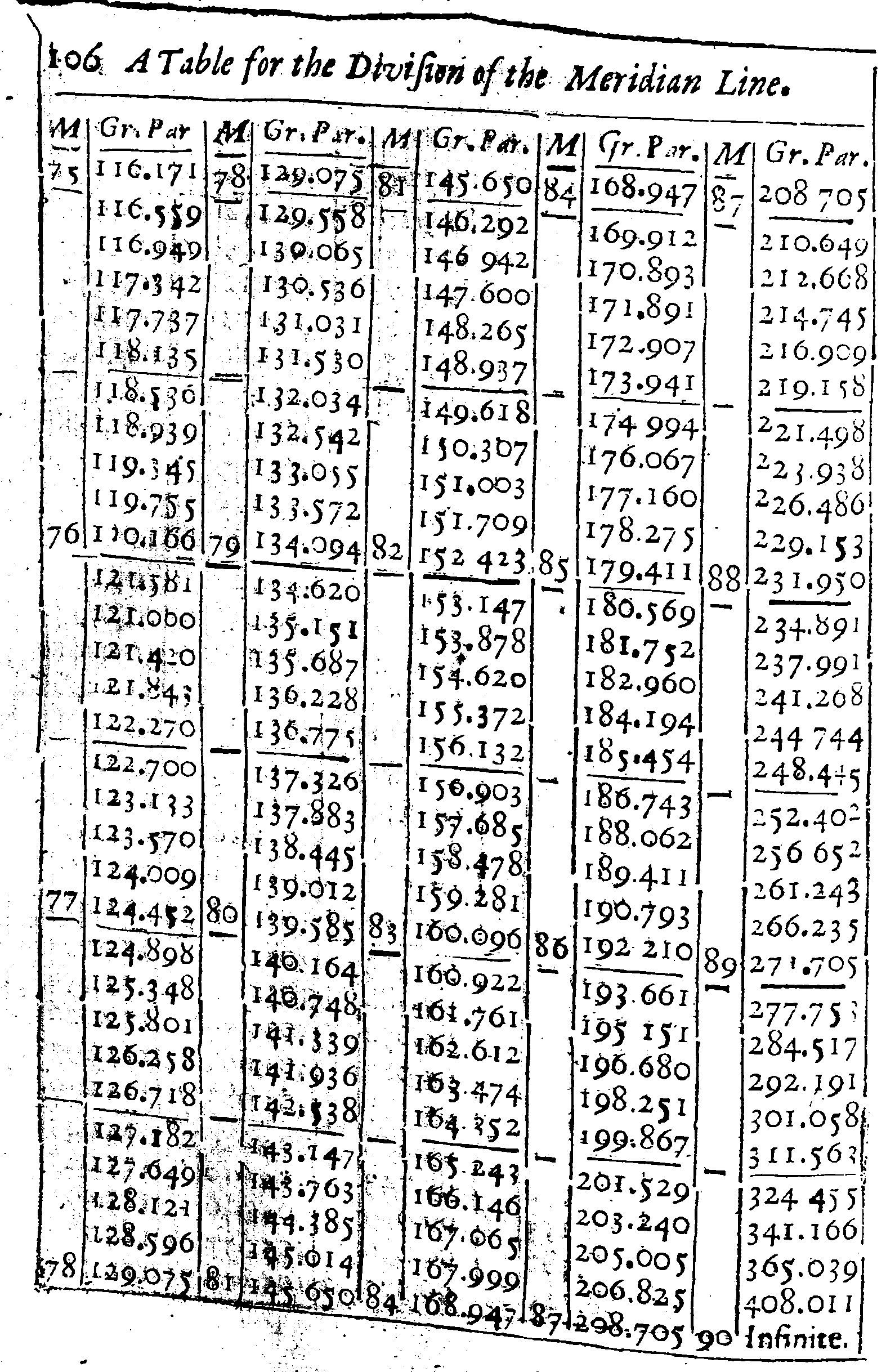
But to avoid error, I have here set down a Table, whereby the Meridian Line may be divided out of the degrees of the Equator supposing each degree in the Equator, to be subdivided into a thousand parts. By which Table, and the usual Table of Sines, Tangents, and Secants, the Proportions following may be also resolved Arithmetically, For the manner of division, let the Equator be drawn, and divided, and crossed with Parallel Meridians, as in the common Sea-chart: then look into the Table, and let the distance between the Equator and 40 gr. in the Meridian, from the Equator, be equal to 43 gr. 711 parts of the Equator, as in the Table: let 50 gr. in the Meridian from the Equator, be equal to 57 gr. 909 parts of the Equator, and so in the rest.
The making of this Table is, by addition of secants. For the Parallels of latitudes being less than the Equator or meridian in such proportion as the Radius is to the Secant of the Parallel. For example, the Parallel of 60 degrees of latitude is less than the Equator (and consequently, each degree of this Parallel of 60 degrees less than a degree of the Equator, or Meridian) in such proportion as 100000 the Radius, hath unto 200000 the Secant of 60 degrees.
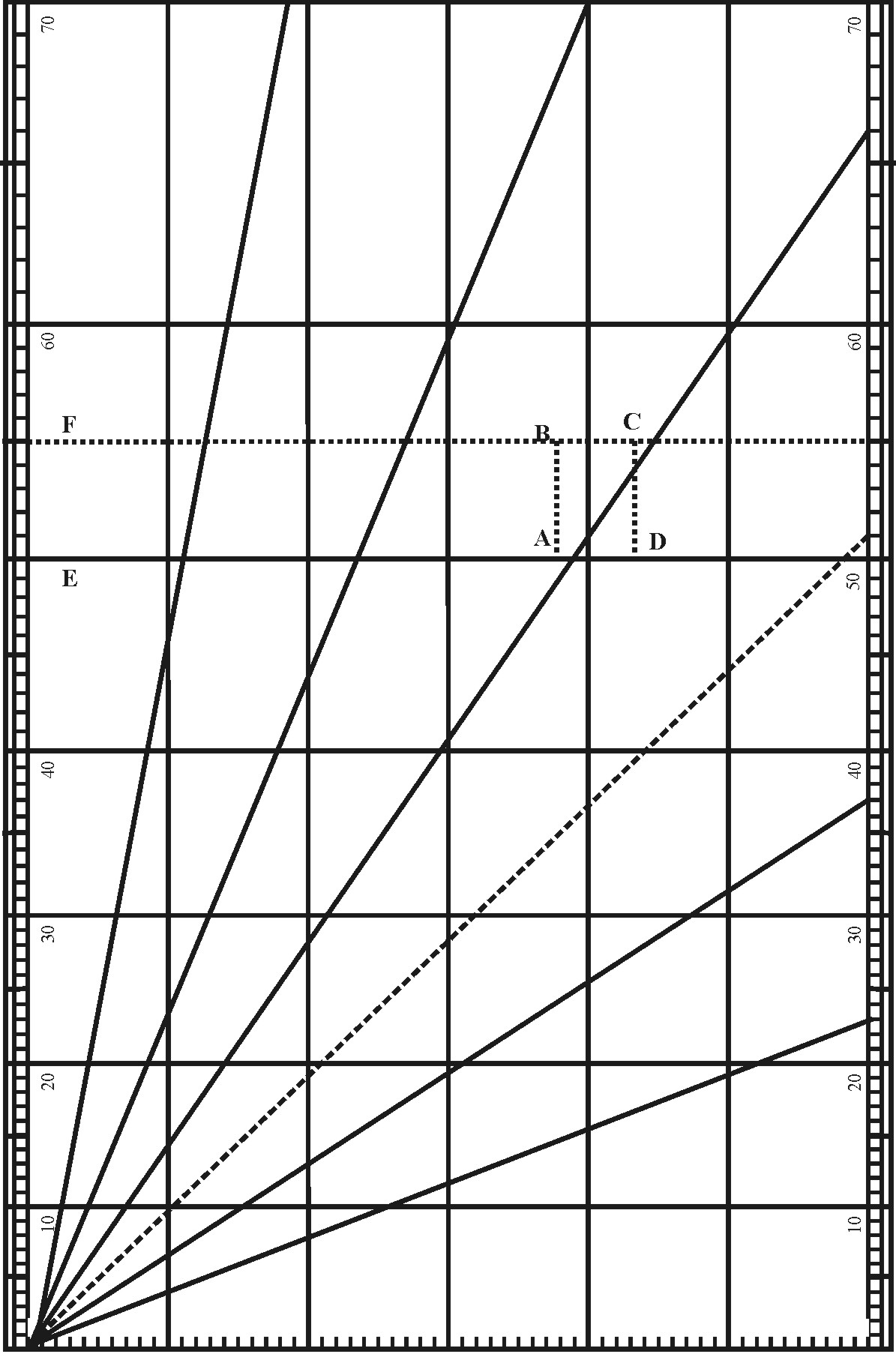
If it be a particular Chart, I would first draw the Line AB serving for the first Meridian, and cross it with two perpendiculars BC and AD, the one at the upper end, the other at the lower end of the Chart, which may serve for the extreme Parallels of Latitude that you are to make use of.
Then considering at what latitude the Chart is to begin and to end, and that this Chart intended for the Latitude of these parts, is to begin at 50 gr. and so end at 55 gr. I look into the table, and find that 50 gr. of Latitude must be drawn at 57 gr. 909 parts, and 55 gr. of Latitude at 66 gr. 134 parts from the Equator; and that the Meridian distance between the parallel of 50 gr. and 55 gr. of latitude must be equal to 8 gr. 225 parts of the Equator. Whereupon I take the Line AB out of the Meridian Line, and diminish it in such proportions as 8.225 hath unto 1000 per 3 Prop. Lin. and with that extent of the Compasses, I divide the two extreme Parallels of latitude into equal degrees, and through each degree draw Meridian Lines parallel to the first Meridian, noting them with 1, 2, 3, 4, &C. and then, I subdivide either one or all of those degrees into ten parts, and (if I may) each tenth part into ten parts more, but howsoever, I suppose each degree to be subdivided into 1000 parts.
The Meridians being drawn, I come to the Parallels of Latitude, beginning at 50 gr.
And finding in the Table, that the distance between the Equator and 50 gr. in the Meridian should be equal to 57 gr. 909 parts in the Equator and his Parallels, I may suppose the lowest Parallel to be 57 gr from the Equator: so the distance between this lowest Parallel and the Parallel of 50 gr. will be only 909 parts. Wherefore I take these 909 odd parts, out of the degrees that I divided before, and prick them down into the two uttermost Meridians from the lowest Parallel upwards, and there draw the Parallel of 50 gr. of latitude.
In like manner, because I find by the table that the distance between the Equator and 51 gr. in the Meridian is 59 gr. 881 parts of the Equator, I abate the former 57 gr. and there remain 2 gr. 481 parts for the distance between the lowest Parallel, and this Parallel of 51: wherefore I take these 2 degrees 481 parts out of the Line before divided, and prick them down in the two uttermost Meridians (as before) from the lowest Parallel upward, and there draw the parallel of 51 degrees of Latitude.
If any desire to have his Chart agree with his Sector, he may make each degree of Longitude equal to the tenth parts of the Line of Lines, and divide the Meridian of his Chart out of the Sector: so shall each degree of the Charts be ten times as large as the like degree on the Sector, and the work be easie from the one to the other.
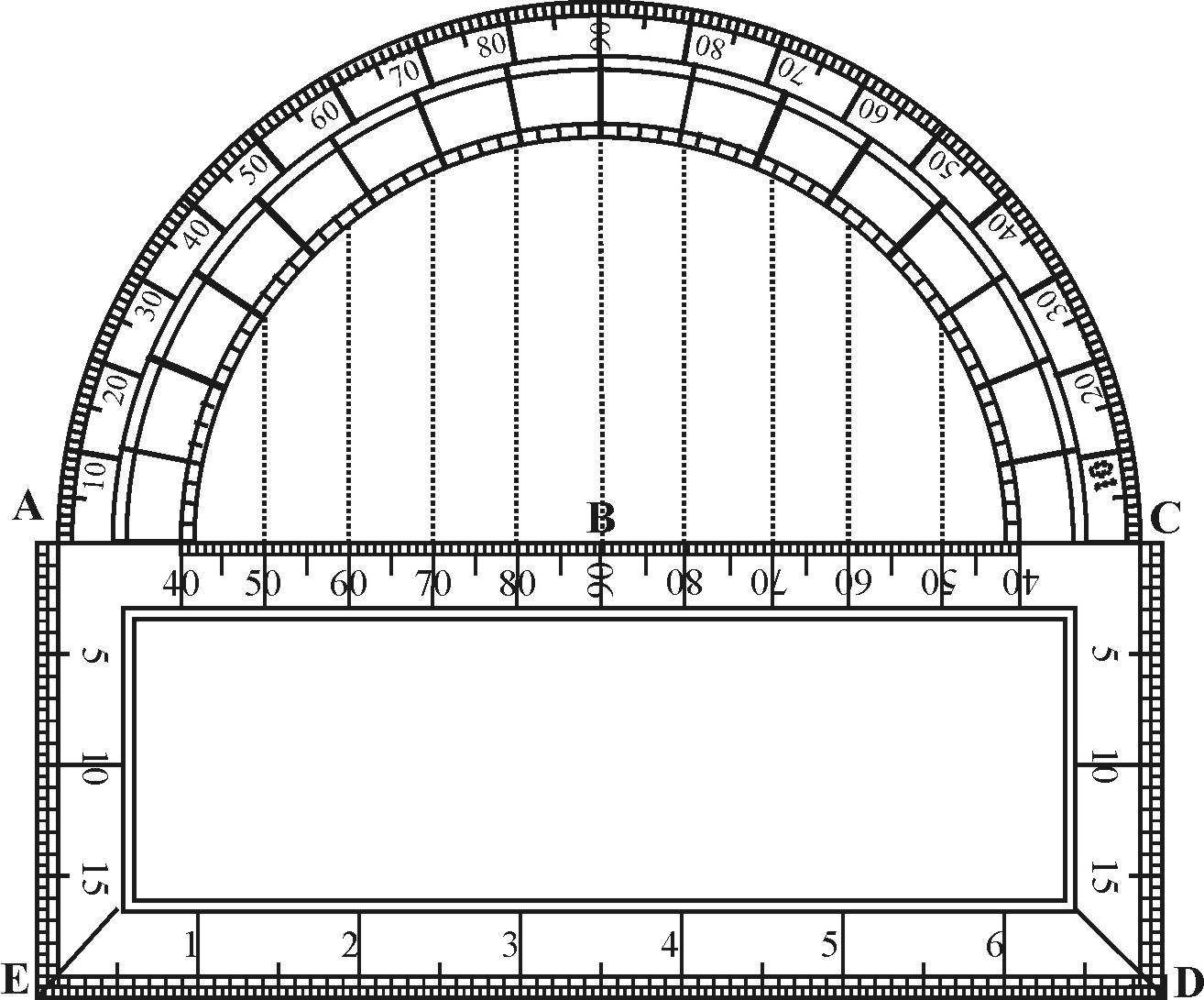
The Lines CD, DE, EA, divided equally according to the Line of Lines upon the Sector, or the Parallels upon the Chart. Only the Diameter AC would be divided unequally, by letting down occule perpendicular Lines upon it from each Degree in the Semicircle, which being done, the intermediate part between the Rumbs and the Diameter may be all cut forth: And the back side of the long Square may be filled with 6 Lines of Chords, or Scales of several parts in the Inch.
So may the Meridian be divided by the parts of the Side ED, the Angles of each Rumb may readily be pricked down by the Degrees in the Semicircle, and the Line of Chords and the other Scales may serve to do the like with more variety.
2. To find how many Leagues answer to one Degree of Longitude in every several latitude.
In sailing by the Compass, the Course holds sometime upon a Great Circle, sometime upon a parallel to the Equator; but most commonly upon crooked Lines, winding towards one of the Poles, which Lines are well known by the Name of Rumbs.
If the Course hold upon a Great Circle, it is either North or South under some Meridian, or East or West under the Equator. And in these cases, every Degree requires an allowance of twenty Leagues; every twenty Leagues will make a Degree difference in the sailing: so that here needs no further Precept than the Rule of Proportion in the Chapter of Lines.
But if the Course hold East or West, or nay of the Parallels to the Equator,
- As the Radius, is to twenty Leagues, the Measure of one Degree at the Equator:
- So the Sine of the Complement of the Latitude, to the Measure of leagues answering to one Degree in that Latitude.
Wherefore I take 20 Leagues out of the Line of Lines, and make it a parallel radius, by fitting it over in the Sines of 90 and 90: so his parallel Sine taken out of the Complement of the latitude, and measured in the Line of Lines, shall shew the number of Leagues required.
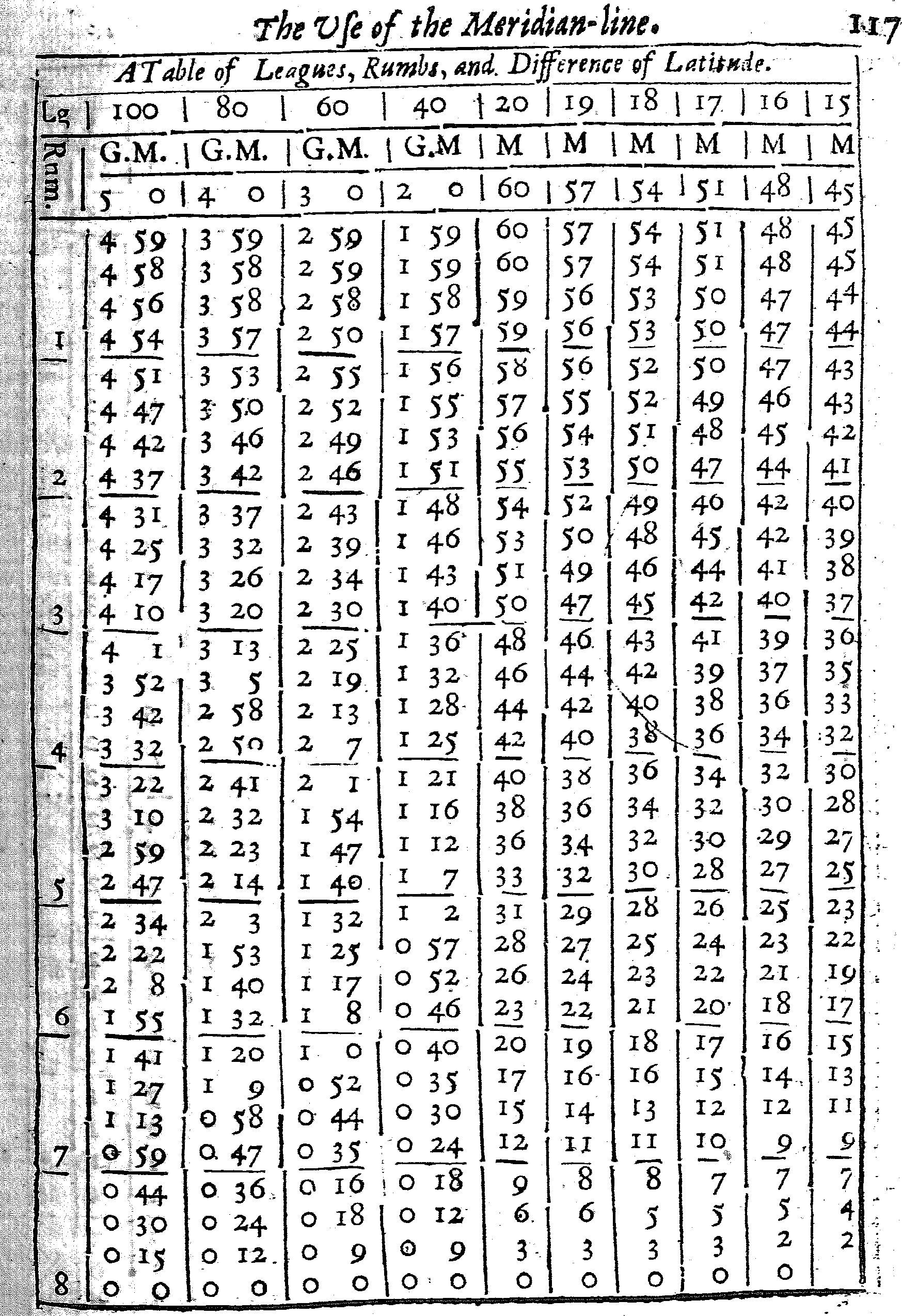
Thus in the Latitude of 18 gr. 12 m. we shall find 19 Leagues answering to one Degree of Longitude, and 18 Leagues in the Latitude of 25 gr. 15 m. as in this Table.
| Gr. | m. | Leag. |
| 0 | 0 | 20 |
| 18 | 12 | 19 |
| 25 | 15 | 18 |
| 31 | 48 | 17 |
| 36 | 52 | 16 |
| 41 | 25 | 15 |
| 45 | 34 | 14 |
| 49 | 28 | 13 |
| 53 | 8 | 12 |
| 56 | 38 | 11 |
| 60 | 0 | 10 |
| 63 | 15 | 9 |
| 66 | 25 | 8 |
| 69 | 30 | 7 |
| 72 | 32 | 6 |
| 75 | 31 | 5 |
| 78 | 28 | 4 |
| 81 | 23 | 3 |
| 84 | 15 | 2 |
| 87 | 8 | 1 |
This may be done more readily without opening the Sector, by doubling the Sine of the Complement of the Latitude, as may appear in the same Example.
It may also be done more readily by the Line of Meridians, either upon the sector, or upon the Chart: For if we open a pair of Compasses to the quantity of one Degree of Longitude in the Equator, or one of his Parallels, and measure it in the Meridian Line, setting one Foot as much above the latitude given, as the other falleth beneath it, so that the Latitude may be in the middle between the Feet of the Compasses, the number of Leagues intercepted shall be that which was required.
But if the Course hold upon any of the Rumbs, between a Parallel of the Equator and the Meridian, we are to consider (besides the Equator of the World to which we tend, which must be always known).
- The difference of Longitude, at least in general.
- The difference of latitude, and that in particular.
- The Rumb whereon the Course holds.
- The distance upon the Rumb, which is the distance which we are here to consider, and is always somewhat greater than the like distance upon a greater Circle. And for these, first, I shew in general this third Proposition.
3. To find how many Leagues do answer to one Degree of latitude in every several Rumb.
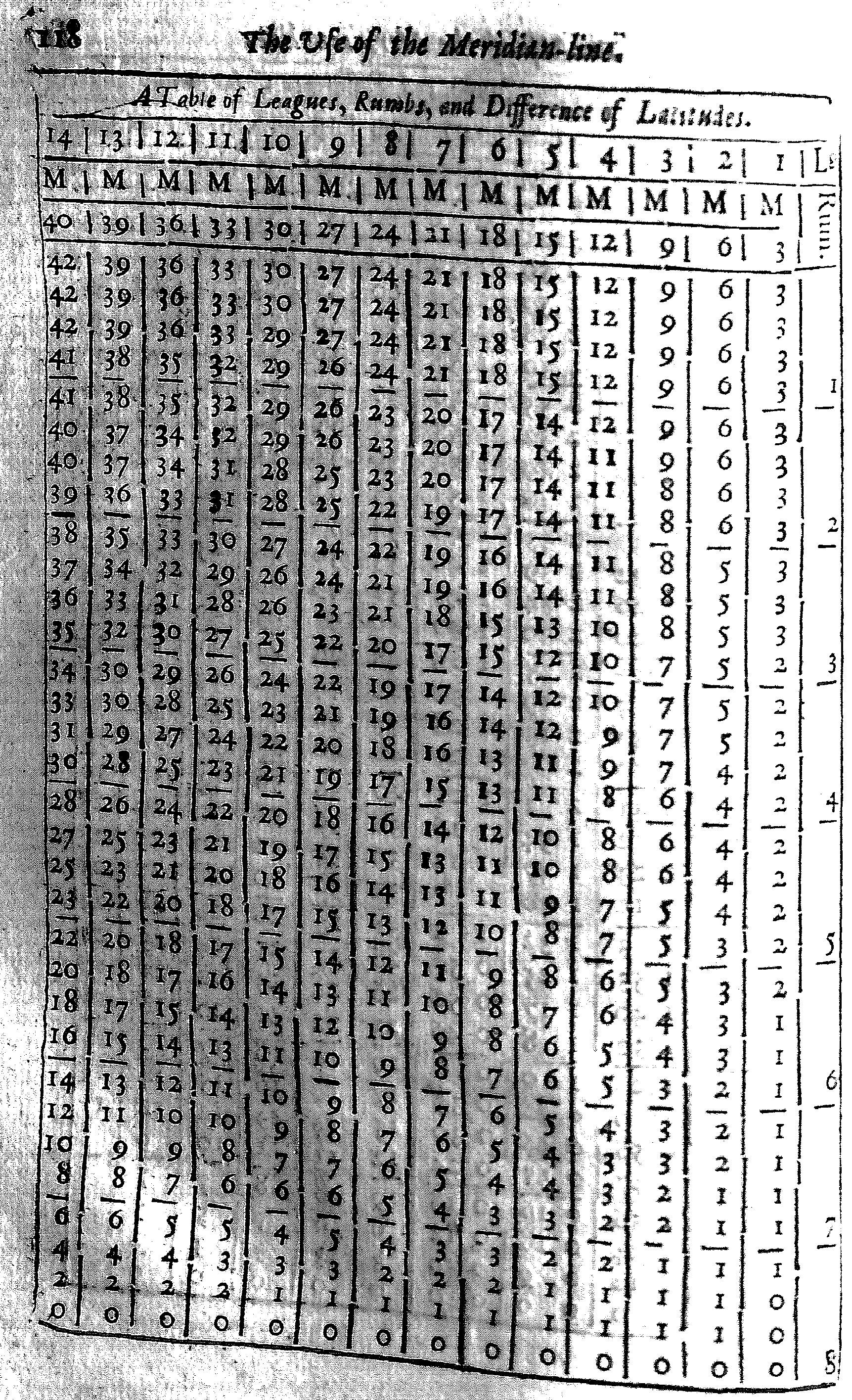
The Seamans Compass is commonly divided into 32 Points; the half, into 16; the quarter, into 8; which have their names of NNbE, NNE, &C. according to those parts of the World to which they point. Answerable to these Points, are the Rumbs upon their Chart; each quarter divided into 8, each Rumb 11 gr. 15 m. distant one from the other: The first Rumb being that which is 11 gr. 15 m. distant from the Meridian; the second, 22 gr. 30 m. the third, 33 gr. 45 m. and so the rest. And (if they have need of smaller parts) they subdivide each Rumb into quarters, allowing 2 gr. 48 m. to the first quarter, 5 gr. 37 m. to the half Rumb, &c. as in the Table following.
| Rumbs | Incinat. to the Merid. | Number of Leagues | ||
| Gr. | M. | Lgs. | Par. | |
| 1 | 2 | 49 | 20 | 02 |
| 5 | 37 | 20 | 10 | |
| 8 | 26 | 20 | 22 | |
| 11 | 15 | 20 | 39 | |
| 2 | 14 | 4 | 20 | 62 |
| 16 | 52 | 20 | 90 | |
| 19 | 41 | 21 | 24 | |
| 22 | 30 | 21 | 65 | |
| 3 | 25 | 19 | 22 | 12 |
| 28 | 7 | 22 | 68 | |
| 30 | 56 | 23 | 32 | |
| 33 | 45 | 24 | 05 | |
| 4 | 36 | 34 | 24 | 90 |
| 39 | 22 | 25 | 87 | |
| 42 | 11 | 26 | 99 | |
| 45 | 0 | 28 | 8 | |
| 5 | 47 | 49 | 29 | 78 |
| 50 | 37 | 31 | 52 | |
| 53 | 26 | 33 | 57 | |
| 56 | 15 | 36 | 00 | |
| 6 | 52 | 4 | 38 | 90 |
| 61 | 52 | 42 | 43 | |
| 64 | 41 | 46 | 78 | |
| 67 | 30 | 52 | 26 | |
| 7 | 70 | 19 | 59 | 37 |
| 73 | 7 | 68 | 90 | |
| 75 | 56 | 82 | 31 | |
| 78 | 45 | 102 | 52 | |
| 8 | 81 | 34 | 136 | 30 |
| 84 | 2 | 205 | 24 | |
| 87 | 11 | 407 | 60 | |
| 90 | 0 | Infinita. | ||
- As the Sine of the Complement of the Rumb from the Meridian, is to 20 Leagues, the Measure of one Degree of the Meridian:
- So is the Radius, to the Leagues answering to one Degree upon the Rumb.
As if in sailing NEbN, from 50 gr. North Latitude, it were required how many Leagues the Ship should run before it could come to 51 gr. of latitude, because this is the third Rumb, and the Inclination thereof 33 gr. 45 m. I would take 20 Leagues, &c.
Wherefore I take 20 Leagues out of the Line of Lines, and make it a parallel Sine of 56 gr. 15 m. the Complement of the Rumb from the Meridian; so his parallel Radius taken and measured in the Line of Lines, shall shew me 24 for the number of Leagues required.
And thus in the first Rumb from the Meridian we shall find 20 Leagues 39 parts answering to one Degree of latitude, and 21 Leagues 65 parts in the second Rumb, &c. as in the Table, where we subdivide each League into a hundred parts, and shew besides what Inclination the Rumb hath to the Meridian.
This may be done more readily without opening the Sector, by doubling the Secant of the Rumb, as may appear in the same Example.
It may also be one upon the Chart, if first we draw the Rumb; then we take the distance upon the Rumb between two parallels, and measure it in the Meridian-line, as far above the greater Latitude as beneath the lesser. For the number of Leagues intercepted shall be that which was required.
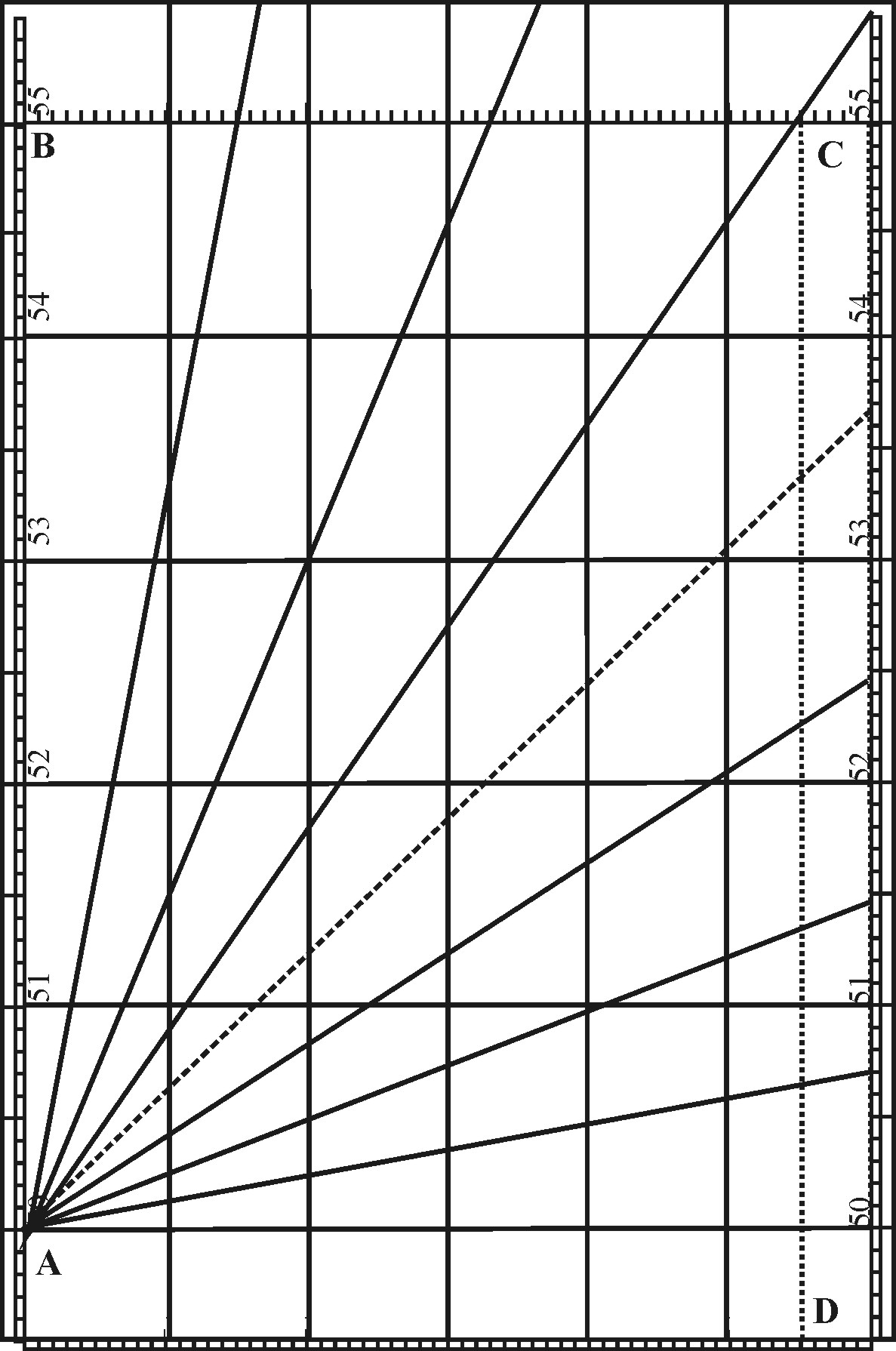
For Example: In the second Chart, pag. 113. I first draw the 8 Rumbs, from the Intersection of the meridian with the parallel of 50 gr. of Latitude, either by that which I have shewed before in the general Use of Sines, Chap. II. Prop. 10. or by help of the Protraction last mentioned: For, laying the Center of the Protractor to the Point of Intersection (which is to be the Center of the Rumbs) and turning the Diameter of the Protractor until it be parallel to the Meridians of the Chart (which is then done, when the Meridians and Parallels in the Chart fall under like divisions in the Protractor) I may make one prick at 11 gr. 15 m. another at 22 gr. 30 m. in the outward part of the Semicircle; and so the rest.
Or, having neither Sector nor Protractor, I would have a Line of Chords set on the side of the Ruler which I am to use, from which I may take 60 gr. and with that extent setting one Foot of the Compasses in the former Point of Intersection, draw an occult Ark of a Circle, and therein prick down the former Arks from the Meridian, as in Chap. 11. Prop. 10. So these Arks being pricked down by either of these ways, the Right Lines drawn through the Center and those pricks, shall be the Rumbs required.
The Rumbs being drawn, I take the distance between the Parallels of 50 and 51 gr. upon AC, the third Rumb; and measuring it in the Meridian-line, I find the Compasses to reach from above 1/10 of a Degree below the Parallel of 50, but 1/10 above the Parallel of 51 gr. intercepting 1 gr. 2/10 or 24 Leagues, such as 20 make a degree.

Again, I take the distance upon the same Rumb between the Parallel of 54 and 55 gr. which I find to be somewhat longer than the former distance between the Parallels of 50 and 51; but measuring it in the Meridian Line, according to the Latitude of the Parallel, I find but 1 gr. 2/10 (or 24 Leagues) as before, for the number of Leagues answering to 1 Degree of Latitude upon this third Rumb.
And by the same reason, I may find the number of Leagues answering to a Degree of Latitude upon the rest of the Rumbs agreeable to the Table.
This considered in general, I shew more particularly in twelve Propositions following, how of these four any two being given, the other two may be found, both by Mercator's Chart, and by this Sector.
1. By one Latitude, Rumb, and Distance, to find the Difference of Latitudes.
- As the Radius, to the Sine of the Complement of the Rumb from the Meridian:
- So the Distance upon the Rumb, to the difference of Latitudes.
Let the Place given be A, in the Latitude of 50 gr. C in a greater latitude, but unknown, the distance upon the Rumb being 6 gr. between them, and the Rumb the third from the Meridian.
First, I take 6 gr. from the distance upon the Rumb, out of the Line of Lines, and make it a Parallel Radius, by putting it over in the Sines of 90 and 90: then keeping the Sector at this Angle, I take out the parallel Sine of 56 gr. 15 m. which is the Sine of the Complement of the third Rumb from the Meridian, and measuring it in the Line of Lines, I find it to be 5 gr. and such is the difference of Latitude required.
Or, I may take out the Sine of 56 gr. 15 m. for the Complement of the third Rumb from the Meridian, and make it a parallel Radius, then keeping the Sector at this Angle, I take 6 gr. for the distance, either out of the Line of Lines, or any other Scale of Equal parts, or else out of the Meridian Line, and lay it on both sides of the Sector from the Center, either on the Line of Lines or Sines; so the parallel taken from the Terms of this distance, and measured in the same Scale wherein the distance was measured, shall shew the difference of Latitude to be 5 gr. as before.
But in shorter distance, such as fall within the compass of the days sailing, this Work will hold much better; as may appear by comparing the Work with the table following, where the Numbers in the front do signify the Leagues; those in the side, the Rumb; and the rest in the middle, the difference of Latitude.
In the Chart let a Meridian AB be drawn through A, and in A with AB make an Angle of the Rumb BAC: Then open the Compasses, according to the latitude of the Place, to EF the quantity of 6 gr. in the Meridian, transferring them into the Rumb from A to C, and through C draw the parallel BC, crossing the Meridian AB in B: so the Degrees in the Meridian from A to B shall shew the difference of Latitude to be 5 gr.
2. By the Rumb and both Latitudes to find the Distance upon the Rumb.
- As the Sine of the Complement of the Rumb from the Meridian, is to the Radius:
- So is the Difference of latitudes, to the Distance upon the Rumb.
As is the Places given were A in the Latitude of 50 gr. C in the latitude of 55 gr. and the Rumb the third from the Meridian.
Here I may take 5 gr. for the difference of Latitude out of the Line of Lines, and put it over in the Sine of 56 gr. 15 m. for the Complement of the third Rumb from the Meridian. Then keeping the Sector at this Angle, I take out the Parallel Radius, and measure it in the Line of Lines: I find it to be 6 gr. and such is the distance upon the Rumb, which was required.
Or I may take the lateral Radius, and make it a Parallel Sine of 56 gr. 15 m. the Complement of the Rumb from the Meridian: then keeping the Sector at this Angle, I take 5 gr. for the difference of Latitudes, either out of the Line of Lines, or out of some other Scale of equal parts, and lay it on both sides of the Sector from the Center, either on the Line of Lines, or of Sines: so the Parallel taken from the Terms of this difference, and measured in the same Scale with the difference, shall shew the distance upon the Rumb to be 6 gr. or 120 Leagues.
Or keeping the Sector at this Angle, I may take the difference between 50 gr. and 55 gr. out of the Meridian Line, and measuring it in the Equator, I shall find it to be equal to 8 gr. 22 p. of the Euqator. Wherefore I take the Parallel between 822 and 822 out of the Line of Lines, and measuring it in the Line of Lines, I shall find it to be 989; which shews that according to this projection, the distance upon this third Rumb, answerable to the former difference of Latitudes, will be equal to 9 gr. 89 p. of the Equator.
Or the Sector remaining at this Angle, I may take the difference between 50 gr. and 55 gr. out of the Meridian Line, and lay it from the Center on both sides of the Sector, either in the Line of Lines or of Sines: so the Parallel taken from the terms of this difference, shall be the very Line of distance required, the same with AC or EF upon the Chart; which may serve for the better pricking down of the distance upon the Rumb, without taking it forth of the Meridian Line, as in the former Proposition.
Or if the Rumb fall nearer to the Equator, that the lateral Radius cannot be fitted over it, this Proposition may be wrought by Parallel entrance.
For, if I first take out the Sine of 56 gr. 15 m. and make it a parallel Radius, by fitting it over in the Sines of 90 and 90, or in the ends of the Line of Lines, and then take 5 gr. For the difference of latitudes out of the Line of Lines, and carry it parallel to the former, I shall find it to cross both Line of Lines in the Point of 6: and so it gives the same distance as before.
Or if the distance be small, it may be found by the former Table. For the Rumb being found in the side of the Table, and the difference of Latitude in the same Line; the top of the Column wherein the difference of Latitude was found, shall give the number of Leagues in the distance required.
Or we may find this distance in the table of Rumbs in the fifth Proposition following. For according to the example, look into the Table of the third Rumb for 5 gr. Of Latitude, and there we shall find 6 gr. 10 parts under the title of distance.
So if the difference of Latitude upon the same Rumb ware 50 gr. The distance would be 60 gr. 13 parts. If the difference of Latitude upon the same Rumb were only ½ of a drgeree, the distance would be only 60 parts, such as 100 do make a degree.
In the Chart let a Meridian AB be drawn through A, and Parallels of Latitude through A and C; and then in A, with AB, make an Angle of the Rumb BAC: so the distance take from A to C, and measured in the Meridian Line, according to the Latitude of the places, shall be found to be 6 gr. Or 120 Leagues. And such is the distance required.
3. By the distance and both Latitudes, to find the Rumb.
- As the distance upon the Rumb, to the difference of Latitudes:
- So the Radius, to the Sine of the Complement of the Rumb from the Meridian.
As if the places given were A, in the Latitude of 50 gr. C in the latitude of 55 gr. The distance between them being 6 gr. Upon the Rumb. First I take 6 gr. For the distance upon the Rumb, and lay it on both sides of the Sector from the Center; then out of the same Scale I take 5 gr. For the difference of Latitude, and to it open the Sector in the terms of the former distance: so the parallel Radius taken and measured in the Sines, doth give 56 gr. 15 m. the Complement whereof 33 gr. 45 m. is the Angle of the Rumbs inclination to the Meridian, which was required.
In the Chart let a Meridian AB be drawn through A, and Parallels of Latitude, both through A and C; then open the Compasses according to the latitude of the places to, the quantity of 6 gr. In the Meridian, and setting one foot in A, turn the other till it crosses the Parallel BC in C, and draw the right Line AC: so the Angle BAC shall shew the inclination of the Rumb to the Meridian to be 33 gr. 45 m. as before.
These three last Propositions depend one on the other, and may be wrought as truly by te Common Sea-Chart as by this of Mercators Projection: and therefore in working them by the Sector, the distance and the difference of latitudes may as well or better be taken out of the Line of Lines (which here representeth the Equator) or any other Line of equal parts, as out of the inlarged degrees in the Meridian Line. But in the Propositions following, the difference of Longitude must be taken aout of the Equator; the difference of Latitude and distance upon the Rumb must always be taken out of the Meridian Line: which I therefore call the proper difference, and proper distance.
4. By the Longitude and Latitude of two places to find the Rumb.
As if the places given were A, in the latitude of 50 gr. C in the Latitude of 55 gr. And the difference of Longitude between them were 5 gr. 30 m.
In the Chart let Meridians and parallels be drawn through A and C, and a straight Line for the Rumb from A to C; then by that we shewed Chap. 2. Proposition 9. inquire the quantity of the Angle BAC, and it shall be found to be 33 gr. 45 m. which is the third Rumb from the Meridian. Wherefore the proportion holds for the Sector.
- As AB the proper difference of Latitude, is to BC the difference of Longitude:
- So is AB Radius, to BC, the Tangent of the Rumb from the Meridian.
According to this I take the proper difference of latitude from 50 gr. To 55 gr. Out of the Line of Meridians, and lay it on both sides of the Sector from the Center; then I take the difference of Longitude 5 gr. ½ out of the Line of Lines, and to it open the Sector in the terms of the former difference of latitudes, so the Parallel Radius taken from between 90 and 90: and measured in the greater Tangent on the side of the Sector, doth give 33 gr. 45 m. for the Rumb required.
But if the Rumb fall nearer to the Equator;
- As AD the difference of Longitudes, is to DC the proper difference of Latitudes:
- So AD the Radius, to DC the tangent of the Rumb from the Equator.
According to this I take the former difference of Latitudes from 50 gr. To 55 gr. Out of the Line of Meridians, and to it open the Sector in the terms of the difference of Longitude reckoned in the Line of Lines from the Center, so the Parallel Radius taken and measured in the tangent, doth give 56 gr. 15 m. for the Rumb from the Equator: which is the Complement to the former 33 gr. 45 m. and so both ways it is found to be the third Rumb from the Meridian.
But if this Rumb were to be found in the common Sea-chart, it should seem to be above 47 gr. Which is more than the fourth Rumb from the Meridian.
5. By the Rumb and both Latitudes, to find the difference of Longitudes.
As if the places given were A, in the Latitude of 50 gr. and C in the Latitude of 55 gr. and the Rumb the third from the Meridian.
In the Chart, let a Meridian be drawn through A, and a Parallel of latitude through C, then in A, with AB, make the Angle of the Rumb from the Meridian BAC, (as was shewed Cap. 2 Prop. 10.) So the degree in the Parallel between B and C, shall be found to be 5 gr. ½, the difference of Longitude which was required. Wherefore the proportion holds for the Sector,
- As AB the Radius, to BC the Tangent of the Rumb from the Meridian:
- So AB the proper difference of the Latitudes, to BC the difference of Longitude.
According to this we may take the Tangent of the Rumb which is 33 gr. 45 m. from the Meridian, out of the greater tangent on the side of the Sector, and putting it over between 90 and 90, make it a Radius: then keeping the Sector at this Angle, take the proper difference of Latitudes from 50 gr. To 55 gr. Out of the Line of Meridians, and lay it on both sides of the Sector from the Center: so the parallel taken from the terms of this difference, and measured in the Line of Lines, shall shew the difference of Longitude to be 5 gr. ½.
- As DC the Tangent of the Rumb from the Equator, to AD the Radius:
- So CD the proper difference of the latitudes, to AD the difference of Longitude.
According to this, we may best work by Parallel entrance, first taking 56 gr. 15 m. for the Angle of the Rumb from the Equator, out of the greater Tangent, and make it a Parallel Radius: then take the proper difference of latitudes out of the Line of Meridians, and carry it Parallel to the former: so we shall find it to cross the Line of Lines in 5 gr. ½. And this is the difference of Longitude required, the same as before.
But if this difference were to be found by the common Sea-chart, it should seem to be only 3 gr. 20 m., which is more than two degrees less than the truth. And yet this error would be greater, if either the latitude be greater, or the Rumb fall nearer the Equator, as may appear by comparing the common Sea-chart with the Table following.
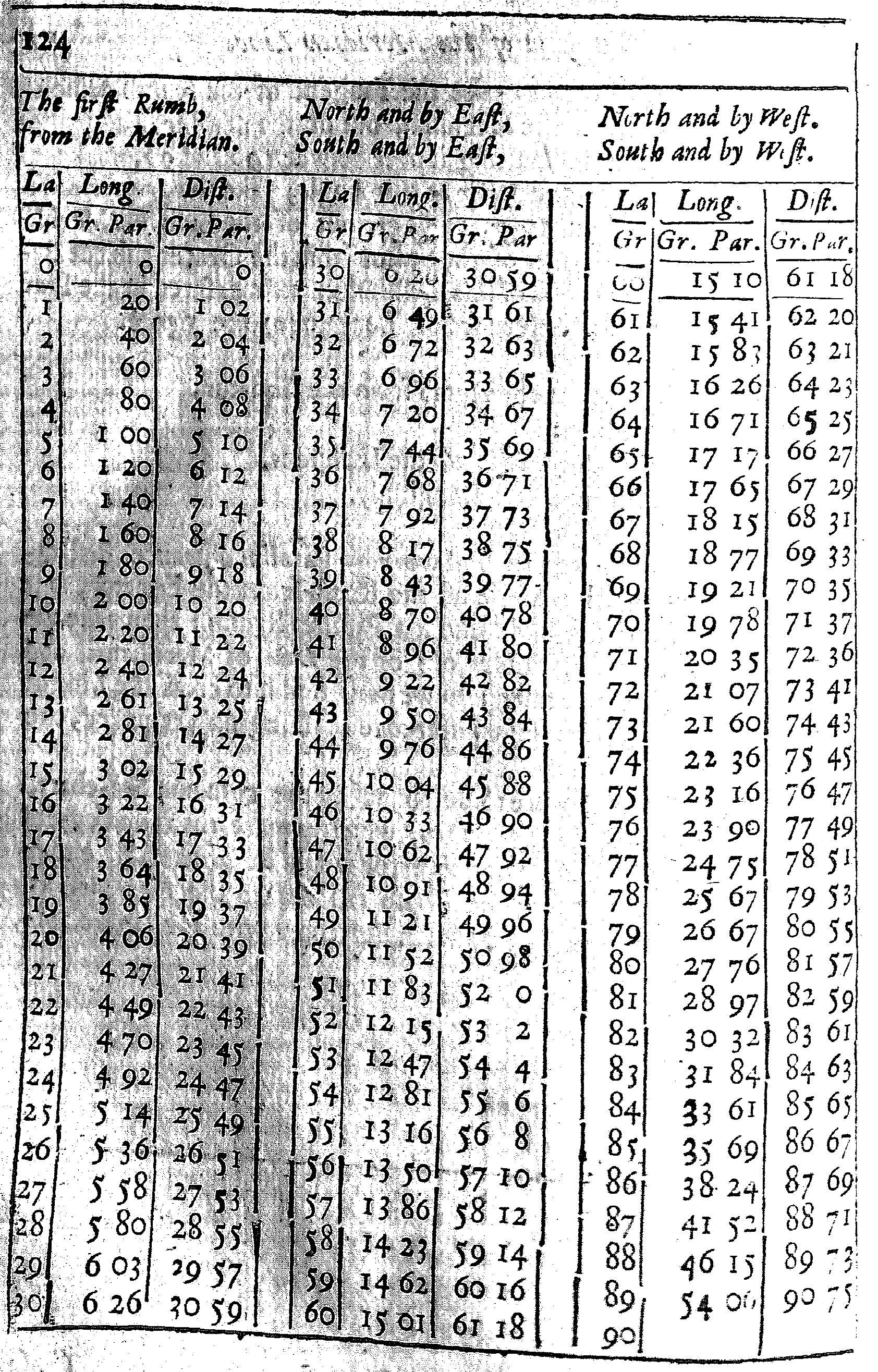
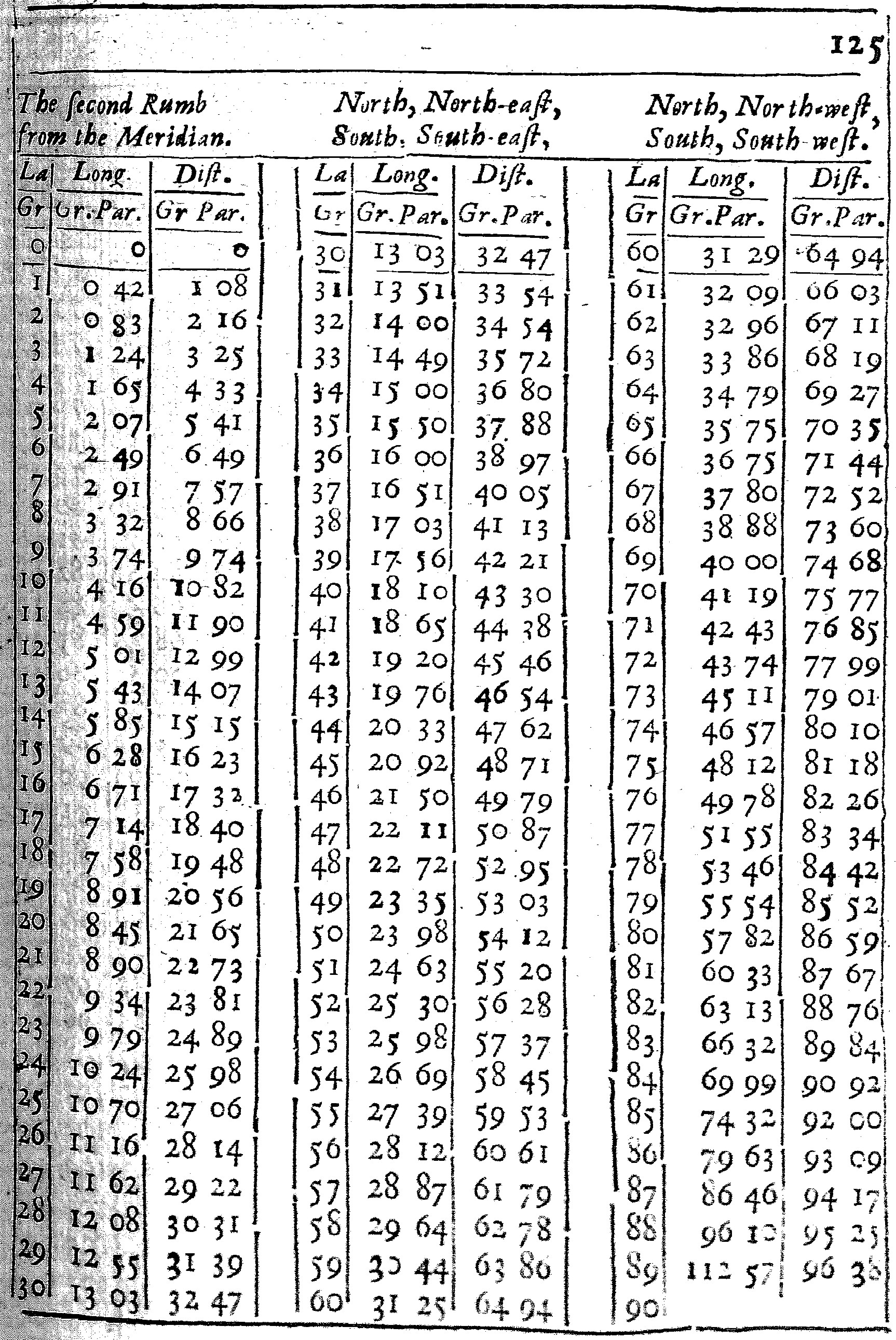
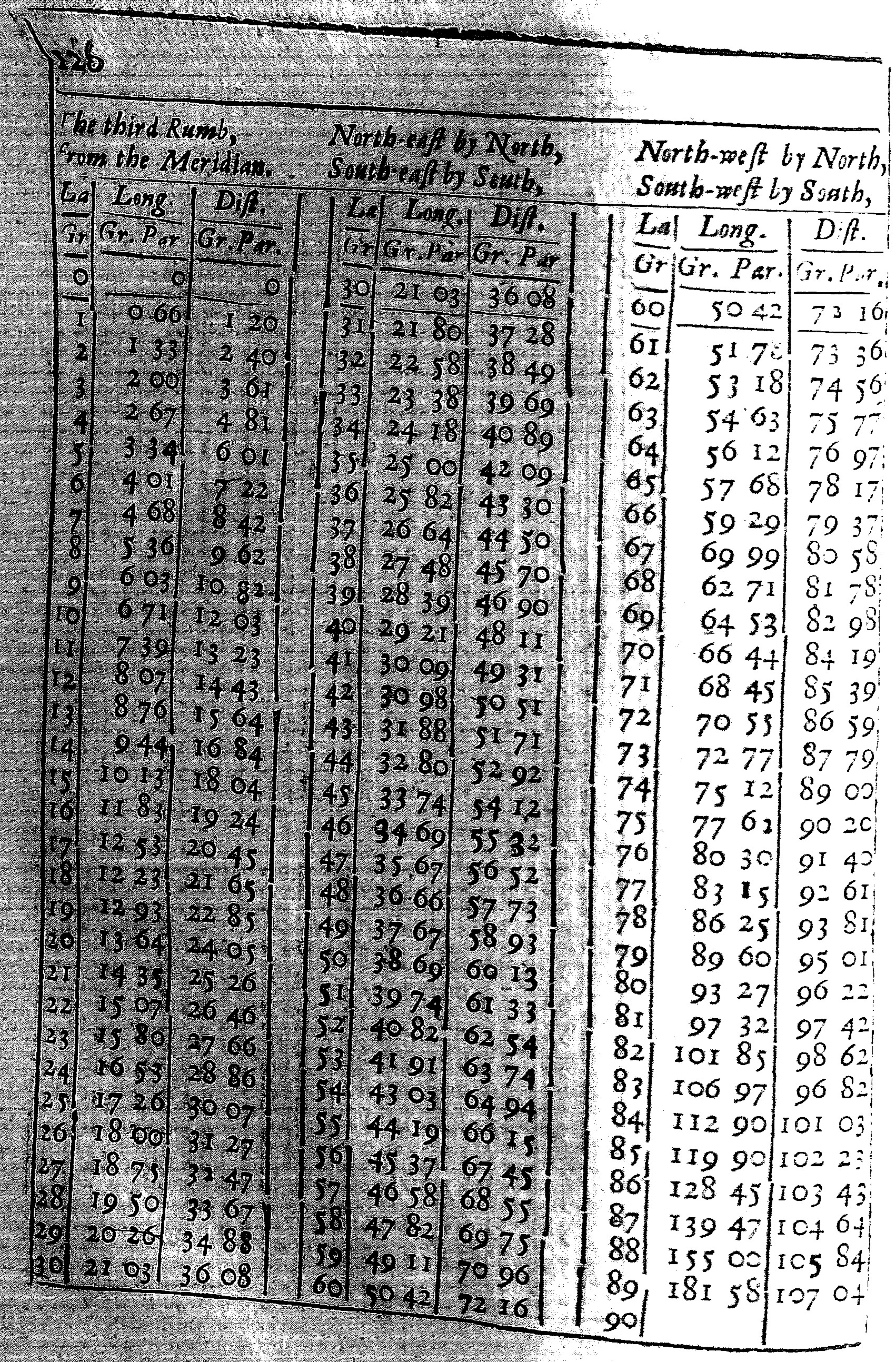
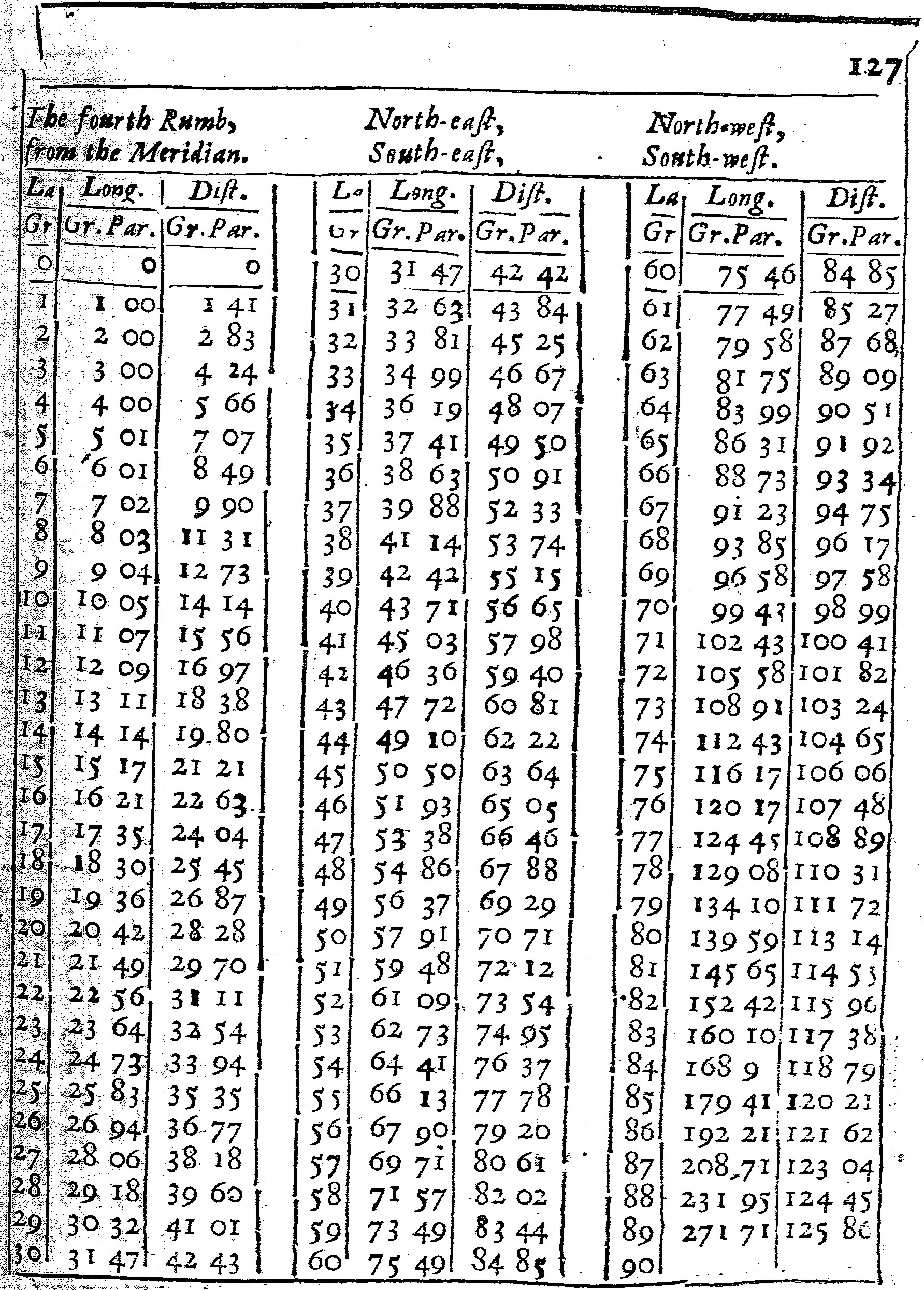
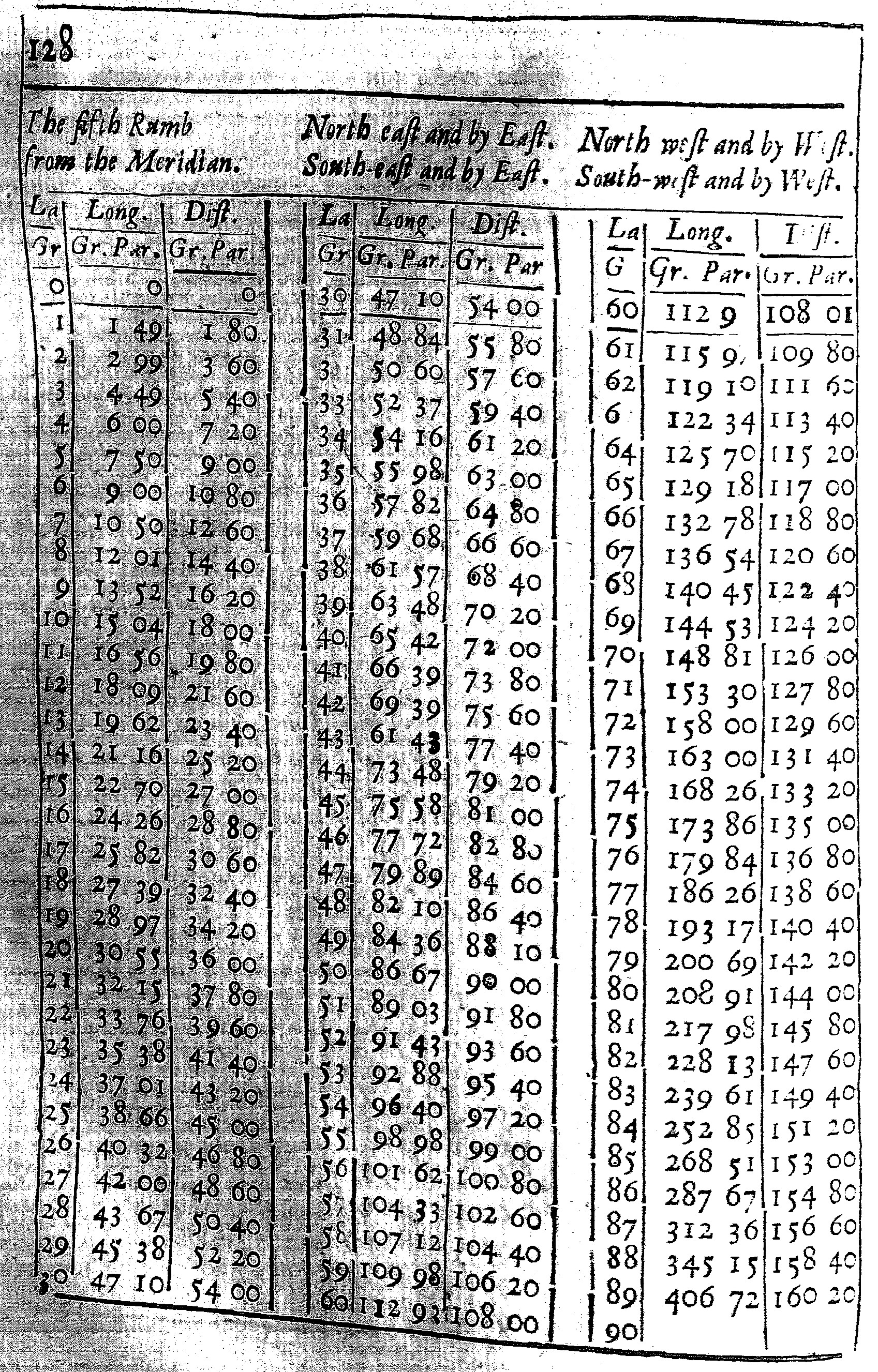
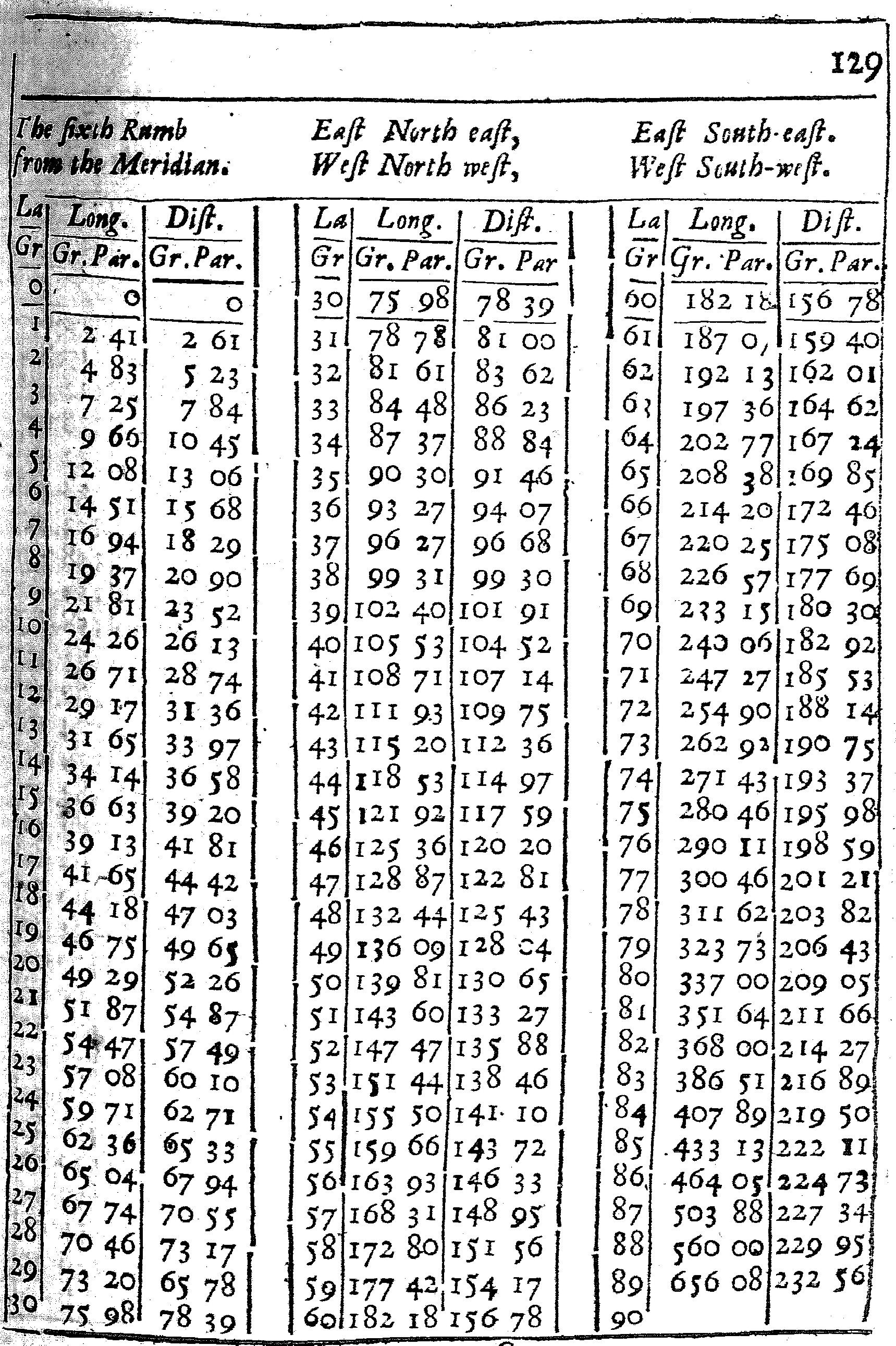
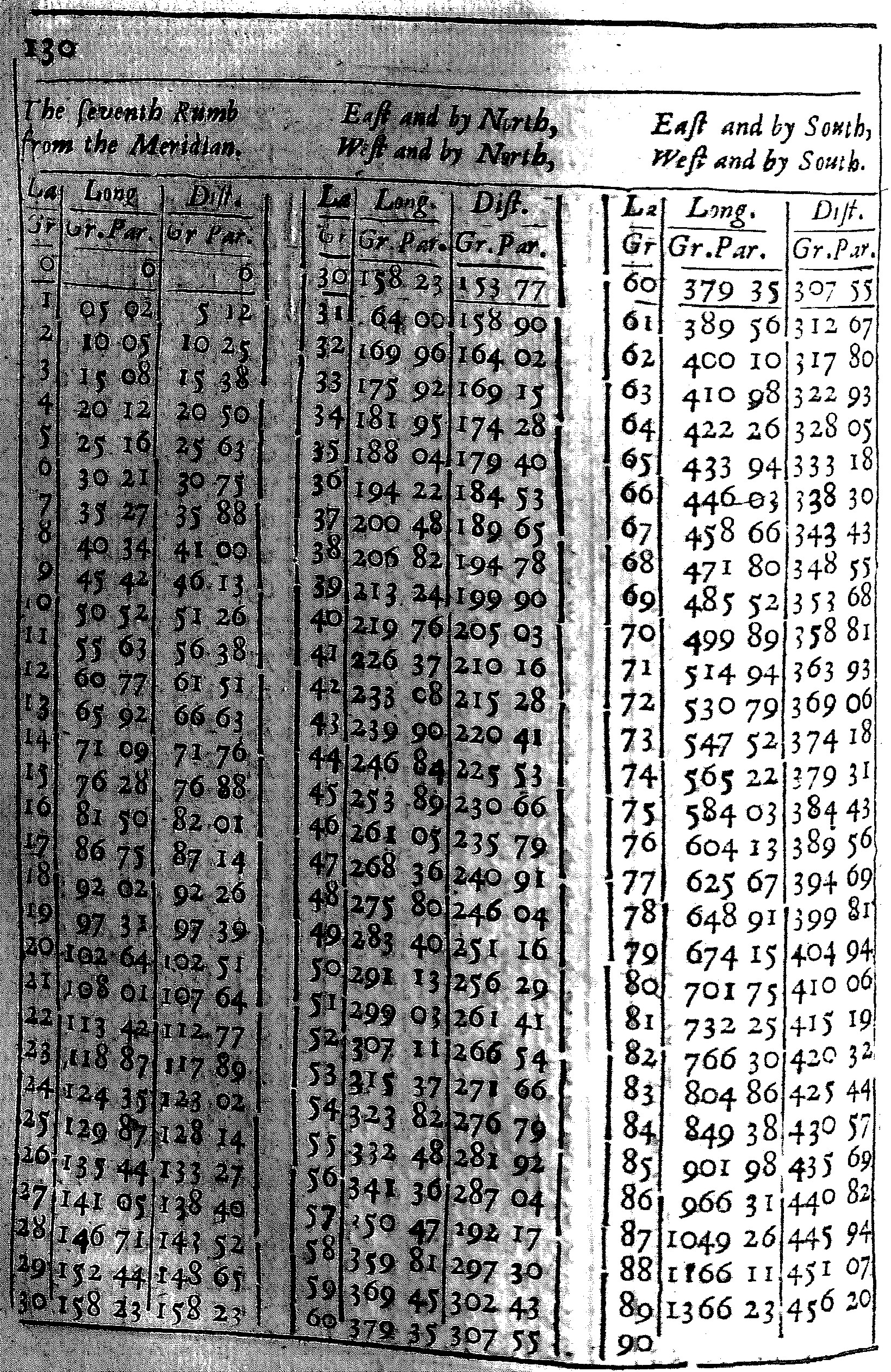
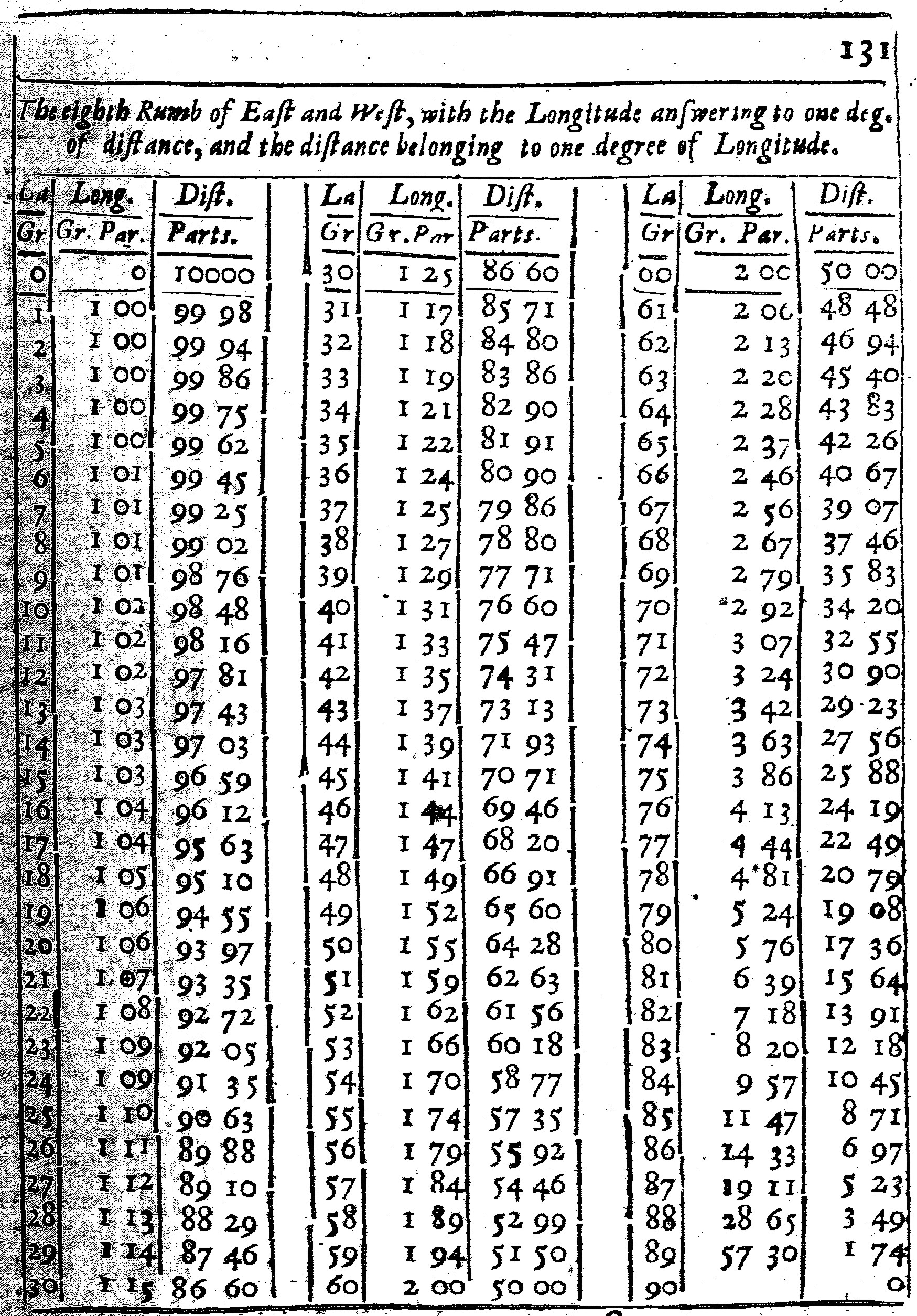
These Tables are calculated for each of the Rumbs.
The first seven have three Colums, and of them the first containeth the degrees of latitude from the Equinoctial to the Pole: the second doth give the difference of Longitude; and the third the distance, both of them belonging to that Rumb and Latitude.
As in the Table of the third Rumb; at the latitude of 50 gr. I find under the title of Longitude 38 gr. 69 parts, and under the title of Distance 60 gr. 13 parts. This shews that if the course held constantly on the third Rumb from the Equinoctial to the Latitude of 50 gr. the difference of Longitude would be 38 gr. 69 parts of 100, and the distance upon the Rumb 60 gr. 13 parts. For here I reckon the distance by degrees, rather than by leagues or Miles, and subdivide each degree into 100 parts, rather than 60 minutes, for the more ease in Calculation, and withal to make the Calculation to agree better, both with his, and my Cross-staff and other Instruments.
The use of these Tables, for the finding of the difference of Longitude is this. Turn the table of the Rumb, and there see what Longitude belongeth to either Latitude, then take the one Longitude out of the other, the Remainder will be the difference of Longitude required.
As in the former Example, where the places given were A, in the Latitude of 50 gr. C in the Latitude of 55 gr. and the Rumb the third from the Meridian: I look into the Table of the third Rumb and there find,
| Latitude 50 gr. | Longitude 38 gr. 69 parts. |
| Latitude 55 gr. | Longitude 44 gr. 10. |
| Therefore the difference of | Longitude 5 gr. 50. |
There is another Use of these tables, for the describing of the Rumb both on the Globe, and all sorts of Charts. For having drawn the Circles of Longitude and latitude, and finding by the tables, the difference of Longitude belonging to each Rumb and latitude: If we make a prick in the Chart, at every degree of Latitude, according to that difference of Longitude, and draw Lines through those Pricks, so as they make no Angles, the Lines so drawn shall be the Rumb required.
The Use of the Eighth Rumb is something different from the rest. For there being here no change of Latitude, I have set to each latitude, the difference of Longitude, belonging to one degree of distance, and the distance belonging to one degree of Longitude.
As if two places shall be 20 Leagues, or one degree distant one from the other, in the Latitude of 50 gr. the difference of Longitude between them will be 1 gr. 55 parts. But if they differ one degree in Longitude, the distance between them will be only 64 parts, which fall short of 13 Leagues, or at the most 64 gr. 28 parts, such as 10000 do make a degree.
6. By the difference of Longitude, Rumb, and one Latitude, to find the other Latitude.
As if the places given were A, in the latitude of 50 gr. C in a greater Latitude, but unknown, the difference of Longitude 5 gr. ½, and the Rumb the third from the Meridian.
In the Chart let AB, DC, the Meridians, be drawn through A and C, according to the difference of Longitude, one 5 gr. ½ from the other; and a Parallel of Latitude through A, crossing the Meridian CD in D: then in A, with AB, make an Angle of the Rumb BAE: so the degrees in the Meridian between D and C, shall be found to be 5 gr. the proper difference of Latitude which was required. Wherefore the proportion holds for the Sector,
- As AD the Radius, to DC the Tangent of the Rumb from the Equator;
- So AD the difference of Longitude, to DC the proper difference of Latitude.
According to this, I take 56 gr. 15 m. for the Angle of the Rumb from the Equator, out of the greater Tangent, and make it a Parallel Radius. Then I reckon 5 gr. ½ in the Line of Lines from the center, for the difference of Longitude. So the parallel taken from the terms of this difference, and measured in the Line of Meridians, shall reach from 50 gr. the latitude given, to 55 gr. which is the latitude required.
Or if the Rumb fall nearer to the Meridian,
- As BC the tangent of the Rumb from the Meridian, is to AB the radius:
- So BC the difference of Longitude, to AD the proper difference of Latitude.
According to this we may best work by parallel entrance; first take 35 gr. 45 m. for the Angle of the Rumb from the Meridian, out of the greater Tangent, and make it a Parallel Radius; then take 5 gr. ½ for the difference of Longitude out of the Line of Lines, and carry it parallel to the former, till the feet of the Compasses stay in like Points: so the Line between the center and the place of this stay, being taken and measured in the Line of Meridians from 50 gr forward, shall shew the latitude required to be 55 gr. as in the former way.
The like may be found by the Table of Rumbs. For in the Table of the third Rumb, at the latitude of 50 gr. I find the Longitude of 38 gr. 69 p. To this I add 5 gr. 50 p. for the difference of Longitude given, the compound Longitude will be 44 gr. 19 p. and this answers to the Latitude of 55 gr.
But if this difference of latitude were to be found by the common Sea-chart, it should seem to be 8 gr. 13 m. and so the second Latitude should be 58 gr. 13 m. which is above 3 gr. more than the truth.
7. By one Latitude, Rumb, and distance, to find the difference of Longitude.
As if the places given were A in the Latitude of 50 gr, c in a greater latitude but unknown, the distance upon the Rumb be 5 gr. between them, and the Rumb the third from the Meridian.
In the Chart, let a Meridian AB, and a Parallel AD, be drawn through A, and in A, with AB, make an Angle BAC, for the Rumb from the Meridian; then open the Compasses according to the Latitude of the places to EF, the quantity of 6 gr. in the Meridian, transferring them into the Rumb from A to C, and through C draw another Meridian DC, crossing the Parallel drawn through A in D, so the degrees intercepted in the Parallel from A to D, shall shew the difference of the Longitude required to be about 5 gr ½. Wherefore the proportion holds for the Sector.
- As AC, the Radius, is to AD, equal to BC, the Sine of the Rumb fom the Meridian:
- So AC the proper distance upon the Rumb, to AD the difference of Longitude.
According to this I take the Sine of 33 gr. 45 m. for the Angle of the Rumb from the Meridian, and make it a Parallel Radius; then keeping the Sector at this Angle, I take 6 gr. for the distance, out of the Meridian Line, according to the estimated Latitude of both places, and lay it on both sides of the sector from the center: so the parallel taken from both terms of this distance, and measured in the Line of Lines, shall shew the difference of Longitude to be about 5 gr. ½.
In this and some of the Prop. following, where there is but one Latitude known, there may be sometimes an error of a minute or two, in the estimation of the proper distance, yet it may be rectified at a second operation.
This Proposition may also be wrought by the Tables of Rumbs. For according to the Example, in the table of the third Rumb, at the latitude of 50 gr. I find the Longitude of 38 gr. 69 p. and the distance of 60 gr. 13 p. to this I add 6 gr. for the distance given; so the compound distance will be 66 gr. 13 p. and this answers to the Longitude of 44 gr. 19 p. then if I take the one Longitude out of the other, the difference will be 5 gr. 50 p. as before.
But if this difference were to be found by the common Sea-chat, it should seem to be only 3 gr. 20 m. which is more than 2 gr. less than the truth.
8. By one Latitude, Rumb, and difference of Longitudes, to find the distance.
As if the places given were A, in the latitude of 50 gr. C in a greater Latitude but unknown, the difference of Longitude between them being 5 gr. ½, and the Rumb the third from the Meridian.
In the Chart let AB, DC, Meridians be drawn through A nad C, according to the difference of Longitude, and a Parallel of Latitude through A, crossing the Meridian DC in D; then in A, with AB, make an Angle of the Rumb BAC: so the distance on the Rumb from A to C taken and measured in the Meridian, according to the estimated Latitude of the places, shall be found to be 6 gr. Wherefore the proportion holds for the Sector.
- As AD, equal to BC, the Sine of the Rumb from the Meridian, is to AC the Radius:
- So AD the difference of Longitudes, to AC the proper distance upon the Rumb.
According to this, I take the lateral Radius, and make it a Parallel Sine of 33 gr. 45 m. which is here the Angle of the Rumb from the Meridian; then I reckon 5 gr. ½ in the Line of Lines from the Center, for the difference of Longitude: so the Parallel taken from the terms of this difference, and measured in the Line of Meridians, according to the Latitudes of the places, shall there shew the distance required to be about 6 gr. which are 120 Leagues.
Or if the Rumb shall fall nearer to the Meridian, that the lateral Radius cannot be fitted over in his Sine, this Prop. must be wrought by Parallel entrance, and so also it gives the same distance as before.
Or we may find this distance by the Table of Rumbs. For in the Table of the third Rumb, at the latitude of 50 gr. I find the Longitude of 38 gr. 69 p. and the distance of 60 gr. 13 p. To this Longitude here found, I add 5 gr. 50 p. for the difference of Longitude given: so the compound Longitude will be 44 gr. 19 p. and this answers to the distance of 66 gr. 15 p. Then if I take the one distance out of the other, the remainder will be 6 gr. 2 p. for the distance required.
But if this distance were to be measured on the common Sea-chart, it should seem to be almost 10 gr. or as the least 197 Leagues, above 77 Leagues more than the truth.
9. By one Latitude, distance, and difference of Longitude, to find the Rumb.
As if the places given were A, in the latitude of 50 gr. C in a greater Latitude but unknown, the difference of Longitude between them being 5 gr. ½,, and the distance 6 gr. upon the Rumb.
In the Chart AB, DC, Meridians, be drawn through A and C, and a Parralel of Latitude through A; then open the Compasses according to the Latitudes of the places, to EF the quantity of 6 gr. in the Meridian, and setting the one foot in A, the other foot shall cross the other Meridian in C: and if we draw the right Line AC, the Angle BAC shall shew the inclination of the Rumb to the Meridian, to be about 33 gr. 45 m. Wherefore the proportion holds for the Sector,
- As AC the proper distance upon the Rumb, is to AD the difference of Longitude:
- So AC Radius, to AD, equal to BC, the Sine of the Rumb from the Meridian.
According to this, I take the proper distance 6 gr. out of the Line of Meridians, and lay it on both sides of the Sector from the Center; then I take the difference of Longitude 5 gr. ½ out of the Line of Lines, and to it open the Sector in the terms of the former distance: so the Parallel Radius taken from between 90 and 90, and measured in the Sines, doth give about 33 gr. 45 m. for the Rumb required.
But if this Rumb were found by the common Sea-chart, it should seem to be above 66 gr. and so almost the sixth Rumb from the Meridian.
10. By the Longitude and latitude of two places, to find their distance upon the Rumb.
Let the Sector be opened in the Line of Lines unto a right Angle (as was shewed before Chap. 2. Pro. 7.) then take out the proper difference of Latitude, and lay it on the Line, and the difference of Longitude, and lay it on the other line, so as they may both meet in the Center, marking how far they extend. For the Line taken from the terms of their extension, and measured in the Meridian, according to their Latitude, shall shew the distance required.
So if the places given were A and C, A in the Latitude of 50 gr. C in the latitude of 55 gr. the proper difference of Latitude shall be the Line AB, and let BC the difference of Longitude be 5 gr. ½. We shall find that AC the distance upon the Rumb is about 6 gr. which make 120 Leagues.
For in the Chart, let an occult Meridian be drawn through A, and a Parallel of Latitude through C, crossing the former Meridian in B, and a right Line for the Rumb, from A to C, so have we a Rectangle Triangle ABC, whose Base AC, taken and measured in the Meridian from E below 50 gr. to F, as much above 55 gr. doth contain the quantity of 6 gr.
In the same manner the Sector being opened to a right Angle, in the Line of Lines; if we take the difference of Latitude out of the Line of Meridians, in his proper place from 50 gr. to 55 gr. and place it on one of the sides from the center, to resemble AB, then reckon the difference of Longitude on the other Perpendicular Line from the Center to 5 gr. ½, instead of BC, we shall have the like Rectangle Triangle on the Sector, to that which we had before on the Chart; and if we take out the Base of it, and measure it in the Line of Meridians from below 50 gr. to as much above 55 gr. we shall find as before, that it containeth 6 gr. or 120 Leagues.
But if this distance were to be measured on the common Sea-chart, it should seem to be almost 7 gr. ½ or 145 Leagues; which is 25 leagues more than truth.
11. By the Latitude of two places, and the distance upon the Rumb, to find the difference of Longitude.
Let the Sector be opened in the Lines of Lines to a right Angle, then take out the proper difference of Latitude, and lay it on one of the Lines from the Center, then take the proper distance with a pair of Compasses, and setting one foot in the terms of the difference, turn the other foot to the other Line of the Sector, and it shall there shew the difference of Longitude required.
So if the place given were A in the Latitude of 50 gr. C in the Latitude of 55 gr. with 6 gr of distance one from the other, we shall find their difference of Longitude to be about 5 gr. ½.
For in the Chart let a Meridian AB be drawn for the one, and AC, AD, Parallels of Latitude for them both: Then open the Compasses according to the Latitude of the places, to EF the quantity of 6 gr. in the Meridians, and setting one foot in A, having Latitude of 50 gr. turn the other to the Parallel of 55 gr. and it shall there cut off the required difference of Longitude BC 5 gr. ½.
In the same manner, the Sector being opened to a right Angle, in the Lines of Lines: if we take the difference of Longitude out of the Line of Meridians in his proper place from 50 gr. unto 55 gr. and place it on one of the Lines from the Center; then take 6 gr. the distance upon the Rumb out of the same Line of Meridians, according to the Latitudes of the places, and set one foot in the term of the former difference, turning the other foot to the other Perpendicular Line, we shall find it will cross it about 5 gr. ½ from the Center, which is the difference of Longitude required.
But if this difference of Longitude were to be found by the common Sea-chart, it would seem to be only 3 gr. 20 m. which is more than 2 gr. 10 m. less than the truth.
12. By one Latitude, distance and difference of Longitudes, to find the difference of Latitudes.
Let the Sector be opened in the Lines of Lines to a right Angle, and let the difference of Longitude be reckoned in one of those Lines from the Center; then take the proper distance with a pair of Compasses, and setting the one foot in the term of the former difference, turn the other foot to the other Line of the Sector, and it shall thence cut off a Line, equal to the proper difference of latitude required.
So if the places given were A and C, A in the Latitude of 50 gr. C in a greater Latitude but unknown, the difference of Longitude between them 5 gr. ½, and the distance upon the Rumb 6 gr. or 120 Leagues, we shall find the difference of Latitude to be 5 gr.
For in the Chart, let occult Meridians be drawn through A and C, and a Parallel of Latitude through A, the open the Compasses according to the estimated Latitudes of the places to EF the quantity of 6 gr. in the Meridian, and setting the one foot in A, turn the other to the Meridian drawn through, and it shall there cut off the Line DC, which is the difference of Latitude required.
In the same manner, the Sector being opened to a right Angle in the Line of Lines, if in the one Line we reckon the difference of Longitude from the Center to 5 gr. ½, then taking 6 gr. for the difference out of the Line of Meridians, according to the Latitude of the places, we set the other foot in the term of the given difference, and turn the other foot to the other Perpendicular Line, we shall find that it cuts a Line from it, which taken and measured in the Kline of Meridians, from 50 gr. on forward, doth shew the difference of Latitude to be as before.
But if this difference of Latitude were to be found by the common Sea-chart, it would seem to be only 2 gr. 25 m. which is 2 gr. 35 m. less than the Truth. Such is the difference between both these Charts.