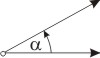
spitzer Winkel, α < 90°
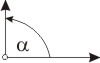
rechter Winkel, α = 90°
stumpfer Winkel, α > 90°
gestreckter Winkel, α = 180°
überstumpfer Winkel, α gt; 180°
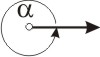
Vollwinkel, α = 360°
Das typische Lehrbuch der Geometrie beginnt mit der Erklärung der Begriffe Punkt, Gerade, Strahl und Strecke, und der Definition ihrer Eigenschaften. Das schenke ich mir hier. Das folgende Kapitel des Lehrbuchs beschäftigt sich dann mit dem Winkel.
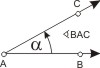
Zwei von einem Punkt ausgehende Strahlen bilden einen Winkel. Die beiden Strahlen werden Schenkel genannt, der gemeinsame Punkt A der beiden Strahlen heißt Scheitel des Winkels. Winkel werden mit kleinen griechischen Buchstaben symbolisiert, oder man bezeichnet einen Winkel mit drei Buchstaben ∠BAC, wobei der mittlere Buchstabe den Scheitel des Winkels angibt. Winkel werden in (Bogen-)Grad (Symbol: °) gemessen, wobei der Vollkreis in 360° geteilt ist.
Nach der Anzahl Grad, die der Winkel einschließt, unterscheidet man:
 spitzer Winkel, α < 90° |
 rechter Winkel, α = 90° |
stumpfer Winkel, α > 90° |
|
gestreckter Winkel, α = 180° |
überstumpfer Winkel, α gt; 180° |
 Vollwinkel, α = 360° |
Zwei Winkel, die den Scheitel und einen Schenkel gemeinsam haben und deren Summe 180° beträgt, heißen Supplementwinkel (Ergänzungswinkel). Es gilt: α + β = 180°
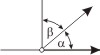
Zwei Winkel, die den Scheitel und einen Schenkel gemeinsam haben und deren Summe 90° beträgt, heißen Nebenwinkel oder komplementäre Winkel. Es gilt: α + β = 90°
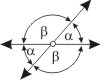
Durch die Verlängerung beider Schenkel eines Winkels über den Scheitel hinaus entstehen vier Winkel. Die beiden Verlängerungen schließen den Scheitelwinkel von α ein. Gegenüberliegende Scheitelwinkel sind gleich. Es gilt: α + β = 180°
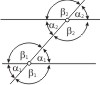
Zwei Geraden in einer Ebene, die sich nicht schneiden, heißen Parallelen. Werden zwei Parallelen von einer dritten Geraden geschnitten, so sind:
Dieses Gesetz nutzte Eratosthenes (um 273-um 194 v. Chr.) um den Erddurchmesser zu bestimmen.
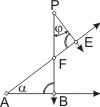
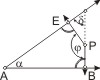
Stehen die Schenkel zweier Winkel paarweise senkrecht aufeinander, so:
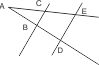
Schneiden zwei Parallelen die Schenkel eines Winkels, so gilt nach Thales von Milet für die Abschnitte auf den Schenkeln und den Parallelen:
Seit der Renaissance wird dieser Strahlensatz als Proportionalzirkel zum Berechnen von 3-Satz Aufgaben verwendet. Eine wichtige Anwendung ist der Sector von Edmund Gunter, auf dem logarithmische Skalen eingezeichnet waren.
© Dr. Rainer Stumpe, URL: https://www.rainerstumpe.de