Die Winkelskalen

Die Logarithmen und der Rechenschieber wurden anfänglich ausschließlich von Kaufleuten und See­fah­rern benutzt. Beide haben erheblichen Rechenbedarf: Kaufleute z. B. die Zinsberechnungen, Seeleute Navi­gationsaufgaben. Für die Navigation gibt es auf dieser Site ausführliche Beispiele — einschließlich der tri­go­no­me­tri­schen Grundlagen. In jüngerer Zeit haben besonders Piloten den Rechenschieber für die Be­rech­nung von Kurskorrekturen bei Abdrift durch Seitenwind benutzt. Von Aristo gab es deshalb spe­ziel­le Rechen­scheiben (Naviat, Aviat) für die Navigation, und in England den Unique Navigator.

Ein hübsches Beispiel zum Rechnen mit trigonometrischen Skalen wird im Kapitel Sphä­ri­sche Tri­go­no­metrie bei der Berechnung der Tageslänge ausgeführt.

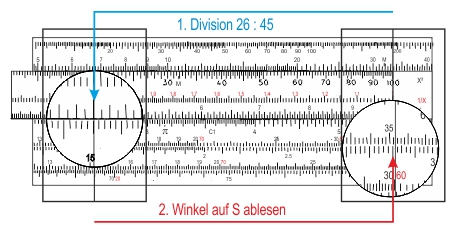
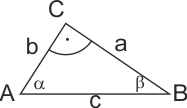Den üblichen Rechenschieber setzt man aber ein, um Zah­len­wer­te der Winkelfunktionen abzulesen, oder um aus einer Rech­nung den zugehörigen Winkel zu bestimmen. Ein Beispiel ist der Winkel in einem recht­wink­ligen Dreieck mit bekannten Sei­ten­län­gen (siehe zur Definition der Winkelfunktionen). Den Win­kel α zwischen der Ankathete b und der Hypotenuse c mit den Längen 26 cm und 45 cm erhält man aus der Be­zie­hung:

• cos α = Ankathete b : Hypotenuse c = 26 : 45 ⇒ α = 54,7°.

Achtung: Der Cosinus wird auf der Skala S von Rechts nach links abgelesen. Sinus und Cosinus sind ja zyklische Funktionen die Funktionswerte zwischen 0 und 1 annehmen, und die um 90° verschoben sind — genau die Länge der Winkelwerte-Skala auf dem Rechenschieber.

Die Länge der Gegenkathete kann man auf drei Wegen berechnen:

1. nach dem Satz des Pythagoras (a² + b² = c²)
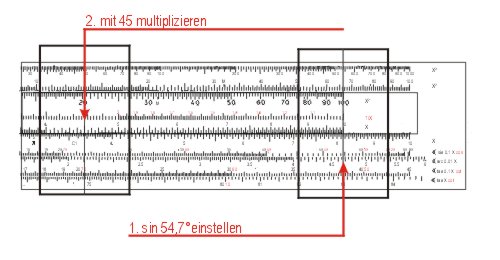
2. sin α = Gegenkathete a : Hypotenuse c ⇒ Gegenkathete =  Hypotenuse c · (sin α ),
3. mit der pythagoreischen Skala, wenn man einen Rechenschieber des Systems Darmstadt hat.

1. Nach dem Pythagoras (a ist die Gegenkathete, c die Hypotenuse) ist die Länge von a:

   • .

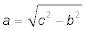   Die Werte c und b werden nacheinander auf der Skala C eingestellt und auf der Skala B werden die Quadrate abgelesen (hier hilft es die letzte Ziffer zu schätzen, wenn man weiß, dass die Quadrate gerader Zahlen auch gerade sind, und dass die Quadrate von durch 5 teilbaren Zahlen auch eine 5 als letzte Ziffer haben).
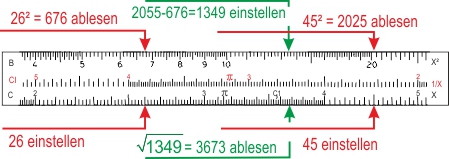
   Die Differenz wird manuell gebildet (1349), aber wo soll man sie nun auf B einstellen, bei 1,349 oder bei 13,49? Als Regel gilt: alle ungerad-stelligen (1,3,5...-stellig) Quadratzahlen werden auf der linken, alle gerad-stelligen (2, 4, 6, …-stellig) auf der rechten Hälfte der Skala eingestellt. Auf C liest man dann die Wurzel ab: a = 36,8.

2. Mit Winkelfunktionen müssen wir den Sinus von α = 54,7° mit der Hypotenusenlänge c = 45 multiplizieren. Das Ergebnis 36,7 liest man auf D ab.
   • 
3. Die Berechnung mit der pythagoreischen Skala ist bei der Erläuterung der Skalen des Rechenschiebers ausgeführt.