Entfernungs- und Abstandsbestimmungen
Der Navigator kennt folgende Entfernungsbestimmungen:
- mit Höhenwinkelmessung:
- mit Horizontalwinkelmessung:
Versegelungspeilung
Bei der Versegelungspeilung fährt man mit konstanter Geschwindigkeit und konstantem Kurs eine zeitlang an einem Objekt mit bekannter Position, z. B. einer Tonne oder einer Landmarke, vorbei. Da man keine 2. Peilung hat kann man nicht unmittelbar einen Schiffsort bestimmen. Mit Hilfe des Sinussatzes lässt sich aber der Abstand zur Tonne, an der man vorbei gesegelt ist, berechnen.
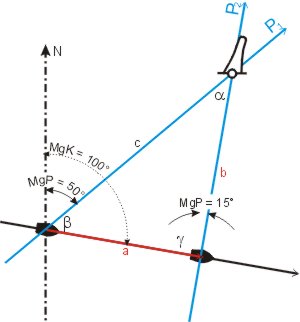 Das Boot fuhr mit rwK 100° und einer Geschwindigkeit von 6,5 kn zwischen der ersten Peilung (rwP1 = 50°) bis zur 2. (rwP2 = 15°) 1 ¼ Stunde (75 min). Die Strecke a ist damit 8,125 sm lang (zur Erinnerung: das geht toll mit dem Rechenschieber zu lösen!).
Die beiden anderen Dreiecksseiten b und c stehen zu der bekannten Entfernung a nach dem Sinussatz
mit den Winkeln im Verhältnis.
Das Boot fuhr mit rwK 100° und einer Geschwindigkeit von 6,5 kn zwischen der ersten Peilung (rwP1 = 50°) bis zur 2. (rwP2 = 15°) 1 ¼ Stunde (75 min). Die Strecke a ist damit 8,125 sm lang (zur Erinnerung: das geht toll mit dem Rechenschieber zu lösen!).
Die beiden anderen Dreiecksseiten b und c stehen zu der bekannten Entfernung a nach dem Sinussatz
mit den Winkeln im Verhältnis.
Für die Entfernung zum Feuer bei der ersten Peilung gilt:
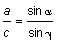 ,
,
für die bei der 2. Peilung entsprechend
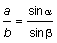 .
.
Jetzt folgt ein wenig Winkelarithmetik um die Winkel β und γ aus dem Kurs und den Peilungen zu berechnen.
- β = Kurs - Peilung 1 = 100° - 50° = 50°;
- für γ kann der Außenwinkel zu 100° - 15° direkt erkannt werden, damit ergibt sich
- γ = 180° - 85° = 95°;
(geht auf dem Rechenschieber nicht einzustellen! Aber es gilt sin (180° - α) = - sin α, wir können also mit sin (180° - 95°) = sin 85° rechnen).
Der Winkel α ergänzt die Summe der beiden anderen zu 180° (Winkelsumme im Dreieck):
- α = 180° - 50° - 95° = 35°.
Hinweis: Wenn man eine Seiten- bzw. Bordpeilung macht, also den Winkel zur Bootsachse misst, kann man sich die aufwändige Winkelberechnung sparen: man liest die Winkel β und γ direkt ab.
Beispielrechnung
Aus der Gleichung
erhält man den Ausdruck für die Länge von c:
- c = a · sin γ ⁄ sin α = 8 sm · sin 85° ⁄ sin 35° = 13,9 sm
sin 35° ablesen und notieren (wird noch einmal gebraucht). Läufer auf 35° Skala S, auf Skala D ablesen: 0,574. Läufer auf 85° auf Skala S, 10 auf Skala C unter den Läufer, Läufer auf 8 (Skala C), 0,574 (Skala C) unter Läufer, bei 1 (Skala D) auf Skala C ablesen: 13,9 sm.
Aus der Gleichung
erhält man den Ausdruck für b:
- b = a · sin β ⁄ sin α = 8 sm · sin 50° ⁄ sin 35° = 10,65 sm
Läufer auf 50° auf Skala S, 10 auf Skala C unter den Läufer, Läufer auf 8 (Skala C), 0,574 (Skala C) unter Läufer, bei 1 (Skala D) auf Skala C ablesen: 10,65 sm.
Die Entfernung zum Feuer betrug bei der 1. Peilung 13,9 sm, bei der zweiten 10,65 sm. Nun kann man zwei beobachtete Orte in die Karte eintragen: es sind dies die Schnittpunkte der Peilung zur Tonne mit den beiden Abstandskreisen. Die Unsicherheit ist in der Geschwindigkeitsmessung begründet.
Verfahren mit dem Rechenschieber
Nach diesem Schema würde man mit dem Taschenrechner rechnen. Der mit dem Rechenschieber geübte Navigator erinnert sich an die andere Form des Sinusatzes:
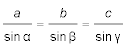 ,
,
oder in Worten:
"Die Seiten eines schiefwinkligen Dreiecks verhalten sich wie die Sinuswerte der den Seiten gegenüberliegenden Winkel."
Bei solchen Proportionalitäten spielt der Rechenschieber seine Vorteile aus: mit einer Einstellung der Zunge und Verschieben des Läufers erhält man alle gewünschten Werte.
Hat man die beiden Deckspeilungen β = 50° (1. Peilung) und γ = 95° (2. Peilung) (und daraus den dritten Winkel α = 35°, der der Seite a gegenüberliegt), und die Entfernung a = 8 sm, so stellt man den Läuferstrich über α = 35° auf der Sinusskala S und die versegelte Strecke a auf der Zungenskala C unter den Läuferstrich (in unserem Beispiel müssen wir noch die Zunge "durchschiebe", d. h. wir verschieben den Läufer auf die "1" der Skala C und verschieben die Zunge damit die "10" am anderen Ende der Skala unter dem Strich steht). Jetzt braucht man nur noch den Läufer nach einander auf die Winkel β und γ zu verschieben, und kann auf der Skala C direkt die Entfernung zum Objekt bei der ersten und der zweiten Peilung ablesen: zur ersten Peilung β = 50° gehört die 2. Entfernung b = 10,68 sm, zur zweiten Peilung sin γ = sin 95° = sin 85° gehört die erste Entfernung c = 13,85 sm.
Die Geschwindigkeit, mit der diese Rechnung möglich ist, sollte ein Taschenrechner einmal nachmachen!
Vierstrichpeilung, Verdoppelungspeilung
Eine Variante der Versegelungspeilung ist die Vierstrichpeilung. Bei ihrer Anwendung nutzt man die Eigenschaften des gleichschenkligen Dreiecks aus. Sie hat den Vorteil, dass man das Ergebnis im Kopf ausrechnen kann, und den Nachteil, dass man längere Zeit peilen muss, um den richtigen Zeitpunkt zu erwischen.
In diesem Abschnitt wird unter "Peilung" immer die Deckspeilung verstanden, d. h. der Peilwinkel bezogen auf die Bootslängsachse!
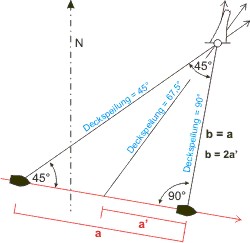 Im gleichschenkligen Dreieck gilt: zwei Seiten sind gleichlang, und die diesen anliegenden Winkel sind gleich. Ist das Dreieck zudem rechtwinklig, betragen die beiden der dritten Seite anliegenden Winkel 45° (weil die Winkelsumme im Dreieck 180° beträgt). Peilt man nun ein Objekt unter 45°, und segelt bis man es querab (unter 90°) sieht, dann entspricht die versegelte Strecke der Entfernung zum Objekt am Ort der 90°-Peilung. (Durch die beiden Peilwinkel wird ein gleichschenkliges Dreieck definiert!) Der Name Vierstrichpeilung stammt aus der Zeit der großen Segler. Damals war der Kompass nicht in 360 Grad, sondern in 32 Striche eingeteilt. Jeder Strich entspricht 11,25°, und 45° sind entsprechend 4 Striche. Man segelt also unter konstantem Kurs mit konstanter Geschwindigkeit und stoppt die Zeit, die man zwischen der 45°-Peilung und der 90°-Peilung benötigt, rechnet mit dem
Rechenschieber die Fahrtstrecke aus, und hat zur Peilung noch die Entfernung, also zwei Standlinien deren Schnittpunkt den Schiffsort definieren.
Im gleichschenkligen Dreieck gilt: zwei Seiten sind gleichlang, und die diesen anliegenden Winkel sind gleich. Ist das Dreieck zudem rechtwinklig, betragen die beiden der dritten Seite anliegenden Winkel 45° (weil die Winkelsumme im Dreieck 180° beträgt). Peilt man nun ein Objekt unter 45°, und segelt bis man es querab (unter 90°) sieht, dann entspricht die versegelte Strecke der Entfernung zum Objekt am Ort der 90°-Peilung. (Durch die beiden Peilwinkel wird ein gleichschenkliges Dreieck definiert!) Der Name Vierstrichpeilung stammt aus der Zeit der großen Segler. Damals war der Kompass nicht in 360 Grad, sondern in 32 Striche eingeteilt. Jeder Strich entspricht 11,25°, und 45° sind entsprechend 4 Striche. Man segelt also unter konstantem Kurs mit konstanter Geschwindigkeit und stoppt die Zeit, die man zwischen der 45°-Peilung und der 90°-Peilung benötigt, rechnet mit dem
Rechenschieber die Fahrtstrecke aus, und hat zur Peilung noch die Entfernung, also zwei Standlinien deren Schnittpunkt den Schiffsort definieren.
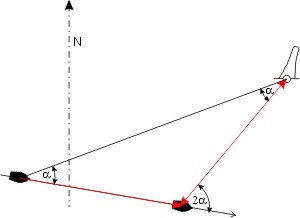 Die Eigenschaft des gleichschenkligen Dreiecks kann man zur "Peilungsverdopplung" ausnutzen: immer, wenn der zweite Peilwinkel genau doppelt so groß ist wie der der ersten Peilung, ist die Entfernung zum Peilobjekt zur Zeit der zweiten Peilung genau gleich der seit der ersten versegelten Strecke. Denn der Innenwinkel im Dreieck, der zu dem Außenwinkel 2 · α gehört beträgt 180° - 2 · α, der dritte Winkel am Objekt ist also
Die Eigenschaft des gleichschenkligen Dreiecks kann man zur "Peilungsverdopplung" ausnutzen: immer, wenn der zweite Peilwinkel genau doppelt so groß ist wie der der ersten Peilung, ist die Entfernung zum Peilobjekt zur Zeit der zweiten Peilung genau gleich der seit der ersten versegelten Strecke. Denn der Innenwinkel im Dreieck, der zu dem Außenwinkel 2 · α gehört beträgt 180° - 2 · α, der dritte Winkel am Objekt ist also
- 180° - 2 · α - (180° - 2 · α) -2 α = α
⇒ das Dreieck muß gleichschenklig sein, denn zwei Winkel sind gleich. Das Problem der Abstandsmessung reduziert sich auf eine Zeitmessung (wenn die Geschwindigkeit konstant war)! Den Rechenschieber braucht man nur noch, um die Fahrstrecke aus der Fahrtzeit und der Geschwindigkeit zu berechnen.
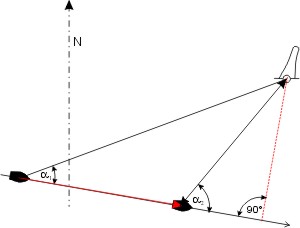 Gelegentlich kann es interessant sein, durch Peilung festzustellen, in welcher Entfernung man ein Hinderniss, z. B. ein Kap, querab passieren wird, ohne in der Karte Standorte und Kurse einzuzeichnen. Dazu gibt es Tabellen von Peilungs-Winkelpaaren, bei denen die Dwarsentfernung im Zusammenhang mit der versegelten Strecke steht.
Gelegentlich kann es interessant sein, durch Peilung festzustellen, in welcher Entfernung man ein Hinderniss, z. B. ein Kap, querab passieren wird, ohne in der Karte Standorte und Kurse einzuzeichnen. Dazu gibt es Tabellen von Peilungs-Winkelpaaren, bei denen die Dwarsentfernung im Zusammenhang mit der versegelten Strecke steht.
Man unterscheidet Winkelpaare, für die die versegelte Strecke gleich it der Querab-Entfernung, und solche, für die die Dwarsentfernung ein Bruchteil der Versegelung ist. Hier unten stehen Beispeile. Mit der trigonometrischen Ableitung kann man leicht zusätzliche Winkelpaare finden.
| Erste Peilung | Zweite Peilung |
|
|
|
| 22° | 34° |
| 25° | 41° |
| 27° | 46° |
| 29° | 51° |
| 32° | 59° |
| 40° | 79° |
| 44° | 88° |
| 45° | 90° |
|
|
|
| Erste Peilung | Zweite Peilung | querab Entfernung |
| 22,5° | 45° | 7 ⁄ 10 der Versegelung |
| 30° | 60° | 7 ⁄ 8 der Versegelung |
Trigonometrischen Erklärung
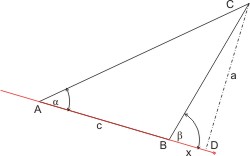 Das Schiff segelt auf der roten Linie. Am Ort A wird das Objekt C unter dem Winkel α, und nach einer Fahrt von A nach B (AB = c) am Ort B unter dem Winkel β gepeilt. Gefragt ist die querab Entfernung a vom Objekt C. (Die Strecke CD = a ist das Lot auf den Kurs des Schiffs.) Wir erkennen zwei rechtwinklige Dreiecke: ADC und BDC, und können mit der Definition der Winkelfunktionen die beiden Gleichungen formulieren:
Das Schiff segelt auf der roten Linie. Am Ort A wird das Objekt C unter dem Winkel α, und nach einer Fahrt von A nach B (AB = c) am Ort B unter dem Winkel β gepeilt. Gefragt ist die querab Entfernung a vom Objekt C. (Die Strecke CD = a ist das Lot auf den Kurs des Schiffs.) Wir erkennen zwei rechtwinklige Dreiecke: ADC und BDC, und können mit der Definition der Winkelfunktionen die beiden Gleichungen formulieren:
Aus der zweiten Formel erhält man: x = a ⁄ tan β und kann x in der ersten Formel substituieren:
- a = (c + x) · tan α = (c + a ⁄ tan β) · tan α
Da uns nur der Fall interessiert wo die versegelte Strecke a gleich der Dwarsentfernung a ist, können wir die Gleichung in der Form betrachten:
- a = a · tan α + a · tan α ⁄ tan β
- 1 = tan α · (1 + 1 ⁄ tan β)
Da diese Gleichung umständlich zu berechnen ist, formt man um:
Diese Gleichung ist transzendent, d. h. man kann sie nicht lösen — wie die Kepler-Gleichung. Man muss iterativ die Paare von α und β suchen, für die tan α · tan β ⁄ (tan β - tan α) = 1 ist, wenn die Versegelung c gleich dem Dwarsabstand a sein soll.
Man kann die Wertepaare der obigen Tabellen leicht mit MS® Excel® nachprüfen (und natürlich weitere Paare finden):
| α | β | Faktor a ⁄ c |
| 22° | 34° | 1,0 |
| 25° | 41° | 1,0 |
| 27° | 46° | 1,0 |
| 29° | 51° | 1,0 |
| 32° | 59° | 1,0 |
| 40° | 79° | 1,0 |
| 44° | 88° | 1,0 |
| 45° | 90° | 1,0 |
| 22,5° | 45° | 0,7 = 7 ⁄ 10 |
| 30° | 60° | 0,9 = 7 ⁄ 8 |