Berechnung der Zahlenwerte der Winkelfunktionen
Wenn man die Zahlenwerte des Sinus oder Cosinus eines Winkels haben möchte, so muss man wohl ein Bild malen und die Länge der halben Sehne des Einheitskreises ausmessen. Das Ergebnis kann man dann mit dem Satz des Pythagoras überprüfen: 12 = sin2α + cos2α. Das ist natürlich nicht sehr genau, denn man kann mit einem Lineal ja höchstens etwa 0,1 mm abschätzen.
Man verwendet also einen Kreis mit 1 m Radius und erhält für 1° ⁄ 10 eine Halbsehen der Länge 1,7 mm. Der Unterschied der Halbsehnen für 89,9° läßt sich aber nicht mehr unterscheiden von der für 90°. Aber die Strecke des Cosinus hat jetzt ihren größten Unterscheid. Man rechnet daher nach Pythagoras den Sinus in diesem Bereich aus dem Cosinus um. So ähnlich werden die ersten Winkelfunktionstabellen entstanden sein. Zeit hatten die Altvorderen ja genug, um das alles mit der Hand zu konstruieren, zu messen und zu berechnen.
| Winkel (°) | Sinus (mm) | Cosinus (mm) |
|---|---|---|
| 0,1 | 1,7 | 1000,0 |
| 0,2 | 3,5 | 1000,0 |
| 0,3 | 5,2 | 1000,0 |
| 0,4 | 7,0 | 1000,0 |
| 0,5 | 8,7 | 1000,0 |
| 0,6 | 10,5 | 999,9 |
| 0,7 | 12,2 | 999,9 |
| 0,8 | 14,0 | 999,9 |
| 0,9 | 15,7 | 999,9 |
| 1,0 | 17,5 | 999,8 |
| … | … | … |
| 89,0 | 999,8 | 17,5 |
| 89,1 | 999,9 | 15,7 |
| 89,2 | 999,9 | 14,0 |
| 89,3 | 999,9 | 12,2 |
| 89,4 | 999,9 | 10,5 |
| 89,5 | 1000,0 | 8,7 |
| 89,6 | 1000,0 | 7,0 |
| 89,7 | 1000,0 | 5,2 |
| 89,8 | 1000,0 | 3,5 |
| 89,9 | 1000,0 | 1,7 |
| 90,0 | 1000,0 | 0,0 |
Wie die griechischen und arabischen Astronomen wirklich zu den Funktionswerten kamen, habe ich auf der Seite Sinustabellen zusammengestellt. Den Höhepunkt hatten die Tabellen bei Regimontanus (Sinuswertetabelle). Dann kam John Napier auf die Idee, "künstliche" Sinusse zu verwenden (das war die Einführung der Logarithmen). Die Logarithmen bedeuteten auch das Ende der Prosthaphaerese, mit der bis dahin Multiplikationen von Sinuswerten durch Additionen der halben Winkel ersetzt worden waren.
Einen Fortschritt brachten erst die Reihenentwicklungen der Winkelfunktionen von Brook Taylor, die eine direkte Berechnung ohne mühevolle Tabellenberechnungen und Rundungsfehler erlaubt.
Gibt man den Winkel im Bogenmaß des Einheitskreises an![]() ,
,
so lautet die Formel der Taylorschen Reihe für den Sinus:
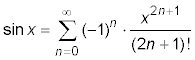
und für den Cosinus:
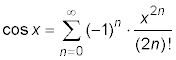
Zur Berechnung setzt man in die Formel nacheinander für n die Werte 0, 1, 2, … und für x den gewünschten Winkel ein. Das Vorzeichen des jeweiligen Reihenglieds ergibt sich aus der Potenz von (-1): (-1)0 = +1, (-1)1 = -1, (-1)2 = +1, usw. Sehen wir uns einmal an, was herauskommt.
| α° | n | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 5 | 8,73·10-2 | -1,11·10-4 | 4,22·10-8 | -7,65·10-12 | 8,09·10-16 | -5,60·10-20 | 2,73·10-24 | -9,91·10-29 | 2,78·10-33 | -6,18·10-38 | 1,12·10-42 |
| 10 | 1,75·10-1 | -8,86·10-4 | 1,35·10-6 | -9,79·10-10 | 4,14·10-13 | -1,15·10-16 | 2,24·10-20 | -3,25·10-24 | 3,64·10-28 | -3,24·10-32 | 2,35·10-36 |
| 15 | 2,62·10-1 | -2,99·10-3 | 1,02·10-5 | -1,67·10-8 | 1,59·10-11 | -9,92·10-15 | 4,36·10-18 | -1,42·10-21 | 3,58·10-25 | -7,18·10-29 | 1,17·10-32 |
| 20 | 3,49·10-1 | -7,09·10-3 | 4,32·10-5 | -1,25·10-7 | 2,12·10-10 | -2,35·10-13 | 1,83·10-16 | -1,06·10-19 | 4,77·10-23 | -1,70·10-26 | 4,93·10-30 |
| 25 | 4,36·10-1 | -1,38·10-2 | 1,32·10-4 | -5,97·10-7 | 1,58·10-9 | -2,73·10-12 | 3,34·10-15 | -3,03·10-18 | 2,12·10-21 | -1,18·10-24 | 5,34·10-28 |
| 30 | 5,24·10-1 | -2,39·10-2 | 3,28·10-4 | -2,14·10-6 | 8,15·10-9 | -2,03·10-11 | 3,57·10-14 | -4,66·10-17 | 4,70·10-20 | -3,77·10-23 | 2,46·10-26 |
| 35 | 6,11·10-1 | -3,80·10-2 | 7,09·10-4 | -6,30·10-6 | 3,26·10-8 | -1,11·10-10 | 2,65·10-13 | -4,71·10-16 | 6,46·10-19 | -7,04·10-22 | 6,26·10-25 |
| 40 | 6,98·10-1 | -5,67·10-2 | 1,38·10-3 | -1,60·10-5 | 1,09·10-7 | -4,81·10-10 | 1,50·10-12 | -3,49·10-15 | 6,25·10-18 | -8,91·10-21 | 1,03·10-23 |
| 45 | 7,85·10-1 | -8,07·10-2 | 2,49·10-3 | -3,66·10-5 | 3,13·10-7 | -1,76·10-9 | 6,95·10-12 | -2,04·10-14 | 4,63·10-17 | -8,35·10-20 | 1,23·10-22 |
| 50 | 8,73·10-1 | -1,11·10-1 | 4,22·10-3 | -7,65·10-5 | 8,09·10-7 | -5,60·10-9 | 2,73·10-11 | -9,91·10-14 | 2,78·10-16 | -6,18·10-19 | 1,12·10-21 |
| 55 | 9,60·10-1 | -1,47·10-1 | 6,79·10-3 | -1,49·10-4 | 1,91·10-6 | -1,60·10-8 | 9,44·10-11 | -4,14·10-13 | 1,40·10-15 | -3,78·10-18 | 8,29·10-21 |
| 60 | 1,05 | -1,91·10-1 | 1,05·10-2 | -2,74·10-4 | 4,17·10-6 | -4,16·10-8 | 2,92·10-10 | -1,53·10-12 | 6,16·10-15 | -1,97·10-17 | 5,16·10-20 |
| 65 | 1,13 | -2,43·10-1 | 1,57·10-2 | -4,80·10-4 | 8,58·10-6 | -1,00·10-7 | 8,28·10-10 | -5,07·10-12 | 2,40·10-14 | -9,04·10-17 | 2,77·10-19 |
| 70 | 1,22 | -3,04·10-1 | 2,27·10-2 | -8,06·10-4 | 1,67·10-5 | -2,27·10-7 | 2,17·10-9 | -1,54·10-11 | 8,46·10-14 | -3,69·10-16 | 1,31·10-18 |
| 75 | 1,31 | -3,74·10-1 | 3,20·10-2 | -1,31·10-3 | 3,11·10-5 | -4,84·10-7 | 5,32·10-9 | -4,34·10-11 | 2,73·10-13 | -1,37·10-15 | 5,59·10-18 |
| 80 | 1,40 | -4,54·10-1 | 4,42·10-2 | -2,05·10-3 | 5,56·10-5 | -9,85·10-7 | 1,23·10-8 | -1,14·10-10 | 8,19·10-13 | -4,67·10-15 | 2,17·10-17 |
| 85 | 1,48 | -5,44·10-1 | 5,99·10-2 | -3,14·10-3 | 9,59·10-5 | -1,92·10-6 | 2,71·10-8 | -2,84·10-10 | 2,30·10-12 | -1,48·10-14 | 7,74·10-17 |
| 90 | 1,57 | -6,46·10-1 | 7,97·10-2 | -4,68·10-3 | 1,60·10-4 | -3,60·10-6 | 5,69·10-8 | -6,69·10-10 | 6,07·10-12 | -4,38·10-14 | 2,57·10-16 |
Wir erkennen, bei kleinen Winkeln nimmt der Wert der Reihenglieder rasch ab: sie konvergiert schnell. Bei Winkeln nahe 90° ist die Konvergenz geringer. Wenn wir also den Sinuswert eines Winkels auf 3 Kommastellen berechnen wollen, reichen bei Winkeln bis 10° die ersten beiden Reihenglieder (n = 0 und 1), ab 80° müssen wir schon vier Glieder berechnen. Mehr Kommastellen für den Sinuswert verursachen beträchtlichen Aufwand — jedenfalls bevor die Computer erfunden wurden.
Nach diesen Reihenentwicklungen rechnen alle Computer. Die Taschenrechner und PC-Programme unterscheiden sich nur in der Anzahl Reihenglieder, die berechnet werden (und damit in der Stellenzahl des Winkelfunktionswertes). Mein Taschenrechner (Casio fx 992s) zeigt 12 Stellen an, und bricht wohl nach 3 Reihengliedern bei kleinen und nach 9 Gliedern bei großen Winkeln ab. MS-Excel gibt an, auf 17 Stellen zu rechnen (das sind 16 Stellen nach dem Komma). Es bricht bei α = 85° erst nach 10 Reihengliedern ab, bei 5° schon nach 5 Gliedern, wie man leicht nachprüfen kann.
|
|
© Rainer Stumpe URL: http://www.rainerstumpe.de |