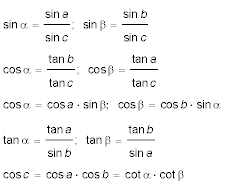Sphärische Trigonometrie
Sätze im sphärischen Dreieck
Der Seitensinussatz
|
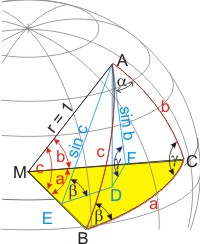
Um Rechenregeln für das Dreieck ABC abzuleiten, fällen wir das Lot von C auf die Ebene MAB (Fußpunkt D) und die Lote von C auf die Strecke MA (Fußpunkt E) und MB (Fußpunkt F). Setzt man den Kugelradius gleich 1, so ist die Länge der Strecke CE gleich sin b (Gegenkathete zum Winkel b im rechtwinkliges Dreieck CME) und die Länge der Strecke CF ist gleich sin a (Gegenkathete zum Winkel a im rechtwinkliges Dreieck CMF). Da a, b und c auf Großkreisen liegen, sind die Winkel BMC = a, AMC = b und AMB = c (a, b, c im Bogenmaß). |
|
|
Die Lote haben ebene Dreiecke erzeugt, in denen genügend Größen bekannt sind, um die übrigen zu berechnen. Für die Länge des Lotes CD können wir zwei Ausdrücke finden: CD ist die Gegenkathete zu α im Dreieck CDE und die Gegenkathete zu β im Dreieck CDF. CD = sin α · sin b = sin β · sin a; die Gleichung teilen wir durch sin β und sin a und erhalten:
Mit dem gleichen Formalismus und den Loten auf die Ebenen AMC bzw. BMC den Sinussatz: sin a : sin b : sin c = sin α : sin β : sin γ |
|
Der Seitencosinussatz
|
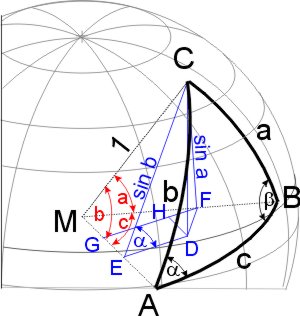
Im Dreieck CEM sind bekannt der Winkel <CME und die Hypotenuse = 1. Die Strecke EM (Ankathete zu <b) erhalten wir aus der Definition des Cosinus cos b = ME. Ebenso ist MF = cos a. Fällen wir das Lot von F auf AM (Fußpunkt G), erhalten wir ein ebenes Dreieck MFG, in dem der Winkel <c und die Hypotenuse bekannt sind. Für die Länge der Strecke GM erhalten wir cos c = GM / cos a => GM = cos c · cos a. Fällen wir nun das Lot von D auf FG (Fußpunkt H), so erhalten wir ein Dreieck DFH, in dem der Winkel <DFH = c (die Schenkel stehen paarweise senkrecht aufeinander) ist. |
|
In diesem Dreieck ist die Länge der Hypotenuse DF aus dem Dreieck CDF zu berechnen: cos β = DF / sin a =>
DF = sin a · cos β. Damit ist die Länge DH durch Umformen aus sin c = DH / (sin a · cos β) =>
DH = sin c · sin a · cos β. Dasselbe Spiel für die Ebenen ACM und BCM führt zu den anderen beiden Gleichungen des Seitencosinussatzes: |
|
|
cos a = cos b · cos c + sin b · sin c · cos α, cos b = cos c · cos a + sin c · sin a · cos β, cos c = cos a · cos b + sin a · sin b · cos γ. |
|
Der Winkelcosinussatz
Der Winkelcosinussatz kann auf ähnliche Weise wie der Seitencosinussatz abgeleitet werden. Da man in der Navigation nicht braucht, verzichten wir hier.
cos β = - cos γ · cos α + sin γ · sin α · cos b
cos γ = - cos α · cos β + sin α · sin β · cos c
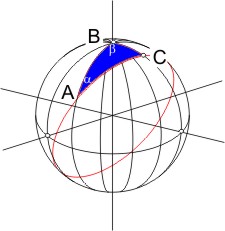
Das rechtwinklige sphärische Dreieck
|
So wie das Rechnen im rechtwinkligen ebenen Dreieck einfacher ist, ist auch das Rechnen im rechtwinkligen sphärischen Dreieck einfacher. Für die Navigation auf dem Großkreis erzeugt man deshalb ein rechtwinkliges Dreieck, indem man vom Nordpol aus das Lot auf den Großkreis fällt, auf dem man fahren will (Kurs-Großkreis). Der Schnittpunkt C des Lotes mit dem Großkreis, der dem Nordpol am nächsten liegt heißt "Scheitel S". Im Dreieck ABC ist also der Winkel γ bei C ein rechter (γ = 90°). |
Im rechtwinkligen Dreieck gelten vereinfachte Beziehungen für die Seiten und Winkel:
Merken kann man sich diese Formeln mit der Neperschen Regel.
Dies wird ausgenutzt, um bei der Großkreisnavigation
Wegpunktkoordinaten
und Kurswinkel auszurechnen. Für die Breitenkoordinaten φWP des Wegpunktes A bei gegebener Länge
λWP lautet die Formel:
Es bleibt die Frage der Berechnung der Scheitelkoordinaten aus den Ortskoordinaten von Start und Ziel.
Die Breite φS des Scheitels ist 90° - a, und a erhalten wir bei bekanntem Winkel α
und Seite c
aus sin α = sin a/sin c => cos φS = sin α · cos φA. Der Winkel β
entspricht dem Längenunterschied von A und S = λA - λS.
Aus der Beziehung cos c= cot α · cot β =>
tan (λA - λS) = 1/(sin φA · tan
α).
Mit bekannter Länge des Scheitels lässt sich so die Länge eines Wegpunktes berechnen.
Der Winkel, unter dem der Großkreis einen Meridian φ schneidet, ergibt sich aus der Gleichung
sin α = sin a/sin c => sin α · = cos φS/cos φWP.
Damit sind die Formeln des sphärischen Dreiecks für die Navigation abgeleitet.
|
|
© Rainer Stumpe URL: http://www.rainerstumpe.de |