Sphärische Trigonometrie
Einführung
Die Geometrie der Dreiecke auf der Kugeloberfläche hat viele Analogien mit der Trigonometrie in der Ebene, die wesentlich von Euklid zusammengefaßt worden ist. So finden die Geraden in der Ebene ihre Entsprechung in den Kreisen auf der Kugeloberfläche, deren Mittelpunkt mit dem Kugelmittelpunkt zusammenfält (Großkreise). Großkreise werden durch zwei Punkte eindeutig bestimmt, das Großkreissegment zwischen den beiden Punkten ist die kürzeste Entfernung und Kugeldreiecke werden durch die Schnittpunkte dreier Großkreise gebildet. Anders als Geraden in der Ebene haben Großkreise aber eine endliche Länge (den Kugelumfang), es gibt keine parallelen Großkreise und die Winkelsumme im sphärischen Dreieck ist größer als 180° (2·π) aber kleiner als 540° (6·π).
Da eines der Axiome der Euklidischen Geometrie — das Parallelenaxiom — nicht gilt, ist die sphärische Geometrie ein Beispiel für eine nicht-Euklidischen Geometrie.
Da bereits die griechischen Astronomen und Mathematiker von einer kugelförmigen Erde und einer Himmelskugel ausgegangen sind, liegt es nahe, dass sie sich mit der Geometrie auf der Kugeloberfläche auseinander gesetzt haben. Nach [1] stammt die älteste Schrift zur Kugelgeometrie ("Über die sich bewegende Kugel") von Autolykos (330 v. Chr.). Von Menelaos (um 100 n. Chr.) wird erstmals das Kugeldreieck diskutiert. Indische und arabische Astronomen forschten auf dem Gebiet, und um das Jahr 1000 entdeckten arabische Mathematiker den Sinussatz und lösten alle Augaben im sphärischen Dreieck.
Die Wiener Mathematiker Georg von Peurbach und Regiomontanus griffen die griechischen und arabischen Schriften zur Kugelgeometrie wieder auf. Regiomontanus schrieb seine Forschungen in fünf Büchern "De triangulis" zusammen (1462-1464), und gab damit wesentliche Impulse für die Entwicklung der Wissenschaften in der Renaissance.
Der schottische Mathematiker John Napier (latinisiert Neper(ius)) veröffentlichte 1614 ein Lehrbuch ("Mirifici Logarithmorum Canonis Constructio") zur Berechnung der Gleichungen in der sphärischen Trigonometrie, wozu er die Logarithmen der Winkelfunktionen einführte. Sein Schüler Edmung Gunter schrieb 1623 das erste Buch in englischer Sprache zur Verwendung der sphärischen Trigonometrie und der Logarithmen der Sinus- und Cosinuswerte in der Navigation. Es wurde als Standardlehrbuch von der englischen Marine eingeführt, und erschien in vielen — auch von Dritten überarbeiteten und ergänzten — Auflagen. Damit war die sphärischen Trigonometrie im Kanon der Bildung angekommen. Sie blieb ein Bestandteil der Allgemeinbildung bis kurz vor dem Beginn meiner Gymnasialzeit.
Grundlagen
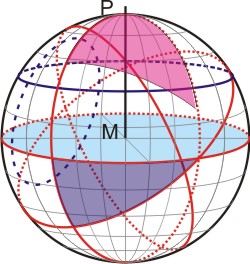
Im Bild rechts sind Kreise auf der Kugeloberfläche eingezeichnet. Zwei Arten Kreise werden unterschieden: Kreise, die den Kugelmittelpunkt M auch zu ihrem Mittelpunkt haben, nennt man Großkreise (rot). Alle anderen sind Kleinkreise (blau). Ein Großkreis entsteht, wenn man eine Kugel in zwei gleich große Hälften teilt. Das Lot auf der Ebene dieses Großkreises durchstößt die Kugel im Pol P. Alle Großkreise, die durch den Pol gehen (Meridiane) schneiden den halbierenden Großkreis (Äquator) im rechten Winkel. Die Ebene des Großkreises und der Pol bilden das Koordinatensystem, das Navigatoren kennen.
Drei Großkreise bilden ein sphärisches (Kugel-)Dreieck. (Da es keine parallelen Großkreise gibt, muß aus drei Großkreisen ein Kugeldreieck entstehen.) Ein sphärisches Dreieck aus dem Äquator und zwei Meridianen hat eine Winkelsumme von mindestens 180°, da die Meridiane beide den Äquator mit einem Winkel von 90° schneiden, hinzu kommt im sphärisches Dreieck der Winkel, den die Meridiane am Pol einschließen. Dieser Winkel kann — in einem Eulerschen Kugeldreieck — maximal 180° betragen. Das so gebildete Dreieck hat also eine Winkelsumme von 360°. Folgende Sätze gelten im sphärischen Dreieck:
- Ein sphärisches Dreieck kann mit seinem Gegendreieck nur dann zur Deckung gebracht werden, wenn es zwei gleiche Seiten hat.
- Im sphärischen Dreieck liegen gleiche Seiten gleichen Winkeln gegenüber.
- Im sphärischen Dreieck liegt der größten Seite der größte Winkel gegenüber.
- Im sphärischen Dreieck ist eine Seite kleiner als die Summe der beiden anderen.
- Im sphärischen Dreieck ist die Summe der drei Seiten kleiner als 360°.
- Im sphärischen Dreieck ist die Summe der drei Winkel größer als 360° und kleiner als 540°.
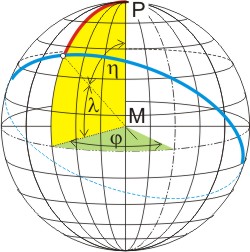 Etwas ungewohnt an der sphärischen Trigonometrie ist, dass in den Formeln nicht nur die Dreieckswinkel, sondern auch die Dreiecksseiten in Bogengrad angegeben werden. (Zur Unterscheidung werden Dreieckswinkel mit kleinen griechischen Buchstaben bezeichnet, die Dreiecksseiten mit kleinen lateinischen.) Das ist möglich durch die Verwendung des Bogenmaßes auf einer Kugel mit dem Radius 1. Die Länge eines Kreissegments auf einem Großkreis entspricht dann dem Winkel, unter dem man den Bogen vom Mittelpunkt aus sieht. Der rote Bogen im Bild links ist also η° lang. Gemessen wird in der Ebene des Großkreis (hier gelb). Auf der Erdkugel wäre er η° · 60 Seemeilen lang. Auf anderen Kugeln mit dem Durchmesser d [km] wäre er (η° ⁄ 360°) ·π · d [km] lang.
Etwas ungewohnt an der sphärischen Trigonometrie ist, dass in den Formeln nicht nur die Dreieckswinkel, sondern auch die Dreiecksseiten in Bogengrad angegeben werden. (Zur Unterscheidung werden Dreieckswinkel mit kleinen griechischen Buchstaben bezeichnet, die Dreiecksseiten mit kleinen lateinischen.) Das ist möglich durch die Verwendung des Bogenmaßes auf einer Kugel mit dem Radius 1. Die Länge eines Kreissegments auf einem Großkreis entspricht dann dem Winkel, unter dem man den Bogen vom Mittelpunkt aus sieht. Der rote Bogen im Bild links ist also η° lang. Gemessen wird in der Ebene des Großkreis (hier gelb). Auf der Erdkugel wäre er η° · 60 Seemeilen lang. Auf anderen Kugeln mit dem Durchmesser d [km] wäre er (η° ⁄ 360°) ·π · d [km] lang.
Denn — der Navigator erinnert sich — die Seemeile ist als Bogenminute auf einer Kugel mit dem mittleren Erddurchmesser definiert. Das macht Entfernungsangaben in Seemeilen einfach: man braucht nur die Großkreisbogenlänge zu bestimmen.
Zur Bestimmung von Entfernungen und Richtungen gibt es in der sphärischen Trigonometrie wie in der ebenen Rechenregeln und Formeln. Wie in der ebenen Trigonometrie gibt es für das Kugeldreieck Vereinfachungen beim rechtwinkligen Dreieck, außerdem gibt es noch das Poldreieck, in dem einige Formeln übersichtlicher werden. Die Formeln werden in der terrestrischen Navigation und besonders in der Astronavigation verwendet.
- Zum Thema gehörende Seiten:
- [sphärische Trigonometrie - Grundlagen]
- [Das rechtwinklige sphärische Dreieck]
- [Das schiefwinklige sphärische Dreieck]
- [Anwendungen der sphärische Trigonometrie] (Orthodrome, Tageslänge, Deklination der Sonne)
- [Anwendungen der sphärische Trigonometrie] (Sonnenhöhe, indischer Kreis)
- [Die Nepersche Regel]
- [Beispielrechnung]
- [Konstruktion mit Projektion der Kugel]
Quellen
- Lambacher-Schweitzer (Hg.), Mathematisches Unterrichtswerk, Teil III/3: Kugelgeometrie, Ernst Klett Verlag, Stuttgart 1951.
- Helmut Gericke: Mathematik in Antike, Orient und Abendland. Fourier Verlag, 2003.
- Brockhaus Enzyklopädie, 20. Auflage, Mannheim 1998.
- H. Kößlinger: Ebene und sphärische Trigonometrie. Franz Ehrenwirth Verlag, München 1948
Biografische Notitzen
- Autolykos von Pitane
- griech Astronom und Mathematiker, * um 360 v. Chr. in Pitane (Äolien) , † um 290 v. Chr. Älterer Zeitgenosse Euklids; untersuchte die Kugelgeometrie als Werkzeug der Astronomie und der Zeitmessung.
- Leonard Euler
- Schweizer Mathematiker, * 15. Apr 1707 in Basel, † 18. Sep 1783 in Sankt Petersburg. Auf ihn geht u. a. die in der Mathematik verwendete Symbolik zurück; er schränckte bei seinen Berechnungen der Fläche des Kugeldreiecks den größten Winkel auf kleiner als 180° ein.
- Menelaos von Alexandria
- griech. Astronom und Mathematiker, * um 70 in Alexandria, † um 140 in Rom. Sein Werk Spaerica ist in arabischer Sprache erhalten und behandelt die Kugelgeometrie und die spärische Trigonometrie; ein anderes Werke ("Elementa Geometricae") ist verloren.
- Regiomontanus
- Johannes Müller (latinisiert: Molitoris), genannt "der Königsberger" (latinisiert: Regiomontanus; geb. 6. Jun. 1436 in Königsberg (OT Unfinden, Unterfranken), † 8. Jul 1476 in Rom. dt. Astrologe, Astronom und Mathematiker. Gab Ephemeriden heraus, die von u. a. Christopher Columbus, Vasco da Gama, Amerigo Vespucci benutzt wurden. Das Hauptwerk De triangulis erschien posthum im Jahr 1533, war aber wohl aus Briefewechseln bekannt.