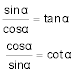Die Winkelfunktionen
Definitionen der Winkelfunktionen
Wenn man alle möglichen Dreiecke berechnet hat, dann erkennt man einen Zusammenhang zwischen dem Winkel und seiner gegenüberliegenden Seite: je größer der Winkel, desto länger ist die gegenüberliegende Dreiecksseite. Der Zusammenhang zwischen Winkel und seiner gegenüberliegenden Seite ist eine Funktion (im hier verwendeten Sinne eine mathematische Rechenvorschrift). Aus historischen Gründen werden die Winkelfunktionen am rechtwinkligen Dreieck abgeleitet. Im rechtwinkligen Dreieck heißt die dem rechten Winkel gegenüberliegende Seite Hypotenuse, die beiden anderen Seiten sind die Katheten. Hier unterscheidet man die Ankathete (b ist Ankathete zum Winkel α) und Gegenkathete (a ist Gegenkathete zum Winkel α).
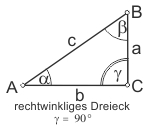
- das Verhältnis der Gegenkathete a zur Hypotenuse c heißt Sinus von α: sin α = a ⁄ c;
- das Verhältnis der Ankathete b zur Hypotenuse c heißt Cosinus von α: cos α = b ⁄ c
- das Verhältnis der Gegenkathete a zur Ankathete b heißt Tangens von α: tan α = a ⁄ b;
- das Verhältnis der Ankathete b zur Gegenkathete a heißt Cotangens von α: cot α = b ⁄ a.
Historische Winkelfunktionen
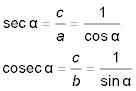
In alten Büchern findet man noch zwei weitere Winkelfunktionen: Secans (sec) und Cosecans (cosec). Es sind das die Kehrwerte von Sinus bzw. Cosinus.
Und zur Vereinfachung der Berechnungen im schiefwinkligen Dreieck gab es Tabellen des sinus versus (versin) seiner halben Werte (Haversine). Die geometrische Erklärung wird im Zusammenhang mit den Sinustabellen gegeben.
- versine α = 1 - cos α,
- haversine α = ½ · (1 - cos α).
- haversine α = ½ · (1 - cos α) = [(s - b) · (s - c)] ⁄ (b · c)
- dabei ist s = a + b + c.
Beziehungen der Winkelfunktionen
Die Winkelfunktionen des gleichen Winkels stehen zu einander in Beziehungen. Man kann die leicht ableiten, wenn man den Satz des Pythagoras anwendet: a2 + b2 = c2. Setzt man für
- a2 =(c · sin α)2
- b2 = (c · cos α)2
- c2 = 12 = 1,
- erhält man
- sin2 α + cos2 α = 1
Da im rechtwinkligen Dreieck außerdem α + β = 90° gilt und die Phasenbeziehung der Winkelfunktionen sagt sin α = cos (90° - α), ist die Beziehung der Winkelfunktionen auch sin2 α + sin2 β = 1. Nach dem gleichen Formalismus erhält man:
- a2 =(c · sin α)2
- b2 = (c · sin β)2
- sin2 α = 1 - sin2 β.
Radiziert man diese letzte Formel erhält man:
- sin α = √(1 - sin2 β)
damit hat man eine einfache Beziehung für die Berechnung der Stücke des rechtwinkligen Dreiecks mit einem Rechenschieber, der eine "pythagoreische" Skala mit Werten von √(1 - sin2 β) trägt. Solche Rechenschieber sind vom System Darmstadt.
Tangens und Cotangens
Durch Division der Winkelfunktionen erhält man:
Mit diesen beiden Gleichungen kann man nun jede Funktion des Winkels α durch die anderen Funktionen ausdrücken:
|
|
||||||
| sin α |
|
|
|
|||
|
|
||||||
| cos α |
|
|
|
|||
|
|
||||||
| tan α |
|
|
|
|||
|
|
||||||
| cot α |
|
|
|
|||
|
|
||||||
Zwischen den Funktionen der Nebenwinkel (deren Summe ja 180° beträgt) gelten im rechtwinkligen Dreieck wegen β = 90° - α die Beziehungen:
- sin α = cos(90° - α)
- cos α = sin(90° - α)
- tan α = cot(90° - α)
- cot α = tan(90° - α)
Die Paare Sinus und Cosinus und Tangens und Cotangens werden jeweils Kofunktionen von einander genannt.
Jede Funktion eines spitzen Winkels ist gleich der Kofunktion seines Nebenwinkels.
Für die Benennung des Sinus gibt es zwei Erklärungen.
- Sinus ist die Abkürzung des lateinischen Ausdrucks semis inscriptae = halbe Kreissehne;
- Das arabische Wort für Sehne (dschiba) wurde verwechselt mit dem arabischen Wort dschaib (Bucht) und ins lateinischen mit sinus (Bucht) übersetzt.
Die Umkehrfunktionen
Die Winkelfunktionen geben die Länge einer Dreiecksseite in Abhängigkeit von Dreieckswinkeln an. Nun kann man am Rechenschieber leicht ablesen, welcher Winkel zu einer Seitenlänge gehört. Um aber mit Gleichungen rechnen zu können (z. B. auf dem Computer), benötigt man eine Funktion, die den Winkel aus einer Seitenlänge berechnet. Diese Funktionen nennt man Umkehrfunktionen der Winkelfunktionen. Sie heißen Arcussinus (arcsin), Arcuscosinus (arccos), Arcustangens (arctan) und Arcuscotangens (arccot; wird häufig nicht von Softwareprogrammen angeboten, da cot = 1 ⁄ tan). Softwareprogramme rechnen intern im Bogenmaß, sodass das Ergebnis der Umkehrfunktionen in Bruchteilen des Umkreisumfangs angegeben wird. Zur Umrechnung in das Winkelmaß wird diese Zahl mit 360° ⁄ 2 · π multipliziert.
|
|
© Rainer Stumpe URL: http://www.rainerstumpe.de |