Grundlagen des Rechenschiebers

Die höheren Rechenarten

Für das Rechnen mit Zahlen gibt es neben den Grundrechenarten:

• Addieren: 7 + 2 = 9
• Subtrahieren: 7 - 2 = 5
• Multiplizieren: 7 · 2 = 14
• Dividieren: 7 : 2 = 3 ½

die höheren Rechenarten. Das sind:

• Potenzieren: 7² = 7 · 7 = 49

und seine beiden Umkehrungen

• Radizieren (Wurzelziehen):
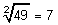
• und Logarithmieren: ¹⁰lg(7) = 0,8451.

Der Rechenschieber wird eingesetzt zum Multiplizieren, Dividieren, Potenzieren, Radizieren und Lo­ga­ri­th­mieren. (Es gibt aber Sonderausgaben, die auf der Rückseite zusätzlich einen "Addiator" für ganz faule anbieten.) Für die Infinitesimalrechnung, die ebenfalls zu den "höheren Rechenarten" gehört, gibt es keine Rechenschieberanwendung — sie stammt aus der analytischen Geometrie.

Rechnen mit Potenzen

Der Potenzausdruck 7² wird gelesen "sieben hoch zwei" oder "sieben zum Quadrat". Er ist die Kurz­fas­sung der Rechenvorschrift: 7 · 7. Der Ausdruck 3⁵ wäre dann die Kurzfassung von 3 · 3 · 3 · 3 · 3 = 243. In diesen Ausdrücken nennt man die auf der Zeile stehende Zahl "Basis", und die hochgestellte "Ex­po­nen­ten".  Für das Multiplizieren und Dividieren mit Potenzen gibt es Regeln, falls die Basen oder die Ex­po­nen­ten gleich sind. Potenzen mit ungleichen Base und Exponenten muss man einzeln berechnen. Per de­fi­ni­tio­nem ist 5⁰ = 1 (Jede beliebig große Zahl mit dem Exponenten Null ist gleich 1).

1. Gleiche Basis:
   • a^m · aⁿ = a^(m + n), z. B.
     5² · 5³ = 5 · 5 · 5 · 5 · 5 = 5⁵ = 3125;
   • und:
   • a^m : aⁿ = a^(m - n), z. B.
     5³ : 5² = (5 · 5 · 5) : (5 · 5) = 5¹ = 5;.
2. Gleicher Exponent:
   • aⁿ · bⁿ = (a · b)ⁿ, z. B.
     3³ · 5³ = 3 · 3 · 3 · 5 · 5· 5 = 3375 = 15³;.
   • und:
   • aⁿ : bⁿ = (a : b)ⁿ 3³ : 5³ = (3 · 3 · 3) : (5 · 5 · 5) = 0,216 = (3 : 5)³.
3. Negative Exponenten (Bei diesen Rechnungen können negative Exponenten auftreten!):
   • a ^- n = ¹ ⁄ _aⁿ, z. B.
     5² : 5³ = 5^-1 = 1 : 5 = ¹ ⁄ ₅ = 0,2;.
4. Potenzen von Potenzen:
   • (a^m)ⁿ = a^(m · n), z. B.
     (5²)³ = (5 · 5)³ =  (5 · 5) ·(5 · 5) ·  (5 · 5) = 15625 = 5⁶.

Umkehrung: Radizieren

Eine der beiden Umkehrungen des Potenzierens ist das Wurzelziehen, symbolisiert mit dem Wur­zel­zeichen . Es wird gelesen "dritte Wurzel aus 125". Das Ergebnis ist die Zahl x, deren dritte Potenz 125 ergibt 125 = x³, also x = 5. Vereinbarungsgemäß lässt man die 2 bei der Quadratwurzel weg: .

In Exponentialschreibweise des Wurzelziehens schreibt man gebrochene Exponenten:

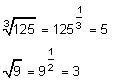
Umkehrung: Logarithmieren

Wenn man mit Potenzzahlen zur gleichen Basis das Multiplizieren durch eine Addition der Exponenten ersetzen kann, müsste man nur jede beliebige Zahl durch eine Potenz (zur gleichen Basis) ersetzen und könnte die Multiplikation durch die (manuell) leichtere Addition ersetzen. Das war die Überlegung hinter der Entwicklung der Logarithmen. Die Frage lautet also: Welchen Exponenten m zur Basis 2 hat die Zahl 128, welchen Exponenten n hat die Zahl 512? Dann lässt sich 128 · 512 rechnen als 2^(m + n). (Da jede Zahl mit dem Exponenten 0 gleich 1 ist, ist der Logarithmus von 0 unbestimmt.)

• 128 · 512 = 2⁷ · 2⁹ = 2¹⁶ = 65.536.

Analog den Rechenregeln für Potenzzahlen gilt für Logarithmen:

• log (a · b) = log a + log b
• log (^a/_b) = log a - log b

Für die Multiplikation bzw. Division der Zahlen a und b (in den Klammern) hat man eine Addition bzw. Subtraktion der Logarithmen der Zahlen a und b erreicht. Vor der Erfindung des Computers war da eine wesentliche Rechenerleichterung. (Wer noch "mit der Hand" multiplzieren und dividieren kann, wird das nachvollziehen.)

Anwendung der Logarithmen

Da man vor der Einführung der elektronischen Rechner die Frage nach dem Logarithmus einer be­lie­bi­gen Zahl x nur durch eine komplizierte Reihenberechnung — oder wie John Napier durch Berechnen einer geometrischen Reihe — beantworten konnte, wurden Tabellen angelegt, die Logarithmentafeln. In denen wurden alle (positiven) Zahlen x durch die Exponenten 1 zur Basis 10 aus­ge­drückt x = 10¹. In Symbolen ausgedrückt log₁₀ x = 1. Der Vorteil dieser quot;dekadischen" Logarithmen (solche zur Basis 10) ist, dass die Logarithmen einstellige Zahlen kleiner sind als 1, die 2-stelliger eine 1 vor dem Komma haben, 3-stel­lige eine 2, usw.

Um mit 5 signifikanten Stellen rechnen zu können, brauchte man 5-stellige Angaben der Logarithmen (Mantissen). Die Rechnung 128 · 512 mit einer Logarithmentafel sah so aus:

Man suchte die Mantissen von 128 und 512 aus der Tafel heraus und stellte die Zehnerpotenz vor das Komma:

• 128 ⇒ log(128) = 2,10721
• 512 ⇒ log(512) = 2,70927.
• 128 · 512 = log(128) + log(512) = 2,10721 + 2,70927 = 4,81648

Die Logarithmen der beiden Zahlen wurden addiert ⇒ 4,81648. Für die Nachkommazahl (Mantisse) wurde aus der Tafel die zugehörige Zahl herausgesucht 81648 → 65536 und die Ziffer vor dem Komma bestimmte die Zehnerpotenz (100 · 100 = 10.000 = 10⁴), also 128 · 512 = 65.536.

Neben den Logarithmen zur Basis 10 gibt es heute noch die "natürlichen Logarithmen" zur Basis e = 2,7182818284…, der Euler­schen Zahl, verwendet; sie heißen natürliche Logarithmen ln und werden für die For­mel­dar­stel­lung von Naturgesetzen verwendet. Ihr Vorteil ist, dass z. B. der radioaktive Atom­kern­zer­fall oder das Bak­te­rien­wachs­tum Gesetzmäßigkeiten folgen, die als Potenzen von e gehorchen.

Radioaktiver Zerfall: die Anzahl n radioaktiver Atome, die nach der Zeit t noch von anfänglich n₀ Atomen übrig geblieben sind, berechnet man nach:

dabei ist τ die Halbwertszeit, eine charakteristische Konstante für jedes radioaktive Isotop.

Nach Ablauf der Halbwertszeit t = τ sind noch vorhanden:

[Zurück]

Für das Rechnen mit nur drei oder vier signifikanten Stellen, also für das praktische Leben, reichte die Genauigkeit des Rechenschiebers. Mit ihm addiert und subtrahiert man Strecken geometrisch auf lo­ga­ri­thmisch eingeteilten Linearen. Den Logarithmus einer Zahl auf der logarithmischen Skala findet man auf der linearen Skala. log 3 = 0,477.

Man kann nun durch Addieren der Strecken auf der logarithmischen Skala eine Multiplikation aus­füh­ren. Dazu benutzt man zwei identische Skalen, die gegeneinander verschiebbar sind.

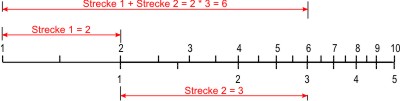
Das ist das Funktionsprinzip des Rechenschiebers.