Die Logarithmusskalen
Neben den Winkelskalen werden wir auch die Logarithmusskalen des Rechenschiebers brauchen (eine Anwendung ist die Zinseszinsrechnung). Verwendet werden die Skalen LL des natürlichen Logarithmus "ln". Da der Logarithmus zur Basis e = 2,71828… (Eulersche Zahl) die Zehnerpotenzen nicht im Kopf berechnen lässt, sind die Skalen LL aufgeteilt und überdecken einen Zahlenbereich von 0,01 bis 105.
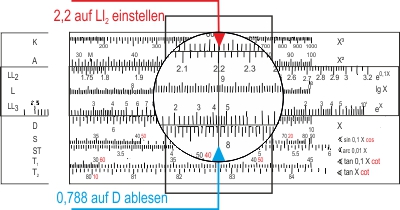
Um den ln 2,2 abzulesen, stellt man den Läufer auf der Skala LL2 über 2,2 und liest auf D den Wert ab: 0,788 (LL2 gibt e0,1x!).
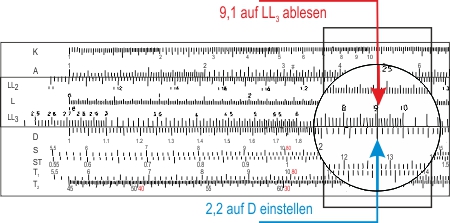
Zum Delogarithmieren, also um ex zu ermitteln, stellt man x = 2,2 auf D ein und liest den Wert der Potenz e2,2 = 9,1 auf LL3 ab.
Beispiel
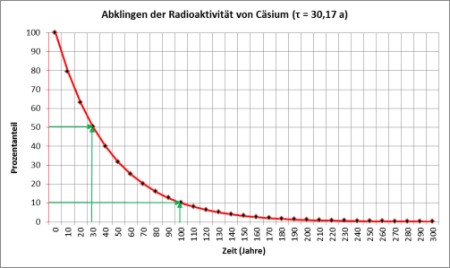
Als Beispiel für die Benutzung der Skalen LL2 und LL3 wollen wir berechnen, um wieviel die radioaktive Strahlung von 137Cäsium nach 20 (und weil's so einfach geht: nach 200) Jahren abgeklungen ist. Dazu verwenden wir die Formel:
Dabei ist die Halbwertszeit von 137Cäsium τ = 30,17 a (nach Wikipedia). Zur Berechnung brauchen wir einen Rechenschieber mit ex-Skalen. Auf den wenigsten Rechenschiebern gibt es zusätzliche e-x-Skalen, was nicht schlimm ist. Denn es gilt ja: e-x = 1/ex.
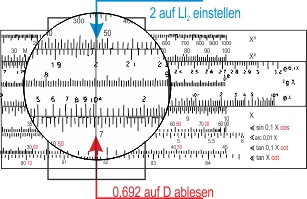
Den Exponenten der Formel berechnen wir zuerst. Und um Arbeit zu sparen in einer Reihenfolge von abwechselnder Multiplikation und Division. Als erstes bestimmen wir den Wert von ln 2.
Den Wert "2" finden wir auf der LL2-Skala. Wir schieben den Läfer auf den Wert und lesen auf der Skala D den wert ab: 0,692 (die LL2-Skala liefert e0,1 x Werte).
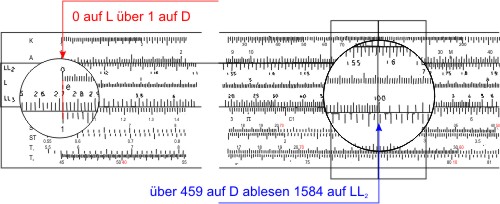
Diesen Wert dividieren wir durch die Halbwertszeit 30,17. Dazu muss die Zunge umgedreht werden, damit wir den Wert der Halbwertszeit 3017 auf der Skala C unter dem Läferstrich einstellen können. Unter der "1" auf der Skala C könnten wir das Ergebnis ablesen: 0,2298, brauchen wir aber nicht. Zum Multiplizieren mit 20 brauchen wir aber nur den Läufer auf die 2 auf der Skala C zu verschieben und den Zahlenwert des Exponenten auf D abzulesen: 0,459.
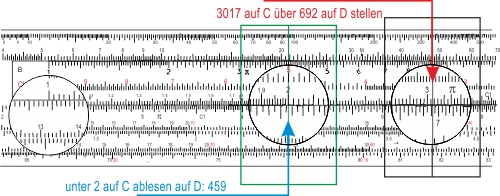
Nun müssen wir die Zunge wieder herumdrehen, dass wir die LL2-Skala sehen können. Wir stellen die "0" der L-Skala (dekadischer Logarithmus) über die "1" auf der Skala D, und lesen den Wert von e0,459 auf der LL2-Skala ab: 1,584
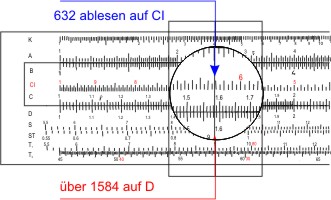
Zum Abschluß brauchen wir nur noch den Kehrwert zu bestimmen. Wir notieren 1,584 und drehen die Zunge wieder zurück. Über der 1,584 auf der Skala D lesen wir den Kehrwert auf der Skala CI (von rechts nach links) ab: 0,632.
Das Ergebnis: nach 20 Jahren (66,3 % der Halbwertszeit) sind noch 63,2 % der ursprünglichen Menge 137Cäsium vorhanden. Und nach 200 Jahren? Dazu brauchen wir in der Einstellung, in der wir den Wert der Exponentialfunktion auf LL2 ablasen nur auf LL3 (ex) abzulesen: 99 und den Kehrwert 0,0101 zu bilden: nach 200 Jahren ist nur noch 1% der ursprünglichen Menge 137Cäsium vorhanden.
[Zurück]
Finanzrechnungen
Eine besondere Stärke des Rechenschiebers liegt in Dreisatzaufgaben: man kann Tabellen generieren nur durch Verschieben des Läufers.
Zinsrechnung
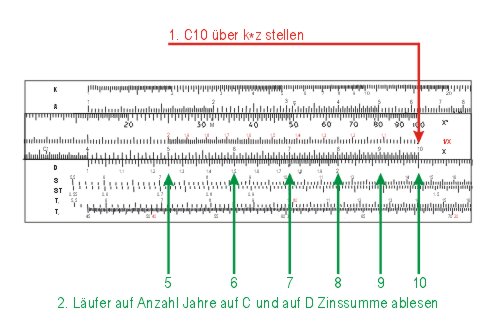
Bei einer (jährlichen) Verzinsung eines Kapitalbetrages k mit einem Zinssatz z über n Jahre berechnet man Zinsen nach der Zinsformel:
Bei 5.000 €, einem Zinssatz von 5 % und einer Anlage von 6 Jahren erhält man Zinsen in Höhe von 1.500 €. Auf dem Rechenschieber kann man mit der Einstellung k · z gleichzeitig auch den Zinsbetrag für beliebige Jahre ablesen (für 1-3 Jahre muss man die Zunge ´durchschieben).
[Zurück]
Zinses-Zinsrechnung
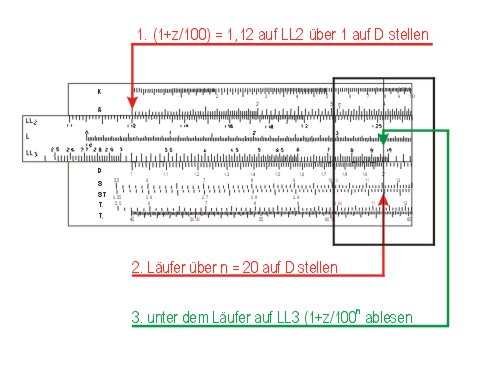
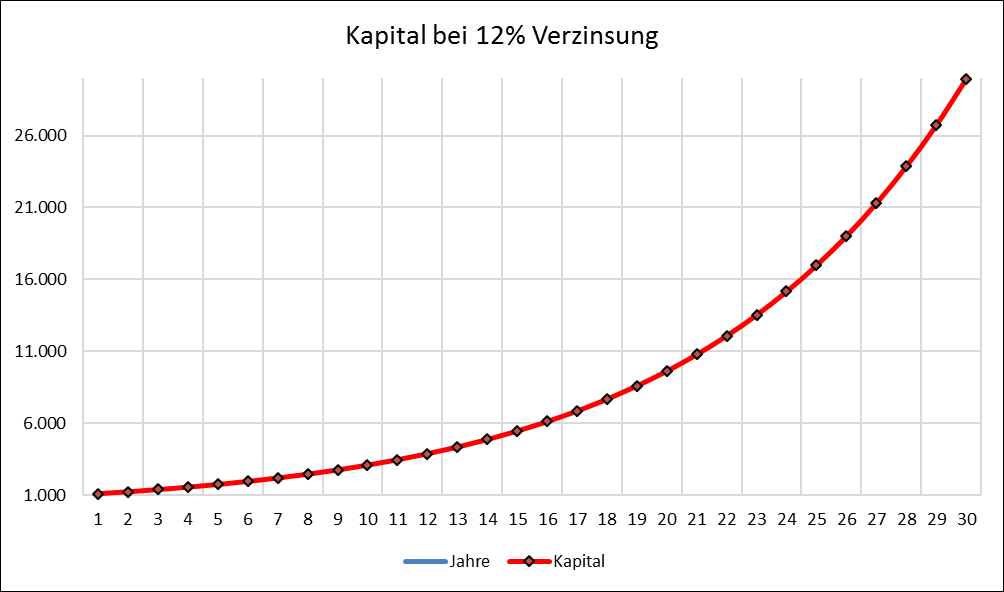
Lässt man die Zinsen stehen, so verzinsen sich die Zinsen ebenfalls: Das Kapital wächst schneller. Die Gleichung für die Kapitalmenge kn nach n = 20 Jahren mit einem Zinssatz z = 12 % bei einem Startkapital k0 = 100 lautet:
Zunächst berechnet man den Exponentialausdruck (1 + z ⁄ 100)n, dann schließt sich eine Multiplikation (auf C und D) dieses Faktors mit der Startsumme k0 an.
Der Faktor beträgt 9,65, das Kapital von 100 € hat sich auf 965 € verzinst. (Das waren noch Zeiten …) Nach 30 Jahren sind 1.000 € mit Zinseszins gar auf 29.960 € angewachsen.
[Zurück]