The Second Book of the Sector,
Containing the Use of the Circular Lines.

CHAPT. I.
Of the Nature of Sines, Chords, Tangents, and Secants, fit to be known before-hand, in reference to right-lined Triangles.

In the Canon of Triangles, a Circle is commonly divided into 360 Degrees, each Degree into 60 Minutes, each Minute into 60 Seconds.

• A Semicircle therefore is an Ark of 180 gr.
• A Quadrant is an Ark of 90 gr.

The measure of an Angle is the Ark of the Circle described out of the angular point, intercepted between the Sides sufficiently produced.

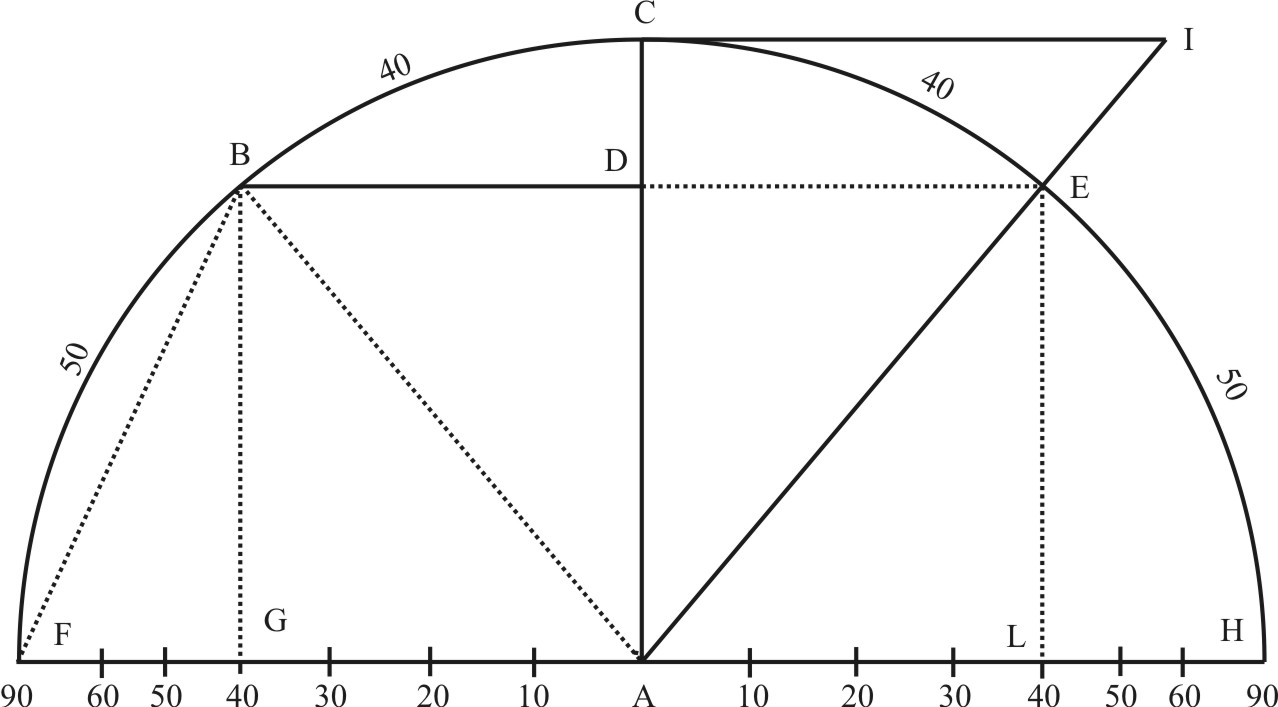
So the measure of a right Angle is always an Arc of 90 gr. and in this Example the measure of the Angle BAD in the following Figure, is the Ark BC of 40 gr. the measure of the Angle BAG, is the Ark BF of 50 gr.

The Complement of an Arc or of an Angle doth commonly signifie the Arc which the given Arc doth want of 90 gr. and so the Ark BF is the Complement of the Ark BC, and the Angle BAF, whose measure is BF, is the Complement of the Angle BAC; and on the contrary.

The Complement of an Ark or Angle in regard of the Semicircle, is that Ark which the given Ark wanted to make up 180 gr.: and so the Angle EAH is the Complement of the Angle EAF, as the Ark EH is the Complement of the Ark FE, in which the Ark CE is the excess above the Quadrant.

The Proportions which these Arks (being the measure of Angles) have to the Sides of a Triangle, cannot be certain, unless that which is crocked be brought to a straight Line, and that may be done by application of Chords, Right Sines, Versed Sines, Tangents and Secants to the Semidiameter of a Circle.

A Cord is a right Line subtending an Ark: so BE is a Chord of the Ark BCE, and BF a Chord of the Ark B40F.

A right Sine is half the Chord of the double Ark, viz. the right Line which falleth perpendicular from the one Extreme of the given Ark, upon the Diameter drawn to the other Extreme of the said Ark.

So if the given Ark be BC, or the given Angle be BAC, let the Diameter be drawn through the Center A unto C, and a Perpendicular BD be let down from the Extreme B upon AC, this Perpendicular BD shall be the right Sine both of the Ark BC, and also of the Angle BAC: and it is also the half of the Chord BE, subtending the Ark BCE, which is double to the given Ark BC. In like manner, the Semidiameter FA, is the right Sine of the Ark FC, and of the right Angle FAC; for it falleth perpendicular upon AC, and it is the half of the Chord FH.

This whole Sine of 90 gr. is hereafter called Radius, but the other Sines take their Denomination from the Degrees and Minutes of their Arks.

Sinu versus, the Versed Sine is a Segments of the Diameter, intercepted between the right Sine of the same Ark, and the Circumference of the Circle. So DC is the versed Sine of the Ark CB, and GF the Versed Sine of the Ark BF, and GH the Versed Sine of the Ark BH.

A Tangent is a right Line perpendicular to the Diameter drawn by the one extreme of the given Ark, and terminated by the secant drawn from the Center, through the other Extreme of the said Ark.

So the given Ark be CE, or the given Angle be CAE, let the Diameter be drawn through the Center A to C, and in C to Ac, be raised a Perpendicular CI. Then let another Lione be draqwn from the center A through E, till it meet with the Perpendicular CI in I; the Line CI is a Tangent, and AI is the Secant both of the Ark CE, and of the Angle CAE.