The Second Book of the Sector
CHAP. III.
Of the projection of the Sphere in Plano.
SECT. I.
To Project the Sphere in Plano, by streight Lines.
The Sphere may be projected in Plano in streight Lines, as in the Analemma, if the Semidiameter of the Circles given be divided in such sort as the Line of Sines on the Sector.
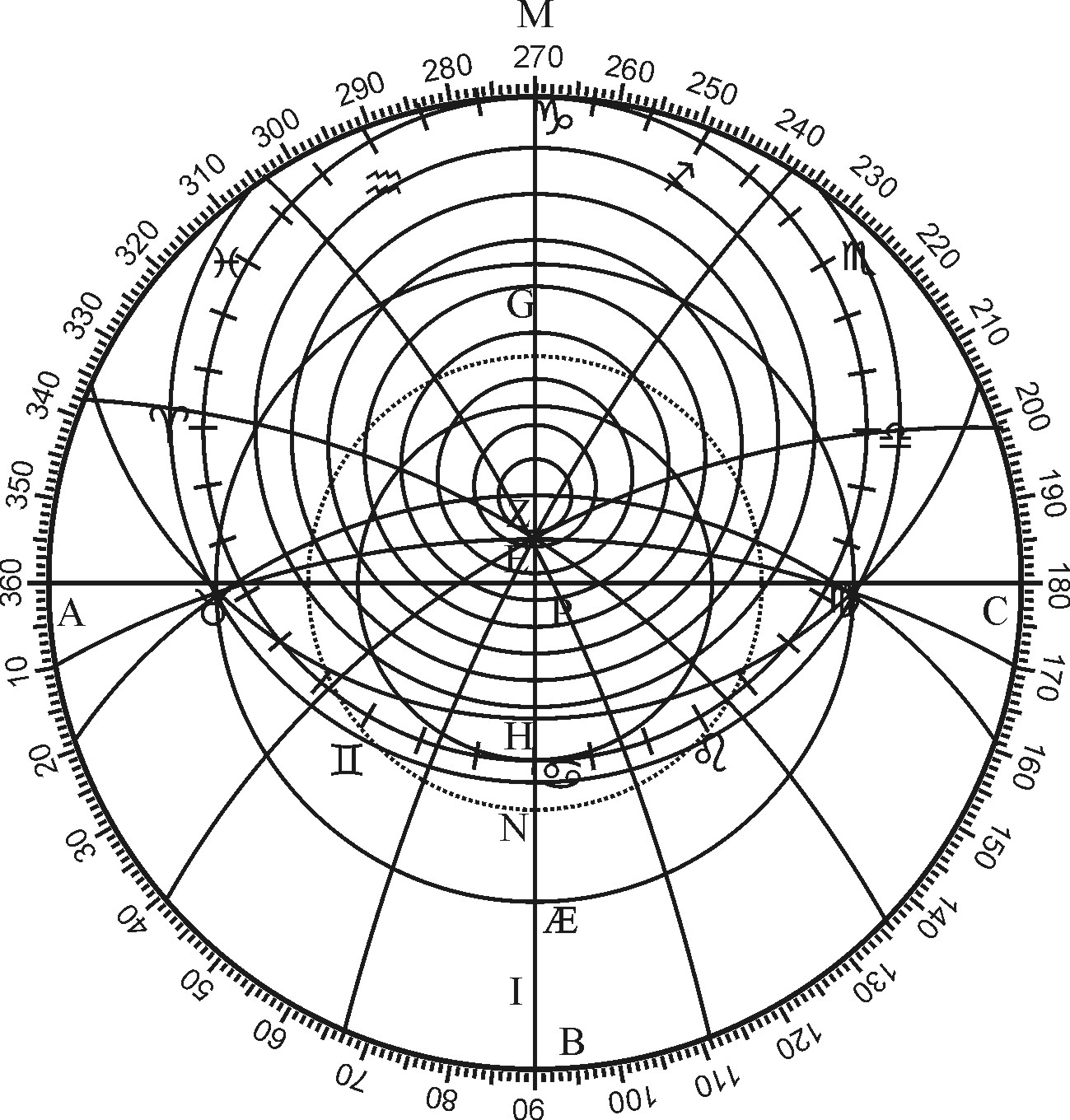
As if the Radius of the Circle given were Æ, the Circle thereon described may represent the Plane of the general Meridian, which divided into four equal parts in E, P, Æ, S, and crossed at right Angles with E Æ and PS; the Diameter E Æ, shall represent the Equator, and PS, the Circle of the hour of 6. And it is also the Axis of the World, wherin P stands for the North Pole, and S for the South Pole. Then may each quarter of the Meridian be divided into 90 degrees from the Equator towards the Poles. In which we number 23 degrees, 30 min. the greatest declination of the Sun from E to Northwards, from Æ to Southwards, the Line drawn from S to ♋ shall be the Ecliptick, and the Lines drawn parallel to the Equator through S and ♑ shall be the Tropick.
Having these common Sections with the Plane of the Meridian, if we shall divide each Semidiameter of the Ecliptick into 90 degrees, in such sort as the Sines are divided on the Sector. The first 30 degr. From A towards ♋ shall stand for the Sign of ♈. The 30 degr. next following for ♉. The rest of ♊, ♋, ♌, &c. in their order. So that by these means we have the place of the Sun for all times of the year.
If again we divide AP, AS, in the like sort, and set thereto the Numbers 10, 20, 30 &c. unto 90 degrees, the Lines drawn through each of these degrees parallel to the Equator shall shew the declination of the Sun, and represent the parallels of Latitude.
If farther, we divide AE, AÆ, and each of his Parallels equally in the like sort, and then carefully draw a Line through each 15 deg. so as it makes no Angles, the Lines so drawn shall be Elliptical, and represent the Hour-circles. The Meridian PES, the hour of 12 as noon; that next unto it drawn through 75 degrees from the Center, the hours of 11 and 1, that which is drawn through 60 degrees from the Center, the hours of 10 and 2, &c
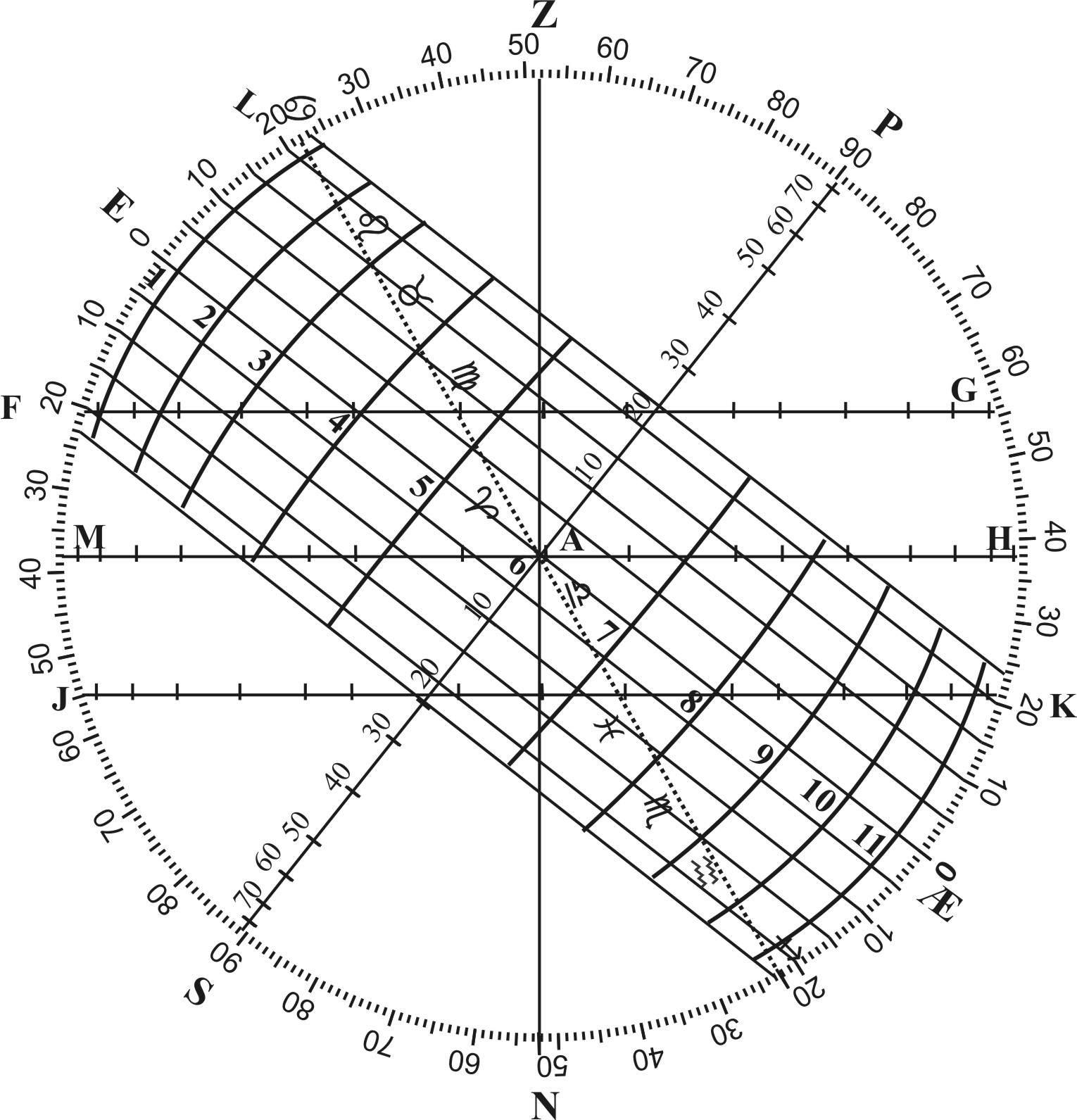
To these we may add the months of the year, and the days of each month, placing January about F, March about E, June about J, July about K, September about EÆ, December about the Tropick of ♋: and so the rest according to their Declination from the Equator.
Then having respect unto the Latitude, we may number it from E Northward unto Z, and there place the Zenith: by which, and the Center, the Line drawn ZAN. Shall the Vertical Circle, passing through the Zenith and Nadir, and through the Center at A, in the Points of East and West, and the Line MAH crossing it at right Angles, shall represent the Horizon.
These two being divided in the same sort as the Ecliptick and the Equator, the Line drawn through each degree of the Semidiameter AZ, parallel to the Horizon, shall be the Circles of Altitude, and the Division in the Horizon and his parallels shall give the Azimuth.
Lastly, if through 18 gr. In AN, be draw a right Line IK parallel to the Horizon, it shall shew the time when day breaketh, and the end of the twilight.
Some Uses of this projection.
For example of this Projection, let the place of the Sun be the last degree of ♉, the Parallel passing through this place is LD, and therefore the Meridian Altitude ML, and the depression below the Horizon at midnight HD: the Semidiurnal Ark LC, the Seminocturnal Ark CD; the Declination AB, the Ascensional difference BC, the Amplitude of Ascension AC. The difference between the end of twilight and the day break is very small; for it seems the Parallel of the Sun doth hardly cross the Line of twilight.
If the Altitude of the Sun be given, let a Line be drawn from it Parallel to the Horizon: so it shall cross the parallel of the Sun, and there shew both the Azimuth and the Hour of the day. As if the place of the Sun be given as before, the Altitude in the morning were found to be 20 degrees, the Line FG drawn Parallel to the Horizon through 20 degrees in AZ, would cross the parallel of the Sun in ☉. Wherefore F☉ sheweth the Azimuth, and L☉ the quantity of Hours from the Meridian. It seems to be about half an hour past 6 in the morning, and yet more than half a Point short of the East.
The distance of two places may be also shewed by this Projection, their latitudes being known, and their difference of Longitude.
For suppose a place in the East of Arabia, having 20 degrees of North Latitude, whose difference of Longitude from London, is found by an Eclipse to be 5 Hours 1/2. Let Z be the Zenith of London, the Parallel of Latitude for that other place must be LD, in which the difference of Longitude is L☉. Wherefore ☉ representing the site of that place, I draw through ☉ a parallel to the Horizon MH, crossing the Vertical AZ near about 70 degrees from the Zenith, which multiplied by 20 sheweth the distance of London, and that place to be 1400 Leagues. Or multiplied by 60, to be 4200 miles.
SECT. II.
To project the Sphere in Plano, by Circular Lines.
The Sphere may be projected in Plano by Circular Lines, as in the general Astrolabe of Gemma Frisius, by the help of the Tangent on the side of the Sector.
For let the Circle given represent the Plane of the general Meridian as before; let it be divided into four parts, and crossed at right Angles with E Æ the Equator, and PS the Circle of the Hour of 6, wherein P stands for the North Pole, and S for the South Pole: Let each quarter of the meridian be divided into 90 degrees, and so the whole into 360, beginning from P, and setting to the Number of 10, 20, 30, &c. 90 at Æ, 180 at S, 270 at E, 360 at P. The Semidiameters AP, AÆ, AS, Æ, may be divided according to the Tangents of half their Arks, that is a Tangent of 45 degrees, which is always 10000, equal to the Radius, shall give the Semidiameter of 90 degrees, a Tangent of 40 degrees 83910, shall give 80 degrees in the Semidiameter: a Tangent of 35 degrees 70021 shall give 70, &c. So that the Semidiameter may be divided in such sort as the Tangent on the side of the Sector, the difference being only in their denomination.
Having divided the Circumference and the Semidiameters, we may easily draw the Meridians and the Parallels by the help of the Sector.
The Meridians are to be drawn through both the Poles P and S, and the degrees before graduated in the Equator. The distance of the Center of each Meridian from A, the Center of the Plane, is equal to the Tangent of the same Meridian, reckoned from the general Meridian PÆSE, and the Semidiameter equal to the Secant of the same degree.
As for example, If I should draw the Meridian PBS, which is the tenth from PAES, the Tangent of 10 gr. 17633, giveth me AC, and the Secant of 10 gr. 101543, giveth me SC, wherefore C is the Center of the Meridian, PBS and CS his Semidiameter: so AF: Tangent of 20 gr. 36397 sheweth F to be the Center of PDS, the twentieth Meridian from PÆS, and AG the Tangent of 23 gr. 30 m. 43481, sheweth G to be the Center of P♋S, &c.
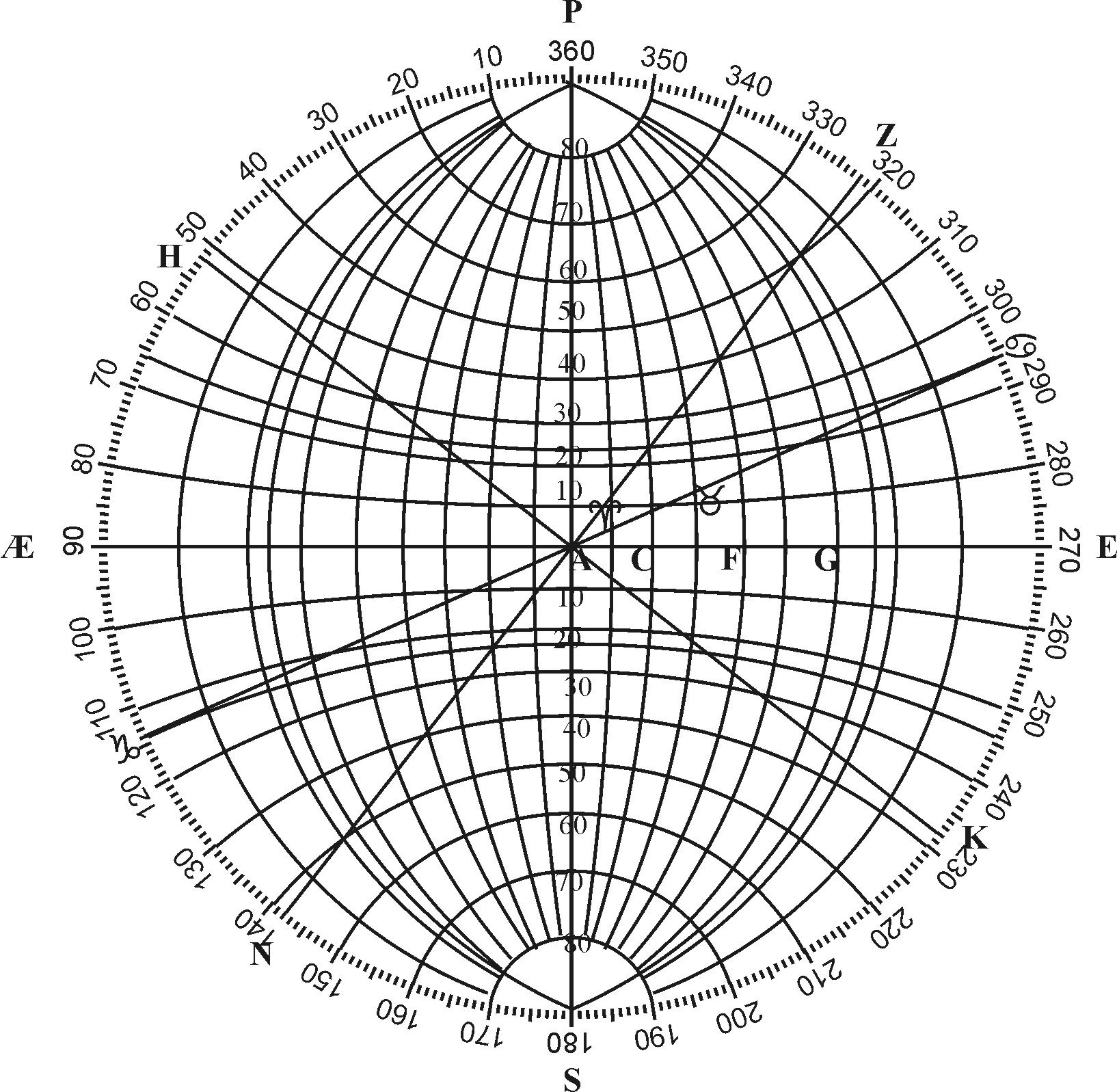
The Parallels are to be drawn through the degrees, in AP, AS, and their correspondent degrees in the general Meridian. The distance of the Center of each parallel from A the Center of the Plane, is equal to the Secant of the same Parallel from the Pole, and the Semidiameter equal to the Tangent of the same degree. As if I should draw the parallel of 80 degrees, which is the tenth from the Pole S, first I open the Compasses unto AC the Tangent of 10 degrees 17633, and this giveth me the Semidiameter of this Parallel, whose center is a little from S, in such distance as 101543 the Secants SC is longer than 10000, the Radius SA.
The Meridians and Parallels being drawn, if we number the 23 deg. 30 min. from E to ♋ Northward, from Æ to ♑ Southward, the Line drawn from ♋ to ♑ shall be the Ecliptick: which being divided in such sort as the Semidiameter AP, the first 30 degrees from A to ♋ shall stand for the Sine of ♈; the 30 degr. next following for ♉; the rest for ♊, ♋, ♌, &c. in their order.
If farther we have respect unto the latitude, we may number it from E Northward unto Z, and there place the zenith, by which and the Center, the Line drawn ZAN, shall represent the vertical Circles, and the Line MAH, crossing it at right Angles, shall represent the Horizon, and these divided in the same sort as AP, the Circles drawn through each degree of the Semidiameter AZ, Parallel to the Horizon, shall be the Circles of Altitude: and the Circles drawn through the Horizon and his Poles, shall give the Azimuths.
Some Uses of this Projection.
For Example of this Projection, let the place of the Sun be in the beginning of ♒, the Parallel passing through this place is ♒☉L, and therefore the Meridian Altitude ML, and the depression below the Horizon at Midnight H⚪, the semidiurnal Ark L☉, the Seminucturnal Ark ⚪☉, the Declination AR, the Ascensional difference R☉, the Amplitude of the Ascension A☉.
Or if A be put to represent the Pole of the World, then shall PÆSE stand for the Equator, and P♋S♑ for the Ecliptick, and the rest which before stood for Meridians, may now serve for particular Horizons, according to their several Elevations. Then suppose the place of the Sun given to be 24 degrees of ♉, his Longitude shall be PI, his right Ascension PH, his Declination HI. And if the place given be 19 degrees of ♑, his Longitude shall be PK, his right Ascension PN, his Declination NK. Again, the Declination brought to the Horizon of the place, shall there shew the Ascensional difference; Amplitude of Ascension, and the like conclusions of the Globe. But I intend not here to shew the Use of the Astrolabe, but the Use of the Sector in Projection.
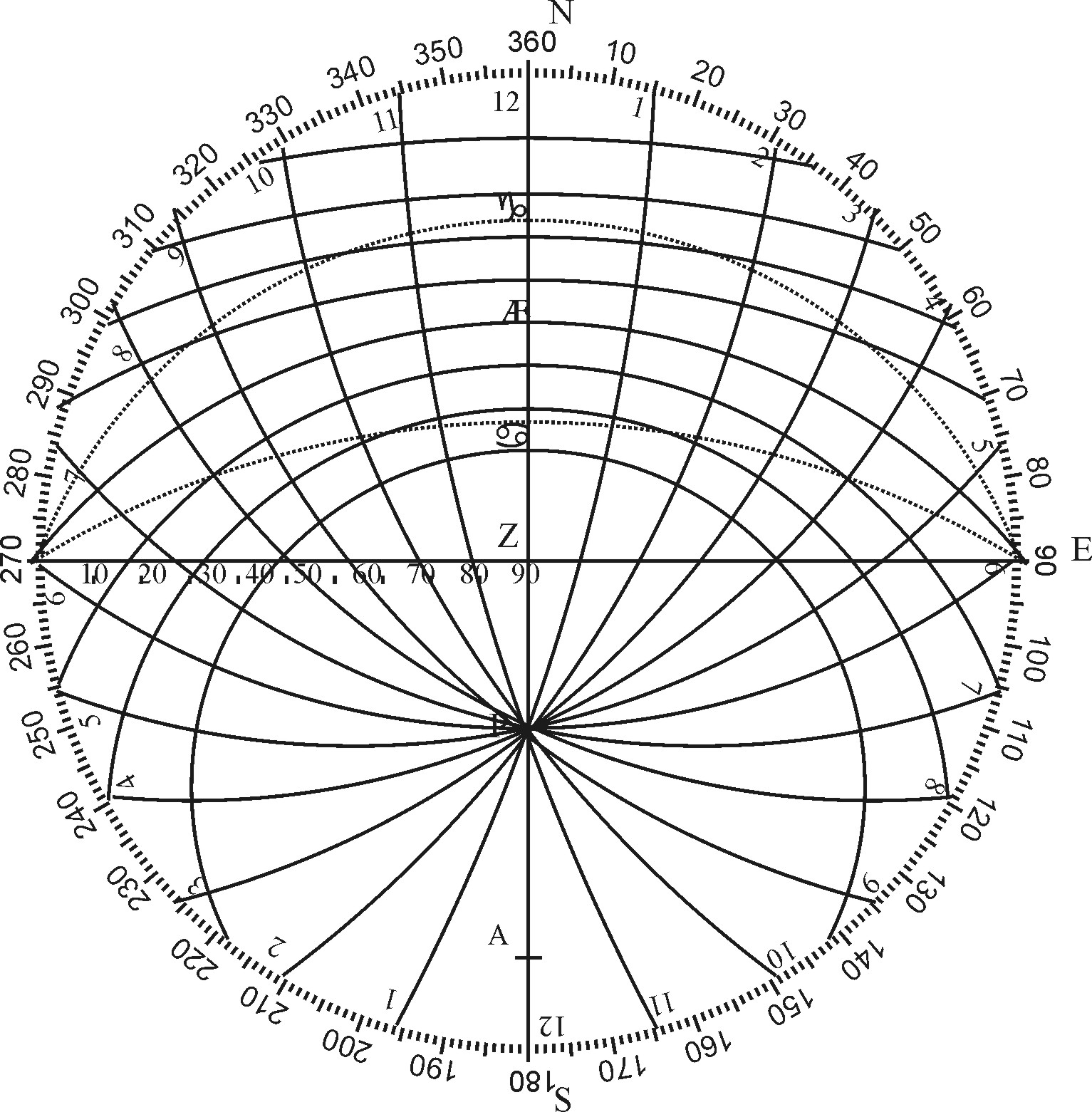
And after this manner may the Nocturnal be projected to shew the Hour of the Night, whereof I will set down a Type for the use of Seamen.
It consists, as you see, of two parts, the one is a Plane divided equally according to the 24 hours of the day, and each hour into quarters or minutes, as the Plane will bear: the Line from the Center to XII, stands for the Meridian, and XII stands for the hour of 12 as midnight. The other part is a rundle for such stars as are near the North-pole, together with the twelve months, and the days of each month fitted to the right Ascension of the stars. Those that have occasion to see the South-pole, may do the like for the Southern Constellations, and put them in a Rundle on the back of this Plane, and so it may serve for all the World.
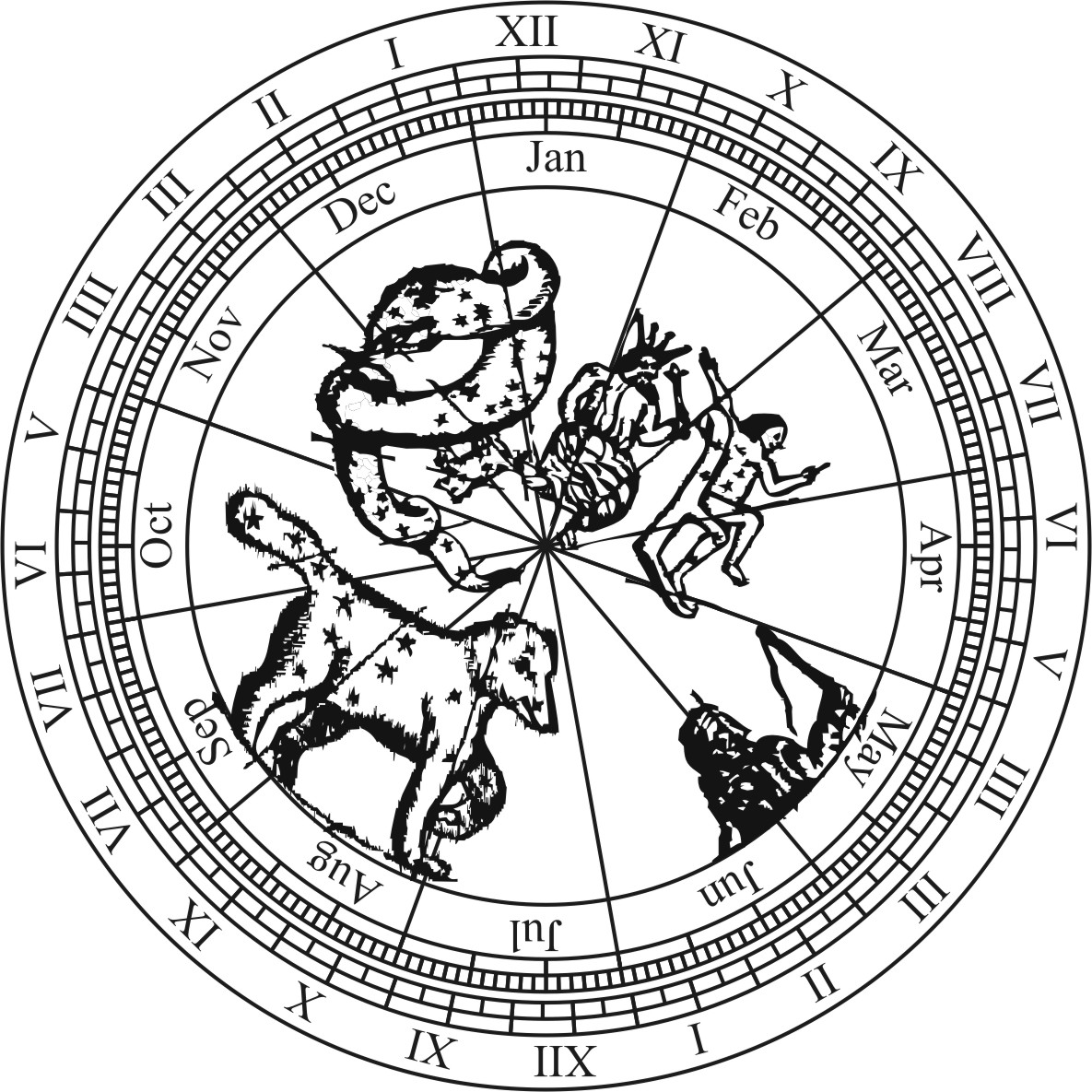
The Use of this Nocturnal.
The Use of this Nocturnal is easie and ready. For look up to the Pole, and see what Stars are near the Meridian: then place the Rundle to the like situation, so the day of the months will shew the hour of the Night.
SECT III.
Another way to Project the Sphere by Circular Lines.
The Sphere may be projected in Plano, by circular Lines, as in the particular Astrolabe of John Stophlerin (Anm.: Stofflerinus (lat), eigentlich Johann Stöffler, 1452 - 1531), by help of the Tangent, as before. (Anm. gemeint ist: Johannes Stöffler, Elucidatio Ususque Fabricae Astrolabii (Abhandlung über den Gebrauch und die Herstellung des Astrolabs), (Erstausgabe 1512) Paris, Marnef & Cavellat, 1585)
For let the Circle given represent the Tropick of ♑, let it be divided into four parts, and crossed at right Angles with AC the Equinoctial Colure, and MB the Solstitial Colure, and general Meridian, the Center P representing the Pole of the World. Let each quarter be divided into 90 degrees, and so the whole into 360, beginning from A towards B. The Meridian PM or PB, may be divided according to the Tangent of half his Ark. So as the Ark from the North Pole to the Tropick ♑ being 90 degrees, and 23 degrees 30 min. that is 113 degrees 30 min. and the half Ark 56 degrees 45 min. the Meridian shall be divided into 90 degrees and 23 degrees 30 min. in such sort as the Tangent of 56 degrees 45 min. on the side of the Sector is divided into degrees and half degrees., of which PÆ the Ark of the Equator 90 degrees from the Pole, shall be given by the Tangent of 45 degrees. And P♋ the Ark of the Summer Tropick 66 degrees 30 min, from the Pole, shall be given by the Tangent of 33 degrees 15 min. And the Circles drawn upon the Center P through Æ and ♋, shall be the Equator, and the Summer Tropick.
Having Equator and both Tropicks, the Ecliptick ♈ ♋ ♎ ♌ shall be drawn from one Tropick to the other, through the intersection of the Equator and the Equinoctial Colure. And it may be divided first into twelve Signs after thi manner: PE the Ark of the Pole of the Ecliptick 23 degrees 30 min. from the Pole of the World, shall be given by the Tangent of 11 degrees 45 min. The Center of the Circle of Longitude passing through this Pole E♈ and ♎ shall be found at D (somewhat below B) by the Tangent of 66 degrees 30 min. Then through D draw aa occulte Line parallel to AC, and divide it on each side from D, in such sort as the Tangent is divided on the side of the Sector, allowing 45 degrees to be equal to DE, so the thirtieth degree from D toward the right hand, shall be the Center of the Circle of Longitude passing through E♉ and ♍. The sixtieth degree, the Center of ♊E♐. The thirtieth gr. from D towards the left hand, the center of ♓E♏. The sixthieth, the Center of ♈E♌. And the other intermediate degrees shall be the Centers to divide each sign into 30 gr.
If farther we have respect unto the latitude, we may (the Meridian being before divided) number it fom P Northward unto H, and there place the North Intersection of the Meridian and Horizon: then the Complement of the latitude being numbered from P Southward unto Z, shall there ive the zenith; and 90 degr. from Z Southward unto F, shall there give the South intersection of the Meridian and Horizon. The middle between F and H shall be G the Center of the Horizon ♈H♎F, passing through the beginning of ♈ and ♎, unless there be some former errour.
All parallels to the Horizon may be found in like sort by their Intersections with the Meridian, and the middle between those Intersections is always the Center.
The Azimuths may be drawn as the Circles of Longitude were before. For the Circle of the first Verticle ♈Z♎, will be found at I (somewhat near unto B) by the tangent of the latitude. And if through I we draw an occult Line parallel to AC, and divide it on each side from I, in such sort as the tangent is divided on the side of the Sector, allowing 45 degrees to be equal to IZ, these Divisions unto Z, shall be the Semidiameter whereon to describe the rest of the Azimuths.
Some Uses of this Projection.
For example of this Projection, let ☉ the place of the Sun given be 10 degr. of ♉: a right Line drawn from P through this place unto the Equator, shall there shew his right Ascension ♈K, and his Declination K☉. Then may we on the Center P and Semidiameter ☉P draw an occult Parallel of Declination, crossing the Horizon in L, M. the Meridian in G and N. So the right Lines PL and PM produced, shall shew the time of the Suns rising and setting, ♈Q the difference of Ascension, R the difference of Descension, ♈L the Amplitude of rising, and ♎M the Amplitude of his setting, LNM sheweth the length of the night, ZG sheweth his distance from the Zenith at noon, HN his depression below the Horizon at midnight. And then having the Altitude of the Sun at any one time of the day, the Intersection of the parallel of Altitude with the parallel of Declination, sheweth the Azimuth, and a right Line drawn from P through this Intersection, giveth the hour of the day.
SECT. IV.
A third way to Project the Sphere in Plano, by Circular Lines.
The Sphere may be Projected in Plano by Circular Lines, after the manner of the old concave Hemisphere, by the help of the tangent on the side of the sector.
For let the Circle given represent the Plane of the Horizon, let it be divided into four parts, and crossed at right Angles with SN the Meridian, and EV the Verticle; so as S may stand for the South, N for the North, E for the East, W for the West part of the Horizon, and the Center Z represent also the Zenith. Let each quarter of the Horizon be divided into 90 degrees, and so the whole into 360 degrees, beginning from N and setting to the numbers 10, 20, 30, &c. 90 at E, 180 at S, 270 at W, 360 at N.
The Semidiameters ZN, ZS, may be divided according to the Tangent of half their Arks: so as the Ark from the Zenith to the Horizon being 90 gr. and half the Ark 45 gr. as was shewed before in the second Projection. And if from Z we draw Circles through each of these Divisions, they shall be parallel of Altitude.
Then having respect unto the Altitude, we may (the Meridian being before divided) number it from Z to Æ, and there place the Intersections of the Meridian and Equator. The Complement of the latitude from Z unto P shall there give the Pole of the World, and 90 further from P, shall there give the other intersection of the Meridian and Equator.
The middle between these intersections shall be A the Center of the Equator, passing through E and W, unless there be some former error. The Intersections of the Tropicks depend on the Equator. From Æ 23 degrees 30 min. farther shall be ♑ the intersection of the Meridian and the Southern Tropick. From Æ 23 degrees 30 min. nearer shall be ♋, the Intersection of the Meridian and the Northern Tropick. The Intersections of the other intermediate Parallels shall be given in like sort, by their degree of distance from the Equator, and the middle between those Intersections is always the Center.
The Hour Circles may be here drawn as the Azimuths in the third Projection. For the Center EPW, the hour of 6, will be found at B (somewhat near unto N) by the Tangent of the latitude. And if through B we draw an occult Line parallel unto EW, and divide it on each side from B, in such sort as the Tangent is divided on the side of the Sector, allowing 45 degrees to be equal to BP, and 15 degrees, for every hour, those Divisions shall be the Centers, and the distance from the Division unto P, shall be the Seimidiameters, whereon to describe the rest of the hour Circles.
The Ecliptick may be drawn as the Equator. For the Center of that half which hath Southern Declination, shall be given by the Tangent of the Altitude, which the Sun hath in his entrance into ♑. And the center of the other half by the Tangent of his Altitude, at his entrance into ♋, and it may be divided, as in the former Projection, or else by the Tables calculated to that purpose.
To these Circles thus drawn, if we shall add the months of the year, and the days of each month, as we may well do, at the Horizon, on either side, between the Tropicks: this Projection shall be fitted for the most useful Conclusion of the Globe, as by examples following may appear.
Some Uses of this Projection.
For the day of the month being given, the parallel that shooteth on it, doth shew what declination the Sun hath at that time of the year. And where this Parallel crosseth the Ecliptick, there is the place of the Sun. Or the place of the Sun being first given, the Parallel which crosseth it, shall at the Horizon shew that day of the month. Either of these then being given, or only the parallel of Declination, we may follow it, first unto the Horizon, there the distance of the end of the parallel from E or W, sheweth the Amplitude; the same among the hour-circle sheweth the time when the Sund riseth or setteth. Then having the Altitude of the Sun at any time of the day, the Intersection of the Parallel of Declination with the Parallel of Altitude sheweth the hour of the day; and a right Line drawn form Z, through this Intersection to the Horizon, giveth the Azimuth.
Thus in either of these Projections, that which is otherwise most troublesome, is easily done by help of the Tangent Line, and what I have said of this Line, the same may be wrought by Scale and Numbers of the Table of Tangents.
| ☞ | Note, that if unto any of these three last Projections, there be added an Index equal to the Semidiameter of the Circle, to move upon the Center of the Projection, and the fiducial edge thereof divided according to the Tangents of half Arks, the Semidiameters need not be divided, and the Instruments will then be fitly accommodated to perform many Conclusions of the Sphere. | |
| By the former way of Projecting of the Sphere, the whole Ark of Dialling may be performed upon any of them, but especially upon this last, which may be fitted to the Horizon of any place, the manner whereof in this place I shall briefly deliver. | ☜ |
- For an Horizontal Dial.
If straight Lines be drawn from the Center of the Projection through the Intersections of the hour Circles with the outermost Circle or Horizon, those Lines so drawn shall be the true hour Lines of an Horizontal Dial in that Latitude for which the Projection was made, for the hour Circles cut the Horizon at those degrees of distance. - For an Erect direct North or South Dial.
If an Index be divided as the Semidiameter of the Projection ZW is, on both sides, and laid upon the same Diameter WE, the hour Lines of the Projection will cut the same Index in such degrees from the Meridian on either side, as the hour Lines on such a North or South Dial ought to have upon the Plane: As:degr. min. 11 1 9 28 10 2 19 54 The hour Lines of 9 and 3 do cut the Index at 31 54 from the Meridian. 8 4 47 09 7 5 66 42
And these are the true hour distances for a North or South Plane in this Latitude of 51 degrees 30 min. for which this Projection was made. - For a Vertical Declining Dial.
Suppose an upright Plane to decline from the South Westward 24 degr. 20 min. Such aPlane is described in the third Book of this Treatise Chap. 7. If you lay your Index to 24 degr. 20 min conted from E towards S, and there keep it fixed, the hour Lines of the Projection will cut the Index in these degrees from the Meridian, on either side thereof, at which they are to be drawn upon the Dial Plane. - For direct Incliners.
Let the Inclining Plane be projected upon the Scheme, a Ruler laid to the Pole of the inclining Plane, and to the several Points where the hours cross the Plane, the Ruler will cut the outermost Circle in the degrees the hour Lines ought to have upon such an inclining Plane.
Thus let the Circle WÆE, which is the Equinoctial Circle, represent a Plane inclining to the Horizon, a Ruler laid to the Pole of the World (which is the Pole of the Equinoctial Circle) and the several intersections of the hour Circles with this Circle, shall cut the outermost Circle in every fifteenth degree, and such distance ought each hour have from other upon the Plane. - For Declining inclining Planes.
Let a Plane decline from the South Westward 24 degrees 20 min. and incline to the Horizon Northward 36 degrees, such a Plane is represented in the Diagramm of the seventh Chapter of the third Book of this Teatise, by the Circle BMD. Now a Ruler laid upon the Pole of this Plane, (which is the Line QH, 90 degrees distant from M) and the intersections of the hour Circles with the Plane, shall cut the respective hour Lines of such a declining inclining Plane ought to have upon the Dial Plane.
SECT. 5.
Of Projecting of the Sphere upon Oblique Circles.
In the four first Sections of this Chapter, Mr. Gunter hath shewed how to Project the Sphere in Plano upon the principal Great Circles of the Sphere, viz. Twice upon the Plane of the Meridian, once upon the Tropick of ♑, or the Equinoctial, (parallel thereto) and lastly upon the Horizon.
To these Projections I think it will not be impertinent (but very beneficial and satisfactory to the Reader) to shew how the Sphere may be Projected in Plano upon any Oblique Circle, as upon any Plane whatsoever and howsoever situate, for all or most Dial Planes are Oblique Circles, and are Horizons in some part of the World or other. As for Example, A Dial Plane declining from South Westward 24 degrees 20 min and inclining Northward 36 degrees (such is the Dial Plane in the tenth Chapter of the third Book of this Treatise of Dialling) will in some place or other be an Horizontal Plane. And by projecting of the Circles of the Sphere in their true positions upon this Oblique Plane, you shall not only discover in what Longitude and Latitude this will be an Horizon, but will also delineate out unto you tha places of the Hour-lines proper for this declining inclining Plane, in a quite different manner and form than that which Mr. Gunter hath shewed how to make a Diall in the forementioned tenth Chapter of the third Book, by drawing the Plane upon the Horizontal Projection for this Latitude. And seeing the difference of the two ways of working are so various, and the variety that will appear in the placing of the Circles of the Shere in their true positions upon such an Oblique Plane cannot but be both beneficial and delightful, I shall here insert the manner how the same may be effected, not only upon this, but upon any other Oblique Plane whatsoever.
To proceed then, Let the Circle HXOD, represent a Dial Plane declining from South Westward 24 degrees 20 min. and inclining Northward 36 degrees.
- Draw the Diameter HO, and cross it at right Angles with the Line CF meeting in the Center Q.
- Take the half Tangent of 36 degrees, the Planes inclination, and set it from Q to Z, so shall Z be the Zenith of the Place.
- Take the half Tangent of 54 degrees, the Complement of the Planes inclination, and set that from Q to B, so shall B be the Point through which the Horizon of the plave must pass.
- Take the Tangent of 36 degrees the Planes Inclination, and set it from Q to C. Or take the Secant of 36 degrees, and set it from B to C, so shall C be the Centrer of the Horizon HBO.
- Take the Tangent of 54 degrees, the Complement of the Inclination, and set it from Q to F.
- Take 24 degrees 20 min out of your Line of Chords and set that distance from H to C, from D to C, and from O to C.
- A Ruler laid from Z to C, D, and C, will give the Points W, S and E, for the West South and East Points thereof.
- Draw FG perpendicular to QF, or parallel to HO, and extend it as far as you shall see requisite.
- Draw a Line through the Points E and W extending it till it cross the Line FG last drawn, at G, so shall G be the Center of the Meridian of the place represented by PZS.
- Lay a Ruler from W to Z and it will cut the Circle in a, from which Point a let 38 degrees 30 min the Co-latitude to b, and a Ruler laid from W to b will give the Point P in the Meridian for the Pole of the World.
- Set 90 degrees of your Chords from b to f, and from f to g. A Ruler laid from W to f gives Æ in the Meridian Circle, for the Equinoctial Point, and from W to g gives M for the South Pole, and a right Line drawn through PQ and M shall be the Axis of the World.
- Through the Points WÆE draw the Equinoctial Circle, to find the Center whereof.
- Divide WE into two equal parts in R, and raise the perpendicular RT, drawing it forth till it meet with QP being extended, here represented by the two Lines RT and QV, whose meeting shall be the Center of the Equinoctial, which QT extended would be equal to the Secant of the height of the Pole above the Plane. Or if from T you draw a Line through C it will intersect QV in the Center of the Equinoctial also.
- Divide MP in two equa parts in D, and draw DG at right Angles to PM, and extend DG infinitely.
- Upon P, at the distance PD (or any other) describe the Semicircle LD, and laying a Ruler from P to G the Center of the Meridian, it will cut the Semicircle LDN in L, at which Point L begin to divide LDN into twelve equal parts, and a Ruler laid from P through each of those equal parts shall give the Tangents of 15, 30, 45, &c upon the Tangent GD and shall be the Center of the several Meridians, G being the Center of twelve a clock, or the Meridian of the Place.
- 16. From the Center Q through the Points where the several Meridians do cut the Primitive Circle draw right Lines, and those Lines shall be the true hour Lines of a South Palne declining Westward 24 degrees 20 min. and inclining Northward 36 degrees in the latitude of 51 degrees 30 min.
And from this Scheme may further be found that,
| degr. | min. | |
| 1. The Elevation of the Meridian HA is | 69 | 54 |
| 2. The difference of the Meridians QP and Æ is | 14 | 41 |
| 3. The height of the Stile PA is | 17 | 26 |
| 4. The distance of the Substile and Meridian AX is | 04 | 30 |
Note, In like manner might be inserted in this Projection, the Tropicks and other Parallels of the Suns place or Declination; The Azimuths, Almicanthars, the Ecliptick, and other (either small or great) Circles; as is instanced in the Scheme by the Tropick of Cancer, which is thereon described; but of this Oblique Projection I have said enough in this place.