Kursbestimmungen
Wenn man bei einem Törn weiss, wohin man will, bestimmt man zunächst den Kurs, mit dem man lossegeln will. Dabei unterscheidet man drei Berechnungsmethoden, die man je nach Entfernung vom Start- zum Zielort anwendet. Als nächstes interessiert bei der Törnplanung die Entfernung zwischen den beiden Orten. Die kann man aber in keinem der hier dargestellten Fälle aus der Karte ablesen: man muss immer rechnen.
- Für kurze Entfernungen, d. h. wenn man die Erdoberfläche als eben annehmen kann, verwendet man die Methode der mittleren Breite. Diese Berechnung entspricht dem Ablesen des Winkels zwischen der Nordrichtung und der Verbindungslinie der beiden Orte auf der Seekarte. Die Mercator-Projektion ist ja winkelgetreu, aber nicht flächengetreu (damit kann man den Kurs, aber nicht die Entfernung direkt aus der Karte entnehmen).
- Ist die Entfernung zu groß und muss man die Kugelgestalt der Erde berücksichtigen, rechnet man nach der Methode der Loxodrome. Die wird man anwenden, wenn Start- und Zielort nicht auf der gleichen Karte eingezeichnet sind.
- Schließlich für sehr weite Entfernungen — wenn man über mehrere Zeitzonen den kürzesten Weg sucht — verwendet man die Methode der Orthodrome.
- Einfluß der Strömung,
- Einfluß der Bewegung des Ziels (Treffpunktproblem),
- Besteckversetzung,
- Einfluß des Windes.
Aus den Ortskoordinaten nach der Methode der mittleren Breite
Für unsere Betrachtungen ist die Erde eine Kugel (was ja exakt nicht stimmt: sie ist kartoffelförmig). Wenn die Entfernungen nicht allzu groß sind, kann man die Erdoberfläche aber als eben betrachten, ohne einen zu großen Fehler zu machen; das Rechnen wird dann einfacher. In der Praxis nimmt man die einfachere Methode der mittleren Breite bis zu einer Entfernung von etwa 100 sm (andere Quellen sagen bis 10°, also 600 sm), darüber die Methode der der gemittelten Breite (Loxodrome), die von einer Kugelgestalt der Erde ausgeht. Nun sei nicht verschwiegen, dass die mit einer der beiden genannten Methoden ermittelte Entfernung nicht notwendigerweise die kürzeste ist. Auf der Kugel liegt die kürzeste Entfernung zwischen zwei Orten auf einem Großkreis, so dass man als dritte Berechnungsart noch die Großkreisnavigation (Orthodrome, nach den Regeln der sphärischen Trigonometrie) kennen sollte, wenn man nicht auf oder dicht an einem Meridian — also nach Norden oder Süden — segelt.
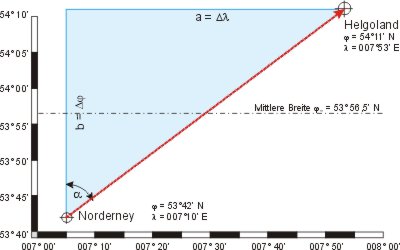
Für eine Fahrt von Norderney (53° 42′ N, 007° 10′ E) nach Helgoland (54° 11′ N, 007° 53′ E) kann man die Erde als eben ansehen. Es ergibt sich das linke Bild in rechtwinkligen Kartenkoordinaten.
Das blaue, rechtwinklige Dreieck hat die Katheten a Längendifferenz und b Breitendifferenz. Die Hypotenuse ist die Entfernung, der Winkel α der Kartenkurswinkel.
Wegen der Verzerrung der Mercatorprojektion entspricht die Bodenminute (ein 21.600stel des Erdumfangs) nur auf einem Meridian oder dem Äquator einer Seemeile. Die Breitenkreise sind Kleinkreise und haben einen geringeren Umfang, deshalb ist die Bogenminute dort kürzer und gehorcht der Beziehung Δx = Δλ·cos φ, wobei φ die geographische Breite ist. (Ableitung des Zusammenhanges siehe unter Sphärische Trigonometrie.) Zur Vereinfachung setzt man zur Entfernungsberechnung die mittlere Breite φm ein, die das arithmetische Mittel der beiden Ortsbreiten von Anfangs- und Endhafen der Reise ist (φm = (53° 42′ + 54° 11′) ⁄ 2 = 53° 56,5′ = 53,94°).
- a = Δλ′ = Δλ · cos φm = 43′ · cos (53,94°) = 25′, (Δλ in Bogenminuten oder sm),
- b = Δφ = 29′ (in Bogenminuten oder sm).
Der Winkel α des Dreiecks ergibt sich aus der Definition des Tangens: tan α = Gegenkathete ⁄ Ankathete.
- tan α = (Δλ · cos φm) ⁄ Δφ = a ⁄ b = 25′ ⁄ 29′ = 0,862 ⇒ α = 41,6°.
Die Länge c der Hypotenuse (Abstand der Orte) erhält man aus der Definition des Sinus als
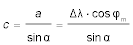 .
.
Beispielrechnung
Mit dem Rechenschieber führt man die Berechnung in zwei Schritten aus.
- Läufer über φm auf Skala S, 1 (oder 10) auf C unter Läuferstrich, Läufer auf Δλ verschieben (Ergebnis 1 merken); wenn Δλ′ kleiner als Δφ, auf Skala C unter den Läuferstrich (über das Ergebnis der Multiplikation) Läufer auf das Ergebnis der Division (1 oder 10 auf C) und auf T den Winkel ablesen. IstΔλ′ kleiner als Δφ, so liest man auf T den Cotangens (von rechts) ab.
- Sinus des Winkels merken und Läufer über Ergebnis 1 auf D einstellen und den gemerkten Sinuswert auf C unter den Läuferstrich stellen. Unter 1 (oder 10) auf C liest man auf D das Ergebnis ab. Da die Werte der Winkelfunktionen für Winkel < 90° immer kleiner als 1 sind, ist die Abschätzung der Kommastelle abhängig von Δλ in Bogenminuten.
Nun muss man nur noch aus dem Dreieckswinkel auf den Kartenkurs schließen.
Dabei muss man unterscheiden, ob die Längendifferenz der Ortskoordinaten größer ist als die Breitendifferenz, oder umgekehrt und ob man den Tangens oder den Cotangens abgelesen hat (wenn man die kleinere durch die größere Zahl teilt, erhält man mit dem Tangens den spitzesten Winkel!).
- a = Δλ < b = Δφ, Tangens ablesen,
- oder
- a = Δλ > b= Δφ, Cotangens ablesen.
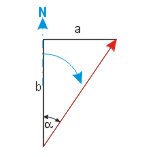
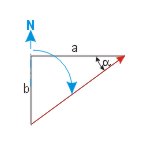
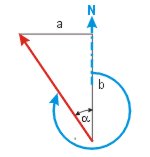
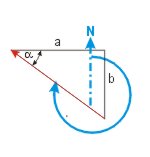
| Vom Dreieckswinkel zum rechtweisenden Kurs | |
|
|
| KaK = α | KaK = 90° - α |
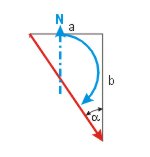
|
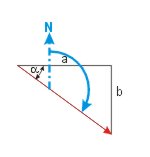
|
| KaK = 180° - α | KaK = 90° + α |
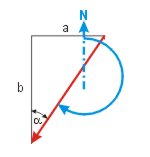
|
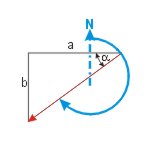
|
| KaK = 180°+ α | KaK = 270° - α |
|
|
| KaK = 360° - α | KaK = 270° + α |
|
|
|
|
|
© Rainer Stumpe URL: http://www.rainerstumpe.de |