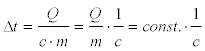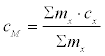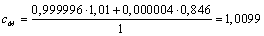The
American Journal
of
Science and Arts.
Vol. XXII. — November, 1856.
Circumstances affecting the Heat of the Sun's Rays;
by Eunice Foote..
(Read before the American Association, August 23rd, 1856.)
My investigations have had for their object to determine the different circumstances that affect the thermal action of the rays of light that proceed from the sun.
Several results have been obtained.
First. The action increases with the density of the air, and is diminished as it becomes more rarified.
The experiments were made with an air-pump and two cylindrical receivers of the same size about four inches in diameter and thirty in length. In each were place two thermometers, and the air was exhausted from one and condensed in the other. After both had acquired the same temperature they were placed in the sun, side by side, and while the action of the sun's rays rose to 110 °[F] in the condensed tube, it attained only 88 °[F] in the other. I had no mean at hand of measuring the degree of condensation or rarefaction.
The observations taken once in two or three minutes, were as follows:
| Exhausted Tube | Condensed Tube | ||
| In shade. | In sun. | In shade. | In sun. |
| 75 | 80 | 75 | 80 |
| 76 | 82 | 78 | 95 |
| 80 | 82 | 80 | 100 |
| 83 | 86 | 82 | 105 |
| 84 | 88 | 85 | 110 |
This circumstance must affect the power of he sun's ray in different places, and contribute to produce their feeble action on the summits of lofty mountains.
Secondly. The action of the sun's rays was found to be greater in moist than in dry air.
In one of the receivers the air was saturated with moisture--- in the other it was dried by the use of chlorid of calcium.
Both were placed in the sun as before and the was as follows:
| Dry Air. | Damp Air. | ||
| In shade. | In sun. | In shade. | In sun. |
| 75 | 75 | 75 | 75 |
| 78 | 88 | 78 | 90 |
| 82 | 102 | 82 | 106 |
| 82 | 104 | 82 | 110 |
| 82 | 105 | 82 | 114 |
| 88 | 108 | 92 | 120 |
The high temperature of moist air has frequently been observed. Who has not experienced the burning heat of the sun that precedes a Summer shower? The isothermal lines will, I think, be found to be much affected by the different degrees of moisture in different places.
Thirdly. The highest effect of the sun's rays have found to be in carbonic acid gas.
One of the receivers was filled with it, the other with common air and the result was as follows:
| In Common Air. | In Carbonic Acid Gas. | ||
| In shade. | In sun. | In shade. | In sun. |
| 80 | 90 | 80 | 90 |
| 81 | 94 | 84 | 100 |
| 80 | 99 | 84 | 110 |
| 81 | 100 | 85 | 120 |
The receiver containing the gas became itself much heated — very sensibly more than the other — and on being removed, it was many times as long in cooling.
An atmosphere of that gas would give to our earth a high temperature; and if as some suppose, at one period of its history the air had mixed with it a larger proportion than the present, an increased temperature from its own action as well as from increased weight mut have necessarily resulted.
On comparing the sun's heat in different gases, I found it to be in hydrogen gas 104 °[F]; in common air, 106 °[F]; in oxygen gas, 108 °[F]; and in carbonic acid, 125 °[F].
- Quelle:
- Eunice Foote: Circumstances affecting the Heat of the Sun's Rays. The American Journal of Science and Arts. Second Series, Volume 22, November 1856, pages 382-383.
Diese Beobachtung ist aus heutiger Sicht leicht mit der spezifischen Wärme c der Reinstoffe zu erklären. Nach der Definition des Maß für die Wärmemenge Q gilt:
Q = c · m · (t2 - t1) = c · m · Δt
In Worten: um eine Menge m eines Reinstoffes von der Temperatur t1 auf die Temperatur t2 zu erwärmen, muss man die Wärmemenge Q zuführen. Die stoffspezifische Konstante c heißt die "spezifischen Wärme".
Durch umformen erhält man:
c = Q ⁄ (m · Δt) und
Δt = Q ⁄ (c · m).
Aus der letzten Gleichung erkennt man, dass die Temperaturänderung in einem Stoff bei konstanter Stoffmenge und Wärmezufuhr, die Temperaturänderung Δt umgekehrt proportional von der Stoffeigenschaft c abhängt.
Das heisst: bei konstanten Bedingungen ist die Temperaturänderung Δt kleiner, wenn die spezifische Wärme c größer ist, Δt ist größer, wenn c kleiner ist. So hat es Frau Foote beobachtet.
Betrachten wir die Messungen von Frau Foote. Da die spezifische Wärme von Luft cLuft = 1,01 kJ ⁄ (kg · K) größer ist als die von Kohlendioxid cCO2 = 0,846 kJ ⁄ (kg · K), wird bei gleicher zugeführter Wärmemenge Q die Temperatur im Kohlendioxid höher liegen als in der mit Luft gefüllten Röhre.
Die spezifische Wärme von Wasserdampf cWasser = 1,875 kJ ⁄ (kg · K) ist dagegen größer, und folglich wird Wasserdampf gesättigte Luft von der gleichen Wärmemenge nicht so stark erwärmt wie die Kohlendioxid-Atmosphäre: um Δt = 120 °F - 92 °F = 28 °F. Die Erwärmung der CO2-Atmosphäre ist dagegen Δt = 120 °F - 85 °F = 35 °F.
Nun sollen ja nicht Reingase betrachtet werden, sondern Gasmischungen wie Luft ⁄ CO2 und Luft ⁄ H2O. Die mittlere spezifische Wärme cm von Luft, die Fremdgase enthält, berechnet sich nach der Formel:
cm = (gLuft · cLuft + gCO2 · cCO2)
dabei ist gLuft, CO2 der Massenanteil der Luft und des CO2:
gLuft = mLuft ⁄ (mLuft + mCO2)
gCO2 = mCO2 ⁄ (mLuft + mCO2)
oder umgeformt und allgemein für beliebig viele Komponenten:
dabei ist mx die Masse der Komponente x und cx deren spezifische Wärmekapazität.
Mischt man also einem Gas ein anderes mit einer geringeren spezifische Wärme zu, so wird bei der Einstrahlung einer Wärmemenge die Temperatur der Mischung höher sein als die der reinen Hauptkomponente. Bei einer Mischung von Luft und 400ppm CO2 (das ist 0,0004 %!) steigt die Temperatur bei einer konstanten Wärmeeinstrahlung.
Die Werte, die Arrhenius extrapoliert hat, bezweifle ich; allerdings war zu seiner Zeit die Thermodynamik noch im Werden.
© Rainer Stumpe, URL: www.rainerstumpe.de/