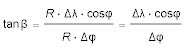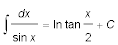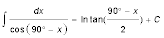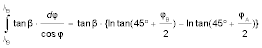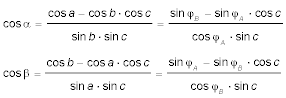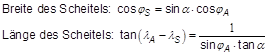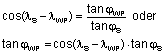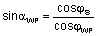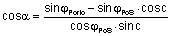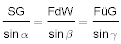Kursbestimmungen
Wenn man bei einem Törn weiss, wohin man will, bestimmt man zunächst den Kurs, mit dem man lossegeln will. Dabei unterscheidet man drei Berechnungsmethoden, die man je nach Entfernung vom Start- zum Zielort anwendet. Als nächstes interessiert bei der Törnplanung die Entfernung zwischen den beiden Orten. Die kann man aber in keinem der hier dargestellten Fälle aus der Karte ablesen: man muss immer rechnen.
- Für kurze Entfernungen, d. h. wenn man die Erdoberfläche als eben annehmen kann, verwendet man die Methode der mittleren Breite. Diese Berechnung entspricht dem Ablesen des Winkels zwischen der Nordrichtung und der Verbindungslinie der beiden Orte auf der Seekarte. Die Mercator-Projektion ist ja winkelgetreu, aber nicht flächengetreu (damit kann man den Kurs, aber nicht die Entfernung direkt aus der Karte entnehmen).
- Ist die Entfernung zu groß und muss man die Kugelgestalt der Erde berücksichtigen, rechnet man nach der Methode der Loxodrome. Die wird man anwenden, wenn Start- und Zielort nicht auf der gleichen Karte eingezeichnet sind.
- Schließlich für sehr weite Entfernungen — wenn man über mehrere Zeitzonen den kürzesten Weg sucht — verwendet man die Methode der Orthodrome.
- Einfluß der Strömung,
- Einfluß der Bewegung des Ziels (Treffpunktproblem),
- Besteckversetzung,
- Einfluß des Windes.
Aus den Ortskoordinaten nach der Methode der mittleren Breite
Für unsere Betrachtungen ist die Erde eine Kugel (was ja exakt nicht stimmt: sie ist kartoffelförmig). Wenn die Entfernungen nicht allzu groß sind, kann man die Erdoberfläche aber als eben betrachten, ohne einen zu großen Fehler zu machen; das Rechnen wird dann einfacher. In der Praxis nimmt man die einfachere Methode der mittleren Breite bis zu einer Entfernung von etwa 100 sm (andere Quellen sagen bis 10°, also 600 sm), darüber die Methode der der gemittelten Breite (Loxodrome), die von einer Kugelgestalt der Erde ausgeht. Nun sei nicht verschwiegen, dass die mit einer der beiden genannten Methoden ermittelte Entfernung nicht notwendigerweise die kürzeste ist. Auf der Kugel liegt die kürzeste Entfernung zwischen zwei Orten auf einem Großkreis, so dass man als dritte Berechnungsart noch die Großkreisnavigation (Orthodrome), nach den Regeln der sphärischen Trigonometrie, kennen sollte, wenn man nicht auf oder dicht an einem Meridian — also nach Norden oder Süden — segelt.
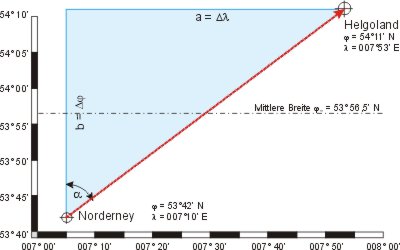
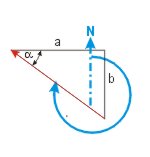
Für eine Fahrt von Norderney (53° 42′ N, 007° 10′ E) nach Helgoland (54° 11′ N, 007° 53′ E) kann man die Erde als eben ansehen. Es ergibt sich das linke Bild in rechtwinkligen Kartenkoordinaten.
Das blaue, rechtwinklige Dreieck hat die Katheten a Längendifferenz und b Breitendifferenz. Die Hypotenuse ist die Entfernung, der Winkel α der Kartenkurswinkel.
Wegen der Verzerrung der Mercatorprojektion entspricht die Bodenminute (ein 21.600stel des Erdumfangs) nur auf einem Meridian oder dem Äquator einer Seemeile. Die Breitenkreise sind Kleinkreise und haben einen geringeren Umfang, deshalb ist die Bogenminute dort kürzer und gehorcht der Beziehung Δx = Δλ·cos φ, wobei φ die geographische Breite ist. (Ableitung des Zusammenhanges siehe unter Sphärische Trigonometrie.) Zur Vereinfachung setzt man zur Entfernungsberechnung die mittlere Breite φm ein, die das arithmetische Mittel der beiden Ortsbreiten von Anfangs- und Endhafen der Reise ist
- φm = (53° 42′ + 54° 11′) ⁄ 2 = 53° 56,5′ = 53,94°.
- a = Δλ′ = Δλ · cos φm = 43′ · cos (53,94°) = 25′, (Δλ in Bogenminuten oder sm),
- b = Δφ = 29′ (in Bogenminuten oder sm).
Der Winkel α des Dreiecks ergibt sich aus der Definition des Tangens: tan α = Gegenkathete ⁄ Ankathete.
- tan α = (Δλ · cos φm) ⁄ Δφ = a ⁄ b = 25′ ⁄ 29′ = 0,862 ⇒ α = 41,6°.
Die Länge c der Hypotenuse (Abstand der Orte) erhält man aus der Definition des Sinus als
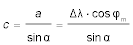 .
.
Beispielrechnung
Mit dem Rechenschieber führt man die Berechnung in zwei Schritten aus.
- Läufer über φm auf Skala S, 1 (oder 10) auf C unter Läuferstrich, Läufer auf Δλ verschieben (Ergebnis 1 merken); wenn Δλ′ kleiner als Δφ, auf Skala C unter den Läuferstrich (über das Ergebnis der Multiplikation) Läufer auf das Ergebnis der Division (1 oder 10 auf C) und auf T den Winkel ablesen. IstΔλ′ kleiner als Δφ, so liest man auf T den Cotangens (von rechts) ab.
- Sinus des Winkels merken und Läufer über Ergebnis 1 auf D einstellen und den gemerkten Sinuswert auf C unter den Läuferstrich stellen. Unter 1 (oder 10) auf C liest man auf D das Ergebnis ab. Da die Werte der Winkelfunktionen für Winkel < 90° immer kleiner als 1 sind, ist die Abschätzung der Kommastelle abhängig von Δλ in Bogenminuten.
Nun muss man nur noch aus dem Dreieckswinkel auf den Kartenkurs schließen.
Dabei muss man unterscheiden, ob die Längendifferenz der Ortskoordinaten größer ist als die Breitendifferenz, oder umgekehrt und ob man den Tangens oder den Cotangens abgelesen hat (wenn man die kleinere durch die größere Zahl teilt, erhält man mit dem Tangens den spitzesten Winkel!).
- a = Δλ < b = Δφ, Tangens ablesen,
- oder
- a = Δλ > b= Δφ, Cotangens ablesen.
Vom Dreieckswinkel zum rechtweisenden Kurs
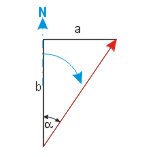
KaK = α
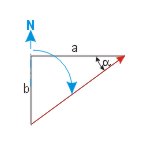
KaK = 90° - α
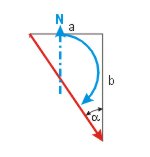
KaK = 180° - α
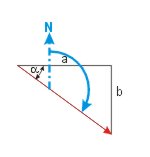
KaK = 90° + α
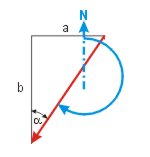
KaK = 180°+ α
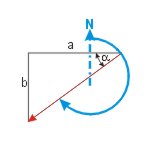
KaK = 270° - α
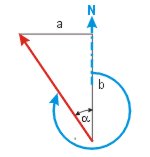
KaK = 360° - α
KaK = 270° + α
Aus den Ortskoordinaten nach der Methode der gemittelten Breite (Loxodrome)
Die oben dargestellte Berechnung der Längendifferenz in Bogenminuten in das Längenmaß Seemeilen liefert genaue Werte nur, solange die Änderung des Cosiunuswertes linear angesehen werden kann, also für kleine Breitendifferenzen. Eine genauere Methode, Bogenminuten auf Breitengraden in Seemeilen umzurechnen benutzt Kugelkoordinaten. Die verwendeten Formeln werden durch Integrieren der Differentialgleichung für die Kurslinie auf der Kugel erhalten.
Die Loxodrome schneidet alle Meridiane unter dem gleichen (Kurs-)Winkel. Wenn man sie über den Zielpunkt weiter fährt, bewegt man sich auf einer Spirale — man kommt also nicht am Startpunkt an, sondern nähert sich einem der Pole. Wenn der Winkel, unter dem die Loxodrome die Meridiane schneidet, 90° beträgt, bewegt man sich i. A. auf einem Breitenkreis (Kleinkreis, nur der Äquator ist auch ein Großkreis. Beträgt der Schnittwinkel 0°, so bewegt man sich auf einem Meridian (Großkreis).
Ableitung der Formeln für Kugelkoordinaten
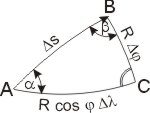
Die Erde wird in erster Näherung — und besonders für diese Berechnungen — als Kugel mit dem Radius R = 6.371 km angesehen. Die Kugelkoordinaten benutzen einen Vektor vom Erdmittelpunkt mit der Länge R des Erdradius, dessen Lage im Kugelraum durch die Längen- und Breitenwinkel angegeben wird. Man stellt sich nun vor, dass dieser Vektor von den Koordinaten des Startortes zu denen des Zielortes gedreht wird. Dabei muss der Breitenwinkel, der durchlaufen wird, der Differenz der Breitenkoordinaten und der Längenwinkel der Längendifferenz der Orte folgen. Im "ebenen" Dreieck gilt für die Entfernung (Hypotenuse) wieder die Tangensdefinition.
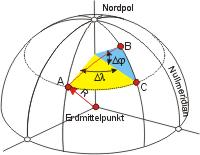
Die Länge der Strecke b entlang des Breitenkreises ist b = R · Δλ · cos φA, die Länge der Strecke a entlang des Meridians ist a = R · Δφ. (Δλ und Δφ im Bogenmaß!)
Damit ergibt sich für den Winkel β im Dreieck ABC (der Dreieckswinkel ist unabhängig von R):
In dieser Gleichung trennt man die Variablen und erhält:
Nun differenziert man diese Gleichung, d.h. man ersetzt die Änderung der Winkelkoordinaten des Vektors durch infinitesimale Änderungen.
Dann integriert man über den gesamten Winkeländerungsbereich. Das Integral der Differentialgleichung schaut man in einer Integraltabelle nach, meine Schulformelsammlung liefert:
Nun ist wegen der Beziehungen zwischen Winkelfunktionen sin x = cos (90° - x), sodass wir erhalten:
Die Integration der aufgestellten Differentialgleichung von λA bis λB liefert also:
Die Länge der Seite c = Δs ergibt sich aus der Definition des Sinus:
Kürzeste Strecke aus den Ortskoordinaten (Orthodrome)
Um auf der kürzesten Verbindungslinie von A nach B zu kommen, muss man sich auf der Kugel auf einem Großkreis bewegen. Für Segler hat das den Nachteil, dass der Großkreis jeden Meridian unter einem anderen Winkel schneidet, man also den Kurs kontinuierlich ändern muß (zur Berechnung der Loxodrome, die einen konstanten Kurs fahren läßt).
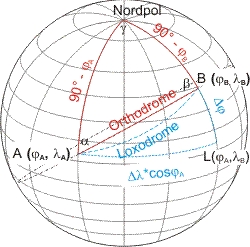
Die Orthodrome liegt definitionsgemäß auf einem Großkreis und ist eine Seite im sphärischen Poldreieck ABPol. Zur Berechnung der Länge der Kurslinie wendet man den Seitencosinussatz an in der Form:
- cos c = sin φA · sin φB + cos φA · cos φB · cos (λA - λB)
Zur Berechnung der Winkel im Poldreieck (die ja dem Start- und Ankunftskurs entsprechen) formen wir die Gleichungen des Seitensinussatzes, die α bzw. β enthalten, um in:
Für die Berechnung der Kurse zwischen Start und Ziel wird nun ein Fixpunkt auf dem Kurs-Großkreis definiert, der ein rechtwinkliges sphärisches Dreieck erzeugt, indem man vom Nordpol das (sphärische) Lot auf den Kurs-Großkreis fällt. Man nennt den Fixpunkt Scheitelpunkt, weil er dem Nordpol am nächsten liegt, also der "höchste" Punkt des Großkreises ist. (Liegt auf der Kurslinie Land, über das man nicht segeln kann, nimmt man die der Kurslinie an nächsten liegende Landspitze als Scheitel und macht die Berechnung zwei Mal.) Vom Scheitelpunkt aus kann man die Längen von Wegpunkten mit vorgegebener Breite auf dem Großkreis berechnen und den Winkel, unter dem der Großkreis den Meridian des Wegpunktes schneidet. Aus diesem ergibt sich der Steuerkurs am Wegpunkt.
Der Scheitelpunkt
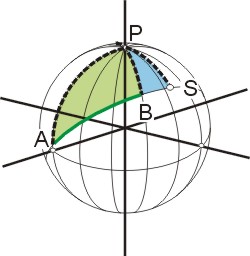
Der Scheitelpunkt ist eine Ecke in jedem der beiden rechtwinkligen Dreiecke APS und BPS. Im Dreieck APS sind bekannt der Winkel α und die Seite AP. Im Dreieck BPS sind bekannt die Seite BP und der Winkel PBS (= 180° - β). In beiden Dreiecken ist der Winkel bei S gleich 90°. Mit den drei bekannten Stücken eines Dreiecks kann man alle anderen berechnen.
Man stellt die Gleichungen für die unbekannten Seiten AS und BS auf (s. Neper´schen Regel und setzt sie in die Beziehung AS = AB + BS ein (AB ist die orthodrome Entfernung von A und B!). Nach ein bißchen Arithmetik erhält man:
Dabei sind φA die Breite des Start- oder Zielortes (oder eines anderen Ortes auf dem Großkreis), und α ist der Startwinkel.
Die Wegpunktkoordinaten
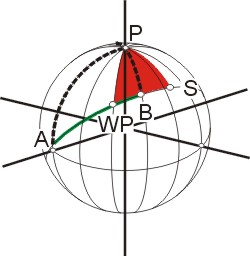
Da der Winkel PS(WP) definitionsgemäß ein rechter ist, sind alle roten Dreiecke, die einen Wegpunkt auf der (grünen) Kurslinie als Ecke haben, rechtwinklig. Bekannt sind in diesen Dreiecken der Winkel SP(WP) = λS - λWP, und die Seiten P(WP) = 90° - φWP und PS = 90° - φS. Mit der Neper´schen Regel findet man leicht die Formel:
Mit der analogen Überlegung erhält man als Formel für den Dreieckswinkel αWP beim Wegpunkt die Formel:
Beide Formeln eignen sich vorzüglich zur Berechnung mit dem Rechenschieber!
Beispielrechnung
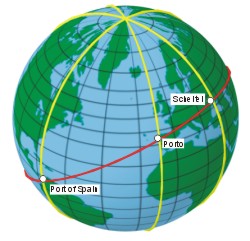
Die Fahrt soll von Porto in Portugal
- φPorto = 41° 09′ 28,0″ N = 41,1578°,
- λPorto = 008° 38′ W = -8,6333°
- (südliche Breiten und westliche Längen werden negativ angegeben)
nach Port of Spain auf Trinidad gehen
- φPoS = 10° 40′ 19,9″ N = 10,6722°,
- λPoS = 061° 32′ W = -61,5333°
Die Entfernung c beträgt cos c = sin φPorto · sin φPoS + cos φPorto · cos φPoS ·
cos (λPorto - λPoS) =
= sin 41,1578° · sin 10,6722° + cos 41,1578° · cos 10,6722° · cos (-8,6333° - (-61,5333°)) =
= 0,6581 · 0,1852 + 0,7529 · 0,9827 · 0,6032 = 0,1219 + 0,4463 = 0,5678.
⇒ c = 55,4° = 3323′ = 3.323 sm.
Der Startkurs in Porto ergibt sich aus der Berechnung:
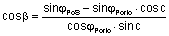
- oder linearisiert:
- cos β = [sin φPoS - sinφPorto · cos c] ⁄ cos φPorto · sin c =
- = [sin 10,6722° - sin 41,1578° · 0,4618] ⁄ cos 41,1578° · sin 55,4° =
- = [0,1852 - 0,6581 · 0,5678] ⁄ 0,7529 · 0,8231 =
- = - 0,1888 ⁄ 0,6197 = - 0,3042
- ⇒ β = 107,71°
Das Ergebnis ist β = 108°. Den Startkurs (relativ zur Nordrichtung) erhält man offensichtlich, wenn man den Dreieckswinkel von 360° abzieht: Startkurs = 360° - 108° = 252°.
Und der Ankunftskurs in Port of Spain wird berechnet aus der Formel:
Das Ergebnis ist α = 46,87°; der navigatorische Sachverstand sagt einem: der Steuerkurs ergibt sich durch Addition von 180°: Ankunftskurs = 180° + 46,9° = 227°.
Die Breite des Scheitelpunktes wird berechnet mit der Formel:
- cos φS = sin α · cos φPoS = sin 46,87° · cos 10,6722° = 0,7172;
⇒ φS = 44,1762°
Die Länge des Scheitelpunktes kann man nicht direkt berechnen (s. weiter oben auf dieser Seite), weil sie kein Winkel im Poldreieck ist. Aber das Dreieck APS ist ein rechtwinkliges Poldreieck, d. h. der Winkel ASP beim Scheitel ist 90°. Man findet also eine Beziehung für die Längendifferenz von Endpunkt zum Scheitel Δλ = λPoS - λS:
- tan (λS - λPoS) = cot α ⁄ sin φPoS =
- = cot 46,87° ⁄ sin 10,6722° = 0,937 ⁄ 0,185 = 5,065;
- ⇒ λS - λPoS = 78,83°, und daraus
- λS = 78,83° + (-61,53°) = 17,3°
Die Koordinaten des Scheitels sind also:
φS = 44° 10′ 34,3″ N,
λS = 017° 18′ E.
Berechnung von Wegpunkten auf der orthodromen Kurslinie:
Mit den Koordinaten des Scheitelpunktes und der vorgegebenen Länge λWP eines Wegpunktes kann man mit dem Rechenschieber bequem die Breite φWP des Wegpunktes nach der oben angegebenen Formel berechnen. Da eine Segelstrecke von 3.300 sm etwa 3 Wochen dauert, wurden die Längen für 25 Wegpunkte berechnet. Dann kann man täglich den Kurs ändern.
| Breite | Länge | rwK am WP |
| 41° 09′ 28,0″ | -008° 38′ 00,0″ | 252° |
| 40° 37′ 28,9″ | -010° 44′ 57,6″ | 251° |
| 40° 02′ 37,2″ | -012° 51′ 55,2″ | 250° |
| 39° 24′ 48,3″ | -014° 58′ 52,8″ | 248° |
| 38° 43′ 57,0″ | -017° 05′ 50,4″ | 247° |
| 37° 59′ 58,1″ | -019° 12′ 48,0″ | 246° |
| 37° 12′ 46,0″ | -021° 19′ 45,6″ | 244° |
| 36° 22′ 15,2″ | -023° 26′ 43,2″ | 243° |
| 35° 28′ 19,9″ | -025° 33′ 40,8″ | 242° |
| 34° 30′ 54,7″ | -027° 40′ 38,4″ | 240° |
| 33° 29′ 54,1″ | -029° 47′ 36,0″ | 239° |
| 32° 25′ 12,8″ | -031° 54′ 33,6″ | 238° |
| 31° 16′ 46,0″ | -034° 01′ 31,2″ | 237° |
| 30° 04′ 29,5″ | -036° 08′ 28,8″ | 236° |
| 28° 48′ 19,7″ | -038° 15′ 26,4″ | 235° |
| 27° 28′ 14,1″ | -040° 22′ 24,0″ | 234° |
| 26° 04′ 11,3″ | -042° 29′ 21,6″ | 233° |
| 24° 36′ 11,1″ | -044° 36′ 19,2″ | 232° |
| 23° 04′ 15,2″ | -046° 43′ 16,8″ | 231° |
| 21° 28′ 27,0″ | -048° 50′ 14,4″ | 230° |
| 19° 48′ 52,1″ | -050° 57′ 12,0″ | 230° |
| 18° 05′ 38,3″ | -053° 04′ 09,6″ | 229° |
| 16° 18′ 55,8″ | -055° 11′ 07,2″ | 228° |
| 14° 28′ 57,8″ | -057° 18′ 04,8″ | 228° |
| 12° 35′ 59,7″ | -059° 25′ 02,4″ | 227° |
| 10° 40′ 19,9″ | -061° 32′ 00,0″ | 227° |
Wenn man mit dem Rechenschieber diese Berechnung ausführt, legt man zunächst die Längen der gewünschten Wegpunkte in einer Tabelle fest, und berechnet im Kopf die Differenz λS - λWP und trägt des Cosinus dieser Differenz in die Tabelle ein. Da die Breite φWP des Wegpunktes nach der Formel
- tan φWP = tan φS · cos(λS - λWP)
berechnet wird, in der tan φS eine Konstante für die Orthodrome ist, stellt man den Läufer über den Wert des Tangens der Scheitelbreite, und schiebt den Wert für cos(λS - λWP) aus der Tabelle auf der Zunge unter den Läuferstrich. Unter der 1 (oder 10) auf der Zunge findet man auf der Tangensskala den Winkel der Breite des Wegpunktes. Wenn man dessen Cosinus gleich notiert, kann man den zugehörigen Kurswinkel nach der Formel leicht auszurechnen:
- sin α = cos φS ⁄ cos φWP
| λWP | λS - λWP | cos(λS-λWP) | tan φWP | φWP | cos φWP |
| -008,63° | 25,93° | 0,8993 | 0,8738 | 41,1° | 0,7530 |
| -010,75° | 28,05° | 0,8825 | 0,8575 | 40,6° | 0,7591 |
| -012,87° | 30,17° | 0,8646 | 0,8401 | 40,0° | 0,7657 |
| -014,98° | 32,28° | 0,8454 | 0,8215 | 39,4° | 0,7727 |
| -017,10° | 34,40° | 0,8251 | 0,8017 | 38,7° | 0,7802 |
| -019,21° | 36,51° | 0,8037 | 0,7809 | 38,0° | 0,7881 |
| -021,33° | 38,63° | 0,7812 | 0,7591 | 37,2° | 0,7965 |
| -023,45° | 40,75° | 0,7576 | 0,7361 | 36,4° | 0,8053 |
| -025,56° | 42,86° | 0,7330 | 0,7122 | 35,5° | 0,8145 |
| -027,68° | 44,98° | 0,7074 | 0,6873 | 34,5° | 0,8241 |
| -029,79° | 47,09° | 0,6808 | 0,6615 | 33,5° | 0,8340 |
| -031,91° | 49,21° | 0,6533 | 0,6348 | 32,4° | 0,8443 |
| -034,03° | 51,33° | 0,6249 | 0,6072 | 31,3° | 0,8548 |
| -036,14° | 53,44° | 0,5956 | 0,5788 | 30,1° | 0,8655 |
| -038,26° | 55,56° | 0,5656 | 0,5495 | 28,8° | 0,8764 |
| -040,37° | 57,67° | 0,5347 | 0,5196 | 27,5° | 0,8874 |
| -042,49° | 59,79° | 0,5032 | 0,4889 | 26,1° | 0,8984 |
| -044,61° | 61,91° | 0,4709 | 0,4576 | 24,6° | 0,9093 |
| -046,72° | 64,02° | 0,4380 | 0,4256 | 23,1° | 0,9201 |
| -048,84° | 66,14° | 0,4045 | 0,3931 | 21,5° | 0,9307 |
| -050,95° | 68,25° | 0,3705 | 0,3600 | 19,8° | 0,9409 |
| -053,07° | 70,37° | 0,3360 | 0,3264 | 18,1° | 0,9506 |
| -055,19° | 72,49° | 0,3010 | 0,2924 | 16,3° | 0,9598 |
| -057,30° | 74,60° | 0,2655 | 0,2580 | 14,5° | 0,9683 |
| -059,42° | 76,72° | 0,2298 | 0,2232 | 12,6° | 0,9760 |
| -061,53° | 78,83° | 0,1937 | 0,1882 | 10,7° | 0,9828 |
Auf der Orthodrome ändert man den Kurs im Verlaufe des Törns kontinuierlich von 252° bis 227°. Berechnet man den Kurs nach der Loxodrome, beträgt der konstante Kurswinkel 237°. Die Entfernung zwischen Porto in Portugal und Port of Spain auf Trinidad ist bei konstantem Kurs 3.348 sm, auf der Orthodrome nur 3.323 sm. Der Entfernungsunterschied beträgt also etwa 25 sm! Aber da man auf so einer Reise ja wenig zu tun hat, kommt die Rechnerei gelegen — für knapp einen Tag Zeitersparnis.
Interessanter wird der Unterschied beim Fliegen. Von New York (40° 43′ N, 74° 0′ W) nach Frankfurt ( 50° 7′ N, 8° 41′ O), oder nach Tokyo (35° 41′ N, 139° 46′ O) beträgt die Einsparung je ungefähr 70 sm. Aber auf diesen Strecken kann man nicht segeln.
Fahrt in der Strömung
Fährt man z. B. im Tidenrevier, wird man in aller Regel mit dem Tidenstrom konfrontiert. Da man die Strömung mit Bordmitteln nicht messen kann, entnimmt man ihre Richtung und Geschwindigkeit der Karte bzw. dem Gezeitenatlas. Da die Stromgeschwindigkeit abhängig ist vom Alter der Gezeit, muss man ein wenig rechnen oder einfach schätzen.
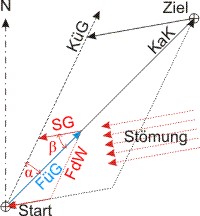
Die nebenstehende Skizze stellt das Problem dar. Vom Startort zum Zielort entnimmt man den Kartenkurs KaK der Karte, oder berechnet ihn aus den Kartenkoordinaten der beiden Orte. Die Strömung — in der Skizze kommt sie schräg von vorn — beeinflusst nicht nur die Richtung (KüG), die das Boot tatsächlich nimmt, sondern auch seine wirkliche Geschwindigkeit (FüG). Um überhaupt am Zielort anzukommen, muss man also gegen die Strömung steuern. Die Kurskorrektur kann man natürlich berechnen.
Die roten Pfeile im Parallelogramm mit der FüG auf der Verbindungslinie Start-Ziel als Diagonale stellen die Einheitsvektoren dar. Ihre Länge entspricht der Strecke, die das Boot in einer Stunde zurück legt. Wir erkennen ein Dreieck mit den bekannten Seiten FdW und Stromgeschwindigkeit, und dem bekannten Winkel der Strömungsrichtung β. Gesucht sind im Vektordreieck die Seite FüG und der Winkel α.
Die beiden kongruenten Dreiecke sind im allgemeinen schiefwinklig, d. h. kein Winkel ist recht (= 90°), allerdings sind nicht alle Winkel notwendiger Weise spitz (< 90°). Man kann also zur Berechnung prinzipiell den Sinussatz anwenden. Da der bekannte Winkel β der längeren der beiden bekannten Seiten Strom und FdW gegenüber liegt, handelt es sich um das dritte Grundproblem (es ist sicher anzunehmen, dass die Fahrt durch das Wasser schneller ist als die Strömungsgeschwindigkeit, also liegt β der längeren Seite gegenüber).
-
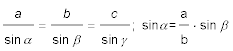
- Mit dem gesuchten Winkel α lautet die Formel also:
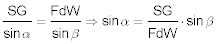
Die FüG ergibt sich nach dem Sinussatz mit dem Winkel γ, der sich aus der Winkelsumme im Dreieck und der Summe der beiden anderen Winkel ergibt: γ = 180° - (α + β). Da er i. d. R stumpf (γ gt; 90°) ist, nimmt man mit dem Rechenschieber den Supplementwinkel 180° - γ: γ = α + β. Zusammengefaßt verwendet man den Sinussatz in der Form:
und erhält die Länge des Vektors FüG als Strecke, die man pro Stunde tatsächlich zurück legt.
Beispielrechnung
Ein Boot segelt mit FdW = 6 kn (FdW) den rwKaK = 45° durch einen Kanal zwischen 2 Inseln, in der ein Strom mit SG = 2,5 kn in rwRichtung 95° versetzt zu einem 30 sm entfernten Ort. Welchen Kurs muss das Boot zum Ziel steuern, und wie lange braucht es zum Ziel?
Besonders einfach ist die Rechnung mit einem Unique Navigator, der hat nämlich Sinus- und Tangensskalen auf dem Körper und auf der Zunge. Man kann also durch Sinus bzw. Tangens dividieren. Man bildet also die Verhältnisse FdW ⁄ sin α = SG ⁄ sin α auf dem Rechenschieber ab:
- Man stellt den sin β unter die FdW,
- schiebt den Läufer auf die Strömungsgeschwindigkeit,
- und liest auf der Sinuskala den Wert für α ab.
-

- bewegt man den Läufer auf die Winkelsumme β + α auf der Sinusskala und liest die FüG ab.
-
und hat mit einer Einstellung beide Aufgaben gelöst!
- Man liest ab:
- α = 18,6°,
- WüG = 7,3.
Mit FüG = FdW ⁄ WüG · FdW = 6 ⁄ 7,3 · 6 = 4,94 erhält man die tatsächliche Geschwindigkeit über Grund zu 5 sm.
Etwas umständlicher ist die Rechnung mit einem gewöhnlichen Rechenschieber. Man muss die Gleichungen des Sinussatzes umformen:
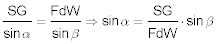
- Man stellt die "10" der C-Skala über "50°" auf der Sinusskala und schiebt den Läufer über "2,5" auf C.

- unter den Läuferstrich schiebt man die "6" der Zunge, und liest unter "10" auf C den Winkel auf der Sinusskale ab: α = 18,6°.

Zur Berechnung der FüG lösen wir den Sinussatz nach FüG auf:
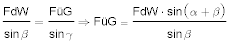
- Zuerst lesen wir den sin β = sin 50° = 0,766 auf dem Rechenschieber ab und notieren den Wert, dann stellen wir die "10" der Zungenskala C über 69° auf der Sinusskala und schieben den Läufer auf die "6" auf C
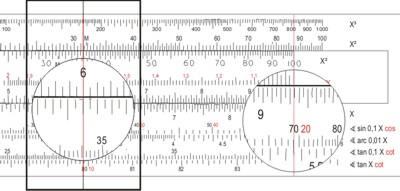
- unter den Läuferstrich stellen wir 0,766 auf C und lesen auf D die FüG = 7,3 sm ab.
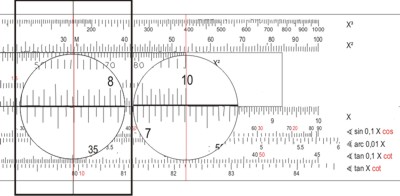
Mit einem üblichen Rechenschieber muss man zwar ein Zwischenergebnis aufschreiben, aber die Rechnung ist trotzdem sehr einfach und schnell.
Der wahre und der scheinbare Wind
Bereits im ersten Segelkurs lernt man, dass es drei Winde gibt: den wahren, den scheinbaren und den Fahrtwind. Gesegelt wird nach dem scheinbaren Wind — jedenfalls, was die Segelstellung angeht. In den Lehrbüchern findet man dann ein Diagramm und die Erklärung, der scheinbare Wind ergäbe sich durch Vektoraddition aus Fahrt- und wahrem Wind.
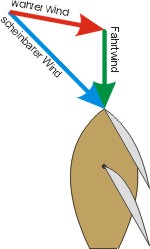
Der wahre Wind bläst aus einer Richtung mit einer Stärke, die man beim stillliegen beobachtet. Den Fahrtwind fühlt man, wenn man bei Flaute unter Motor fährt. Bewegt man sich in einem Windfeld, dann kann man die beiden „Winde“ nicht getrennt wahrnehmen: es ergibt sich der scheinbare Wind als Mischung der beiden vorgenannten Luftbewegungen.
Da „Wind“ beschrieben wird mit Richtung und Stärke, kann man ihn durch einen Pfeil symbolisieren: der Winkel zu einer vorgegebenen Referenzrichtung (beim Segeln die Nordrichtung) gibt die Windrichtung an (die Pfeilspitze zeigt in die Richtung, in die der Wind bläst!), die Länge des Pfeiles die Windstärke.
Solche Pfeile nennt man Vektoren, und man kann nach den Regeln der Vektoralgebra mit ihnen „rechnen“. Grafisch addiert man Vektoren, in dem man parallel verschiebt bis das Ende des einen mit der Spitze des anderen zusammenfält. Das Additionsergebnis ist dann der Pfeil vom Ende des zweiten zur Spitze des ersten Vektors. (Die nebenstehende Abbildung ist als Prinzipbild für die Vektorzerlegung gedacht; sie gibt nicht die wahren Verhältnisse wieder.)
Mit den Augen eines Trigonometriekenners sieht man ein schiefwinkliges Dreieck mit drei Seitenlängen (den Windstärken) und drei Winkeln (den relativen Windrichtungen). Man könnte also mit dem Rechenschieber rechnen (wenn ’mal die Windanlage an Bord ausgefallen ist).
In dem Dreieck kennt man drei Stücke: den Winkel α (das ist die beobachtete Windrichtung relativ zur Bootsachse d. i. zum rechtweisenden Kurs rwK), die Stärke des Fahrtwindes (das ist die Geschwindigkeit im Wasser FdW) und die Stärke des scheinbaren Windes (die misst man mit dem Anemometer an Bord). Gesucht sind in der Regel Richtung und Stärke a des wahren Windes. Die Richtung (zu Nord) ergibt sich aus dem Winkel β, der ja der Kurswinkel rwK ist.
Wir kennen also zwei Seiten und den eingeschlossenen Winkel — eine typische Aufgabe für den Cosinussatz:
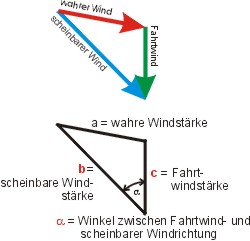
Für den Rechenschieber einfacher wird die Rechnung, wenn man diese Formel umformt. Man ergänzt mit +2·b·c und -2·b·c und stellt etwas um:
- a2 = (b2 + 2·b·c + c2) - (2·b·c - 2·b·c·cos α) =
- = (b + c)2 - 2·b·c·(1 + cos α)
- Da (1 + cos α) = 2·cos2(α ⁄ 2) erhält man:
- a2 = (b + c)2 - 4·b·c·cos2(α ⁄ 2)
Mit dieser Formel muss man nur (b + c)2 und 4·b·c·cos2(α ⁄ 2) notieren. Den Winkel β zwischen Kurs rwK und wahrem Wind berechnet man mit dem Sinussatz (die Quotienten aus dem Sinus jeden Winkels und der gegenüberliegenden Seite sind gleich).
Beispielrechnung
Ein Boot segelt mit 6 kn auf Kurs rwK = 35°. Der scheinbare Wind weht mit 11 kn (4 Beaufort) aus 330°. Aus welcher Richtung und mit welcher Stärke bläst der wahre Wind?
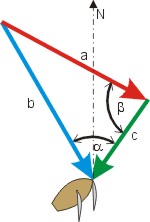
Der Winkel α beträgt α = (360° - 330°) + 35° = 65°. Mit α und den Seiten b (Stärke des scheinbaren Windes) und c (Stärke des Fahrtwindes) berechnen wir die Seitenlänge a, die die Stärke des wahren Windes repräsentiert.
- a2 = (b + c)2 - 4·b·c·cos2(α ⁄ 2)
Der erste Term der Gleichung ergibt (b + c)2 = (11 + 6)2 = 172 = 289. Den cos(α ⁄ 2) = cos(65° ⁄ 2) = cos 32,5° = 0,84 quadrieren wir (= 0,71), multiplizieren mit 4 · 11 · 6 und erhalten 187,8. Die Differenz der beiden Terme ist a2 = 289 - 187,8 = 101,4; a = 10,1. ⇒ Der wahre Wind bläst mit 10 kn = 3 Bft.
Nach dem Sinussatz ist sin β = b ⁄ a · sin α = 11 ⁄ 10,1 · sin 65° = 0,987; β = 80°. Damit ist der Winkel γ zwischen scheinbarem und wahrem Wind 180° - 65° - 80° = 35°, und der wahre Wind kommt aus 330° - 35° = 295° (achterlicher als der scheinbare).
Berechnung von Richtung und Stärke des scheinbaren Windes aus Kurs und wahrem Wind
Interessanter könnte die Frage sein, mit welchem Kurs kann ich bei maximal möglicher Geschwindigkeit bei gegebener (wahrer) Windstärke und -richtung segeln? Die meisten Yachten fahren mit 80° bis 100° zum scheinbaren Wind am schnellsten. Die Frage bei der Törnplanung ist ja oft, wie steuere ich optimal, wenn das Ziel gegen den vorhergesagten Wind liegt?
Im Grunde ist das eine Optimierungsaufgabe. Man berechnet den Kurs bei einer Geschwindigkeit, die man erreichen mit 80° zum scheinbaren Wind erreichen kann. Stellt fest, wie weit man beim Kreuzen fahren muss und wie lange man zu dieser Strecke braucht. Im zweiten Schritt nimmt man den Kurs höher am Wind, und berechnet, wie lange man bei der dadurch reduzierten Geschwindigkeit brauchen wird. Nach ein paar Iterationen wird man einen optimalen Kurs gefunden haben.
Messung in der Praxis
Dieses Beispiel ist analog der Anleitung von Snodgrass "Wind and Drift Problems" gestaltet. Ein Besucher, Herr C. N., dieser Seite wies mich darauf hin, dass man bei einer Wende die Richtung des wahren Winds auf dem Kompass im den Augenblick ablesen kann, wenn der Wind genau von vorne kommt. Die Geschwindigkeit des wahren Winds erhält man aus der Differenz der Anzeigen von Logge und Anemometer.
Besteckversetzung
Beim Segeln — besonders im Gezeitenrevier mit seinen Gezeitenströmungen — wird man bei einer Peilung nach längerem Koppeln feststellen, dass der beobachtete Ort Ob und der gekoppelte Ort Ok nicht übereinstimmen. Der Grund liegt in der Wind- und Stromversetzung, die man beim Koppeln nicht quantitativ berücksichtigen konnte. Durch das Bestimmen der Besteckversetzung kann man (wenn die Stromversetzung bekannt ist) ein Gefühl für die Windversetzung des Bootes bekommen.
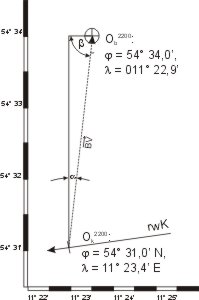
Die Besteckversetzung BV ist Richtung und Entfernung des gekoppelten Schiffsortes Ok zum beobachteten Ort Ob. Die Skizze zeigt das rechtwinklige Dreieck (γ = 90°), in dem die Berechnung durchgeführt wird. Es ist außer γ kein Dreieckswinkel bekannt. Die Berechnung von Kurs und Entfernung aus den Koordinaten der Orte liefert die Lösung. Die Rechnung liefert den Winkel der BV αBV, der sich mit β zum Gegenkurs des rwK ergänzen muss.
Die Lösung des Problems ist das Berechnen von Richtung und Entfernung der beiden Orte Ob und Ok nach der bekannten Methode der mittleren Breite.
(Diese Aufgabe wird von Burns Snodgrass in seinem Buch Teach Yourself the Slide Rule für die Flugzeugnavigation erläutert: dort gibt es ja nur den Wind, der das Flugzeug ablenkt. Deshalb bekommt man dort auch die Versetzung für die Kurskorrektur zum weiteren Koppeln heraus. Beim Navigieren eines Segelbootes findet man nur die Summe der Strom- und Windversetzung.)
Beispielrechnung
Eine Jacht steuert den Kurs rwK = 262° und bestimmt den Schiffsort durch Peilung:
- Ob: 2200: φ = 54° 34,0′ N, λ = 011° 22,9′ E.
Der gekoppelte Ort hat die Koordinaten:
- Ok: 2200: φ = 54° 3l,0′ N, λ = 011° 23,4′ E.
Bestimme die Besteckversetzung.
Berechnen wir zunächst die Richtung und die Entfernung nach der Methode der mittleren Breite.
| Geogr. Breite φ | Geogr. Länge λ | |||
|---|---|---|---|---|
| in ° und ′ | in Dezimal° | in ° und ′ | in Dezimal° | |
| Koordinaten Ok | 54° 31,0′ | 54,517° | 11° 23,4′ | 11,390° |
| Koordinaten Ob | 54° 34,0′ | 54,567° | 11° 22,9′ | 11,382° |
| Unterschied (in °) | 0° 03′ | 0,050° | 0° 00,5′ | 0,008° |
| Unterschied (in ′) | 3′ | 3 sm | 0,5′ | 0,5 sm |
| mittlere Breite | 54° 32,5′ | 54,542° | ||
Berechnen des Winkels αBV aus dem Verhältnis von Längendifferenz und Breitendifferenz, wobei man die kleinere Zahl durch die größere dividiert und aus tan αBV den Winkel αBV = 5,3° erhält.
tan αBV = (Δλ · cos φm) ⁄ Δφ = (0,008° · cos 54,542°) ⁄ 0,050° = 0,0046° ⁄ 0,05° = 0,093 ⇒ αBV = 5,3°
- β = (rwK - 180°) - αBV = (262° - 180°) - 5,3° = 76,7°
- α = 180° - 76,7° - 90° = 13,3°
- sin αBV = Δλ ⁄ BV ⇒
- BV = Δλ ⁄ sin αBV = 0,3′ ⁄ sin 5,3° = 3,24 sm
Die Besteckversetzung um 22:00h beträgt 3,24 sm in Richtung 5° 18′ .
Das Treffpunktproblem
Das Handbuch "Seemannschaft", 24. Auflage, erläutert an dem folgenden Beispiel, wie man das Problem, einem bewegliches Ziel zu begegnen, durch Kartenkonstruktion lösen kann. Viel einfacher geht das mit dem Sinussatz und dem Rechenschieber.
Eine Motoryacht hat um 12.10h über Sprechfunk an Norddeich Radio gemeldet, dass sie infolge Motorschadens in Not sei; um 12:15h gibt sie ihren Standort bei Leucht-Heultonne 1 an (φ = 53° 52,1′ N und λ = 007° 58,9′ E). Sie teilt gleichzeitig mit, dass sie bei ESE-Windstärke 6 und ablaufendem Wasser mit 2,5 kn in Richtung rw 290° treibe. Welchen Kurs muss eine andere Yacht, die um 12:15h bei der Leuchttonne Scharhörnriff steht (φ = 53° 58,6′ N und λ = 008° 08,8′ E), bei einer Fahrt von 8 kn steuern, und wie viel Zeit wird sie benötigen, um die in Not befindliche Yacht zu treffen?
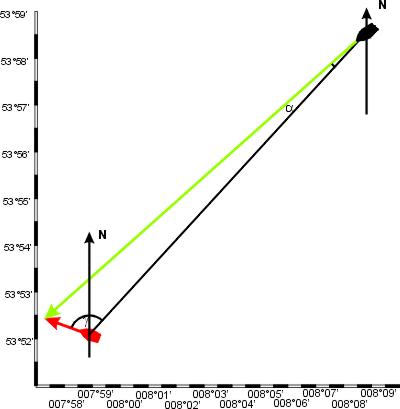
In so einem Falle wird man zunächst die beiden Standorte in der Karte eintragen und die Peilung zum Havaristen feststellen. In der Skizze erkennt man sofort, dass die Fahrtstrecke, bzw. die Fahrtgeschwindigkeit des Helfers, zum Treffpunkt (grün) sich zu der Strecke (bzw. die Abtreibgeschwindigkeit), um die die rote Jacht abgetrieben wird (rot), verhält wie sin α zu sin γ. Der Winkel zwischen Südrichtung und Peilung der Jacht um 12:15h (42°, berechnet) und der Winkel zwischen Peilungslinie und Nordrichtung beim Havaristen ist identisch (Winkel an Parallelen!). Damit ist der Winkel γ gleich 360° - Triftwinkel + Peilung = 360° - 290° + 42° = 112°. Daraus errechnet man den Winkel α, um den die Peilung um 12:15h zu korrigieren ist um den Steuerkurs zu erhalten. In der ersten Berechnung kann man die FdW (8 kn) des Helfers als seine Geschwindigkeit einsetzen.
In einem zweiten Schritt wird dann die FüG des Helfers, die durch Strom- und Windbeschickung (2,5 kn, 290°) sich von der FdW unterscheiden wird, berechnet und die erste Rechnung mit realistischen Geschwindigkeiten wiederholt.
|
1. Schritt Der Winkel α ergibt sich aus der Gleichung:
|
2. Schritt
|
Die Kurse des Havaristen und den Steuerkurs trägt man nun in die Karte ein, misst die Entfernung vom Standort zum Schnittpunkt und kann mit der FüG die voraussichtliche Zeit bis zum Treffen ausrechen. Die Entfernung der Schiffsorte um 12:15 h wird mit 8,74 sm berechnet; es gibt keine einfache Möglichkeit, die Entfernung zum Treffpunkt auszurechnen: das macht man mit der Karte.
Wenn während der Fahrt zum Treffpunkt der Wind dreht oder sich die Stromrichtung und -geschwindigkeit ändern, muss man die Berechnungen erneut vom Koppelort ausführen. Nach "Seemannschaft" wird zeichnerisch der Kurs zu 239° ermittelt. Dieser Kurs enthält aber noch keine Korrektur durch Beschickung, die im Rechenbeispiel gleich der Abdrift des Havaristen gesetzt wurde. Der durch Abdrift — wie sie hier festgestellt wurde — auf die Entfernung von ca. 10 sm verursachte Fehler beträgt knapp 0,5 sm.
In Burns Snodgrass Anleitungsbuch Teach Yourself the Slide Rule wird das Treffpunktproblem ebenfalls ausgeführt.
© Rainer Stumpe, URL: www.rainerstumpe.de/
Datenschutzerklärung