Der Aufbau des Rechenschiebers
Bauteile und Skalenanordnung
Der zeitgenössische Rechenschieber hatte drei Teile:
- den Körper,
- die Zunge,
- den Läufer.
Auf dem Körper und der Zunge sind die (logarithmischen) Rechenskalen angeordnet; dabei sind zusätzliche Skalen auf der Rückseite der Zunge angeordnet. Der Läufer erleichtert das Einstellen und Ablesen von Zahlenwerten. Zur Handhabung und Pflege des Rechenschiebers gibt die Anleitung zum Schulrechenstab Hinweise.
Der erste von Seth Partridge in seinem Buch "The Description and Use of an Instrument Called the Double Scale of Proportion" beschriebene Rechenschieber bestand aus drei Linealen (die beiden äußeren waren verbunden und bildeten den Körper), auf denen die Skalen eingraviert waren: auf allen drei Teilen die Lines of Numbers, auf dem mittleren die Line of Sines und die Line of Tangents.
[Auszug mit seiner Beschreibung des Rechenschiebers]
| Name | Einteilung | Bezeichnung |
|---|---|---|
| logarithmische Skalen | 1 - 10 | Körper: D Zunge: C |
| log. Quadratskalen | 1 - 100 | Körper: A Zunge: B |
| log. Kubikskala | 1 - 1000 | Körper: K |
| inverse log. Skala | 10 - 1 | Zunge: CI |
| Sinus/Cosinus-Skala | 5,5° - 90° | Körper bzw. Zunge: S |
| Tangens/Cotangens-Skala | 5,5° - 45° | Körper bzw. Zunge: T |
| Logarithmusskala | 0 - 1 | Zunge: L |
| Arcus-Skala | 0,55° - 5,5° | Körper: ST |
Man unterscheidet — bezogen auf die Art und Anordnung der Skalen — drei Grundmodelle:
- System Mannheim (nach dem französischen Mathematiker Amédée Mannheim, der um 1850 die erste Standardisierung der Rechenschieber mit transparentem Läufer vorschlug). Diese Rechenschieber sind selten.
- Skalen: C und D, A und B, S und T.
- System Rietz (nach dem deutschen Ingenieur Max Rietz, der 1902 das System Mannheim um die Sinus- und die Tangensskala auf der Rückseite der Zunge einführte).
- System Darmstadt (nach dem Mathematiker an der TU Darmstadt Alwin Oswald Walther, der 1934 die Skalen um die pythagoreischen Skala √(1 - x2) ergänzte und die Sinus- und die Tangensskala auf die Vorderseite des Körpers verlegte. Die Rückseite der Zunge trug drei Exponentialskalen ex trug.)
Die reinen Ausführungen sind alle älter, oder als Werbegeschenke verteilt worden. Daneben waren viele abgeleitete Systeme mit Sonderskalen und abgeleiteten Anordnungen erhältlich, die für Sonderanwendungen (Elektro, Finanzen, Navigation, Chemie u. v. a. m.) optimiert waren.
Ablesen der Skalen
Damit man Strecken addieren kann, müssen Skalen, die zum Rechnen dienen, auf Körper und Zunge angeordnet sein. Skalen, die es nur einmal gibt sind nur zum Ablesen von Werten, z. B. der Winkelfunktionen.
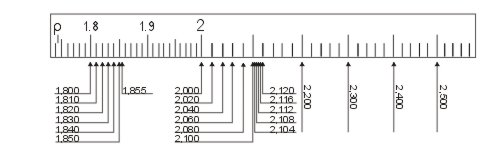
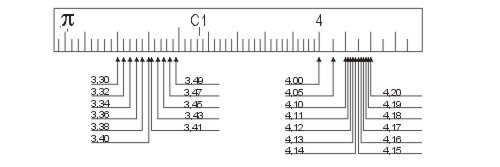
Die logarithmische Einteilung der Skalen führt dazu, dass die Strecke zwischen den Zahlen 1 und 2 auf C oder D wesentlich größer ist als die zwischen 9 und 10. Entsprechend kann man im Bereich von Zahlen bis 3 mit mehr signifikanten Stellen rechnen als mit den größeren Zahlen im rechten Teil des Rechenschiebers.
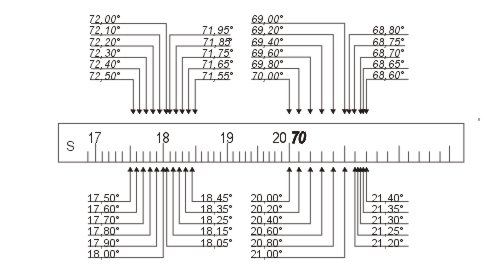
Das gilt auch für die Winkelfunktionsskalen, z. B. für S:
Eine hübsche Anwendung der Quadratskalen A und B ist die Berechnung von Geschwindigkeiten aus Fahrtstrecke (in km oder sm) und Fahrtzeit (in Minuten).
Die pythagoreische Skala P
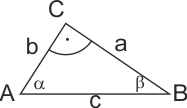 Die pythagoreische Skala P ermöglicht sehr elegant die Stücke des rechtwinkligen Dreiecks zu berechnen, wenn man nur eine Kathete und die Hypotenuse kennt. Nach dem Satz des Pathagoras: a2 + b2 = c2. Löst man diese Gleichung nach einer Kathete auf: a2 = c2 - b2 und dividiert durch c2 erhält man:
Die pythagoreische Skala P ermöglicht sehr elegant die Stücke des rechtwinkligen Dreiecks zu berechnen, wenn man nur eine Kathete und die Hypotenuse kennt. Nach dem Satz des Pathagoras: a2 + b2 = c2. Löst man diese Gleichung nach einer Kathete auf: a2 = c2 - b2 und dividiert durch c2 erhält man:
Setzt man c = 1 und zieht die Wurzel erhält man:
Da nach der Definition a ⁄ c = sin α und b ⁄ c = sin β ist und im rechtwinkligen Dreieck β = 90° - α gilt, kann man auch schreiben:
Diese Gleichung ist transzendent, d. h. man kann nicht durch Einsetzen einer der Variablen α oder β die andere ausrechnen. Auf eine solche Gleichung ist schon Johannes Kepler gestoßen, als er die Kepler-Gleichung ableitete. Er mußte noch die rechte und die linke Seite der Gleichung ausrechnen und schauen, für welche Wertepaare sie erfüllt ist. Alwin Walther erstellte also eine Tabelle der Werte von √ (1 - cos2 α) mit 0° > α < 90°, und zeichnete sie gleich lang mit der Sinus-Skala auf den Rechenschieber: die pythagoreische Skala war geboren. Ebenso konnte der die gleiche Zahlenreihe mit der C- bzw. der D-Skala des Rechenschiebers in Verbindung bringen.
Bei Rechnungen im rechtwinkligen Dreieck sucht man also den Wert von √(1 - x2) auf der Skala P zum Verhältnis a ⁄ c = sin α, d. h. man teilt die kleinere Zahl durch die größere, und multipliziert diesen mit c; so erhält man die zweite Kathete b. Auf dem Rechenschieber mit geeigneter Skalenanordnung findet man auch die Größe des zwichen a und c eingeschlossenen Winkels β mit einer Einstellung. Der zweite Winkel α folgt aus der Summe der Winkel im rechtwinkligen Dreieck: α + β = 90°.
Es sei a = 18,3 und c = 21,7 so teilt man mit den Skalen C und D 18,3 ⁄ 21,7 = 0,844.
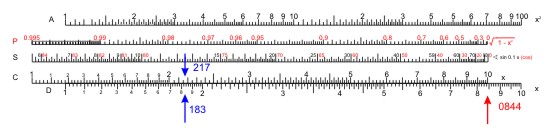
Dann stellt man die Zunge in die Ausgangsstellung und schiebt den Läufer auf 0,844 auf der Skala P. In dieser Einstellung liest man den Winkel β auf der Sinus-Skala S ab: 32,4°. Der zweite Winkel hat die Größe α = 90° - 32,4° = 57,6°.

Nun stellt man die "10" auf der Zungenskala unter den festgehaltenen Läuferstrich und verschiebt den Läufer auf der Skala C über c = 21,7. Unter dem Läuferstrich liest man auf der Skala D das Ergebnis ab: b = 11,63.
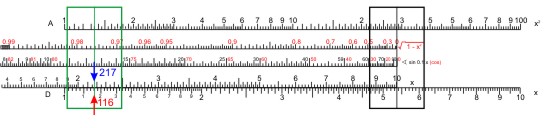
Dieses Verfahren geht wesentlich schneller als das Quadrieren zweier Zahlen, Bilden der Differenz und Wurzelziehen aus dem Ergebnis — aber es funktioniert nur mit dem Rechenschieber. Je nach Anordnung der Skalen auf dem Rechenschieber kann man auch die Winkelfunktionen ebenso bequem zur Berechnung der Grundaufgaben im rechtwinkligen Dreieck verwenden.
Weitere Anwendungen der pythagoreischen Skala sind in diversen Rechenschieberanleitungen. und aus der Seite der Rechenschieber-Sammler.