Wenn man alle möglichen Dreiecke berechnet hat, dann erkennt man einen Zusammenhang zwischen dem Winkel und seiner gegenüberliegenden Seite: je größer der Winkel, desto länger ist die gegenüberliegende Dreiecksseite. Der Zusammenhang zwischen Winkel und seiner gegenüberliegenden Seite ist eine Funktion (im hier verwendeten Sinne eine mathematische Rechenvorschrift). Aus historischen Gründen werden die Winkelfunktionen am rechtwinkligen Dreieck abgeleitet. Im rechtwinkligen Dreieck heißt die dem rechten Winkel gegenüberliegende Seite Hypotenuse, die beiden anderen Seiten sind die Katheten. Hier unterscheidet man die Ankathete (b ist Ankathete zum Winkel α) und Gegenkathete (a ist Gegenkathete zum Winkel α).
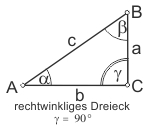
Da die drei Winkel im Dreieck zusammen 180° haben, muss der rechte Winkel (90°) der größte sein, und die Hypotenuse die längste Seite im rechtwinkligen Dreieck. Setzt man die Länge dieser Hypotenuse gleich 1, sind die Funktionen spitzer Winkel (< 90°) positive Zahlen, und der Sinus und der Cosinus sind immer kleiner als 1.
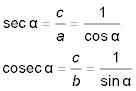
In alten Büchern findet man noch zwei weitere Winkelfunktionen: Secans (sec) und Cosecans (cosec). Es sind das die Kehrwerte von Sinus bzw. Cosinus.

Und zur Vereinfachung der Berechnungen im schiefwinkligen Dreieck gab es Tabellen des sinus versus (versin) und seiner halben Werte (Haversine). Die geometrische Erklärung wird im Zusammenhang mit den Sinustabellen gegeben.
(Anwendungsbeispiele gibt z. B. Snodgrass.)
Die Winkelfunktionen des gleichen Winkels stehen zu einander in Beziehungen. Man kann die leicht ableiten, wenn man den Satz des Pythagoras anwendet: a2 + b2 = c2. Setzt man für:
Da im rechtwinkligen Dreieck außerdem α + β = 90° gilt und die Phasenbeziehung der Winkelfunktionen sagt sin α = cos (90° - α), ist die Beziehung der Winkelfunktionen auch sin2 α + sin2 β = 1. Nach dem gleichen Formalismus erhält man:
Radiziert man diese letzte Formel erhält man:
Damit hat man eine einfache Beziehung für die Berechnung der Stücke des rechtwinkligen Dreiecks mit einem Rechenschieber, der eine "pythagoreische" Skala mit Werten von √(1 - sin2 β) trägt. Solche Rechenschieber sind vom System Darmstadt.
Durch Division der Winkelfunktionen sin und cos erhält man zwei neue:
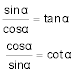
Mit diesen beiden Gleichungen kann man nun jede Funktion des Winkels α durch die anderen Funktionen ausdrücken:
| sin α | |||
| cos α | |||
| tan α | |||
| cot α | |||
Zwischen den Funktionen der Nebenwinkel (deren Summe ja 180° beträgt) gelten im rechtwinkligen Dreieck wegen β = 90° - α die Beziehungen:
Die Paare Sinus und Cosinus und Tangens und Cotangens werden jeweils Kofunktionen von einander genannt.
Jede Funktion eines spitzen Winkels ist gleich der Kofunktion seines Nebenwinkels.
Für die Benennung des Sinus gibt es zwei Erklärungen:
Die Winkelfunktionen geben die Länge einer Dreiecksseite in Abhängigkeit von Dreieckswinkeln an. Nun kann man am Rechenschieber leicht ablesen, welcher Winkel zu einer Seitenlänge gehört. Um aber mit Gleichungen rechnen zu können (z. B. auf dem Computer), benötigt man eine Funktion, die den Winkel aus einer Seitenlänge berechnet. Diese Funktionen nennt man Umkehrfunktionen der Winkelfunktionen. Sie heissen Arcussinus (arcsin), Arcuscosinus (arccos), Arcustangens (arctan) und Arcuscotangens (arccot; wird häufig nicht von Softwareprogrammen angeboten, da cot = 1 ⁄ tan). Softwareprogramme rechnen intern im Bogenmaß, sodass das Ergebnis der Umkehrfunktionen in Bruchteilen des Umkreisumfangs angegeben wird. Zur Umrechnung in das Winkelmaß wird diese Zahl mit 360° ⁄ 2 · π multipliziert.
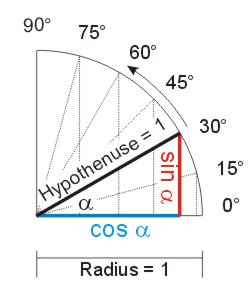
Zur Ableitung der Winkelfunktionen verwendet man einen Kreis mit Einheitsradius r = 1, in dem ein Strahl vom Mittelpunkt (im Gegenuhrzeigersinn) umläuft. Der Einfachheit halber wird nur ein Viertel des Kreises (Quadrant) abgebildet.
In einem Kreis mit dem Radius 1 (der Radius ist die Hypotenuse eines Dreicks) entspricht die Länge des Lotes (= Gegenkathete) dem Wert des Sinus, die Ankathete dem Wert des Cosinus.
Der Wert des Sinus beträgt 0 bei α = 0° und er beträgt 1 bei α = 90°; Der Cosinus ist 1 bei α = 0 und er ist 0 bei α = 90°. Wie man diese Zahlen berechnet, steht hier.
Eine Animation des Zusammenhangs gibt es hier.
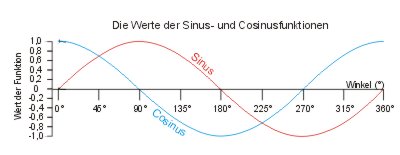
Läßt man den Hypotenusenstrahl über den ganzen Kreisbogen streichen und trägt die Längen sin α und cos α gegen den Winkel α, dann erhält man zwei Kurven, die zwischen 0 und 1 oszillieren. Man sagt, die Funktionen sind zyklisch.
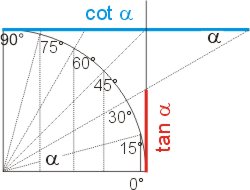
Um die Abhängigkeit des Tangens (und Cotangens) grafisch darzustellen, müssen der Hypotenusenstrahl über den Kreisbogen hinaus verlängert werden und zwei Tangenten des Umkreises eingezeichnet werden. Die Haupttangente steht senkrecht auf der Ankathete, die Nebentangente ist parallel zu ihr. Der Wert des Tangens entspricht dann der Strecke auf der Hauptkathete von der verlängerten Ankathete bis zum Schnittpunkt mit der verlängerten Hypotenuse. Man sieht, dass der Tangens für α = 0° Null ist und für α = 90° unendlich groß.
Der Cotangens entspricht in diesem Bild der Strecke auf der Nebenkathete vom Berührungspunkt mit dem Kreis bis zum Schnittpunkt der verlängerten Hypotenuse. Der Cotangens nimmt Werte zwischen 0 (bei α = 90°) bis unendlich (bei α = 0°) an. Diese beiden Funktionen sind nichtzyklisch.
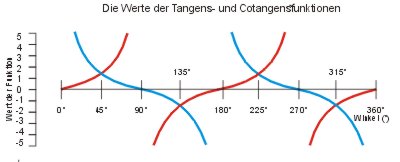
Für Winkel 0 < α < 360° sieht das Diagramm wie folgt aus. Ab bestimmten Werten für α werden die Werte für Tangens und Cotangens zu groß, um sie darzustellen. Die Tangensfunktion nimmt vor α < 90° und α < 270° unendlich große Werte an, und danach unendlich kleine; bei α = 90° und α = 270° ist sie unbestimmt. Deshalb sind die Tangensskalen auf dem Rechenschieber begrenzt auf Winkel 5,5° > α < 85,5°.
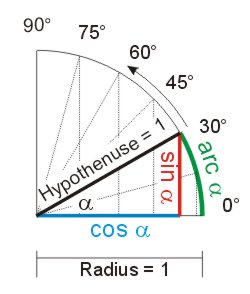
Für das Rechnen mit dem Rechenschieber muss noch eine weitere Winkelfunktion erklärt werden. Die Skalen des Rechenschiebers beginnen für den Sinus und Tangens mit 5,5°, nicht mit 0°. Für Winkel unter 5,5° benutzt man statt der Länge der Sehne die Länge des Kreisbogens (Arcus). Der Fehler ist wegen der eingeschränkten Genauigkeit des Rechenschiebers vernachlässigbar.
Die Tabellen der Funktionswerte des Sinus waren von höchster Bedeutung für die Astronomie und die Entwicklung der Weltbilder. Es wurde viel Aufwand in ihre Verbesserung und Genauigkeit gesteckt. Mit den Tabellen des Regiomontanus erreichte die Genauigkeit um 1475 ihren Höhepunkt bei ½°.
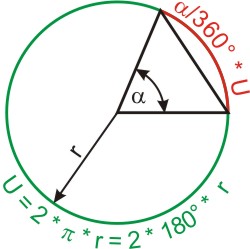
Zu erwähnen ist noch, dass man Winkel statt in Grad auch in Bruchteilen des Vollkreises angeben kann. Dabei wird der Vollkreis mit 360° gleich 2π gesetzt (π ist ja mit dem Umfang durch die Umfangformel definiert: U = 2· π · r, wobei r der Radius (halber Durchmesser) des Kreises ist. Dieses Winkelmaß nennt man Bogenmaß.
arc α = 2 · π · (α ⁄ 360°)
Eine Anwendung sind Entfernungsangaben in Seemeilen. Der Erdumfang ist 360° · 60′ = 21.600 Bogenminuten oder Seemeilen. Wenn man am Äquator — oder auf einem anderen Großkreis — eine Strecke von 15° fährt, so sind das 15°/360° · 21.600 sm = 900 sm.
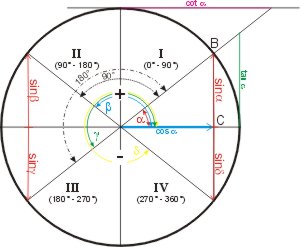
Die Größen der Winkelfunktionen wurden im Bereich α = 0° - 90° (1. Quadrant des Vollkreises) diskutiert. Betrachte wir die Größe der Winkelfunktionen im Bereich 0° bis 360° (Vollkreis). Wir erkennen:
erhalten wir die Beziehungen:
Für die anderen Winkelfunktionen kann man analoge Beziehungen ablesen. Es ergibt sich die Phasenbeziehungen der Winkelfunktionen.
| sin α | cos α | tan α | cot α | ||
| -α | -sin α | cos α | -tan α | -cot α | Umklappungssatz |
| 90° ± α | cos α | +sin α | +cot α | +tan α | Drehungssätze |
| 180° ± α | +sin α | -cos α | ±tan α | ±cot α | |
| 270° ±α | -cos α | ±sin α | +cot α | +tan α | |
| 360° ± α | ±sin α | cos α | ±tan α | ±cot α | |
Schließlich benötigt man zum Rechnen mit Winkelfunktionen noch die Ausdrücke für zusammengesetzte Winkel und für Summe und Differenz von Winkelfunktionen.
| Additionstheoreme | Summen der Winkelfunktionen |
sin (α ± β) = sin α · cos β ± cos α · sin β
cos (α ± β) = cos α · cos β ∓ sin α · sin β
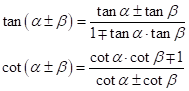
|
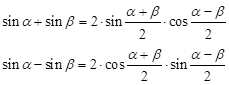
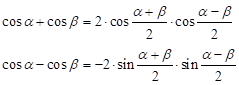
|
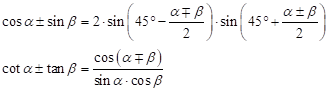
|
|
Zum eleganten Umformen von Gleichungen gibt es noch die Formeln für die trigonometrischen Funktionen der doppelten und der halben Winkel.
| doppelte Argumente | halbe Argumente |
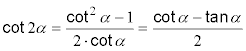 |
|
Aus den Additionstheoremen (s. o.) läßt sich noch ein interessantes Konzept zur Multiplikation von Winkelfunktionen durch Addition (gr. prosthesis) und Subtraktion (gr. apharesis) von Winkeln ableiten. Es soll von Johannes Werner aus Nürnberg im Jahre 1510 (nach anderen Quellen von Ibn Junis im 11. Jahrhundert) entdeckt worden sein. Damit wurden die Multiplikationen von Winkelfunktionen in den Formeln der sphärischen Trigonometrie etwas einfacher. Tycho Brahe jedenfalls propagierte diese Methode.
Die praktische Arbeit mit der Prosthapharese macht sich die Zusammenhänge zu nutze:
Mit Hilfe von Sinus-Tabellen konnte man so auch Zahlen multiplizieren: man suchte die zu den Zahlen gehörenden Winkel in der Tabelle. Deutlich einfacher wurden die Berechnungen erst durch die Erfindung der Logarithmen durch Johann Napier, Henry Briggs und Jos Bürgi und deren Logarithmentabellen.
© Dr. Rainer Stumpe, URL: https://www.rainerstumpe.de