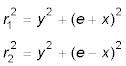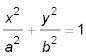Die Mittelpunktsgleichung Ellipse
Karthesische Koordinaten
Die Ellipse wird definiert als die Kurve, auf der für alle Punkte P(x,y) die Summe der Abstände zu den beiden Brennpunkten F1,2 konstant ist PF1 + PF2 = r1 + r2 = konstant. Diese Konstante ist das zweifache der großen Halbachse a: r1 + r2 = 2 · a.
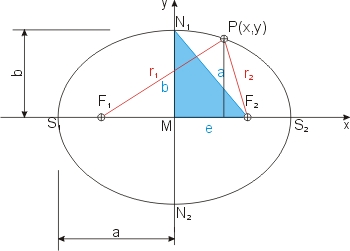 Mit dem Lot von P auf die x-Achse erzeugen wir zwei rechtwinklige Dreiecke, die r1 bzw. r2 als
Hypotenuse haben, und eine Kathete gemeinsam haben (deren Länge ist y). Wir können den Satz des Pythagoras anwenden und erhalten:
Mit dem Lot von P auf die x-Achse erzeugen wir zwei rechtwinklige Dreiecke, die r1 bzw. r2 als
Hypotenuse haben, und eine Kathete gemeinsam haben (deren Länge ist y). Wir können den Satz des Pythagoras anwenden und erhalten:
Mit der Definition der Ellipse (r1 + r2 = 2·a) erhalten wir durch Umformen und Einsetzen die Mittelpunktsgleichung der Ellipse:
Mit dieser Gleichung können wir nun die Koordinate x oder y eines Punktes P(x,y) aus der jeweils anderen berechnen, der auf der Ellipse mit den Halbachsen a und b liegt.
Polarkoordinaten
Polarkoordinaten beschreiben die Lage eines Punktes durch den Abstand ρ vom Koordinatennullpunkt und den Winkel φ, den dieser vom Mittelpunkt ausgehende Strahl mit der x-Achse einschließt. Auf der Ellipse muß man nun einen Ausdruck für den Abstand ρ und den Winkel φ finden.
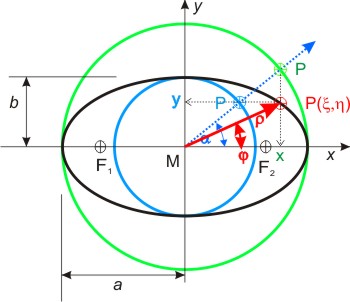 Die Ellipse kann man als gestauchten Kreis ansehen; alle y-Koordinaten der Punkte auf einer Ellipse sind im Verhältnis y : η = b : a verkürzt. Läßt man einen Strahl von Mittelpunkt der Ellipse um den Winkel α laufen, dann kann man die Koordinaten eines Punktes P(ξ,η) auf der Ellipse durch die Koordinaten von Schnittpunkten auf den Inkreis (blau) und dem Umkreis (grün) ausdrücken. Die y-Koordinate η ist identisch mit der y-Koordinate des Punktes auf dem Inkreis (Radius b): η = y = b · sin α.
Die Ellipse kann man als gestauchten Kreis ansehen; alle y-Koordinaten der Punkte auf einer Ellipse sind im Verhältnis y : η = b : a verkürzt. Läßt man einen Strahl von Mittelpunkt der Ellipse um den Winkel α laufen, dann kann man die Koordinaten eines Punktes P(ξ,η) auf der Ellipse durch die Koordinaten von Schnittpunkten auf den Inkreis (blau) und dem Umkreis (grün) ausdrücken. Die y-Koordinate η ist identisch mit der y-Koordinate des Punktes auf dem Inkreis (Radius b): η = y = b · sin α.
Die x-Koordinate des Punktes P(ξ,η) auf der Ellipse ist gleich der x-Koordinate des Punktes auf dem Umkreis (Radius a). Damit lauten die Transformationsgleichungen:
- x = ξ = a · cos α
- y = η = b · sin α
Mit dem Pythagoras erhält man für den Abstand ρ des Ellipsenpunktes vom Mittelpunkt den Ausdruck:
- ρ2 = a2·cos2α + b2·sin2α
Nun brauchen wir noch eine Beziehung zwischen dem Winkel α in dieser Gleichung und dem Polarkoordinatenwinkel φ. Der ist gegeben durch die Definition tan φ = η/ξ = b·sin α / a·cos α. Durch Umformen und Einsetzen bekommt man schließlich die Polargleichung der Ellipse ( mit ε numerische und e lineare Exzentrizität):
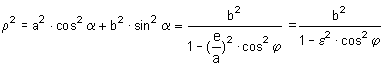
Diese Gleichung beschreibt ebenfalls die Ellipse, nur sind die Koordinaten eines Punktes auf ihr durch den Abstand ρ vom Mittelpunkt und den Winkel φ zwischen ρ und der x-Achse angegeben.
Umfang der Ellipse
Diese polare Mittelpunktsgleichung hat den Vorteil, dass man sie differenzieren kann (zum Formalismus s. a. Loxodrome). Integriert man dann das Differenzial, erhält man entweder die Länge des Ellipsenbogens, oder die Fläche über der Winkeländerung.
Bei der (terrestrischen) Navigation interessiert ausschließlich die Länge des Bogens (also die Entfernung zwischen den Punkten P1(ρ1,α1) und P2(ρ2,α2), die der Winkeländerung Δα entspricht. Dieses Integral hat die Form:
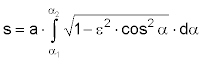
Es ist allerdings nicht analytisch zu lösen (ausser in den Grenzen zwischen 0° und 90°, also für den Viertelbogen). Man muß den Wurzelausdruck in eine konvergierende Reihe entwickeln, und deren Glieder einzeln integrieren. So erhält man für die Bogenlänge der Ellipse die Formel:
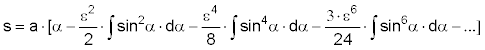
Man sieht, das ist recht aufwändig zu berechnen. Zudem macht man einen Fehler, wenn man die Reihe nach einer endlichen Zahl Glieder abbricht. Integriert man diese Gleichung von 0° bis 360°, erhält man den Umfang der Ellipse.
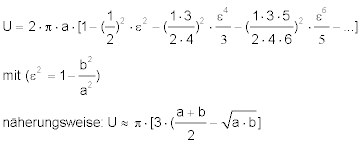
Wie groß ist der Fehler? Berechnen wir die Reihenglieder für den Polumfang des WGS84 Ellipsoids.
| große Halbachse | a = 6.378.137,0 m | a2 = 40.680.631.590.769,0000 |
| kleine Halbachse | b = 6.356.752,3143 m | b2 = 40.408.299.985.358,4000 |
| numerische Exzentrizität | ε = 0,081819190738 | ε2 = 0,006694379973 |
| 1. Glied = 0,001673594993 | 2. Glied = 0,000002100690 | 3. Glied = 0,000000005860 | |
| Umfang | 40.007.947,3383 | 40.007.863,1531 | 40.007.862,9183 |
| Beitrag | 84,1852 | 0,2348 | |
| Näherungsformel | 40.007.862,9174 | ||
| Kreis mit Radius b | 39.940.652,7426 | ||
Wir erkennen, dass das zweite Glied eine Korrektur des Polumfangs von etwa 100 m, das dritte eine von 20 cm beiträgt. Zum Vergleich ergibt die Näherungsformel einen Polumfang, der etwa dem des Reihenabbruchs nach dem ersten Glied entspricht. Der Umfang eines Kreises mit Radius der kleinen Halbachse ist etwa 70 km kürzer als der Ellipsoidumfang (ist ja auch noch ganz ordentlich!).
Ich vermute, das (zivile) GPS arbeitet mit der Näherungsformel, und hat deshalb einen Fehler von (mindestens) 100 m. Das differentielle GPS (DGPS) erlaubt eine weitgehende Korrektur; entsprechend ausgerüstete Geräte haben wohl auch leistungsfähigere Rechner, die bis zum zweiten oder dritten Glied der Reihe rechnen, und so auf Fehler unter 1 m kommen können.
Die Fläche des Ellipsensektors
Etwas einfacher ist die Fläche des Ellipsensektors zu berechnen. da wir es an anderer Stelle brauchen, soll hier nach dem gleichen Formalismus auch die Fläche des Kreissegmentes berechnet werden.
 Die Fläche des blauen Sektors des Kreises soll berechnet werden. Die Funktion des Kreises lautet:
Die Fläche des blauen Sektors des Kreises soll berechnet werden. Die Funktion des Kreises lautet:
 .
.
In differenzierter Form und nach Substitution von x = r · cos φ und dx = r · sin φ:

- (Zur Erinnerung: sin2 φ + cos2 φ = 1)
Integrieren mit den Grenzen φ = 0 bis φ ≤ 90° ergibt die Fläche F:
In den Grenzen φ = 0° bis φ = 90° = π ⁄ 2 erhalten wir für ¼ der Kreisfläche:
- F ⁄ 4 = (r2 ⁄ 2) · sin (π ⁄ 2) · cos (π ⁄ 2) + π ⁄ 2 = (r2 ⁄ 2) · (π ⁄ 2);
- F = π · r2.
Die Fläche des gelben Ellipsensektors erhalten wir analog aus der Funktion der Ellipse:
Integrieren mit den Grenzen φ=0 bis φ≤90° ergibt die Fläche F:
Die Scheitelgleichung der Ellipse
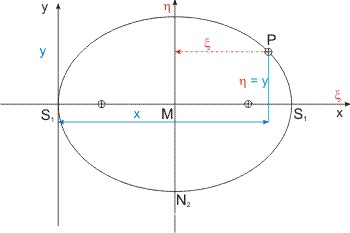 Verlegt man den Ursprung des karthesischen Koordinatensystems vom Mittelpunkt M der Ellipse in einen der Hauptscheitel S1, 2, kann man die "Scheitelgleichung" der Ellipse ableiten. Die Kegelschnitte lassen sich über ihre Scheitelgleichungen vergleichen. Zur Ableitung verwenden wir eine Translation des Ursprungs im Mittelpunktsystem M(ξ η) in das Scheitelsytem S(x, y). Die y-Koordinate ist gleich der η-Koordinate, die ξ-Koordinate wird zu x-Koordinate durch Addition der Strecke MS1 = a (große Halbachse).
Verlegt man den Ursprung des karthesischen Koordinatensystems vom Mittelpunkt M der Ellipse in einen der Hauptscheitel S1, 2, kann man die "Scheitelgleichung" der Ellipse ableiten. Die Kegelschnitte lassen sich über ihre Scheitelgleichungen vergleichen. Zur Ableitung verwenden wir eine Translation des Ursprungs im Mittelpunktsystem M(ξ η) in das Scheitelsytem S(x, y). Die y-Koordinate ist gleich der η-Koordinate, die ξ-Koordinate wird zu x-Koordinate durch Addition der Strecke MS1 = a (große Halbachse).
Aus der Mittelpunktsgleichung oben wird, mit den Koordinaten ξ und η:
![]() durch Einsetzen von ξ = x - a und η = y:
durch Einsetzen von ξ = x - a und η = y:
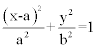 .
.
Nach Auflösen der Gleichung nach y² erhält man:
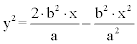 .
.
Jetzt erinnert man sich an den Ellipsenparameter p: p = b² ⁄ a, substituiert ihn in der Formel und erhält: y² = 2·p·x - p·x² ⁄ a, die Scheitelgleichung der Ellipse.
- Stichworte zu Kegelschnitten und Ellipse:
- Die Geometrie der Ellipse
- Die lineare Exzentizität
- Die numerische Exzentizität
- Ellipse und Umkreis
- Mittelpunktsgleichung der Ellipse
- Polare Mittelpunktsgleichung der Ellipse
- Umfang der Ellipse
- Fläche des Ellipsensektors
- Scheitelgleichung der Ellipse
- Brennpunktgleichung der Ellipse
- Kegelschnitte
- Die Kepler-Gleichung
|
|
© Rainer Stumpe URL: http://www.rainerstumpe.de |