Die Brennpunktsgleichung der Ellipse

In der Schule lernte man zu meiner Zeit außer der Mittelpunktsgleichung noch die Scheitelgleichung der Ellipse. Viel interessanter ist die Brennpunktsgleichung: sie ist die Schlüsselformel für die Vorhersage von Sternenorten. Der Grund hierfür sind das 1. und 2. Keplersche Gesetz: die Erde bewegt sich auf einer El­lip­sen­bahn um die Sonne, die in einem der beiden Brennpunkte der Bahnellipse steht. Das zweite Kep­ler­sche Gesetz ist in der Kepler-Gleichung bereits enthalten. Leider ist die Brennpunktgleichung der Ellipse von Kepler transzendent, d. h. man kann mit ihr nicht rechnen.

Polarkoordinaten

Hier braucht man die Polargleichung, die als Ursprung den Brennpunkt hat. Die Brennpunktsgleichung in kathesischen Koordinaten ist offensichtlich ungebräuchlich (— jedenfalls habe ich nur einen Hinweis bei Carl Friedrich Gauss gefunden). Die Ableitung erfolgt ähnlich wie bei der Mittelpunktgleichung.

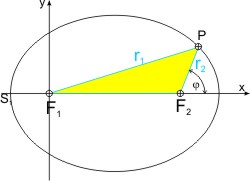Zum Unterschied ist jedoch das gelbe Dreieck ΔF₁F₂P schiefwinklig, und wir müssen den Cosinussatz anwenden:

r₁² = (2 · r₂)² + (2 · e)² - 2 · 2 · e · r₂ · cos (180° - φ)

Ausmultiplizieren und Auflösen nach r₂ liefert:

Teilt man die rechte Seite durch a, erhält man mit e²/a = ε:

In der Form ähnelt diese Brennpunktgleichung der Mittelpunktgleichung.

Diese polare Brennpunktsgleichung der Ellipse könnte man nun wieder differenzieren und integrieren. Aber die Hauptanwendung ist die Bestimmung des Ortes der Erde auf ihrer Umlaufbahn um die Sonne in Abhängigkeit von der Zeit. Dieses Problem hatte schon Johannes Kepler, und er hat eine Lösung gefunden — ohne Differenzialrechnung (die war noch nicht erfunden, das haben erst 50 Jahre später von Newton und Leibnitz entwickelt). Keplers Methode ist hier erklärt.

Kathesische Koordinaten

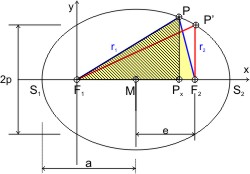Um die Brennpunktgleichung in karthesischen Koor­di­naten zu entwickeln, wählt man einen der Brenn­punkte als Ursprung des Koordinatensytems. In dem gelben Dreieck ΔF₁F₂P sind bekannt:

• die Summe der blauen Fahrstrahlen r₁ und r₂ aus der Definition der Ellipse: r₁ + r₂ = 2·a (a ist die große Halb­achse der Ellipse),
• und
• die Länge der Seite F₁F₂ = 2 · e (e ist die lineare Exzentrizität).

Der Umfang U des Dreiecks ΔF₁F₂P ist also konstant für alle Punkte P_{x, y} auf der Ellipse: U = r₁ + r₂ + 2 · e.

Für den Fall P′_x = 2 · e, so ist P′_y = p, der Ellipsenparameter. Der Ausdruck für den konstanten Umfang U ergibt sich in diesem Fall zu: U = r₁ + p + 2 · e. Und da in diesem Sonderfall das Dreieck ΔF₁F₂P′ rechtwinklig ist, kann man die Länge von r₁ angeben: r₁² = p² + 4 · e².

Da U eine Konstante für alle Punkte P_{x, y} ist, und nur von den beiden Ellipsenhalbachsen a und b abhängt, kann man mit dem rechtwinkligen, schraffierten Dreieck ΔF₁P_xP mit der Beziehung zwischen der Hypotenuse r₂ und den Katheten eine Gleichung aufstellen, die die Länge des Fahrstrahls r₁ mit der y-Koordinate des Punktes P korreliert (ist allerdings etwas aufwändiger).

• Eine Formel der Ellipse in karthesischen Koordinaten mit dem Ursprung in einem der Brenn­punkte ist nur in der Form der Kepler-Gleichung möglich! — und die ist transzendent und daher nicht analytisch auflösbar.

In der Ableitung der Kepler-Gleichung gibt es eine Formel, die die Länge des Fahrstrahls r₁ mit dem Winkel φ dieses Strahls und der Ellipsenhauptachse in Verbindung bringt.

Dabei sind a und b die große bzw. die kleine Hauptachsen der Ellipse, ε ist die numerische Exzentizität. Aus dieser Formel kann man den Winkel φ berechnen, und mit der Definition des Sinus und der Länge des Fahrstrahls r erhält man die y-Koordinate des Ellipsenpunktes.

• Stichworte zu Kegelschnitten und Ellipse:
• Die Geometrie der Ellipse
• Die lineare Exzentizität
• Die numerische Exzentizität
• Ellipse und Umkreis
• Mittelpunktsgleichung der Ellipse
• Polare Mittelpunktsgleichung der Ellipse
• Umfang der Ellipse
• Fläche des Ellipsensektors
• Scheitelgleichung der Ellipse
• Brennpunktgleichung der Ellipse
• Kegelschnitte
• Die Kepler-Gleichung