Die Kegelschnitte

Geschichtliches

Die Griechen beschäftigten sich um 500 v. Chr. intensiv mit Konstruktionsaufgaben. Zu den Kegel­schnit­ten arbeiteten Euklid (vier Bücher), Apollonius (8 Bücher auf der Basis Euklids) und Aristaios (zu spitz­wink­ligen, rechwinkligen und stumpfwinkligen Kegeln). Bei Euklid waren es rechtwinklige Kegel, die ent­ste­hen, wenn man ein rechtwinkliges Dreieck um eine der Kathethen dreht.

Die Kegelspitze kann man abschneiden und erhält dann einen Kegelstumpf. Apollonius untersuchte die Schnittlinien mit dem Kegelmantel für unterschiedliche Schnittwinkel und fand die Parabel, die Ellipse und die Hyperbel — je nach der Neigung der schneidenden Ebene.

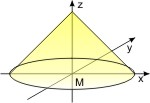Kegel Der gerade Kreiskegel hat als Grundfläche einen Kreis, und die Verbin­dungs­linie der Kegelspitze mit dem Mittelpunkt der Grundfläche (Kegel­höhe) steht senkrecht auf der Basis. Seine Mantelfläche wird be­schrie­ben durch die Formel: a · x2 + b · y2 = c ·z2. Beim Einheitskegel ist a = b = c = 1.

In der analytischen Geometrie wird eine Ebene durch die Formel a · x + b ·y + c · z = d. (a, b, c, d sind Konstanten.) Alle Punkte für die so­wohl die Kegelgleichung wie die Ebenengleichung erfüllt sind, ergeben den Schnitt der beiden.

Die Ellipse

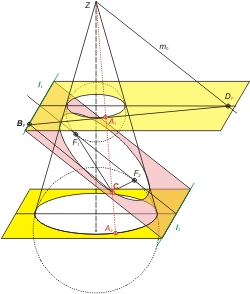ellipse Die Form der Kegelschnitte hängt außerdem vom Win­kel β ab, den die Man­tel­linie des Kegels mit der Ho­ri­zon­talen einschließt. Als Maß führt man die nu­me­rische Ex­zen­tri­zi­tät ε ein. Sie ist das Verhältnis des Sinuswerte der Winkel α und β: ε =  sin α ⁄ sin β. Im Falle der Ellipse ist der Win­kel α kleiner ist als der Winkel β. Dann ist auch sin α klei­ner als sin β, und der Quotient ε ist kleiner als 1.

In der Abbildung sind auch die beiden Dandelinschen Kugeln eingezeichnet. Sie werden dem Kegel so ein­ge­schrie­ben, dass sie die Ellipse in den Brennpunkten be­rüh­ren (rote Punkte). Die Ebenen, in denen die Kugeln den Kegelmantel berühren (hier gelb), parallel zur Grund­fläche des Kegels, schneiden sich mit der Ebene, die die Ellipse aus der Kegelhülle aus­schnei­det (hier rot), in den Leitlinien (grün, strichpunktiert). Die Ei­gen­schaf­ten der Ellipse sind an anderer Stelle aus­führ­lich erklärt; dort werden auch abgeleitet:

Die Parabel

Parabel 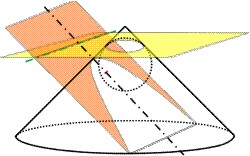Um eine Parabel zu erzeugen, muß die den Kegel schnei­dende Ebe­ne parallel zur Hülle des Kegels liegen. Es ist also α = β oder ε = 1. Die beiden Äste der Parabel schnei­den sich nie und verlaufen erst im Unendlichen parallel zu ein­an­der.
Bei der Parabel gibt es nur einen Berührungspunkt der Dandelin­schen Kugel, der als Brennpunkt der Parabel bezeichnet wird, und eine Leitlinie, die sich wie bei Ellipse und Hyperbel ergibt. Die Leitlinie hat vom ein­zi­gen Brenn­punkt den Abstand p, den Parameter der Parabel (die Seh­ne senkrecht zur Achse der Parabel durch den Brenn­punkt hat die Länge 2 · p).

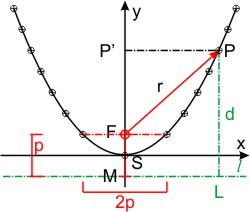Parabel Die Parabel hat nur einen Brenn­punkt, der andere liegt im "unendlichen". Sie ist symmetrisch zur ihrer (y-) Achse, und zu jedem Punkt P(x,y) auf einem der Zweige gibt es daher einen zweiten P(-x,y), dessen Koordinaten sich nur im Vor­zei­chen der x-Koordinate unterscheiden.

Jeder Punkt P auf der Parabel hat vom Brennpunkt F den gleichen Abstand r wie von der Leitlinie l: r = d. Im Ko­or­di­na­ten­system mit dem Scheitel S der Parabel im Ur­sprung hat der Brennpunkt F den Abstand FS = p ⁄ 2. Die Länge des Fahrstrahls zum Punkt P(x,y) errechnet man nach Pythagoras im Dreieck FPP′:

  • r² = (y - p ⁄ 2)² + x²,
  • also
  • r = √[(y - p ⁄ 2)² + x²].

Der Abstand d des Punktes P von der Leitlinie l ist: d = y+ p ⁄ 2.

Wegen der Bedingung für die Parabel (r = d) ist damit r² = (y - p ⁄ 2)² + x² = d² = (y + p ⁄ 2)². Ausmultiplizieren ergibt:

  • y² - 2 · p ⁄ 2 · y + (p ⁄ 2)² + x² = y² + 2 · p ⁄ 2 · y + (p ⁄ 2)²
  • und kürzen und auflösen nach x² führt schließlich zur Scheitelgleichung der Parabel:
  • x² = 2·p · y.

Natürlich gibt es auch noch andere Formeln für die Parabel — analog zur Ellipse — die findet man aber auch an anderer Stelle im Web abgeleitet.

Die Hyperbel

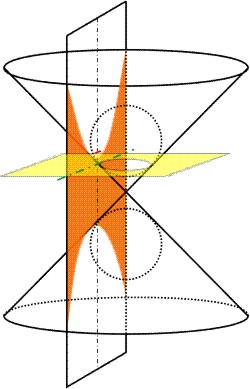Hyperbel Schneidet die erzeugende Ebene parallel zur Kegelachse den Doppelkegel, so entsteht eine Hyperbel. Eine hy­per­bel­er­zeu­gen­de Schnittebene muß schneidet beide Teile des Doppelkegels. Deshalb hat sie zwei Äste, und ist sym­me­trisch zur Verbindunglinie der beiden Scheitel S1,2 und auch zur Senkrechten im Mittelpunkt M (wie übrigens auch die Ellipse).

Auch hier gibt es zwei Dandelinschen Kugeln, die die schneidende Ebene in den Brennpunkten der Hyperbel be­rüh­ren, und die Schnittlinie der Ebenen durch die Be­rüh­rungs­kreise der Dandelinschen Kugeln mit der er­zeu­gen­den Ebene sind die Leitlinien der Hyperbel.

Die Hyperbel wird beschrieben durch die Linien auf dem Kegelmantel, die die Schnittebene mit dem Mantel ge­mein­sam habeb. Es sind dies die Asymptoten, denen sich die Äste der Hyperbel "asymptotisch" annähern. Die A­symp­toten schnei­den sich im Mittelpunkt M der Hy­per­bel. Sie schließen den Winkel 2 · α ein, den Öff­nungs­winkel an der Kegelspitze.

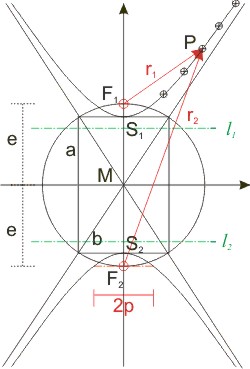Hyperbel Die beiden Scheitel haben den Abstand a (bei der El­lip­se die große Halbachse, die kleine gibt es bei der Hy­per­bel nicht, sie ist aber die kürzere Seite im Recht­eck aus den Schnittpunkten eines Kreises mit dem Radius der linearen Exzentrizität e mit den Asymp­to­ten). Dieser Kreis schneidet die Achse durch die Scheitel in den bei­den Brennpunkten F1 und F2 (deren Abstand vom Mit­tel­punkt M ist die lineare Exzentrizität e — wie bei der Ellipse). Während bei der Ellipse die Summe der beiden Brennstrahlen konstant ist, ist es bei der Hyperbel die Differenz der Brennstrahlen r2 - r1 = 2 · a. Deshalb lautet die Mittelpunktsgleichung der Hyperbel: Mittelpunktsgleichung der Hyperbel.

Bei der Hyperbel gibt es zwei Leitlinien l1 und l2. Ihre Abstände von von den Scheiteln S1,2 ist y1,2 = ± a² ⁄ e. Der Scheitel S1 hat vom Mittelpunkt den Abstand a. Im Koordinatensystem mit dem Scheitel im Ursprung ergibt sich aus der Mittelpunktsgleichung für die y-Koordinate des Punktes P also mit 2 · p als Länge der Sehne durch den Brennpunkt:

Scheitelgleichung der Hyperbel

Vergleich der Scheitelgleichungen der Kegelschnitte

Die Scheitelgleichungen der Kegelschnitte werden in allen zeitgenössischen Quellen gegenübergestellt, weil mit ihnen die Bezeichnungen aus dem Griechischen ableiten lassen. Aber offensichtlich ist der Hin­ter­grund der griechischen Namensgebung in Vergessenheit geraten. (Im Grunde könnte man natürlich auch die Mittelpunktsgleichungen von Ellipse und Hyperbel vergleichen, allerdings hat die Parabel keinen Mit­tel­punkt.) Also will ich es weiter unten herleiten.

Parabel : y² = 2 · p · x
Ellipse : y² = 2 · p · x - p · x² ⁄ a
Hyperbel : y² = 2·p · x + p · x² ⁄ a
gemeinsame Scheitelgleichung : y² = 2 · p · x - (1 - ε²) · x²

Die Bedeutung der Scheitelgleichung und das "Gnomon"

Die Scheitelgleichungen der Kegelschnitte werden in aktuelleren Quellen etwas düftig behandelt. (Für Prob­lem­lösungen seit Kepler seine Gleichung veröffentlichte, sind auch die Mittelpunkts- und vorallem die Brennpunktsgleichung interessanter.) Man muß schon ein wenig zurück gehen, um die Bedeutung der Schei­tel­gleichung zu finden — bis zu Euklid. In Keplers Liber Quintus gibt es eine hübsche Anwendung für das Gnomon.

Unter anderen interpretiert Prof. Dörte Haftendorn, Uni Lüneburg, die Namensgebung Parabel (παραβαλλειν: paraballein, gleichkommen), Hyperbel (μπερβαλλειν: hyperballein, übersteigen) und Ellipse (ελλειπειν: elleipein, ermangeln) mit dem gemeinsamen Glied 2 · p · x, das bei der Parabel fehlt, bei der Hy­per­bel um (p ⁄ a) · x² vergrößert und bei der Ellipse verringert wird.

Helmuth Gericke3 weist auf die Lösung quadratischer Gleichungen durch geometrische Konstruktion der griechischen Mathematiker mit dem "Gnomon" hin. Da Kepler diese Rechenmethode im Kapitel III (De figura orbita) des Liber Quintus anwendet soll sie kurz erläutert werden.

Gericke bezieht sich in seinem Buch3 auf Euklids Lehrsatz 5 im 2. Buch:

Teilt man eine Strecke sowohl in gleiche als auch in ungleiche Abschitte, so ist das Recht­eck aus den ungleichen Abschnitten der ganzen Strecke zusammen mit dem Quad­rat über der Strecke zwischen den Teilpunkten dem Quadrat über der Hälfte gleich.

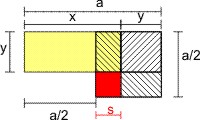Gnomon Das Bild stellt den Lehrsatz Euklids dar. Nun soll die Fläche des gelben Rechtecks plus die des roten kleinen Quadrats unten links gleich der Fläche des schraffierten Quadrats sein. Die Recht­eck­fläche ist x·y, die des großen Quadrats (a ⁄ 2)² = (x + y)². Das kleine Quadrat hat die Fläche

  • ((a ⁄ 2) - y)² = ((x - y) ⁄ 2)².
  • Also:
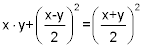
  • Gnomon

In geometrischen Größen ausgedrückt: die Fläche des nicht-schraffierten Teil des gelben Recht­ecks ist gleich der daneben liegenden schraffierten Fläche, und die beiden schraffierten Rechtecke sind gleich groß. Also erhält man die Fläche des gelben Rechtecks als Differenz des großen Quadrats und des kleinen roten Quadrats. (Die schraffierte, L-förmige Fläche nennt Euklid ein Gnomon.)

Damit hat man zwei Strecken gefunden, deren Summe x + y = a ist, und deren Produkt die Fläche c² ist. Die Gleichung dazu ist x · (a - x) = c². Die kann man umformen: x² - a · x = c². Das entspricht der Form nach der Scheitelgleichung der Ellipse, wo a = 2 · p.

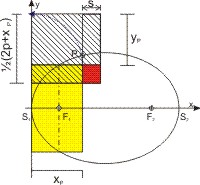Gnomon Mit dieser Gnomonkonstruktion kann man z. B. die y-Koordinate eines Ellipsenpunktes für eine beliebige x-Koordinate konstruieren. Man konstuiert das Gnomon der Fläche des Rechtecks aus dem Ellipsenparameter 2·p und der x-Koordinate des Punktes P, xP, und findet die y-Koordinate yP. Auf der y-Achse wird die Strecke 2 · p um xP verlängert, und die resultierende Strecke halbiert. Auf ihr errichtet man das Quadrat. Die Gnomonfläche (schraffiert plus das rote Quadrat) ist FG = [(2 · p + xP) ⁄ 2]² - yP². Sie ist gleich der gelben Rechteckfläche 2 · p·xP plus dem roten Quadrat.

Das Gnomon bei Hyperbel und Parabel

Ähnliche Konstruktionen gibt es auch für die Koordinaten eines Punktes auf der Parabel bzw. auf der Hy­per­bel. Eine ausführliche Darstellung der Euclidis Elementa findet man von David E. Joyce4.

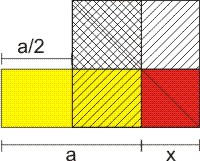Gnomon Das Gnomon eines Hyperbelpunktes (rechts oben nach links unten schraffiert) konstruiert man aus dem gelben Rechteck mit Kan­ten­länge a über ein Hilfsquadrat mit der Seitenlänge a ⁄ 2 (links oben nach rechts unten schraffiert) das rote Quadrat.

Die Anleitung findet man bei Euclids Elementa im Buch 2, Lehr­satz 5. Es löst die Gleichung x² - b·x = C, also die Schei­tel­gleichung der Hyperbel.

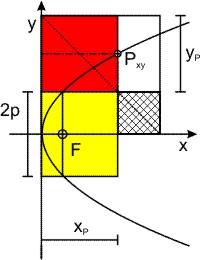Gnomon Um die y-Koordinate des Punktes Px,y auf einem Ast der Hyperbel zu erhalten, zeichnet man ein Rechteck (hier gelb) mit den Seiten 2·p und yP, das man ein Quadrat mit der Seitenlänge p anschließt (hier schraffiert). Die Diagonale des Quadrats verlängert man über die Ecke des Rechtecks bis zur y-Koordiante. Das rote Rechteck hat dann die Seiten xP und yP.

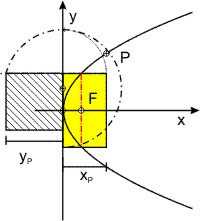Gnomon Einfacher ist die Konstruktion der y-Koordinate eines Pa­ra­bel­punk­tes Px,y, da man das gelbe Rechteck nur in ein Quadrat um­zu­wan­deln hat.

Man zeichnet wieder ein Rechteck mit den Seiten 2 · p und xP und verlängert die lange Seite um xP. Die Streckensumme aus 2 · p und xP wird halbiert und um den Halbierungspunkt wird ein Kreis mit dem Radius (2 · p + xP) ⁄ 2 geschlagen, der die Verlängerung der kürzeren Rechteckseite schneidet. Der Abstand des Schnittpunktes von der y-Koordinate ist die gesuchte Koordinate yP des Parabelpunktes.
Biograhische Notizen
Germinal Pierre Dandelin
Belgischer Mathematiker, geb. 12.04.1794 in LeBourget, gest. 15.02.1847 in Brüssel. Bewies dass die nach ihm benannten Kugeln einen Kegelschnitt in den Brennpunkten berühren. Offizier der Pioniere. Beschäftigte sich mit Geometrie. (Quelle: School of Mathematics and Statistics, University of St Andrews, Scotland)
Verwendete Quellen:
  1. Adolf Wildbrett: Analytische Geometrie, Bayerischer Schulbuch-Verlag, 1948.
  2. Mathematik-Ratgeber (Herausg. W. Gellert), VEB Bibliographisches Institut Leipzig, 1984.
  3. Helmuth Gericke, Mathematik in Antike und Orient, Springer-Verlag Heidelberg Berlin, 1984.
  4. David E. Joyce, Euclid's Elements, Math and Computer Science, Clark University, Worcester, MA, USA.
  5. Joh. Jos. Ign. Hoffmann: Die geometrischen Bücher der Elemente des Euclides; als Leitfaden zum Unterrichte in der Elementar-Geometrie, Mainz, 1829.
Valid HTML 4.01 © Rainer Stumpe URL: www.rainerstumpe.de