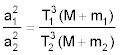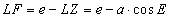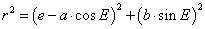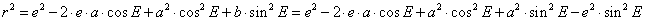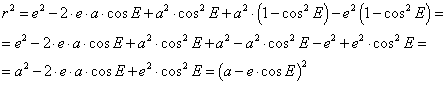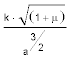Keplers Beitrag zu unserem Weltbid.
Die Keplerschen Gesetze.
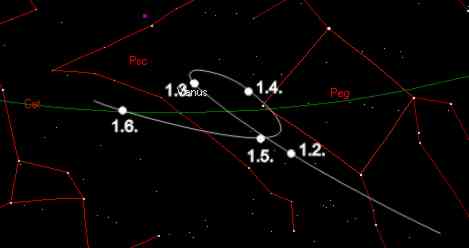
Zeichnet man die von der Erde aus beobachteten Bewegungen der inneren Planeten unseres Sonnensystems relativ zum Fixsternhimmel auf, so beobachtet man seltsame Schleifenbewegungen. Diese Schleifen waren mit der geozentrischen Theorie von Nikolaus Kopernikus nur sehr schwer zu erklären.
Johannes Kepler wertete die Planetenbeobachtungen seines Lehrers Tichio Brahe aus, und stellte fest, die Planetenbahnen lassen sich verstehen, wenn man annimmt, dass sie sich nicht auf Kreisen, sondern auf Ellipsen um die Sonne bewegen.
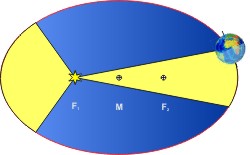
Eine Ellipse hat einen Mittelpunkt M und zwei Brennpunkte F1,2. Für jeden Punkt auf der Ellipse ist die Summe der Abstände zu den beiden Brennpunkten konstant. Die Ellipse wird beschrieben durch die große und die kleine Halbachsen (auf der großen Achse liegen der Mittelpunkt und die beiden Brennpunkte, die kleine steht senkrecht darauf und geht durch den Mittelpunkt), a und b, und die Exzentizizät e (das ist der Abstand jedes Brennpunktes zum Mittelpunkt).
- Keplersches Gesetz:
Die Planeten bewegen sich auf Ellipsen um die Sonne, die in einem der beiden Brennpunkte steht. - Keplersches Gesetz:
Die von der Sonne zum Planeten gezogenen Fahrstrahlen überstreichen in gleichen Zeiträumen gleiche Flächen. - Keplersches Gesetz:
Die Quadrate der Umlaufzeiten der Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen ihrer Bahnellipsen.
Das erste und das zweite Gesetz gelten exakt, wenn man statt der Sonne den Schwerpunkt des Systems Sonne-Planet in den Brennpunkt der Bahnellipse setzt. Sie sind in der Kepler Gleichung ausgedrückt. Das dritte vernachlässigt die Planetenmasse gegenüber der Sonnenmasse; seine exakte Form lautet:
Eine unangenehme Begleiterscheinung der elliptischen Planetenbahnen ist, dass die Umlaufgeschwindigkeit der Erde um die Sonne (wegen des 2. Keplerschen Gesetzes) nicht konstant ist. Wenn die Erde im Winter näher an der Sonne steht ist ihre Geschwindigkeit größer als im Sommer, wenn sie weiter von der Sonne entfernt ist. Deshalb ist der Sonnentag (die Zeit zwischen zwei Mittagshöchstständen der Sonne über einem Punkt der Erde) im Winter etwas länger als im Sommer (da die Erde eine größere Strecke auf ihrer Bahn zurücklegt muss sie sich ein Stückchen weiter drehen, bis die Somme wieder den Höchststand erreicht hat). So sind die Sonnentage im Winter etas länger.
Kepler bewies die elliptische Form der Bahnen von Himmelskörpern um ein Zentralgestirn empirisch: seine Planetenortberechnungen waren einfach exakt. Isaak Newton konnte das dann mit der Erfindung eine neuen Kraft, die zwischen Zentralgestirn und Planet wirkt: der Gravitation erklären. Es blieb das Problem der Nichtlösbarkeit der Mondbahnberechnung (das drei Körperproblem). Ein analytischer Beweis für die elliptischen Planetenbahnen gelang erst Albert Einstein in seiner allgemeinen Relativitätstheorie.
Die Kepler-Gleichung.
Johannes Keplers konnte zeigen, dass man mit elliptischen Bahnen die Orte der Planeten zu einem beliebigen Zeitpunkt sehr viel ganauer vorhergesagt werden können. Allerdings stieß er auf das Problem, die Länge eines Ellipsenabschnitts zwischen zwei beliebigen Punkten in der Brennpunktsform der Ellipse berechnen zu müssen. Er musste die Länge des Ellipsenbogens vom sonnenfernsten Punkt, dem Aphel, kennen. Für diese Bestimmung benutzte Kepler die klassische Geometrie und erhielt die Kepler-Gleichung: M = E ± ε·sin E. Die Ausführungen dazu hat er im 5. Buch der Epitomes Astronomiae Corpernicanae etwas umständlich dargelegt. Ich habe die Gleichung hier moderner abgeleitet, aber mit den selben Grundlagen.
Kepler musste zur Berechnung der Planetenorte zu einer beliebigen Zeit des Umlaufes auf der elliptischen Bahn sowohl den Winkel M = ∢PBS, den die Verbindungslinie des Planeten zur Sonne in B vom Aphel S (sonnenfernster Punkt der Umlaufbahn) zum gegenwärtigen Punkt P einschließt, als auch die Entfernung r (Strecke BP) des Planeten zur Sonne bestimmen. Er nannte den Winkel M mittlere Anomalie.
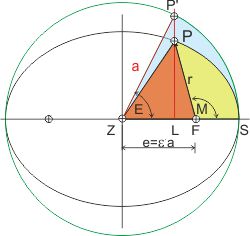 (Wegen der Übersichtlichkeit wähle ich eine Anordnung mit der Sonne im Brennpunkt F und der mittelren Anomalie ab dem Perihel gezählt (es ergibt sich das gleiche Ergebnis mit dem anderen Brennpunkt).
bediente sich der Affinität der Ellipse zum Kreis. Im Kreis kann man die Flächen der Segmente leicht berechnen. Und es gibt die Beziehungen von Elementen der Ellipse zu denen des Kreises aus den Sätzen des Apollonius von Perga.
(Wegen der Übersichtlichkeit wähle ich eine Anordnung mit der Sonne im Brennpunkt F und der mittelren Anomalie ab dem Perihel gezählt (es ergibt sich das gleiche Ergebnis mit dem anderen Brennpunkt).
bediente sich der Affinität der Ellipse zum Kreis. Im Kreis kann man die Flächen der Segmente leicht berechnen. Und es gibt die Beziehungen von Elementen der Ellipse zu denen des Kreises aus den Sätzen des Apollonius von Perga.
Er zeichnete also einen Umkreis der Ellipse mit dem Radius der großen Halbachse a (hier grün), um die Fläche des gelb gefärbten Ellipsensegments zu berechnen.
Apollonius von Perga (262 bis 190 v. Chr.) hatte die Erkenntnisse seiner Zeit über die Kegelschnitte in sieben Büchern zusammengefasst, von denen nur lateinische Übersetzungen "De Conicis" erhalten sind. Deren Kenntnis gehörte zum Bildungscanon eines Wissenschaftlers.
Keplers verwendet u. a. folgende Sätzen des Apollonius von Perga.
Umschreibt man eine Ellipse mit der großen Achse 2 · a und der kleinen 2 · b, mit dem Umkreis des Radius a, der die Ellipse in den beiden Scheiteln S und S' berührt, und zieht die Verbindungslinie (Apsidenlinie) zwischen den Scheiteln der Ellipse, sodass der gemeinsame Mittelpunkt Z und die Brennpunkte B und F der Ellipse auf der Apsidenlinie liegen, so gilt:
- Jede Sehne in einem Punkt L auf der Apsidenlinie, die auf der Apsidenlinie senkrecht steht, schneidet die Ellipse und den Kreis in der Weise, dass sich die Sehnenabschnitte der Ellipse zu denen des Kreises verhalten wie b zu a.
- Die Flächen von Ellipse und Umkreis verhalten sich wie b zu a.
- Zieht man Verbindungslinien von Punkten, die auf einem Lot und auf den Umfängen von Kreis und Ellipse liegen, zum Brennpunkt F, so verhalten sich die Flächen der Segmente wie die Abschnitte auf dem Lot.
- Teilt man den Kreisumfang durch solche Lote in beliebig viele gleiche Abschnitte, so wird die Ellipse durch die Schnittpunkte des Lots mit dem Ellipsenumfang in ungleiche Teile geteilt. Der Unterschied der Länge der Kreisabschnitte zu denen der Ellipsenabschnitte ist am Scheitel am größten, an der kleinen Achse am kleinsten.
- Der Ellipsenumfang ist sehr nahe am arithmetischen Mittel aus Umkreis- und Inkreisumfang.
Man erkennt, dass die exzentrische Anomalie E und die mittlere Anomalie M über das Dreieck ZFP verknüpft sind. Das wird durch das Lot LP' vermittelt, das Verhältis dessen Abschnitte LP' /frasl;&nsbp;LP = a /frasl;&nsbp;b ist aus dem 1. Lehrsatz des Apollonius von Perga bekannt. Keplers geht in seiner Argumentation wie folgt vor:
- Die Fläche des Kreissegments SZP′ entpricht dem Anteil des Winkels bei Z am Vollkreis:
<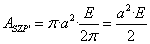
-
Die Fläche des Ellipsensegments SZP entpricht ebenso dem Anteil des Winkels bei Z am Vollkreis, weil die beiden Punkte P und P′ auf dem Lot liegen:
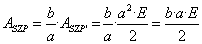
-
Die Höhe LP im Dreieck ZFP ergibt sie aus der Definition der Sinusfunktion:
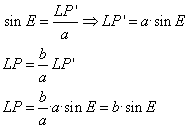
-
Damit ist die Fläche des Dreiecks ZFP:
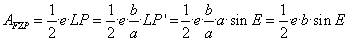
-
Die Fläche des Ellipsenabschnitts FSP ergibt sich als Differens der des Sektors ZSP und des Dreiecks ZFP:
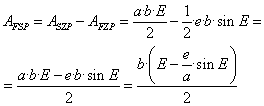
-
Wie unter 1. kann man die Fläche FSP auch als den Bruchteil der Gesamtfläche der Ellipse als Funktion von M ausdrücken:
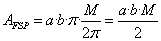
-
Die beiden so berechneten Flächen FSP müssen gleich sein:
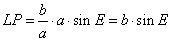
Diese Kepler-Gleichung setzt die exzentrische Anomalie E, das ist der Winkel zwischen der großen Achse und der Verbindungslinie am Mittelpunkt zu einem Punkt auf der Ellipse mit der mittleren Anomalie M, das ist der Winkel am Brennpunkt zwischen der großen Achse und der Verbindungslinie zu dem Punkt auf der Ellipse in Beziehung. Neben den Variablen E und M kommen nur die für jede Ellipse spezifische Konstante, die numerische Exzentrizität ε vor. Allerdings taucht die exzentrische Anomalie E als Argument einer transzendenten Winkelfunktion auf, die zyklisch ist und keine eindeutigen Ergebnisse liefert. Damit wird die Kepler-Gleichung eine transzendete Gleichung, d. h. man kann sie nicht lösen. Zur Zuordnung der Werte von E und M muß man die Werte der mittleren Anomalie M für einen Bereich der exzentrischen Anomalie E ausrechnen und die Wertepaare suchen, die gleich sind.
Nach 5. der obigen Regeln über die Ellipse und ihren Umkreis kann man den Umfang des Umkreises in regelmäßige Bogenstücke teilen, z. B. in 360 Teile. Jeder Teil einspricht dann einem 360tel der Umlaufzeit, oder einer Änderung des Winkels E um 1°. Der Winkel der exzentrischen Anomalie E kann also als Maß für die Zeit genommen werden, die ein Planet auf seiner Umlaufbahn vom Aphel zum gegenwärtigen Ort gebraucht hat.
Die mittlere Anomalie M dagegen ist über den Lotabschnitt mit der wahren Anomalie φ verknüpft. Wenn man also die zu einer exzentrischen Anomalie E gehörende mittlere Anomalie M kennt, kann man den Winkel φ zu beliebigen Zeiten des Umlaufs berechnen.
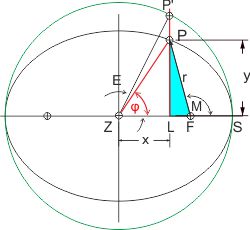 Der Fahrstrahl FP ist die Hypothenuse im blauen Dreieck LFP. Seine L࣮nge kann man mit dem Satz des Pythagoras berechnen:
Der Fahrstrahl FP ist die Hypothenuse im blauen Dreieck LFP. Seine L࣮nge kann man mit dem Satz des Pythagoras berechnen:
- r2 = LF2 + LP2
Die Kathete LP berechnet man mit der Definition der Sinusfunktion:
- sin E = LP′ ⁄ a
Nach Apollonius ist LP = b ⁄ a · LP′, eingesetzt:
Die andere Kathete LF ergibt sich als Differenz der linearen Exzentrizität e und dem Abstand LZ des Lotfußes L vom Mittelpunkt Z.
Einsetzen in die obige Formel für r2:
Ausmultiplizieren der Klammerausdrücke und substituieren von b2 = a2 - e2
Substituieren von sin2 E = 1 - cos2 E und sortieren:
Damit lautet der Ausdruck für die Länge des Fahrstrahls r in Abhängigkeit von der exzentrischen Anomalie E für eine Ellipse der linearen Exzentriziät e:
r = a - e · cos E
(Das Vorzeichen wechselt, wenn der gegenüberliegende Scheitel betrachtet wird, denn: cos α = −cos (α + 180°.)
Die wahre Anomalie φ ist der Winkel, den die Verbindungslinie des Mittelpunktes mit dem Planetenort auf der Ellipse. Sie spielt keine Rolle in der Theorie Keplers und hat nur eine historische Bedeutung in der Kopernikanischen Berechnung. Im Kopernikanischen System bewegen sich die Planeten auf konzentrischen Kreisbahnen um die Sonne, was zu Abweichungen der berechneten Planetenorten zum beobachteten führte. Die Abweichungen nannte man "Anomalie", und versuchte sie mit Epizyklen zu korrigieren. Kepler verwendet in seinem Werk Epitomes Astronomiae Copernicanae diese allen Astronomen geläufigen Begriffe. Das führte zu beträchtlichen Verwirrungen.
Wie sieht nun das Ergebnis aus? Nehmen wir einen hypothetischen Planeten, der auf einer elliptischen Bahn mit den Halbachsen a = 100 und b = 75 Längeneinheiten seine Sonne in 200 Zeiteinheiten umkreist (es ist unerheblich, in welchen Einheiten wir Zeit und Länge messen), und plotten wir seine Position in Intervallen von 5 Zeiteinheiten.

Rein qualitativ gibt das Bild aber schon das richtige Verhalten wieder. Im Perihel sind die Abstände der Punkte gering, dafür liegen lange Ellipsenbögen zwischen den Punkten. Auf der gegenüberliegenden Seite - im Aphel - sind Radien groß und die Winkeländerungen klein. Die Berechnung wird separat erläutert.
![]()
Der Beitrag Carl Friedrich Gauss′.
Carl Friedrich Gauss unternahm es, eine gemeinsame Differenzialgleichung für die Kegelschnitte aufzustellen. Ziel war es, mit wenigen Messungen innerhalb eines kurzen Zeitraumes die Bahnparameter von Himmelskörpern zu berechnen. Er beginnt das Werk mit der Betrachtung der Ellipse. Am Ende des Abschnitts 6. führt der Übersetzer aus:
Auf diese Weise ausgedrückt heisst die Grösse
die mittlere Anomalie, die daher im Verhältnis der Zeit wächst und zwar täglich um das Augment
-
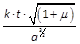 ,
,
welches man die mittlere tägliche Bewegung (motus medius diurnus) nennt. — Die mittlere Anomalie bezeichnen wir durch M.
Im Original "Theoria Motus Corporum Coelestium" heißt es auf Latein:
Hoc modo expressa quantitas
anomalia media vocatur, quae igitur in ratione temporis crescit, et quidem quotidie augmento
-
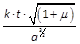 ,
,
quod motus medius diurnus dicitur. Anomaliam mediam per M denotabimus.
Da Herr Gauss in dem Buch keine erklärenden Abbildungen verwendet, wurde die Übersetzung so verstanden, dass die obige Formel die mittlere Anomalie ist (obwohl sie einige Zeilen vorher als excentrische Anomalie E bezeichnet wird). Das ist fatal, den die Formel gilt mit dem Mittelpunkt. So wird denn seither weitgehend eine falsche Herleitung der Keplergleichung gelehrt, und auch in seriösen Quellen angegeben.
- Quellen:
-
- Carl Friedrich Gauß: Theorie der Bewegung der Himmelskörper, welche in Kegelschnitten die Sonne umlaufen. Übersetzt von Carl Haase. Hannover 1865.
- Carolo Friedricco Gauss: Theoria Motus Corporum Coelestinum. Hamburg 1809.
© Rainer Stumpe, URL: www.rainerstumpe.de/
Datenschutzerklärung