Die Kegelschnitte
Im 5. und 4. Jahrhundert vor Christus griechische Mathematiker mit der Konstruktion von geometrischen Figuren. Ihre Werke sind wohl nur unvollständig im Original erhalten. Eine wichtiger Quelle ist Pappos Alexandrinus′ "Mathematicae Collectiones", die auch Johannes Kepler bekannt war und auf die er sich beim Beweis der elliptischen Planetenbahnen stützte.
Zu den Kegelschnitten arbeiteten Euklid (vier Bücher), Apollonius (8 Bücher auf der Basis Euklids) und Aristaios (zu spitzwinkligen, rechwinkligen und stumpfwinkligen Kegeln). Bei Euklid waren es rechtwinklige Kegel, die entstehen, wenn man ein rechtwinkliges Dreieck um eine der Kathethen dreht.
Die Kegelspitze kann man abschneiden und erhält dann einen Kegelstumpf. Apollonius untersuchte die Schnittlinien mit dem Kegelmantel für unterschiedliche Schnittwinkel und fand die Ellipse, die Parabel und die Hyperbel — je nach der Neigung der schneidenden Ebene.
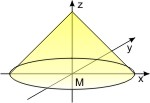 Der gerade Kreiskegel hat als Grundfläche einen Kreis, und die Verbindungslinie der Kegelspitze mit dem Mittelpunkt der Grundfläche (Kegelhöhe) steht senkrecht auf der Basis. Seine Mantelfläche wird beschrieben durch die Formel: a · x2 + b · y2 = c ·z2. Beim Einheitskegel ist a = b = c = 1.
Der gerade Kreiskegel hat als Grundfläche einen Kreis, und die Verbindungslinie der Kegelspitze mit dem Mittelpunkt der Grundfläche (Kegelhöhe) steht senkrecht auf der Basis. Seine Mantelfläche wird beschrieben durch die Formel: a · x2 + b · y2 = c ·z2. Beim Einheitskegel ist a = b = c = 1.
In der analytischen Geometrie wird eine Ebene durch die Formel a · x + b ·y + c · z = d. (a, b, c, d sind Konstanten.) Alle Punkte für die sowohl die Kegelgleichung wie die Ebenengleichung erfüllt sind, ergeben den Schnitt der beiden.
Die Ellipse
 Die Form der Kegelschnitte hängt außerdem vom Winkel β ab, den die Mantellinie des Kegels mit der Horizontalen einschließt. Als Maß führt man die numerische Exzentrizität ε ein. Sie ist das Verhältnis des Sinuswerte der Winkel α und β: ε = sin α ⁄ sin β. Im Falle der Ellipse ist der Winkel α kleiner ist als der Winkel β. Dann ist auch sin α kleiner als sin β, und der Quotient ε ist kleiner als 1.
Die Form der Kegelschnitte hängt außerdem vom Winkel β ab, den die Mantellinie des Kegels mit der Horizontalen einschließt. Als Maß führt man die numerische Exzentrizität ε ein. Sie ist das Verhältnis des Sinuswerte der Winkel α und β: ε = sin α ⁄ sin β. Im Falle der Ellipse ist der Winkel α kleiner ist als der Winkel β. Dann ist auch sin α kleiner als sin β, und der Quotient ε ist kleiner als 1.
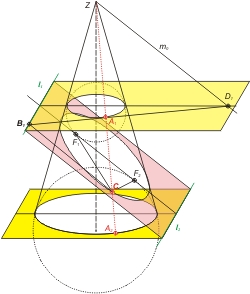
In der Abbildung sind auch die beiden Dandelinschen Kugeln eingezeichnet. Sie werden dem Kegel so eingeschrieben, dass sie die Ellipse in den Brennpunkten berühren (rote Punkte). Die Ebenen, in denen die Kugeln den Kegelmantel berühren (hier gelb), parallel zur Grundfläche des Kegels, schneiden sich mit der Ebene, die die Ellipse aus der Kegelhülle ausschneidet (hier rot), in den Leitlinien (grün, strichpunktiert). Die Eigenschaften der Ellipse sind an anderer Stelle ausführlich erklärt; dort werden auch abgeleitet:
- die Mittelpunktsgleichung,
- die Brennpunktsgleichung und
- die Scheitelgleichung.
Die Parabel
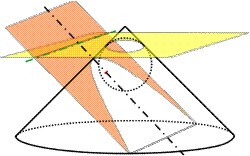 Um eine Parabel zu erzeugen, muß die den Kegel schneidende Ebene parallel zur Hülle des Kegels liegen. Es ist also α = β oder ε = 1. Die beiden Äste der Parabel schneiden sich nie und verlaufen erst im Unendlichen parallel zu einander.
Um eine Parabel zu erzeugen, muß die den Kegel schneidende Ebene parallel zur Hülle des Kegels liegen. Es ist also α = β oder ε = 1. Die beiden Äste der Parabel schneiden sich nie und verlaufen erst im Unendlichen parallel zu einander.
Bei der Parabel gibt es nur einen Berührungspunkt der Dandelinschen Kugel, der als Brennpunkt der Parabel bezeichnet wird, und eine Leitlinie, die sich wie bei Ellipse und Hyperbel ergibt. Die Leitlinie hat vom einzigen Brennpunkt den Abstand p, den Parameter der Parabel (die Sehne senkrecht zur Achse der Parabel durch den Brennpunkt hat die Länge 2 · p).
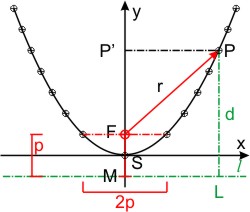 Die Parabel hat nur einen Brennpunkt, der andere liegt im "unendlichen". Sie ist symmetrisch zur ihrer (y-) Achse, und zu jedem Punkt P(x,y) auf einem der Zweige gibt es daher einen zweiten P(-x,y), dessen Koordinaten sich nur im Vorzeichen der x-Koordinate unterscheiden.
Die Parabel hat nur einen Brennpunkt, der andere liegt im "unendlichen". Sie ist symmetrisch zur ihrer (y-) Achse, und zu jedem Punkt P(x,y) auf einem der Zweige gibt es daher einen zweiten P(-x,y), dessen Koordinaten sich nur im Vorzeichen der x-Koordinate unterscheiden.
Jeder Punkt P auf der Parabel hat vom Brennpunkt F den gleichen Abstand r wie von der Leitlinie l: r = d. Im Koordinatensystem mit dem Scheitel S der Parabel im Ursprung hat der Brennpunkt F den Abstand FS = p ⁄ 2. Die Länge des Fahrstrahls zum Punkt P(x,y) errechnet man nach Pythagoras im Dreieck FPP′:
- r² = (y - p ⁄ 2)² + x²,
- also
- r = √[(y - p ⁄ 2)² + x²].
Der Abstand d des Punktes P von der Leitlinie l ist: d = y+ p ⁄ 2.
Wegen der Bedingung für die Parabel (r = d) ist damit r² = (y - p ⁄ 2)² + x² = d² = (y + p ⁄ 2)². Ausmultiplizieren ergibt:
- y² - 2 · p ⁄ 2 · y + (p ⁄ 2)² + x² = y² + 2 · p ⁄ 2 · y + (p ⁄ 2)²
- und kürzen und auflösen nach x² führt schließlich zur Scheitelgleichung der Parabel:
- x² = 2·p · y.
Natürlich gibt es auch noch andere Formeln für die Parabel — analog zur Ellipse — die findet man aber auch an anderer Stelle im Web abgeleitet.
Die Hyperbel
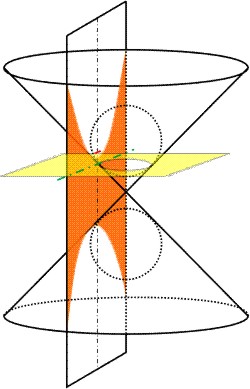 Schneidet die erzeugende Ebene parallel zur Kegelachse den Doppelkegel, so entsteht eine Hyperbel. Eine hyperbelerzeugende Schnittebene muß schneidet beide Teile des Doppelkegels. Deshalb hat sie zwei Äste, und ist symmetrisch zur Verbindunglinie der beiden Scheitel S1,2 und auch zur Senkrechten im Mittelpunkt M (wie übrigens auch die Ellipse).
Schneidet die erzeugende Ebene parallel zur Kegelachse den Doppelkegel, so entsteht eine Hyperbel. Eine hyperbelerzeugende Schnittebene muß schneidet beide Teile des Doppelkegels. Deshalb hat sie zwei Äste, und ist symmetrisch zur Verbindunglinie der beiden Scheitel S1,2 und auch zur Senkrechten im Mittelpunkt M (wie übrigens auch die Ellipse).
Auch hier gibt es zwei Dandelinschen Kugeln, die die schneidende Ebene in den Brennpunkten der Hyperbel berühren, und die Schnittlinie der Ebenen durch die Berührungskreise der Dandelinschen Kugeln mit der erzeugenden Ebene sind die Leitlinien der Hyperbel.
Die Hyperbel wird beschrieben durch die Linien auf dem Kegelmantel, die die Schnittebene mit dem Mantel gemeinsam habeb. Es sind dies die Asymptoten, denen sich die Äste der Hyperbel "asymptotisch" annähern. Die Asymptoten schneiden sich im Mittelpunkt M der Hyperbel. Sie schließen den Winkel 2 · α ein, den Öffnungswinkel an der Kegelspitze.
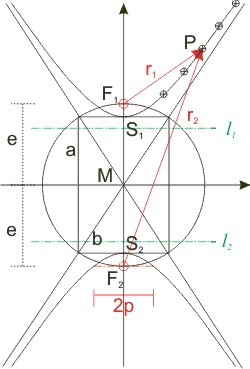 Die beiden Scheitel haben den Abstand a (bei der Ellipse die große Halbachse, die kleine gibt es bei der Hyperbel nicht, sie ist aber die kürzere Seite im Rechteck aus den Schnittpunkten eines Kreises mit dem Radius der linearen Exzentrizität e mit den Asymptoten). Dieser Kreis schneidet die Achse durch die Scheitel in den beiden Brennpunkten F1 und F2 (deren Abstand vom Mittelpunkt M ist die lineare Exzentrizität e — wie bei der Ellipse). Während bei der Ellipse die Summe der beiden Brennstrahlen konstant ist, ist es bei der Hyperbel die Differenz der Brennstrahlen r2 - r1 = 2 · a. Deshalb lautet die Mittelpunktsgleichung der Hyperbel:
Die beiden Scheitel haben den Abstand a (bei der Ellipse die große Halbachse, die kleine gibt es bei der Hyperbel nicht, sie ist aber die kürzere Seite im Rechteck aus den Schnittpunkten eines Kreises mit dem Radius der linearen Exzentrizität e mit den Asymptoten). Dieser Kreis schneidet die Achse durch die Scheitel in den beiden Brennpunkten F1 und F2 (deren Abstand vom Mittelpunkt M ist die lineare Exzentrizität e — wie bei der Ellipse). Während bei der Ellipse die Summe der beiden Brennstrahlen konstant ist, ist es bei der Hyperbel die Differenz der Brennstrahlen r2 - r1 = 2 · a. Deshalb lautet die Mittelpunktsgleichung der Hyperbel:
Bei der Hyperbel gibt es zwei Leitlinien l1 und l2. Ihre Abstände von von den Scheiteln S1,2 ist y1,2 = ± a² ⁄ e. Der Scheitel S1 hat vom Mittelpunkt den Abstand a. Im Koordinatensystem mit dem Scheitel im Ursprung ergibt sich aus der Mittelpunktsgleichung für die y-Koordinate des Punktes P also mit 2 · p als Länge der Sehne durch den Brennpunkt:
Vergleich der Scheitelgleichungen der Kegelschnitte
Die Scheitelgleichungen der Kegelschnitte werden in allen zeitgenössischen Quellen gegenübergestellt, weil mit ihnen die Bezeichnungen aus dem Griechischen ableiten lassen. Aber offensichtlich ist der Hintergrund der griechischen Namensgebung in Vergessenheit geraten. (Im Grunde könnte man natürlich auch die Mittelpunktsgleichungen von Ellipse und Hyperbel vergleichen, allerdings hat die Parabel keinen Mittelpunkt.) Also will ich es weiter unten herleiten.
| Parabel | : | y² = 2 · p · x |
| Ellipse | : | y² = 2 · p · x - p · x² ⁄ a |
| Hyperbel | : | y² = 2·p · x + p · x² ⁄ a |
| gemeinsame Scheitelgleichung | : | y² = 2 · p · x - (1 - ε²) · x² |
Die Bedeutung der Scheitelgleichung und das "Gnomon"
Die Scheitelgleichungen der Kegelschnitte werden in aktuelleren Quellen etwas düftig behandelt. (Für Problemlösungen seit Kepler seine Gleichung veröffentlichte, sind auch die Mittelpunkts- und vorallem die Brennpunktsgleichung interessanter.) Man muß schon ein wenig zurück gehen, um die Bedeutung der Scheitelgleichung zu finden — bis zu Euklid. In Keplers Liber Quintus gibt es eine hübsche Anwendung für das Gnomon.
Unter anderen interpretiert Prof. Dörte Haftendorn, Uni Lüneburg, die Namensgebung Parabel (παραβαλλειν: paraballein, gleichkommen), Hyperbel (μπερβαλλειν: hyperballein, übersteigen) und Ellipse (ελλειπειν: elleipein, ermangeln) mit dem gemeinsamen Glied 2 · p · x, das bei der Parabel fehlt, bei der Hyperbel um (p ⁄ a) · x² vergrößert und bei der Ellipse verringert wird.
Helmuth Gericke3 weist auf die Lösung quadratischer Gleichungen durch geometrische Konstruktion der griechischen Mathematiker mit dem "Gnomon" hin. Da Kepler diese Rechenmethode im Kapitel III (De figura orbita) des Liber Quintus anwendet soll sie kurz erläutert werden.
Gericke bezieht sich in seinem Buch3 auf Euklids Lehrsatz 5 im 2. Buch:
Teilt man eine Strecke sowohl in gleiche als auch in ungleiche Abschitte, so ist das Rechteck aus den ungleichen Abschnitten der ganzen Strecke zusammen mit dem Quadrat über der Strecke zwischen den Teilpunkten dem Quadrat über der Hälfte gleich.
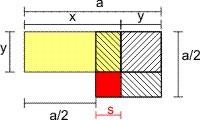 Das Bild stellt den Lehrsatz Euklids dar. Nun soll die Fläche des gelben Rechtecks plus die des roten kleinen Quadrats unten links gleich der Fläche des schraffierten Quadrats sein. Die Rechteckfläche ist x·y, die des großen Quadrats (a ⁄ 2)² = (x + y)². Das kleine Quadrat hat die Fläche
Das Bild stellt den Lehrsatz Euklids dar. Nun soll die Fläche des gelben Rechtecks plus die des roten kleinen Quadrats unten links gleich der Fläche des schraffierten Quadrats sein. Die Rechteckfläche ist x·y, die des großen Quadrats (a ⁄ 2)² = (x + y)². Das kleine Quadrat hat die Fläche
- ((a ⁄ 2) - y)² = ((x - y) ⁄ 2)².
- Also:
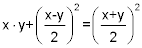
In geometrischen Größen ausgedrückt: die Fläche des nicht-schraffierten Teil des gelben Rechtecks ist gleich der daneben liegenden schraffierten Fläche, und die beiden schraffierten Rechtecke sind gleich groß. Also erhält man die Fläche des gelben Rechtecks als Differenz des großen Quadrats und des kleinen roten Quadrats. (Die schraffierte, L-förmige Fläche nennt Euklid ein Gnomon.)
Damit hat man zwei Strecken gefunden, deren Summe x + y = a ist, und deren Produkt die Fläche c² ist. Die Gleichung dazu ist x · (a - x) = c². Die kann man umformen: x² - a · x = c². Das entspricht der Form nach der Scheitelgleichung der Ellipse, wo a = 2 · p.
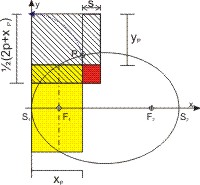 Mit dieser Gnomonkonstruktion kann man z. B. die y-Koordinate eines Ellipsenpunktes für eine beliebige x-Koordinate konstruieren. Man konstuiert das Gnomon der Fläche des Rechtecks aus dem Ellipsenparameter 2·p und der x-Koordinate des Punktes P, xP, und findet die y-Koordinate yP. Auf der y-Achse wird die Strecke 2 · p um xP verlängert, und die resultierende Strecke halbiert. Auf ihr errichtet man das Quadrat. Die Gnomonfläche (schraffiert plus das rote Quadrat) ist FG = [(2 · p + xP) ⁄ 2]² - yP². Sie ist gleich der gelben Rechteckfläche 2 · p·xP plus dem roten Quadrat.
Mit dieser Gnomonkonstruktion kann man z. B. die y-Koordinate eines Ellipsenpunktes für eine beliebige x-Koordinate konstruieren. Man konstuiert das Gnomon der Fläche des Rechtecks aus dem Ellipsenparameter 2·p und der x-Koordinate des Punktes P, xP, und findet die y-Koordinate yP. Auf der y-Achse wird die Strecke 2 · p um xP verlängert, und die resultierende Strecke halbiert. Auf ihr errichtet man das Quadrat. Die Gnomonfläche (schraffiert plus das rote Quadrat) ist FG = [(2 · p + xP) ⁄ 2]² - yP². Sie ist gleich der gelben Rechteckfläche 2 · p·xP plus dem roten Quadrat.
Das Gnomon bei Hyperbel und Parabel
Ähnliche Konstruktionen gibt es auch für die Koordinaten eines Punktes auf der Parabel bzw. auf der Hyperbel. Eine ausführliche Darstellung der Euclidis Elementa findet man von David E. Joyce4.
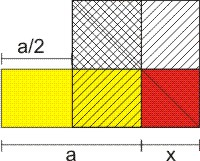 Das Gnomon eines Hyperbelpunktes (rechts oben nach links unten schraffiert) konstruiert man aus dem gelben Rechteck mit Kantenlänge a über ein Hilfsquadrat mit der Seitenlänge a ⁄ 2 (links oben nach rechts unten schraffiert) das rote Quadrat.
Das Gnomon eines Hyperbelpunktes (rechts oben nach links unten schraffiert) konstruiert man aus dem gelben Rechteck mit Kantenlänge a über ein Hilfsquadrat mit der Seitenlänge a ⁄ 2 (links oben nach rechts unten schraffiert) das rote Quadrat.
Die Anleitung findet man bei Euclids Elementa im Buch 2, Lehrsatz 5. Es löst die Gleichung x² - b·x = C, also die Scheitelgleichung der Hyperbel.
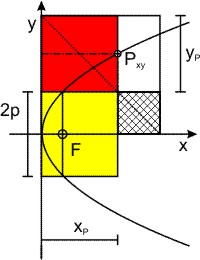 Um die y-Koordinate des Punktes Px,y auf einem Ast der Hyperbel zu erhalten, zeichnet man ein Rechteck (hier gelb) mit den Seiten 2·p und yP, das man ein Quadrat mit der Seitenlänge p anschließt (hier schraffiert). Die Diagonale des Quadrats verlängert man über die Ecke des Rechtecks bis zur y-Koordiante. Das rote Rechteck hat dann die Seiten xP und yP.
Um die y-Koordinate des Punktes Px,y auf einem Ast der Hyperbel zu erhalten, zeichnet man ein Rechteck (hier gelb) mit den Seiten 2·p und yP, das man ein Quadrat mit der Seitenlänge p anschließt (hier schraffiert). Die Diagonale des Quadrats verlängert man über die Ecke des Rechtecks bis zur y-Koordiante. Das rote Rechteck hat dann die Seiten xP und yP.
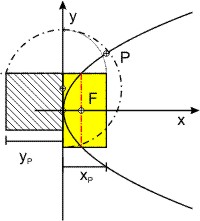 Einfacher ist die Konstruktion der y-Koordinate eines Parabelpunktes Px,y, da man das gelbe Rechteck nur in ein Quadrat umzuwandeln hat.
Einfacher ist die Konstruktion der y-Koordinate eines Parabelpunktes Px,y, da man das gelbe Rechteck nur in ein Quadrat umzuwandeln hat.
Man zeichnet wieder ein Rechteck mit den Seiten 2 · p und xP und verlängert die lange Seite um xP. Die Streckensumme aus 2 · p und xP wird halbiert und um den Halbierungspunkt wird ein Kreis mit dem Radius (2 · p + xP) ⁄ 2 geschlagen, der die Verlängerung der kürzeren Rechteckseite schneidet. Der Abstand des Schnittpunktes von der y-Koordinate ist die gesuchte Koordinate yP des Parabelpunktes.
Die Leitlinie und die Dandelinsche Kugel
Eine Ellipse ist die Schnittlinie einer Ebene (hier rot) mit einem geraden Kreiskegel. Dem Kegel kann man zwei Dandelinsche Kugeln so einschreiben, dass sie die Schnittebene in den Punkten F1 und F2 berühren. Die Berührungspunkte sind die Brennpunkte der Ellipse. Diese Dandelinschen Kugeln erzeugen mit dem Kegelmantel jeweils einen Berührungskreis, der eine Ebene senkrecht zur Kegelachse definieren (hier gelb). Die beiden gelben Ebenen schneiden die rote Schnittebene in je einer Geraden (grün): den Leitlinien l1 und l2. Eine Ebene Σ, die die Achse des Kegels enthält und auf den beiden Leitlinie senkrecht steht, schneidet die Ellipse in deren großer Achse; die Brennpunkte liegen auf dieser Schnittlinie. Eine Parallele m0 zur großen Achse der Ellipse durch F1 und F2 in dieser Ebene schneidet die gelbe Ebene in D1 (der Schnittpunkt auf der unteren gelben Ebene D2 liegt außerhalb der Skizze).
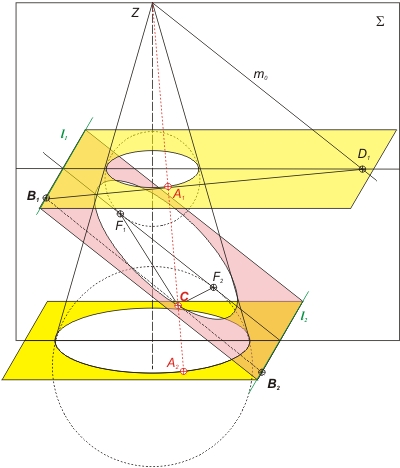
Dreht man diese Ebene Σ um m0 als Achse um einen gewissen Winkel ξ, so bleibt sie parallel zur großen Ellipsenachse, und schneidet die rote Ebene in der Linie B1B2. Es ensteht außerdem eine eine Schnittlinie ZA1A2 (rot) mit dem Mantel des Kegels. Der Schnittpunkt C der Linie B1B2 in der roten Ebene mit der Mantellinie A1A2 liegt auf der Ellipse. Die beiden Punkte A1 und F1 sind die Berührungspunkte von Tangenten aus C an die obere Kugel. Die Tangentenabschnitte CF1 und CA1 sind gleichlang. Das Gleiche gilt für die Tangenten an die untere Kugel: CF2 = CA2. Nach der Definition der Ellipse ist CF1 + CF2 = 2·a (a ist die große Halbachse). Damit wird CF1 + CF2 = A1A2 = 2·a.
In der um die Achse m0 gedrehten Ebene liegen die Punkte A1, B1, D1 und Z und somit auch die sich schneidenden Verbindungslinien ZA1 und B1D1. Diese Linien werden durch die zu einander parallelen Verbindungslinien ZD1 = m0 und B1B2 geschnitten. Damit gilt nach dem Strahlensatz für die Verhältnisse der Strecken auf den Schenkeln: CA1 : CB1 = ZA1 : ZD1 = CF1 : CB1 = ε. Und der Abstand der Leitlinie vom Mittelpunkt beträgt a2 ⁄ e.
Die Hyperbel hat ebenfalls zwei, die Parabel nur eine Dandelinsche Kugel.
- Germinal Pierre Dandelin
- Belgischer Mathematiker, geb. 12.04.1794 in LeBourget, gest. 15.02.1847 in Brüssel. Bewies dass die nach ihm benannten Kugeln einen Kegelschnitt in den Brennpunkten berühren. Offizier der Pioniere. Beschäftigte sich mit Geometrie. (Quelle: School of Mathematics and Statistics, University of St Andrews, Scotland)
- Adolf Wildbrett: Analytische Geometrie, Bayerischer Schulbuch-Verlag, 1948.
- Mathematik-Ratgeber (Herausg. W. Gellert), VEB Bibliographisches Institut Leipzig, 1984.
- Helmuth Gericke, Mathematik in Antike und Orient, Springer-Verlag Heidelberg Berlin, 1984.
- David E. Joyce, Euclid's Elements, Math and Computer Science, Clark University, Worcester, MA, USA.
- Joh. Jos. Ign. Hoffmann: Die geometrischen Bücher der Elemente des Euclides; als Leitfaden zum Unterrichte in der Elementar-Geometrie, Mainz, 1829.
© Rainer Stumpe, URL: www.rainerstumpe.de/
Datenschutzerklärung
