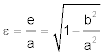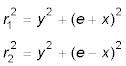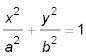Die Geometrie der Ellipse.
- Die lineare Exzentrizität.
- Die numerische Exzentrizität.
- Die Mittelpunktgleichung.
- Die Brennpunktgleichung.
- Die Scheitelpunktgleichung.
- Der Umfang der Ellipse.
- Die Fläche des Ellipsensektors.
- Die Kepler-Gleichung.
Unter den drei Kegelschnitten hat die Ellipse historisch eine herausragende praktische Bedeutung durch die Theorie zur Planetenbewegung von Johannes Kepler erhalten. Aus seinem Buch Epitomes Astronomiæ Copernicanæ habe ich die Darstellung des Liber Quintus erfasst. Hier entwickelt Keplerseine Argumentation, die schließlich in der Kepler-Gleichung mündet. Um die Entwicklung der Gedanken zu verstehen, muss man sich mit den geometrischen Eigenschaften vertraut machen.
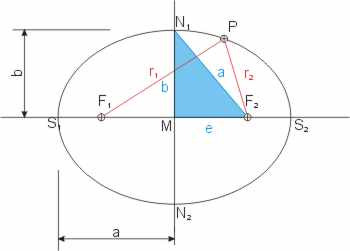 Betrachten wir die Ellipse. Jeder Punkt P auf ihr hat von zwei Punkten F1 und F2 den gleichen Abstand r1 + r2 = 2 · a. (Auf dieser Definition basiert die Gärtnerkonstruktion der Ellipse.) Die Ellipse sieht aus, wie ein gestauchter Kreis. Statt eines Radius gibt es zwei, die große (a) und kleine (b) Halbachse heißen. Die beiden Punkte F1 und F2 sind die Brennpunkte der Ellipse. Sie liegen auf der Hauptachse und die schneidet die Ellipse in den Hauptscheiteln S1 und S2. Die Nebenachse steht auf der Hauptachse senkrecht und geht durch den Mittelpunkt M der Ellipse. Ihre Schnittpunkte mit der Ellipse sind die Nebenscheitel N1 und N2. Es gilt im rechtwinkligen blauen Dreieck der Satz des Pythagoras: a2 = b2 + e2, wobei e die lineare Exzentrizität genannt wird.
Betrachten wir die Ellipse. Jeder Punkt P auf ihr hat von zwei Punkten F1 und F2 den gleichen Abstand r1 + r2 = 2 · a. (Auf dieser Definition basiert die Gärtnerkonstruktion der Ellipse.) Die Ellipse sieht aus, wie ein gestauchter Kreis. Statt eines Radius gibt es zwei, die große (a) und kleine (b) Halbachse heißen. Die beiden Punkte F1 und F2 sind die Brennpunkte der Ellipse. Sie liegen auf der Hauptachse und die schneidet die Ellipse in den Hauptscheiteln S1 und S2. Die Nebenachse steht auf der Hauptachse senkrecht und geht durch den Mittelpunkt M der Ellipse. Ihre Schnittpunkte mit der Ellipse sind die Nebenscheitel N1 und N2. Es gilt im rechtwinkligen blauen Dreieck der Satz des Pythagoras: a2 = b2 + e2, wobei e die lineare Exzentrizität genannt wird.
Hinweis:Bei einer gegebenen Ellipse findet man die Brennpunkte als Schnittpunkte eines Kreises mit dem Radius der großen Halbachse um einen Nebenscheitel mit der großen Achse.
Die charakteristischen Parameter der Ellipse
Die lineare Exzentrizität
Die Abstände der Brennpunkte F1, 2 vom Mittelpunkt sind gleich. Man nennt den Abstand MF1 = MF2 die lineare Exzentrizität e oder die Brennweite der Ellipse. Man berechnet e nach Pythagoras im rechtwinkligen, blauen Dreieck. Da der Nebenscheitel N1 ein Punkt auf der Ellipse ist, beträgt sein Abstand von den Brennpunkten 2 · a. Die Hypotenuse im blauen Dreieck hat also die Läge a, die senkrechte Kathete entspricht der kleinen Halbachse. Also gilt b2 + e2 = a2, oder:
![]()
Die numerische Exzentrizität
Zur Navigation interessiert uns besonders der Abstand zweier Punkte auf der Ellipse. Aber schon die Berechnung des Umfangs ist mit einfachen Mitteln nicht mehr zu bewerkstelligen. Das geht nur durch Integrieren einer Differentialgleichung in Polarkoordinaten. Um die Formeln abzuleiten, brauchen wir noch die numerische Exzentrizität ε.
 Die numerische Exzentrizität ε ist definiert als Quotient aus linearer Exzentrizität e und der Länge a der großen Halbachse:
Die numerische Exzentrizität ε ist definiert als Quotient aus linearer Exzentrizität e und der Länge a der großen Halbachse:
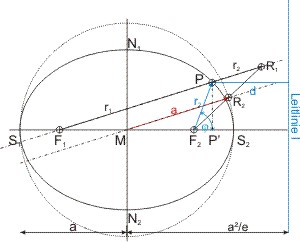
Die Leitlinie l ist geometrisch am Kegel erkennbar. Sie liegt parallel zur Nebenachse und schneidet die Apsidenlinie (x-Achse) so, dass ihr Abstand vom Scheitel S2 sich zu dem des Brennpunkts F2 verhält wie die große Halbachse a zur linearen Exzentrizität. Ihr Abstand vom Mittelpunkt M der Ellipse ist a2 ⁄ e. Das Verhältnis der Abstände jedes Punktes P auf der Ellipse vom Brennpunkt F2 und dieser Leitlinie ist konstant r2 ⁄ d = konstant.
Die Leitlinie l hat vom Scheitel S2 den Abstand (a2 ⁄ e) - a, und ein Ellipsenpunkt P den Abstand d = a2 ⁄ e - x (x ist die x-Koordinate des Punktes P und entspricht der Strecke MP′). Die Abstände r1 und r2 des Ellipsenpunktes P von den beiden Brennpunkten F1 und F2 sind die Hypotenusen in den rechtwinkligen Dreiecken F1PP′ bzw. F2PP′. Die beiden Dreiecke haben die Kathete y = PP′ gemeinsam, die anderen Katheten haben die Längen F1P′ = 2·e + (x - e) und F2P′ = x - e.
Mit dem Satz des Pythagoras können wir nun zwei Gleichungen für die Kathete y aufstellen:
- im Dreieck F1PP′: y² = r1² - (2·e + (x - e))²
- im Dreieck F2PP′: y² = r2² - (x - e)²
- damit:
- r1² - (x + e)² = r2² - (x - e)²
Aufgelöst nach r1² und ausmultipliziert ergibt: r1² = r2² + 4·e·x, oder r1² - r2² = 4·e·x = (r1 + r2)·(r1 - r2).
Da r1 + r2 = 2·a kann man die vorige Gleichung dividieren und erhält r1 - r2 = 2·e·x ⁄ a. Oder nach Einsetzen der Definition der Ellipse und aufgelöst: r1 = a + e·x ⁄ a bzw. r2 = a - e·x ⁄ a.
Diese letzte Gleichung kann man auf beiden Seiten mit a multiplizieren und nach x auflösen: x = (a² - r1·a) ⁄e. Diesen Ausdruck für x setzt man in die Gleichung für den Abstand d des Ellipsenpunkts P von der Leitlinie ein, und erhält: d = r1·(a ⁄ e). Daraus die Beziehung d ⁄ r1 = a ⁄ e. Damit ist gezeigt, dass das Verhältnis der Abstände eines beliebigen Ellipsenpunktes vom Brennpunkt und von der Leitlinie konstant ist, und nur von Parametern der Ellipse abhängt. Der Kehrwert dieses Verhältnisses wird numerische Exzentrizität ε genannt. Anschaulich erkennt man die numerische Exzentrizität aus dem Bild der Entstehung der Kegelschnitte.
In der Abbildung oben iat auch eine geometrische Konstruktion der numerische Exzentrizität eingezeichnet. Man verlängert den Strahl vom entfernteren Brennpunkt F1 zum Punkt P auf der Ellipse um den Abstand von P zum näheren Brennpunkt r2, und erhält den Punkt R1. Der Schnittpunkt einer Parallelen zu PR1 (= 2·a) durch den Mittelpunkt der Ellipse schneidet die Verbindungslinie von R1 und F2 im Punkt R2, der auch auf dem Umkreis der Ellipse liegt. MF2 = e und MR2 = a. Mit Hilfe eines Proportionallineals kann man nun das Verhältnis e ⁄ a berechnen. (Edmund Gunter erklärt das ausführlich im 2. Buch des Sectors, Kap. II unter 5.)
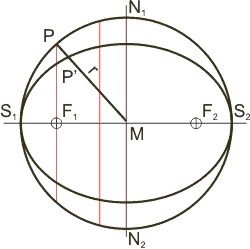 Die Ellipse ist ein affines Abbild des Kreises — man staucht den Kreis einlang einer der Achsen und erhält die Ellipse. Daher spielt der Kreis, aus dem die Ellipse entstanden ist, für viele Berechnungen der Ellipse nach der Euclidschen Trigonometrie eine ausschlaggebende Rolle. Beispiele sind Kepler, Newton und Gauss. Der Durchmesser des Umkreises ist gleich der großen Ellipsenachse, die Mittelpunkte von Ellipse und Umkreis fallen zusammen. Nach Appolonius von Perge verhalten sich die Sehnen von Ellipse und Kreis, die senkrecht auf der großen Achse stehen, wie die kleine zur großen Halbachse der Ellipse. Die Sehne, die durch einen der Brennpunkte der Ellipse geht, heißt Ellipsenparameter 2·p. Man berechnet sie im rechtwinkligen Dreieck ΔP'F1M aus der großen und der kleinen Halbachse, a bzw. b, nach dem Satz von Pythagoras. Bekannt sind ja die Hypotenuse r = a und die Strecke MF1 = e (die lineare Exzentrizität); daraus erhält man die Länge der Halbsehne F1P', und die verhält sich zur Ellipsenhalbsehne F1P wie die große Halbachse der Ellipse a zur kleinen b.
Die Ellipse ist ein affines Abbild des Kreises — man staucht den Kreis einlang einer der Achsen und erhält die Ellipse. Daher spielt der Kreis, aus dem die Ellipse entstanden ist, für viele Berechnungen der Ellipse nach der Euclidschen Trigonometrie eine ausschlaggebende Rolle. Beispiele sind Kepler, Newton und Gauss. Der Durchmesser des Umkreises ist gleich der großen Ellipsenachse, die Mittelpunkte von Ellipse und Umkreis fallen zusammen. Nach Appolonius von Perge verhalten sich die Sehnen von Ellipse und Kreis, die senkrecht auf der großen Achse stehen, wie die kleine zur großen Halbachse der Ellipse. Die Sehne, die durch einen der Brennpunkte der Ellipse geht, heißt Ellipsenparameter 2·p. Man berechnet sie im rechtwinkligen Dreieck ΔP'F1M aus der großen und der kleinen Halbachse, a bzw. b, nach dem Satz von Pythagoras. Bekannt sind ja die Hypotenuse r = a und die Strecke MF1 = e (die lineare Exzentrizität); daraus erhält man die Länge der Halbsehne F1P', und die verhält sich zur Ellipsenhalbsehne F1P wie die große Halbachse der Ellipse a zur kleinen b.
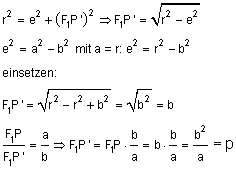
- Also: p = b² ⁄a.
Dieser Zusammenhang von Ellipse und Umkreis ermöglichte Kepler, seine Gesetze mathematisch abzuleiten (ebenso verwenden Newton und Gauss den "Ellipsenparameter").
Die sieben Bücher des Appolonius von Perge sind im Web zu finden.
Die Mittelpunktgleichung der Ellipse.
Kartesische Koordinaten
Die Ellipse wird definiert als die Kurve, auf der für alle Punkte P(x,y) die Summe der Abstände zu den beiden Brennpunkten F1,2 konstant ist PF1 + PF2 = r1 + r2 = konstant. Diese Konstante ist das zweifache der großen Halbachse a: r1 + r2 = 2 · a.
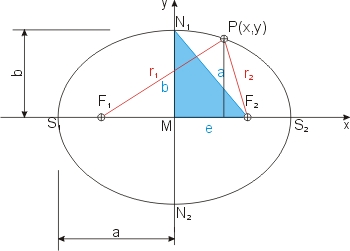 Mit dem Lot von P auf die x-Achse erzeugen wir zwei rechtwinklige Dreiecke, die r1 bzw. r2 als
Hypotenuse haben, und eine Kathete gemeinsam haben (deren Länge ist y). Wir können den Satz des Pythagoras anwenden und erhalten:
Mit dem Lot von P auf die x-Achse erzeugen wir zwei rechtwinklige Dreiecke, die r1 bzw. r2 als
Hypotenuse haben, und eine Kathete gemeinsam haben (deren Länge ist y). Wir können den Satz des Pythagoras anwenden und erhalten:
Mit der Definition der Ellipse (r1 + r2 = 2·a) erhalten wir durch Umformen und Einsetzen die Mittelpunktsgleichung der Ellipse:
Mit dieser Gleichung können wir nun die Koordinate x oder y eines Punktes P(x,y) aus der jeweils anderen berechnen, der auf der Ellipse mit den Halbachsen a und b liegt.
Carl Friedrich Gauss leitete hieraus eine lineare Ellipsengleichung ab, die er differenzieren konnte:
- r + αx + βy = γ
Dabei ist r der Fahrstrahl des Planeten, α · x = r1 und β · y = r2.
Polarkoordinaten
Polarkoordinaten beschreiben die Lage eines Punktes durch den Abstand ρ vom Koordinatennullpunkt und den Winkel φ, den dieser vom Mittelpunkt ausgehende Strahl mit der x-Achse einschließt. Auf der Ellipse muß man nun einen Ausdruck für den Abstand ρ und den Winkel φ finden.
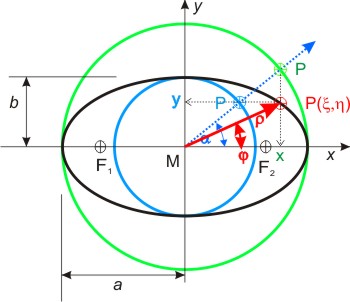 Die Ellipse kann man als gestauchten Kreis ansehen; alle y-Koordinaten der Punkte auf einer Ellipse sind im Verhältnis y : η = b : a verkürzt. Läßt man einen Strahl von Mittelpunkt der Ellipse um den Winkel α laufen, dann kann man die Koordinaten eines Punktes P(ξ,η) auf der Ellipse durch die Koordinaten von Schnittpunkten auf den Inkreis (blau) und dem Umkreis (grün) ausdrücken. Die y-Koordinate η ist identisch mit der y-Koordinate des Punktes auf dem Inkreis (Radius b): η = y = b · sin α.
Die Ellipse kann man als gestauchten Kreis ansehen; alle y-Koordinaten der Punkte auf einer Ellipse sind im Verhältnis y : η = b : a verkürzt. Läßt man einen Strahl von Mittelpunkt der Ellipse um den Winkel α laufen, dann kann man die Koordinaten eines Punktes P(ξ,η) auf der Ellipse durch die Koordinaten von Schnittpunkten auf den Inkreis (blau) und dem Umkreis (grün) ausdrücken. Die y-Koordinate η ist identisch mit der y-Koordinate des Punktes auf dem Inkreis (Radius b): η = y = b · sin α.
Die x-Koordinate des Punktes P(ξ,η) auf der Ellipse ist gleich der x-Koordinate des Punktes auf dem Umkreis (Radius a). Damit lauten die Transformationsgleichungen:
- x = ξ = a · cos α
- y = η = b · sin α
Mit dem Pythagoras erhält man für den Abstand ρ des Ellipsenpunktes vom Mittelpunkt den Ausdruck:
- ρ2 = a2·cos2α + b2·sin2α
Nun brauchen wir noch eine Beziehung zwischen dem Winkel α in dieser Gleichung und dem Polarkoordinatenwinkel φ. Der ist gegeben durch die Definition tan φ = η/ξ = b·sin α / a·cos α. Durch Umformen und Einsetzen bekommt man schließlich die Polargleichung der Ellipse ( mit ε numerische und e lineare Exzentrizität):
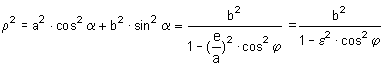
Diese Gleichung beschreibt ebenfalls die Ellipse, nur sind die Koordinaten eines Punktes auf ihr durch den Abstand ρ vom Mittelpunkt und den Winkel φ zwischen ρ und der x-Achse angegeben.
Die Brennpunktgleichung der Ellipse.
In der Schule lernte man zu meiner Zeit außer der Mittelpunktsgleichung noch die Scheitelgleichung der Ellipse. Viel interessanter ist die Brennpunktsgleichung: sie ist die Schlüsselformel für die Vorhersage von Sternenorten. Der Grund hierfür sind das 1. und 2. Keplersche Gesetz: die Erde bewegt sich auf einer Ellipsenbahn um die Sonne, die in einem der beiden Brennpunkte der Bahnellipse steht. Das zweite Keplersche Gesetz ist in der Kepler-Gleichung bereits enthalten.
Kartesiche Koordinaten.
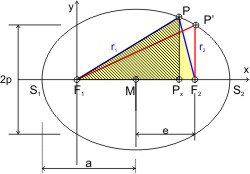 Um die Brennpunktgleichung in karthesischen Koordinaten zu entwickeln, wählt man einen der Brennpunkte als Ursprung des Koordinatensytems. In dem gelben Dreieck ΔF1F2P sind bekannt:
Um die Brennpunktgleichung in karthesischen Koordinaten zu entwickeln, wählt man einen der Brennpunkte als Ursprung des Koordinatensytems. In dem gelben Dreieck ΔF1F2P sind bekannt:
- die Summe der blauen Fahrstrahlen r1 und r2 aus der Definition der Ellipse: r1 + r2 = 2·a (a ist die große Halbachse der Ellipse),
- und
- die Länge der Seite F1F2 = 2 · e (e ist die lineare Exzentrizität).
Der Umfang U des Dreiecks ΔF1F2P ist also konstant für alle Punkte Px, y auf der Ellipse: U = r1 + r2 + 2 · e.
Für den Fall P′x = 2 · e, so ist P′y = p, der Ellipsenparameter. Der Ausdruck für den konstanten Umfang U ergibt sich in diesem Fall zu: U = r1 + p + 2 · e. Und da in diesem Sonderfall das Dreieck ΔF1F2P′ rechtwinklig ist, kann man die Länge von r1 angeben: r12 = p2 + 4 · e2.
Da U eine Konstante für alle Punkte Px, y ist, und nur von den beiden Ellipsenhalbachsen a und b abhängt, kann man mit dem rechtwinkligen, schraffierten Dreieck ΔF1PxP mit der Beziehung zwischen der Hypotenuse r2 und den Katheten eine Gleichung aufstellen, die die Länge des Fahrstrahls r1 mit der y-Koordinate des Punktes P korreliert (ist allerdings etwas aufwändiger). Das Ergebnis ist: r1 + e · y = p.
Eine Formel der Ellipse in karthesischen Koordinaten mit dem Ursprung in einem der Brennpunkte ist nur in der Form der Kepler-Gleichung möglich! — und die ist transzendent und daher nicht lösbar.
Polarkoordinaten.
Hier braucht man die Polargleichung, die als Ursprung den Brennpunkt hat. Die Brennpunktsgleichung in kathesischen Koordinaten ist offensichtlich ungebräuchlich (— jedenfalls habe ich nur einen Hinweis bei Carl Friedrich Gauss gefunden). Die Ableitung erfolgt ähnlich wie bei der Mittelpunktgleichung.
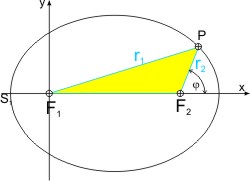 Zum Unterschied ist jedoch das gelbe Dreieck ΔF1F2P schiefwinklig, und wir müssen den Cosinussatz anwenden:
Zum Unterschied ist jedoch das gelbe Dreieck ΔF1F2P schiefwinklig, und wir müssen den Cosinussatz anwenden:
r12 = (2 · r2)² + (2·e)2 - 2 · 2 · e · r2 · cos(180° - φ)
Ausmultiplizieren und Auflösen nach r2 liefert:
Teilt man die rechte Seite durch a, erhält man mit e2/a = ε:
In der Form ähnelt diese Brennpunktgleichung der Mittelpunktgleichung.
Diese polare Brennpunktsgleichung der Ellipse könnte man nun wieder differenzieren und integrieren. Aber die Hauptanwendung ist die Bestimmung des Ortes der Erde auf ihrer Umlaufbahn um die Sonne in Abhängigkeit von der Zeit. Dieses Problem hatte schon Johannes Kepler, und er hat eine Lösung gefunden — ohne Differenzialrechnung (die war noch nicht erfunden, das haben erst 50 Jahre später von Issac Newton und Gottfried Wilhelm Leibnitz entwickelt). Keplers Methode ist hier erklärt.
Die Scheitelgleichung der Ellipse.
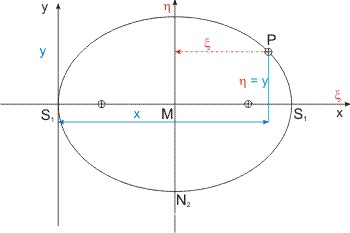 Verlegt man den Ursprung des kartesischen Koordinatensystems vom Mittelpunkt M der Ellipse in einen der Hauptscheitel S1, 2, kann man die "Scheitelgleichung" der Ellipse ableiten. Die Kegelschnitte lassen sich über ihre Scheitelgleichungen vergleichen. Zur Ableitung verwenden wir eine Translation des Ursprungs im Mittelpunktsystem M(ξ η) in das Scheitelsytem S(x, y). Die y-Koordinate ist gleich der η-Koordinate, die ξ-Koordinate wird zu x-Koordinate durch Addition der Strecke MS1 = a (große Halbachse).
Verlegt man den Ursprung des kartesischen Koordinatensystems vom Mittelpunkt M der Ellipse in einen der Hauptscheitel S1, 2, kann man die "Scheitelgleichung" der Ellipse ableiten. Die Kegelschnitte lassen sich über ihre Scheitelgleichungen vergleichen. Zur Ableitung verwenden wir eine Translation des Ursprungs im Mittelpunktsystem M(ξ η) in das Scheitelsytem S(x, y). Die y-Koordinate ist gleich der η-Koordinate, die ξ-Koordinate wird zu x-Koordinate durch Addition der Strecke MS1 = a (große Halbachse).
Aus der Mittelpunktsgleichung oben wird, mit den Koordinaten ξ und η:
![]() durch Einsetzen von ξ = x - a und η = y:
durch Einsetzen von ξ = x - a und η = y:
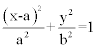 .
.
Nach Auflösen der Gleichung nach y² erhält man:
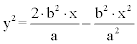 .
.
Jetzt erinnert man sich an den Ellipsenparameter p: p = b² ⁄ a, substituiert ihn in der Formel und erhält: y² = 2·p·x - p·x² ⁄ a, die Scheitelgleichung der Ellipse.
Der Umfang der Ellipse.
Diese polare Mittelpunktsgleichung hat den Vorteil, dass man sie differenzieren kann (zum Formalismus s. a. Loxodrome). Integriert man dann das Differenzial, erhält man entweder die Länge des Ellipsenbogens, oder die Fläche über der Winkeländerung.
Bei der (terrestrischen) Navigation interessiert ausschließlich die Länge des Bogens (also die Entfernung zwischen den Punkten P1(ρ1,α1) und P2(ρ2,α2), die der Winkeländerung Δα entspricht. Dieses Integral hat die Form:
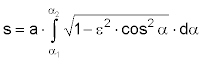
Es ist allerdings nicht analytisch zu lösen (ausser in den Grenzen zwischen 0° und 90°, also für den Viertelbogen). Man muß den Wurzelausdruck in eine konvergierende Reihe entwickeln, und deren Glieder einzeln integrieren. So erhält man für die Bogenlänge der Ellipse die Formel:
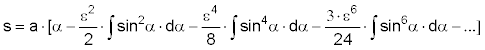
Man sieht, das ist recht aufwändig zu berechnen. Zudem macht man einen Fehler, wenn man die Reihe nach einer endlichen Zahl Glieder abbricht. Integriert man diese Gleichung von 0° bis 360°, erhält man den Umfang der Ellipse.
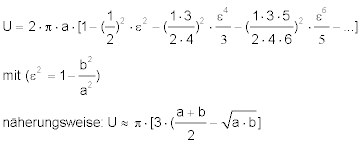
Wie groß ist der Fehler? Berechnen wir die Reihenglieder für den Polumfang des WGS84 Ellipsoids.
| große Halbachse | a = 6.378.137,0 m | a2 = 40.680.631.590.769,0000 |
| kleine Halbachse | b = 6.356.752,3143 m | b2 = 40.408.299.985.358,4000 |
| numerische Exzentrizität | ε = 0,081819190738 | ε2 = 0,006694379973 |
| 1. Glied = 0,001673594993 | 2. Glied = 0,000002100690 | 3. Glied = 0,000000005860 | |
| Umfang | 40.007.947,3383 | 40.007.863,1531 | 40.007.862,9183 |
| Beitrag | 84,1852 | 0,2348 | |
| Näherungsformel | 40.007.862,9174 | ||
| Kreis mit Radius b | 39.940.652,7426 | ||
Wir erkennen, dass das zweite Glied eine Korrektur des Polumfangs von etwa 100 m, das dritte eine von 20 cm beiträgt. Zum Vergleich ergibt die Näherungsformel einen Polumfang, der etwa dem des Reihenabbruchs nach dem ersten Glied entspricht. Der Umfang eines Kreises mit Radius der kleinen Halbachse ist etwa 70 km kürzer als der Ellipsoidumfang (ist ja auch noch ganz ordentlich!).
Ich vermute, das (zivile) GPS arbeitet mit der Näherungsformel, und hat deshalb einen Fehler von (mindestens) 100 m. Das differentielle GPS (DGPS) erlaubt eine weitgehende Korrektur; entsprechend ausgerüstete Geräte haben wohl auch leistungsfähigere Rechner, die bis zum zweiten oder dritten Glied der Reihe rechnen, und so auf Fehler unter 1 m kommen können.
Die Fläche des Ellipsensektors.
Etwas einfacher ist die Fläche des Ellipsensektors zu berechnen. da wir es an anderer Stelle brauchen, soll hier nach dem gleichen Formalismus auch die Fläche des Kreissegmentes berechnet werden.
 Die Fläche des blauen Sektors des Kreises soll berechnet werden. Die Funktion des Kreises lautet:
Die Fläche des blauen Sektors des Kreises soll berechnet werden. Die Funktion des Kreises lautet:
-
 .
.
In differenzierter Form und nach Substitution von x = r · cos φ und dx = r · sin φ:
-

- (Zur Erinnerung: sin2 φ + cos2 φ = 1)
Integrieren mit den Grenzen φ = 0 bis φ ≤ 90° ergibt die Fläche F:
In den Grenzen φ = 0° bis φ = 90° = π ⁄ 2 erhalten wir für ¼ der Kreisfläche:
- F ⁄ 4 = (r2 ⁄ 2) · sin (π ⁄ 2) · cos (π ⁄ 2) + π ⁄ 2 = (r2 ⁄ 2) · (π ⁄ 2);
- F = π · r2.
Die Fläche des gelben Ellipsensektors erhalten wir analog aus der Funktion der Ellipse:
Differenzieren und Substituieren von x = a · cos φ, dx = a · sin φ dφ ergibt:
Integrieren mit den Grenzen φ = 0 bis φ ≤ 90° ergibt die Fläche F:
Die Ellipse bei Apollonius von Perga
Die verschiedenen Parameter der Ellipse versteht man leichter, wenn man ihre Definition aus dem Werk "De Conicis" (Über die Kegelschnitte) von Apollonius von Perga anschaut. Apollonius lebte um 247 v. Chr. (ca. 262 bis ca. 190) und lebte überwiegend in Alexandia und Pergamon. Er verfasste ein acht Bücher über Kegelschnitte, deren Originale verloren sind. Sie lassen sich jedoch rekonstruieren aus den kommentierten Bearbeitungen arabischer (Thebit ben Corah, 830) und persischer (Abalphat von Ispahan (994), Nasireddin von Tus (1259)) Mathematiker. In Europa erkannte Regiomontanus (1436 bis 1476) die Bedeutung der Werke Apollonius und plante eine Übersetzung ins lateinische (zu der es nicht kam). Eine lateinische Ausgabe der ersten vier Bücher der "Conicis" erschien 1566 herausgegeben vom Venetianer Federicus Commandinus Urbinas (im Internet verfügbar) — gerade rechtzeitig für Johannes Keplers Astronomia Nova, der sich mit seiner Ableitung der Ellipsenbahn explizit auf Apollonius bezieht.
Da er in Alexandria mit Schülern des Euklid (um 300 v. Chr.) zusammen kam, bezog sich Apollonius auf dessen Definition im XI. Buch, Definition 18, des Kegels: "Wenn ein rechtwinkliges Dreieck um eine Kathete als Achse gedreht wird, beschreibt die Hypotenuse eine Kegeloberfläche (Mantel des Kegels)." In seinen Büchern zu Kegelschnitten untersucht Apollonius nun die Schnittlinien des Kegelmantels, wenn der durch verschieden geneigte Ebenen geschnitten wird. Er findet und benennt so die Parabel (Lehrsatz 11), die Hyperbel (Lehrsatz 12) und die Ellipse (Lehrsatz 13).
THEOREMA XIII. PROPOSITIO XIII.
Si conus plano per axem secetur, & secetur altero plano conveniente cum utroque latere trianguli per axem, quod neque basi coni æquidistet, neque subcontrarie ponatur; planum autem, in quo est basis coni, & secans planum conveniant secundum rectam lineam, quæ sit perpendicularis vel ad basim trianguli per axem, vel ad eam; quæ directum ipsi constituitur: recta linea, quæ a sectione coni ducitur æquidistans communi sectioni planorum usque ad diametrum sectionis, poterit spatium adiacens lineæ, ad quam sectionis diameter eam proportionem habeat, quam quadratum linea diametro æquidistantis a vertice coni usque ad trianguli basim ducta, habet ad rectangulum contentum basis partibus, quæ inter ipsam & rectas trianguli lineas intericiuntur; latitudinem habens lineam, quæ diametro ab ipsa abscinditur ad verticem sectionis, deficiensque figura simili, & similiter posita ei, quæ diametro, & linea iuxta quam possunt, continetur dicatur autem huiusmodi sectio ellipsis.
Sit conus cuius vertex A punctum, basis circulus BC; & secetur plano per axem, quod sectionem faciat triangulum ABC; secetur autem & altero plano, conveniente cum utroque latere trianguli per axem neque basi coni æquidistante, neque subcontrarie posito, quod faciat sectionem in superficie coni lineam DE; & communis sectio plani secantis, atque eius, in quo est basis coni, sit FG perpendicularis ad BC; diameter autem sectionis ED: & ab E ducatur EH ad ED perpendicularis; perque A ducta AK ipsi ED æquidisiante, fiat ut quadratum AK ad rectangulum BKC, ita DE ad EH; sumatur praeterea in sectione punctum L; & per L ipsi FG æquidistans ducatur LM. Dico LM posse spatium, quod lineæ EH adiacet, latitudinem habens EM, deficiensque figura simili ei, quæ DEH continetur.
Iungatur enim DH; perque M ducatur MXN æquidistans EH: & per H, X puncta ipsi EM æquidistates ducantur HN, XO; postremo per M ducatur PMR æquidistans BC. Itaque quoniam PR æquidistat BC; & LM ipsi FG: erit planum ductum per LM, PR æquidistans plano per FG, BC ducto, hoc est basi coni. si igitur planum per LM, PR producatur: fiet sectio circulus, cuius diameter PR. & est LM ad ipsam perpendicularis, ergo rectangulum BKC. Ita DE a EH: & proportion quadrati AK ad rectangulum BKC componatur ex proportione, quam habet AK ad FKB, & ex ea, quam AK habet ad KC, ut autem AK ad KB, ita EG ad GB, hoc est EM ad MP: & ut AK ad KC, ita DG ad GC, hoc est DM ad MR. erit proportio DE ad EH composita ex proportione EM ad MP, & ex proportione DM ad MR. sed proportio composita ex proportione EM ad MP, & DM ad MR est ea, quam EMD rectangulum habet ad rectangulum PMR.
Quare ut rectangulum EMD ad ipsum PMR, ita DE ad EH, videlicet DM ad MX. ut autem DM ad MX, sumpta ME communi altitudine, ita rectangulum DME ad rectangulum XME. ergo ut DME rectangulum ad rectangulum PMR, ita erit DME rectangulum ad ipsum XME. æquale igitur est rectangulum PMR rectangulo XME. sed rectangulum PMR demonstratum est æquale quadrato LM. quare & ipsum XME quadrato LM æquale erit. linea igitur LM potest spatitum MO: quod quidem linea EH adiacet, latitudinem habens EM, deficiensque figura ON simili ei, quæ DEH continetur. Vocetur autem huius modi sectio ellipsis: & linea EH, iuxta quam possunt, quæ ad diametrum DE ordinatim applicantur; quæ quidem & recta vocabitur ED vero transversa.
EVTOCIVS.
SCIRE oportet hoc theorema tres habere descriptiones, ut sapius dictum est in ellipsi: vel enim DE convenit cum latere AC supra C punctum, vel in ipso C, vel infra cum eo producto convenit.FED. COMMANDINVS.
LINEA igitur LM potest spatium MO: quod quidem lineæ EH adiacet, latitudinem habens EM, deficiensque figura ON simili ei, quæ DEH continetur) Greca verba sunt hac. ἠ ΛΜ ἄρα δύναται τὸ ΜΟ, ὃ παράκειται παρὰ τινὶ θΕ πλάτος ἔχον τινὶ ΕΜ, ἐλλεῖπον εἴδει τῷ ΟΝ ὁμοίῳ ὄντι τῷὑπὸ ΔΕθ. Ex quibus manifeste constat, cur ea sectio ellipsis appelata sit.
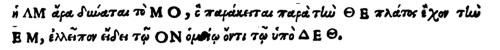 Transscription mit freundlicher Hilfe von Walther Frederking — der außer Latein auch Griechisch kann.
Transscription mit freundlicher Hilfe von Walther Frederking — der außer Latein auch Griechisch kann.
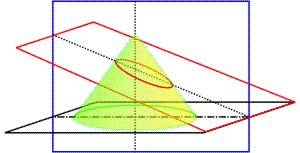 Wenn ein (gerader Kreis-) Kegel durch eine Ebene, in der die Kegelachse liegt, geschnitten wird, die nicht parallel (eigentlich: gleiche Entfernung hat) zur Basis liegt, und mit den beiden Schenkeln des durch die erste Schnittebene gebildeten Dreiecks zusammentrifft, und die nicht den gegenständigen Teil des Doppelkegels berührt, die Ebene aber, in der die Basis des Kegels liegt, in einer geraden Linie schneidet, die senkrecht steht sowohl auf der Basis(linie) des Dreiecks durch die Achse, als auch auf der schneidenden Ebene; diese gibt die Richtung vor: einer senkrechten Linie, die vom Kegelschnitt parallel zur gemeinsamen Schnittlinie in der Schnittebene bis zum Durchmesser des Schnitts gezogen wird, diese wird eine Länge haben, zu der der Durchmesser des Schnitts das gleiche Verhältnis hat wie das Quadrat einer Linie, die parallel zur Schnittebene von der Kegelspitze bis zu einem Schnittpunkt mit der verlängerten Basis des Dreiecks gezogen wird, zum Rechteck aus der (verlängerten) Basis und dem Abschnitt der zwischen den Dreieckseiten liegt; als Breite habe es [das Rechteck] eine Linie die vom Durchmesser abgeschnitten wird am Scheitel des Schnitts, und dem Rechteck fehlt ein Rechteck, das gleich ist und gleich dem gelegt sein kann, das vom Durchmesser und der verbundenen Linie, der so entstandene Kegelschnitt wird Ellipse genannt.
Wenn ein (gerader Kreis-) Kegel durch eine Ebene, in der die Kegelachse liegt, geschnitten wird, die nicht parallel (eigentlich: gleiche Entfernung hat) zur Basis liegt, und mit den beiden Schenkeln des durch die erste Schnittebene gebildeten Dreiecks zusammentrifft, und die nicht den gegenständigen Teil des Doppelkegels berührt, die Ebene aber, in der die Basis des Kegels liegt, in einer geraden Linie schneidet, die senkrecht steht sowohl auf der Basis(linie) des Dreiecks durch die Achse, als auch auf der schneidenden Ebene; diese gibt die Richtung vor: einer senkrechten Linie, die vom Kegelschnitt parallel zur gemeinsamen Schnittlinie in der Schnittebene bis zum Durchmesser des Schnitts gezogen wird, diese wird eine Länge haben, zu der der Durchmesser des Schnitts das gleiche Verhältnis hat wie das Quadrat einer Linie, die parallel zur Schnittebene von der Kegelspitze bis zu einem Schnittpunkt mit der verlängerten Basis des Dreiecks gezogen wird, zum Rechteck aus der (verlängerten) Basis und dem Abschnitt der zwischen den Dreieckseiten liegt; als Breite habe es [das Rechteck] eine Linie die vom Durchmesser abgeschnitten wird am Scheitel des Schnitts, und dem Rechteck fehlt ein Rechteck, das gleich ist und gleich dem gelegt sein kann, das vom Durchmesser und der verbundenen Linie, der so entstandene Kegelschnitt wird Ellipse genannt.
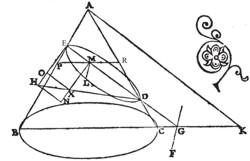
Sei ein Kegel gegeben, dessen Spitze der Punkt A ist, mit einer kreisförmigen Basis BC; und werde er durch eine Ebene durch die Achse geschnitten, welcher Schnitt das Dreieck ABC erzeugt; und werde er außerdem durch eine andere Ebene geschnitten, die beide Seiten des Dreiecks durch die Achse treffen und weder zur Kegelbasis parallel sind, noch mit dem Gegenkegel zusammentrifft, was in der Kegeloberfläche eine Schnittline DE erzeuge; und der gemeinsame Schnitt der Ebene des Kegelschnitts mit der, in der die Basis des Kegels liegt, sei FG senkrecht zu BC; der Durchmesser des Kegelschnitts sei jetzt ED: und in E wird EH senkrecht zu ED gezogen; und AK von A parallel ED gezogen, so dass wie das Quadrat AK zum Rechteck BKC [sich verhält], so DE sich zu EH [verhält]; außerdem wird auf dem Kegelschnitt ein Punkt L hinzugefügt; und von L die Strecke LM parallel zu FG gezogen. Ich behaupte LM hat eine Länge …
Erläuterungen
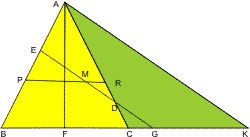 In der Ebene durch die Kegelachse bilden die beiden Schnittlinien des Kegelmantels AB und AC ein gleichseitiges Dreieck ABC (gelb), und die zur Kegelschnittebene EG parallele Linie AK ein stumpfwinkliges Dreieck ACK (grün).
In der Ebene durch die Kegelachse bilden die beiden Schnittlinien des Kegelmantels AB und AC ein gleichseitiges Dreieck ABC (gelb), und die zur Kegelschnittebene EG parallele Linie AK ein stumpfwinkliges Dreieck ACK (grün).
Durch die Konstruktion mit den parallelen Strecken EG und AK, die die Schenkel eines Winkels ∠ABK schneiden, entstehen zwei ähnliche Dreiecke ABK und EBG. Es gilt für die Abschnitte auf den Schenkeln des Winkel ∠ABK: AB : BE = BK : BG. Also zusammengefaßt findet man die Verhältnisse
AK : EG = BK : BG = AB : BE.
Und die Strecke AK kann man mit dem Lehrsatz 12 aus dem zweiten Buch des Euklid mit der Kegelbasis ins Verhältnis setzen. In dem stumpfwinkliges Dreieck ACK gilt:
"In einem stumpfwinkligen Dreieck, ist das Quadrat der Seite, die dem stumpfen Winkel gegenüber liegt, größer als die Summe der Quadrate der beiden Seiten, die den stumpfen Winkel einschließen, und zwar um das doppelte Rechteck aus einer der beiden Seiten und dem Abstand von der Dreiecksecke zum Fußpunkt F der Höhe AF."
Also:
AK2 = AC2 + CK2 + 2 · CF · CK = AC2 + CK2 + BC · CK
(weil beim geraden Kreiskegel die Kegelachse jeden Durchmesser des Basiskreise halbiert:
2 · CF = BC)
Es verhalten sich auch die Abschnitte auf den Schenkeln des Winkels ∠ABK, der durch die beiden Parallelen AK und EG geschnitten wird:
AB : BE = AK : EG
BK : BG = AK : EG
© Rainer Stumpe, URL: www.rainerstumpe.de/
Datenschutzerklärung